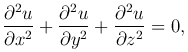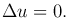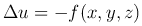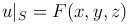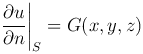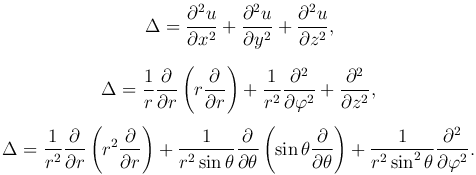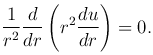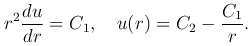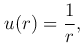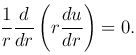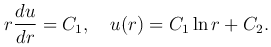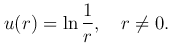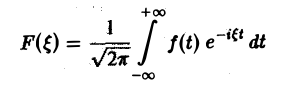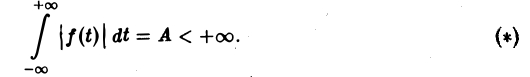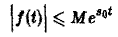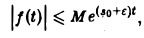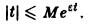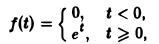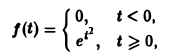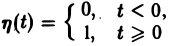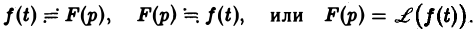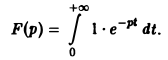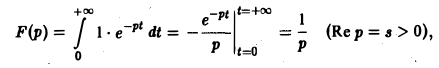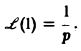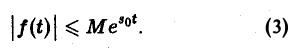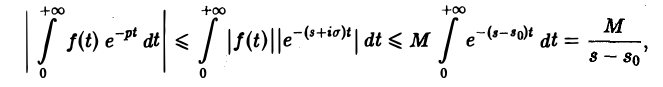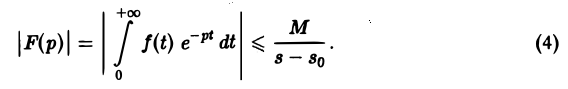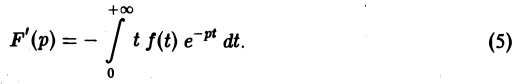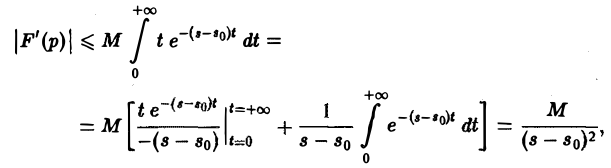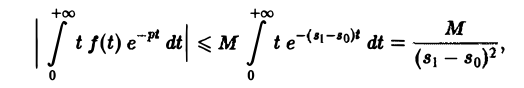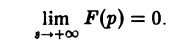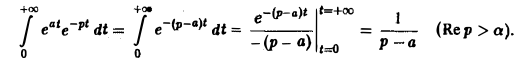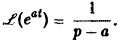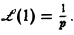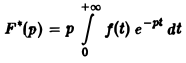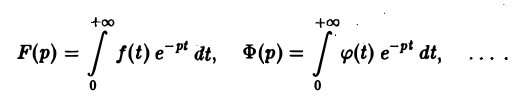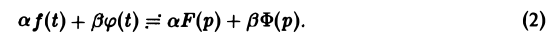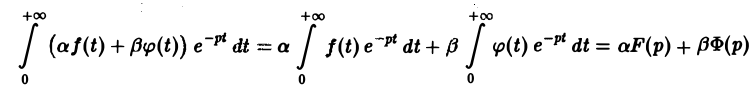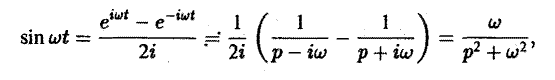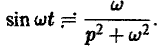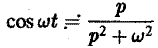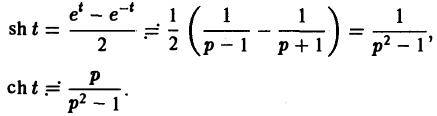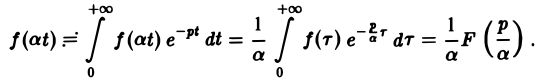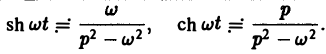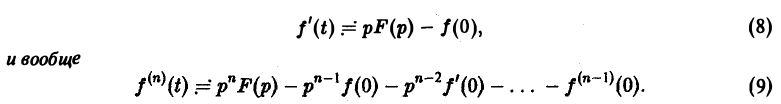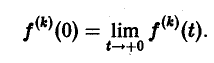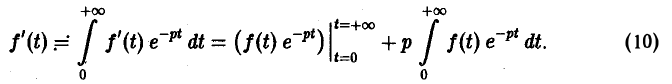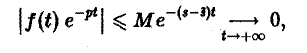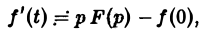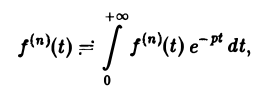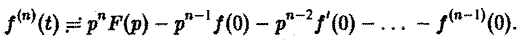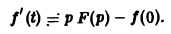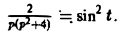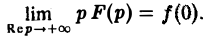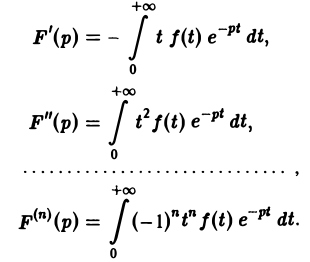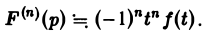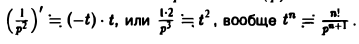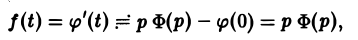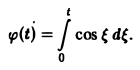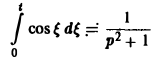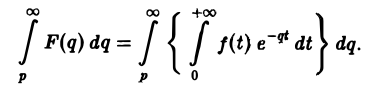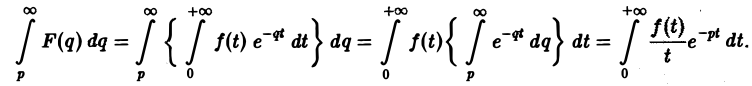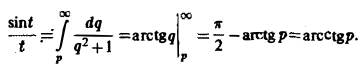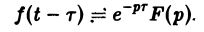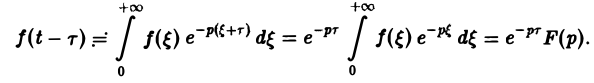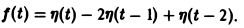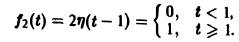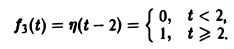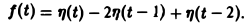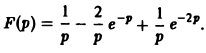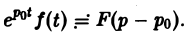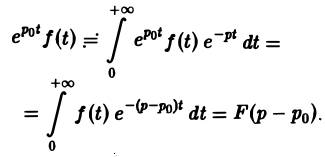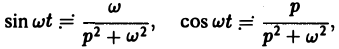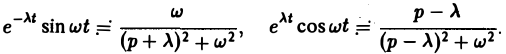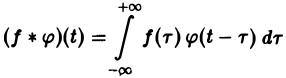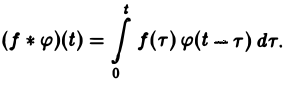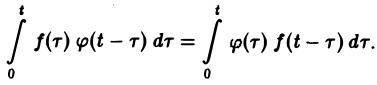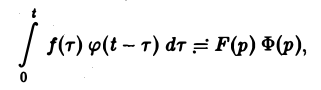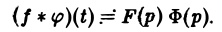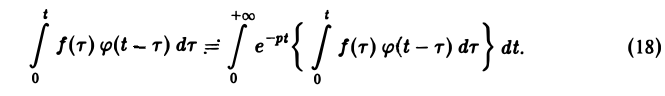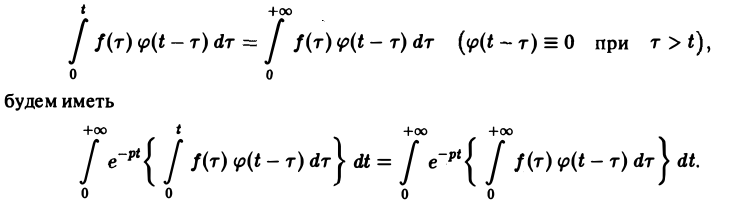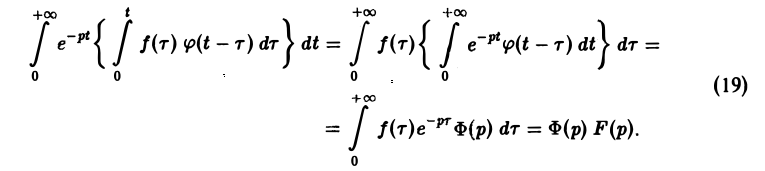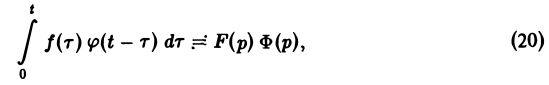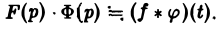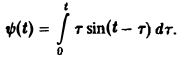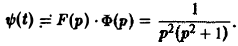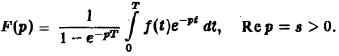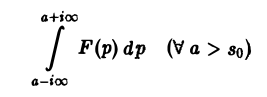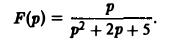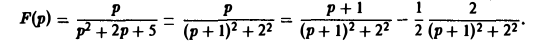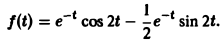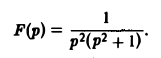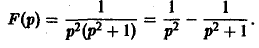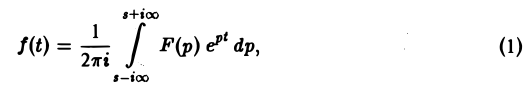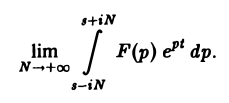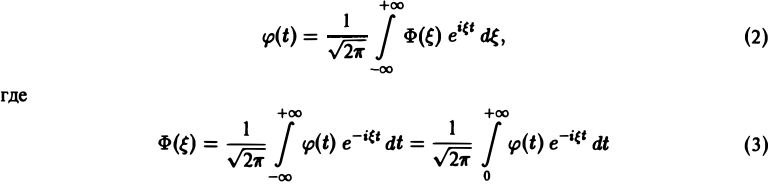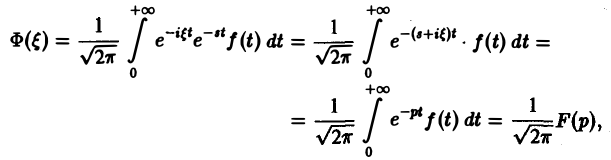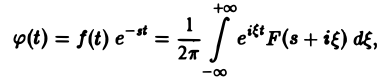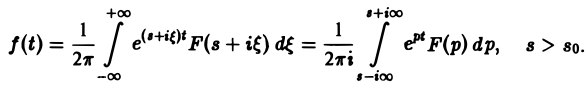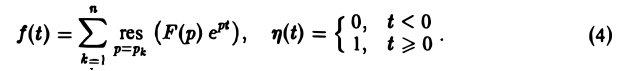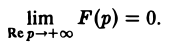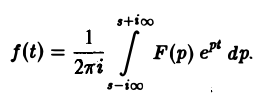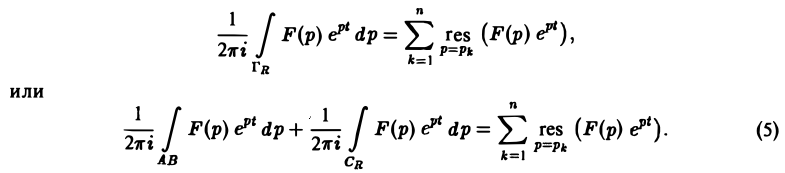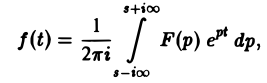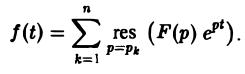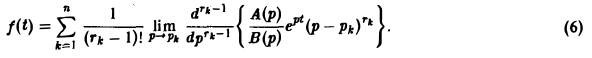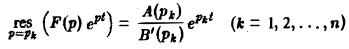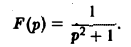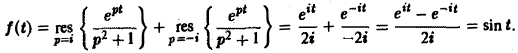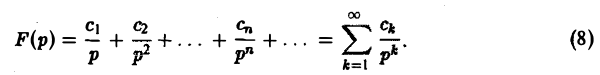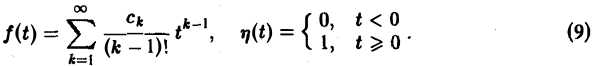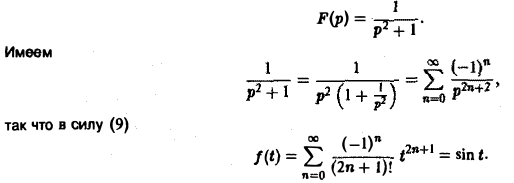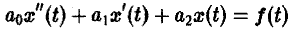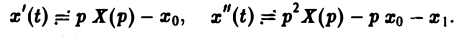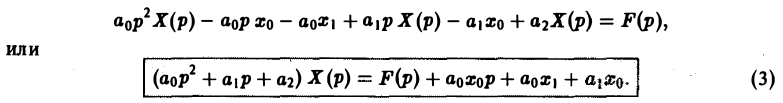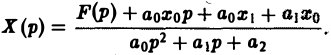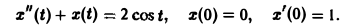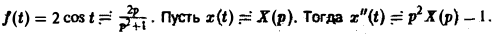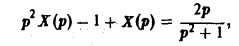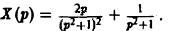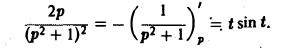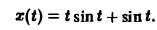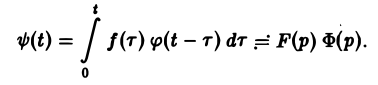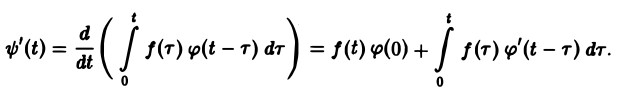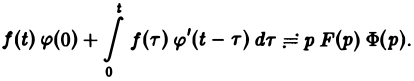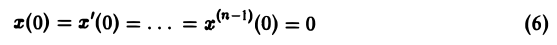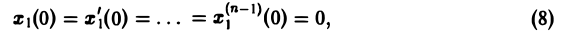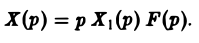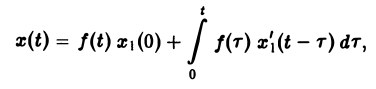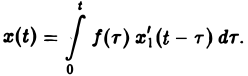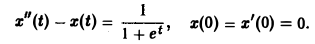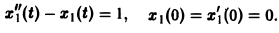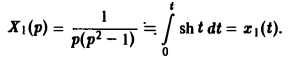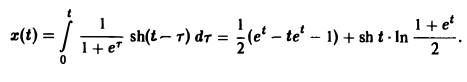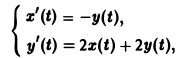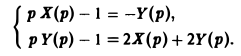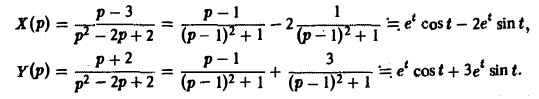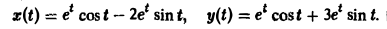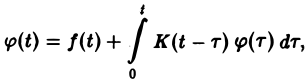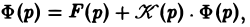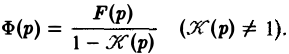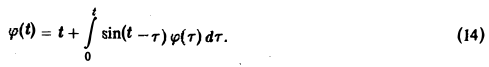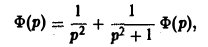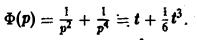Фундаментальное решение уравнения лапласа в трехмерном случае

Видео:Уравнения математической физики. Уравнение Лапласа. Часть 1Скачать

Уравнение Лапласа

Рассмотрим уравнение с частными производными вида

где u=u(x, y, z). Это уравнение называется уравнением Лапласа.

Левая часть обозначается Δu и называется оператором Лапласа. Таким образом, это уравнение преобразуется к виду:

Данному уравнению удовлетворяет потенциал скорости безвихревого течения несжимаемой (с постоянной плотностью) жидкости; потенциал сил тяготения или сил взаимодействия электрических зарядов во всех точках пространства, находящихся вне притягивающих масс или вне зарядов, создающих поле; температура в однородном теле, если теплообмен является стационарным, т.е. температура u зависит только от места, но не от времени и др.

называется уравнением Пуассона.

Уравнение Лапласа и уравнение Пуассона является уравнениями эллиптического типа.

Определение. Функцию, непрерывную в некоторой области вместе со своими частными производными до второго порядка включительно и удовлетворяющую уравнению Лапласа, называют гармонической.

Обычно в задачах, связанных с уравнением Лапласа или Пуассона, искомое решение должно удовлетворять уравнению в области D, а также некоторому дополнительному условию на границе S области D.

Если надо определить функцию, гармоническую в области D, когда на границе S области D заданы ее значения, т.е.

(первая краевая задача), то такая задача называется задачей Дирихле.

Если же надо определить функцию, гармоническую в области D, когда на границе S задается значение нормальной производной

(вторая краевая задача), то такая задача называется задачей Неймана.

Определение. Если решение задачи ищут в области D, внутренней (внешней) по отношению к поверхности S, то соответствующую задачу называют внутренней (внешней) краевой задачей.

Видео:7.1 Решение уравнения Лапласа в прямоугольникеСкачать

Фундаментальные решения уравнения Лапласа

Рассмотрим уравнение Лапласа

где оператор Лапласа в декартовой, цилиндрической и сферической системах координат определяется соответственно

Важную роль при решении задач для уравненийй Лапласа и Пуассона представляют решения, обладающие сферической или цилиндрической симметрией.

Найдем решение уравнения Лапласа, удовлетворяющее условию сферической симметрии, когда функция u зависит только от расстояния 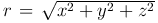точки M(x, y, z) до начала координат. В этом случае уравнение Лапласа в сферической системе координат имеет вид

Интегрируя это уравнение, получим

которая удовлетворяет уравнению Лапласа всюду, кроме точки r=0, где она обращается в бесконечность. Такую функцию называют фундаментальным решением уравнения Лапласа в пространстве.

В задаче с осевой симметрией, когда функция u в цилиндрической системы координат не зависит от φ и z, уравнение Лапласа имеет вид

Интегрируя это уравнение, получим

Эта функция называется фундаментальным решением уравнения Лапласа на плоскости.

Видео:Радкевич Е.В. - Уравнения математической физики - 4.Фундаментальное решение уравнения ЛапласаСкачать

Преобразование Лапласа с примерами решения и образцами выполнения

Ранее мы рассмотрели интегральное преобразование Фурье

с ядром K(t, ξ) = .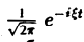

Преобразование Фурье неудобно тем, что должно быть выполнено условие абсолютной интегрируемости функции f(t) на всей оси t,

Преобразование Лапласа позволяет освободиться от этого ограничения.

Определение:

Функцией-оригиналом будем называть всякую комплекснозначную функцию f(t) действительного аргумента t, удовлетворяющую следующим условиям:

1. f(t) непрерывна на всей оси t, кроме отдельных точек, в которых f(t) имеет разрыв 1-го рода, причем на каждом конечном интервале оси t таких точек может быть лишь конечное число;
2. функция f(t) равна нулю при отрицательных значениях t, f(t) = 0 при t 0 и з такие, что для всех t

Ясно, что если неравенство (1) выполняется при некотором s = s1, то оно будет выполнятся при всяком s2 > s1.

Точная нижняя грань sо всех чисел s, so = infs, для которых выполняется неравенство (1), называется показателем роста функции f(t).

Замечание:

В общем случае неравенство

не имеет места, но справедлива оценка

где ε > 0 — любое. Так, функция f(t) = t, t ≥ 0, имеет показатель роста so =0. Для нее неравенство |t| ≤ М ∀t ≥ 0 не выполняется, но ∀ε > О, ∀t > 0 верно неравенство

Условие (1) гораздо менее ограничительное, чем условие (*).

Пример:

не удовлетворяет условию (*), но условие (1) выполнено при любом s ≥ 1 и М ≥ 1; показатель роста so = 1. Так что f(t) является функцией-оригиналом. С другой стороны, функция

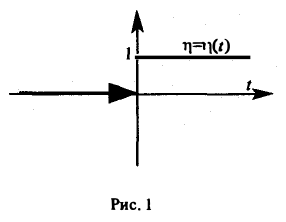
не является функцией-оригиналом: она имеет бесконечный порядок роста, sо = +∞. Простейшей функцией-оригиналом является
так называемая единичная функция

Если некоторая функция φ(t) удовлетворяет условиям 1 и 3 определения 1, но не удовлетворяет условию 2, то произведение f(t) = φ(t) η(t) уже является функцией-оригиналом.

Для простоты записи мы будем, как правило, множитель η(t) опускать, условившись, что все функции, которые мы будем рассматривать, равны нулю для отрицательных t, так что если речь идет о какой-то функции f(t) например, о sin t, cos t, e t и т. д., то всегда подразумеваются следующие функции (рис. 2):

Определение:

Пусть f(t) есть функция-оригинал. Изображением функции f(t) по Лапласу называется функция F(p) комплексного переменного р = s + iσ, определяемая формулой

где интеграл берется по положительной полуоси t. Функцию F(p) называют также преобразованием Лапласа функции f(t); ядро преобразования K(t, р) = e -pt .
Тот факт, что функция f(x) имеет своим изображением F(p), будем записывать так:

Пример:

Найти изображение единичной функции η(t).

Функция 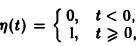является функцией-оригиналом с показателем роста s0 = 0. В силу формулы (2) изображением функции η(t) будет функция

Если р = s + iσ, то при s > 0 интеграл в правой части последнего равенства будет сходящимся, и мы получим

так что изображением функции η(t) будет функция 1/p. Как мы условились, будем писать, что η(t) = 1, и тогда полученный результат запишется так:

Теорема:

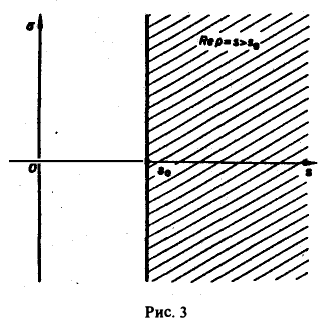
Для всякой функции-оригинала f(t) с показателем роста sо изображение F(p) определено в полуплоскости Re p = s > So и является в этой полуплоскости аналитической функцией (рис. 3).

Для доказательства существования изображения F(p) в указанной полуплоскости достаточно установить, что несобственный интеграл (2) абсолютно сходится при s > so. Используя (3), получаем

что и доказывает абсолютную сходимость интеграла (2). Одновременно мы получили оценку преобразования Лапласа F(p) в полуплоскости сходимости Re р = s > so

Дифференцируя выражение (2) формально под знаком интеграла по р, находим

Существование интеграла (5) устанавливается так же, как было установлено существование интеграла (2).

Применяя для F'(p) интегрирование по частям, получаем оценку

откуда следует абсолютная сходимость интеграла (5). (Внеинтегральное слагаемое 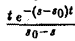— при t → + ∞ имеет предел, равный нулю). В любой полуплоскости Re р ≥ S1 > So интеграл (5) сходится равномерно относительно р, поскольку он мажорируется сходящимся интегралом

не зависящим от р. Следовательно, дифференцированиепо р законно и равенство (5) справедливо.

Поскольку производная F'(p) существует, преобразование Лапласа F(p) всюду в полуплоскости Re p = s > sо является аналитической функцией.

Из неравенства (4) вытекает

Следствие:

Если точка р стремится к бесконечности так, что Re р = s неограниченно возрастает, то

Пример:

Найдем еще изображение функции f(t) =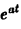, где а = а + iβ — любое комплексное число.

Показатель роста sо функции f(t) равен а.

Считая Rep = s> а, получим

При а = 0 вновь получаем формулу

Обратим внимание на то, что изображение функции 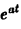является аналитической функцией аргумента р не только в полуплоскости Re p > а, но и во всех точках р, кроме точки р = а, где это изображение имеет простой полюс. В дальнейшем мы не раз встретимся с подобной ситуацией, когда изображение F(p) будет аналитической функцией во всей плоскости комплексного переменного р, за исключением изолированных особых точек. Противоречия с теоремой 1 нет. Последняя утверждает лишь, что в полуплоскости Re p > So функция F(p) не имеет особых точек: все они оказываются лежащими или левее прямой Re p = So, или на самой этой прямой.

Замечание:

В операционном исчислении иногда пользуются изображением функции f(t) по Хевисайду, определяемым равенством

и отличаюикмся от шоСражения по Лапласу множителем р.

Видео:Решение уравнения Лапласа в шареСкачать

Свойства преобразования Лапласа

В дальнейшем через f(t), φ(t), … будем обозначать функции-оригиналы, а через F(p), Ф(р), … — их изображения по Лапласу,

Из определения изображения следует, что если f(t) = 9 ∀t, то F(p) = 0.

Теорема единственности:

Теорема:

Справедливость утверждения вытекает из свойства линейности интеграла, определяющего изображение:

— показатели роста функций f(t) и φ(t) соответственно).

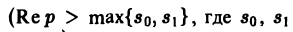
На основании этого свойства получаем

Аналогично находим, что
(4)

Теорема подобия:

Если f(t) — функция-оригинал и F(p) — ее изображение по Лапласу, то для любого постоянного а > 0

Полагая at = т, имеем

Пользуясь этой теоремой, из формул (5) и (6) получаем

Теорема:

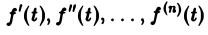
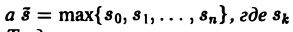
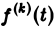
О дифференцировании оригинала. Пусть f(t) является функцией-оригиналом с изображением F(p) и пусть — также функции-оригиналы, — показатель роста функции (k = 0, 1,…, п). Тогда

Здесь под fk(0) (k = 0,1,… , п — 1) понимается правое предельное значение .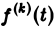

Пусть f(t) = F(p). Найдем изображение f'(t). Имеем

Интегрируя по частям, получаем

Внеинтегральное слагаемое в правой части (10) обращается в нуль при t → + ∞, т. к. при Re р = s > 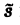имеем

подстановка t = 0 дает -f(0).

Второе слагаемое справа в (10) равно pF(p). Таким образом, соотношение (10) принимаетвид

и формула (8) доказана. В частности, если f(0) = 0, то f'(t) = pF(p). Для отыскания изображения 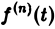запишем

откуда, интегрируя п раз по частям, получим

Пример:

Пользуясь теоремой о дифференцировании оригинала, найти изображение функции f(t) = sin 2 t.

Пусть f(t) = F(p). Тогда

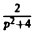
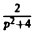
Но f(0) = О, а f'(0) = 2 sin t cos t = sin 2t = . Следовательно, = pF(p), откуда F(p) =

Теорема 5 устанавливает замечательное свойство интегрального преобразования Лапласа: оно (как и преобразование Фурье) переводит операцию дифференцирования в алгебраическую операцию умножения на р.

Формула включения. Если f(t) и f'(t) являются функциями-оригиналами, то (11)

В самом деле, f'(

Так как функция F(p) в полуплоскости Rep = s > so является аналитической, то ее можно дифференцировать по р. Имеем

Последнее как раз и означает, что

Пример:

Пользуясь теоремой 6, найти изображение функции .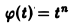

Как известно, 1 = 1/p. Здесь f(t) = 1, F(p) = 1/p. Отсюда (1/p)’= (-t) • 1, или 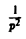= t. Вновь применяя теорему 6, найдем

Теорема:

Интегрирование оригинала. Интегрирование оригинала сводится к делению изображения на р: если f(t) = F(p), то

Нетрудно проверить, что если f(t) есть функция-оригинал, то и φ(t) будет функцией-оригиналом, причем φ(0) = 0. Пусть φ(t) = Ф(р). В силу (14)

С другой стороны, f(t) =’ F(p), откуда F(p) = рФ(р), т.е. Ф(р) =.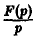

Последнее равносильно доказываемому соотношению (13).

Пример:

Найти изображение функции

В данном случае f(t) = cos t, так что F(p) = 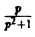. Поэтому

Теорема:

Интегрирование изображения. Если f(t) = F(p) и интеграл 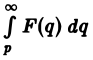сходится, то он служит изображением функции

Предполагая, что путь интегрирования (р, ∞) лежит в полуплоскости Re p ≥ а> so, мы можем изменить порядок интегрирования (t > 0):

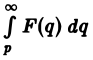
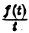
Последнее равенство означает, что является изображением функции .

Пример:

Найти изображение функции .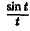

Как известно, sin t = .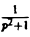

Теорема запаздывания:

Положим ξ = t- τ. Тогда dt = d ξ. При t = τ получаем ξ = 0, при t = + ∞ имеем ξ = + ∞.

Поэтому соотношение (16) принимает вид

Пример:

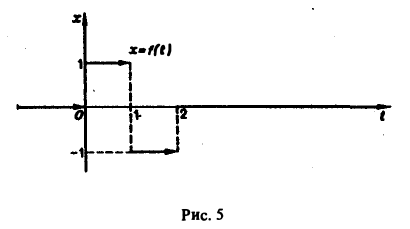
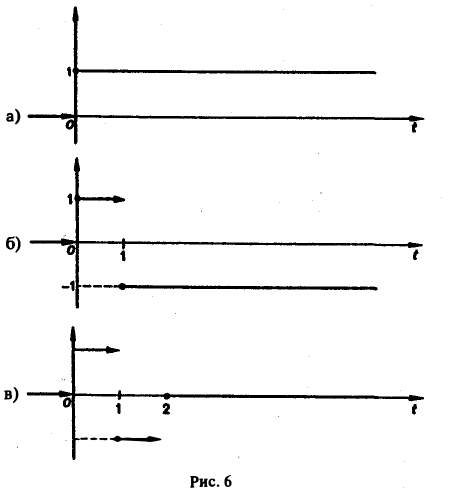
Найти изображение функции f(t), заданной графически (рис. 5).

Запишем выражение для функции f(t) в следующем виде:

Это выражение можно получить так. Рассмотрим функцию f1(t) = η(t) для t ≥ 0 (рис. 6 а) и вычтем из нее функцию

Разность f(t) — h(t) будет равна единице для t ∈ [0,1) и -1 для t ≥ 1 (рис. 6 b). К полученной разности прибавим функцию

В результате получим функцию f(t) (рис. 6 в), так что

Отсюда, пользуясь теоремой запаздывания, найдем

Теорема смещения:

Теорема позволяет по известным изображениям функций находить изображения тех же функций, умноженных на показательную функцию 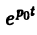, например,

Свертка функций. Теорема умножения

Пусть функции f(t) и φ(t) определены и непрерывны для всех t. Сверткой (f *φ)(t) этих функций называется новая функция от t, определяемая равенством

(если этот интеграл существует).

Для функций-оригиналов f(t) и φ(t) операция свертки всегда выполнима, причем
(17)

В самом деле, произведение функций-оригиналов f( τ ) φ(t — τ), как функция от τ, является финитной функцией, т.е. обращается в нуль вне некоторого конечного промежутка (в данном случае вне отрезка 0 ≤ τ ≤ t). Для финитных непрерывных функций операция свертки выполнима, и мы получаем формулу (17).

Нетрудно проверить, что операциясвертки коммутативна,

Теорема умножения:

Нетрудно проверить, что свертка (f * φ)(t) функций-оригиналов есть функция-оригинал с показателем роста s* = mах, где s1, s2

показатели роста функций f(t) и φ(t) соответственно. Найдем изображение свертки,

Воспользовавшись тем, что

Меняя порядок интегрирования в интеграле справа (при Re р = s > s* такая операция законна) и применяя теорему запаздывания, получим

Таким образом, из (18) и (19) находим

— умножению изображений отвечает свертывание оригиналов,

Пример:

Найти изображение функции

Функция ψ(t) есть свертка функций f(y) = t и φ(t) = sin t. В силу теоремы умножения

Задача:

Пусть функция f(t), периодическая с периодом Т, есть функция-оригинал. Показать, что ее изображение по Лапласу F[p) дается формулой

Видео:Формулы ГринаСкачать

Отыскание оригинала по изображению

Задача ставится так: дана функция F(p), надо найти функцию f(t). изображением которой является F(p).

Сформулируем условия, достаточные для того, чтобы функция F(p) комплексного переменного р служила изображением.

Теорема:

Если аналитическая в полуплоскости Rep = s > so функция F(p)

1) стремится к нулю при |р| —» + ∞ в любой полуплоскости Re р = а > So равномерно относительно arg р;

сходится абсолютно, то F(p) является изображением некоторой функции-оригинала f<t).

Задача:

Может ли функция F(p) = 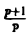служить изображением некоторой функции-оригинала? Укажем некоторые способы отыскания оригинала по изображению.

Отыскание оригинала с помощью таблиц изображений

Прежде всего стоит привести функцию F(p) к более простому, «табличному» виду. Например, в случае, когда F(p) — дробно-рациональная функция аргумента р,ее разлагают на элементарные дроби и пользуются подходящими свойствами преобразования Лапласа.

Пример:

Найти оригинал для

Запишем функцию F(p) в виде:

Пользуясь теоремой смещения и свойством линейности преобразования Лапласа, получаем

Пример:

Найти оригинал для функции

Запишем F(p) в виде

Отсюда f(t) = t — sin t.

Использование теоремы обращения и следствий из нее

Теорема обращения:

где интеграл берется вдоль любой прямой Re p = s > So и понимается в смысле главного значения, т. е. как

Формула (1) называется формулой обращения преобразования Лапласа, или формулой Меллина. В самом деле, пусть, например, f(t) — кусочно-гладкая на каждом конечном отрезке [0, а] функция-оригинал-с показателем роста so. Рассмотрим функцию φ(t) = 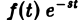, где s>so — любое.

Функция φ(t) удовлетворяет условиям применимости интегральной формулы Фурье, и, следовательно, справедлива формула обращения преобразования Фурье,

(φ(t) ≡ 0 при t

откуда получаем формулу обращения преобразования Лапласа

Как следствие из теоремы обращения получаем теорему единственности.

Теорема:

Две непрерывные функции f(t) и φ(t), имеющие одно и то же изображение F(p), тождественны.
Непосредственное вычисление интеграла обращения (1) обычно затруднительно. Отыскание оригинала по изображению упрощается при некоторых дополнительных ограничениях на F(p).

Теорема:

Пусть изображение F(p) — дробно-рациональная функция с полюсами р1, p2….pп. Тогда оригиналом для F(p) будет функция f(t) η(t), где

Пусть изображение F(p) — дробно-рациональная функция, F(p) = 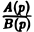, где А(р), В(р) — многочлены относительно р (взаимно простые), причем степень числителя А(р) меньше степени знаменателя В(р), т. к. для всякого изображения должно выполняться предельное соотношение

Пусть корни знаменателя В(р), являющиеся полюсами изображения F(p), суть р1, р2, …, рп, а их кратности равны r1, r2, …, rп соответственно.

Если число s, фигурирующее в формуле (1), взять большим всех Re pk (k = 1,2,…, п), то по формуле обращения, которая в этих условиях применима, получим

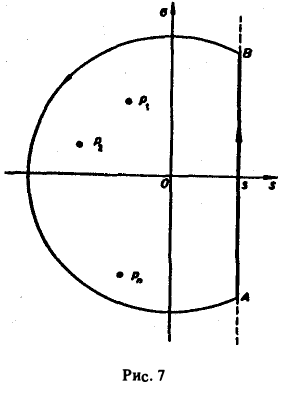
Рассмотрим замкнутый контур ГR (рис.7), состоящий из дуги CR окружности радиуса R с центром в начале координат и стягивающей ее хорды АВ (отрезка прямой Re р = s), и проходимый в положительном направлении, причем радиус R настолько велик, что все полюсы F(p) лежат внутри ГR.

По теореме Коши о вычетах при любом R, удовлетворяющем указанному условию, будем иметь

Второе слагаемое слева в равенстве (5) стремится к нулю при R → ∞. Это следует из леммы Жордана, если в ней заменить р на iz и учесть, что F(p) → 0 при Re p → + ∞. Переходя в равенстве (5) к пределу при R → ∞, мы получим слева

а справа — сумму вычетов по всем полюсам функции F(p)

Замечание:

Воспользовавшись формулой для вычисления вычетов, найдем, что

Если все полюсы p1, р2,…, рn — простые, то

и формула (6) принимает вид

Пример:

Найти оригинал для функции

Функция F(p) имеет простые полюсы р1 = i. p2 = -i. Пользуясь формулой (7), находим

Теорема:

Пусть изображение F(p) является аналитической функцией в бесконечно удаленной точке р = ∞, причем ее разложение в окрестности |р| > R бесконечно удаленной точки имеет вид

Тогда оригиналом для F(p) будет функция f(t) η<t), где

Пример:

Видео:Горицкий А. Ю. - Уравнения математической физики. Часть 2 -Фундаментальное решение оператора ЛапласаСкачать

Приложения преобразования Лапласа (операционного исчисления)

Решение линейных дифференциальных уравнений с постоянными коэффициентами

Дано линейное дифференциальное уравнение второго порядка с постоянными коэффициентами
(1)

(ао, а1, а2 — действительные числа) и требуется найти решение уравнения (1) для t > 0, удовлетворяющее начальным условиям

Будем считать, что f(t) есть функция-оригинал. Тогда x(t) — также функция-оригинал. Пусть

f(t) = F(p), x(t) = X(p).

По теореме о дифференцировании оригинала имеем

Перейдем в уравнении (1) от оригиналов к изображениям. Имеем

Это уже не дифференциальное, а алгебраическое уравнение относительно изображения Х(р) искомой функции. Его называют операторным уравнением. Решая его, найдем операторное решение задачи (1)-(2) —

Оригинал для Х(р) будет искомым решением х(t) задачи (1)-(2).

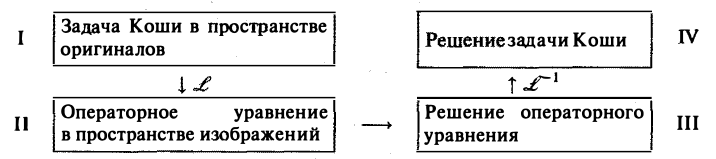
Общий случай линейного дифференциального уравнения n-го порядка (n ≥ 1) с постоянными коэффициентами от случая п = 2 принципиально ничем не отличается.

Приведем общую схему решения задачи Коши

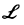
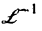
Здесь означает применение к 1 преобразование Лапласа, — применение к III обратного преобразования Лапласа.

Пример:

Решить задачу Коши

По теореме о дифференцировании изображения

Формула Дюамеля

В приложениях операционного исчисления к решению дифференциальных уравнений часто пользуются следствием из теоремы умножения, известным под названием формулы Дюамеля.

Пусть f(t) и φt) — функции-оригиналы, причем функция f(t) непрерывна на [0, + ∞), a φ(t) — непрерывно дифференцируема на [0,+ ∞). Тогда если f(t) = F(p), φ<t) = Ф(р),то по теореме умножения получаем, что

Нетрудно проверить, что функция ψ(t) непрерывно дифференцируема на [0, + ∞), причем

Отсюда, в силу правила дифференцирования оригиналов, учитывая, что ψ(0) = 0, получаем формулу Дюамеля
(4)

Покажем применение этой формулы.

Пусть требуется решить линейное дифференциальное уравнение n-го порядка (n ≥ 1) с постоянными коэффициентами

при нулевых начальных условиях

(последнее ограничение несущественно: задачу с ненулевыми начальными условиями можно свести к задаче с нулевыми условиями заменой искомой функции).

Если известно решение x(t) дифференциального уравнения с той же левой частью и правой частью, равной единице,

L[x(t)] = l (7)

при нулевых начальных условиях

то формула Дюамеля (4) позволяет сразу получить решение исходной задачи (5)-(6).

В самом деле, операторные уравнения, отвечающие задачам (5)-(6) и (7)-(8), имеют соответственно вид

где F(p) — изображение функции f(t). Из (9) и (10) легко находи

Отсюда по формуле Дюамеля

или, поскольку x1(0) = 0, (11)

Пример:

Решить задачу Коши

Рассмотрим вспомогательную задачу

Применяя операционный метод, находим

По формуле (11) получаем решение x(t) исходной задачи:

Интегрирование систем линейных дифференциальных уравнений с постоянными коэффициентами

Интегрирование систем осуществляется так же, как и решение одного линейного дифференциального уравнения — путем перехода от системы дифференциальных уравнений к системе операторных уравнений. Решая последнюю как систему линейных алгебраических уравнений относительно изображений искомых функций, получаем операторное решение системы. Оригинал для негобудетрешением исходной системы дифференциальных уравнений.

Пример:

Найти решение линейной системы

удовлетворяющее начальным условиям х(0) = у(0) = I.

Пусть х(

Решая последнюю относительно Х(р) и У(р), получаем

Решение исходной задачи Коши

Решение интегральных уравнений

Напомним, что интегральным уравнением называют уравнение, в котором неизвестная функция входит под знак интеграла. Мы рассмотрим лишь уравнение вида (12)

называемое линейным интегральным уравнением Вольтерра второго рода с ядром K(t — т), зависящим от разности аргументов (уравнение типа свертки). Здесь φ(t) — искомая функция, f(t) и K(t) — заданные функции.

Пусть f(t) и K(t) есть функции-оригиналы, f(t) =’ F(p), K(t) =’ K(p).

Применяя к обеим частям (12) преобразование Лапласа и, пользуясь теоремой умножения, получим
(13)

где Ф(р) = φ(t). Из (13)

Оригинал для Ф(р) будет решением интегрального уравнения (12).

Пример:

Решить интегральное уравнение

Применяя преобразование Лапласа к обеим частям (14), получим

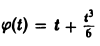
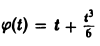
Функция является решением уравнения (14) (подстановка в уравнение (14) обращает последнее в тождество по t).

Замечание:

Преобразование Лапласа может быть использовано также при решении некоторых задач для уравнений математической физики.

Видео:6.1 Уравнение Лапласа в полярных координатах. Принцип решения и постановка задачСкачать

Таблица преобразования Лапласа

Видео:16. Решение уравнения Лапласа в цилиндре (старое занятие)Скачать

Дополнение к преобразованию Лапласа

Решение заданий и задач по предметам:

Дополнительные лекции по высшей математике:

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Видео:Задача Дирихле для круга. Уравнение ЛапласаСкачать

Боковая панель

Полное и подробное, насколько это возможно, решение уравнения Лапласа в сферических координатах, приводящее к шаровым и сферическим функциям. Всё самое интересное на, хоть и длинной, но одной странице. Много математики — много веселья!

Эту запись можно посмотреть в nbviewer.

Видео:Урок 5. Решение уравнения Лапласа в сферических координатахСкачать

Уравнение Лапласа в сферических координатах

Уравнение Лапласа в сферических координатах имеет вид

где $ r, vartheta = 90^circ — varphi, lambda $ — радиус, полярное расстояние (дополнение широты $varphi$ до $90^circ$), долгота соответственно.

Решить уравнение Лапласа это значит найти конкретный вид гармонической функции $f left( r, vartheta, lambda right)$, удовлетворяющей ему.

Прежде, чем переходить к решению, заметим важное и полезное свойство уравнения Лапласа: оно линейно. Это означает, что если есть два решения этого уравнения $f_1$ и $f_2$, то есть

$$ Delta f_1 = 0,qquad Delta f_2 = 0, $$

то их линейная комбинация

$$ f = alpha f_1 + beta f_2 $$

тоже является решением $Delta f = 0$.

Видео:Денисов А. М. - Уравнения математической физики. Лекции - Лекция 6Скачать

Разделение переменных

Будем искать решение уравнения Лапласа методом разделения переменных, суть которого в следующем. Представим искомую функцию $f$ трёх переменных $r, vartheta, lambda$ как произведение трёх других функций

begin f left(r, vartheta, lambda right) = R(r) cdot Theta left( vartheta right) cdot Lambda left( lambda right), end

каждая из которых теперь зависит только от одной переменной: $R$ есть функция только от $r$, $Theta$ есть функция только от $vartheta$, а $Lambda$ есть функция только от $lambda$. Стоит заметить, что не всякая система координат позволяет решить уравнение Лапласа методом разделения переменных, например этого нельзя сделать в геодезических координатах $H, B, L$.

Итак, делаем подстановку

Замечаем, что частные производные заменены на полные дифференциалы, поскольку функции $R, Theta, Lambda$ имеют только одну переменную. Разделим обе части уравнения на $RThetaLambda$ и умножим на $r^2$:

Первый член уравнения зависит только от $r$, а вся оставшаяся часть зависит только от угловых величин $vartheta, lambda$. Для того, чтобы равенство выполнялось необходимо, чтобы обе части равнялись некоторой постоянной $alpha$:

Первое уравнение будем называть радиальной частью уравнения Лапласа, поскольку она зависит только от $r$. Оставшуюся часть умножим на $sin^$ и запишем уравнение

которое является угловой частью уравнения Лапласа и называется дифференциальным уравнением сферических функций, поскольку, как увидим позже, именно они будут его решением.

И снова становится очевидным, что для сохранения равенства в полученном уравнении необходимо, чтобы обе части равнялись некоторой постоянной $beta$:

Таким образом, уравнение Лапласа, дифференциальное уравнение в частных производных второго порядка, разбивается на три обыкновенных дифференциальных уравнения второго порядка:

$$ begin r^2 frac <d^R><d r^> + 2 r frac — alpha R &= 0, label tag\ frac frac <d^Theta><d vartheta^> + frac< tan> frac- alpha Theta sin^- dfrac<sin> &= 0, label tag \ frac<d^Lambda><d lambda^> + beta Lambda &= 0. label tag end $$ Нам требуется теперь решить каждое из уравнений в отдельности, а заодно и определить вид постоянных $alpha$ и $beta$.

Отметим, что угловая часть уравнения Лапласа $Y (vartheta, lambda) = Theta (vartheta) Lambda (lambda)$ зависит только от полярного расстояния $vartheta$ и долготы $lambda$, то есть явялется функцией, заданной на сфере, следовательно решение этой части должно быть периодическим: $pi$ для широтной части и $2pi$ для долготной части. Только при этих условиях функция $Y (vartheta, lambda)$ может быть однозначно заданной на сфере.

Видео:Тихонов Н. А. - Методы математической физики - Уравнения эллиптического типаСкачать

Уравнение гармонических колебаний

Обыкновенное дифференциальное уравнение второго порядка вида

называется уравнением гармонических (или свободных) колебаний.

Оно имеет два линейно независимых решения при $beta > 0$

что легко проверяется подстановкой.

Как уже было сказано выше, для того, чтобы функция $Y left( vartheta, lambda right)$ была однозначной на сфере, необходимо, чтобы функция $Lambda$ имела период $2pi$. Из последнего уравнения нетрудно установить, что такое возможно только при $beta = m^2$, $m = 0, 1, 2, …$ Таким образом, решения уравнения гармонических колебаний принимают вид

линейная комбинация которых

является общим решением дифференциального уравнения. Здесь $C_1$ и $C_2$ — произвольные константы.

Видео:Колыбасова В.В. - Методы математической физики.Семинары - 15. Решение краевых задач. Функция ГринаСкачать

Присоединённое уравнение Лежандра

Перепишем второе уравнение, подставив в него значение $beta = m^2$:

И подставляя всё это, получим уравнение без тригонометрических функций в явном виде:

$$ left( 1 — t^2 right) dfrac

+ left[ alpha — dfrac right] P = 0. $$

Сначала установим некоторые свойства решения этого уравнения.

1. Во-первых, поскольку $t = cos$, то $-1 leq t leq +1$. Таким образом, областью определения $P (t)$ является интервал $[-1, 1]$.
2. Во-вторых, поскольку $0 leq vartheta leq pi$ и $-1 leq t leq +1$, то по теорема Вейерштрасса функция $P (t)$ является ограниченной и должна принимать некоторые конечные значения на этом интервале:

$$ left|P (-1)right| Сферические функции

Пользуясь полученными нами решениями уравнения гармонических колебаний и присоединённого уравнения Лежандра, мы можем записать теперь решение дифференциального уравнения для сферических функций (или угловой части уравнения Лапласа) в виде:

$$ Y_n^m left( vartheta, lambda right) = P_n^m (cos) cos ,qquad Y_n^m left( vartheta, lambda right) = P_n^m (cos) sin ,qquad $$

Функции такого вида называют элементарными сферическими функциями степени $n$ и порядка $m$. Видно, что степень и порядок элементарной сферической функции определяется степенью и порядком присоединённой функции Лежандра.

Поскольку дифференциальное уравнение для сферических функций является линейным, то и линейная комбинация его решений также будет решением. Эту комбинацию можно записать как

где $A_n^m$ и $B_n^m$ являются произвольными константами, которые ещё называют гармоническими коэффициентами или просто гармониками. Мы получили общее выражение для сферической функции степени $n$.

Видео:Семинар по УМФ, уравнение Лапласа 11.04.2020Скачать

Уравнение Коши-Эйлера

Наконец, найдём решение радиальной части уравнения Лапласа. Запишем её снова:

begin r^2 frac + 2 rfrac — alpha R = 0. end

Это уравнение Коши—Эйлера — линейное дифференциальное уравнение второго порядка с переменными коэффициентами. Будем искать решение в виде степенной функции $R = r^n$, тогда

Подставляем в дифференциальное уравнение и после тривиальных преобразований, получаем

begin n(n — 1) r^n + 2nr^n — alpha r^n = 0. end

Сокращаем на $r^n$, получаем характеристическое уравнение

begin n^2 + n — alpha = 0, end

два корня которого легко находим из решения квадратного уравнения

откуда, возвращаясь к нашей подстановке $R = r^n$, получаем два линейно независимых решения

Теперь, пользуясь значением для $alpha = n (n + 1)$, которое мы установили выше при рассмотрении присоединённого уравнения Лежандра, находим решения

линейная комбинация которых

по свойству линейных ОДУ второго порядка, является общим решением дифференциального уравнения. Здесь $C_1, C_2$ — произвольные постоянные.

Таким образом, мы получили решение радиальной (зависимой только от $r$) части уравнения Лапласа.

Видео:Радкевич Е.В. - Уравнения математической физики - 6.Задача Неймана для уравнения ЛапласаСкачать

Шаровые функции

Итак, мы решили все обыкновенные дифференциальные уравнения, возникшие после разделения переменных в уравнении Лапласа в сферических координатах. Осталось найти окончательный вид решения. Напоминаю, что искали мы его в виде

begin f left(r, vartheta, lambda right) = R(r) cdot Theta left( vartheta right) cdot Lambda left( lambda right) = R(r) cdot Y left( vartheta, lambda right). end

Подставляем сюда выражения eqref для $R$ и получаем два решения вида

begin f left(r, vartheta, lambda right) = r^ Y (vartheta, lambda),quad f left(r, vartheta, lambda right) = r^ Y (vartheta, lambda), end

которые называются шаровыми функциями (solid spherical harmonics), а функции $Y (vartheta, lambda)$ — сферическими (spherical harmonics). Таким образом, последние два выражения устанавливают связь шаровых и сферических функций.

Используя общее выражение для сферической функции степени $n$ eqref, шаровые функции можно записать так

begin f left(r, vartheta, lambda right) &= r^ sumlimits_^n (A_n^m cos + B_n^m sin) P_n^m (cos),\ f left(r, vartheta, lambda right) &= dfrac<r^> sumlimits_^n (A_n^m cos + B_n^m sin) P_n^m (cos). end

Вспоминая свойство линейности, о котором мы упоминали в самом начале, можно записать общее решение уравнения Лапласа, как линейную комбинацию частных решений в виде ряда по степеням $n$:

begin f left(r, vartheta, lambda right) &= sumlimits_^ r^ sumlimits_^n (A_n^m cos + B_n^m sin) P_n^m (cos),\ f left(r, vartheta, lambda right) &= sumlimits_^ dfrac<r^> sumlimits_^n (A_n^m cos + B_n^m sin) P_n^m (cos). end

Эти выражения называются рядами шаровых функций, а при $r = 1$ они обратятся в ряды сферических функций или ряды Лапласа.

Ряды шаровых функций и являются решением уравнения Лапласа в сферических координатах.

Для геодезии, изучающей внешнее гравитационное поле, куда более важными являются шаровые функции вида $f = r^ Y_n (vartheta, lambda)$, через которые может быть выражен потенциал притяжения вне притягивающих масс, поскольку $r$ здесь, как и у потенциала притяжения стоит в знаменателе. Вообще говоря, любая гармоническая вне сферы функция $f_e$ ($e$, external) может быть разложена в ряд

$$ f_e = sumlimits_^ r^ Y_n (vartheta, lambda) $$,

а любая гармоническая внутри сферы функция $f_i$ ($i$, internal) может быть разложена в ряд

$$ f_i = sumlimits_^ r^n Y_n (vartheta, lambda).$$

🌟 Видео

Уравнения математической физики. Уравнение Лапласа. Часть 2Скачать

Метод Лапласа решения ДУСкачать

6.2 Решение задач для уравнения Лапласа в круге, вне круга и в кольцеСкачать

Уравнения математической физики 15+16 Задача Дирихле для уравнения Лапласа - Пуассона в кругеСкачать