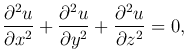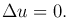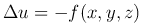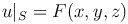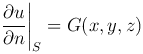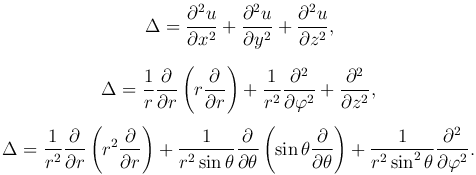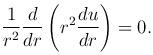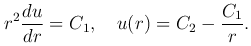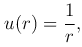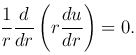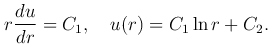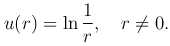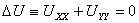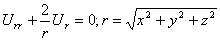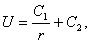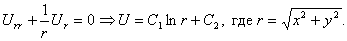Рассмотрим уравнение с частными производными вида
где u=u(x, y, z). Это уравнение называется уравнением Лапласа.
Левая часть обозначается Δu и называется оператором Лапласа. Таким образом, это уравнение преобразуется к виду:
Данному уравнению удовлетворяет потенциал скорости безвихревого течения несжимаемой (с постоянной плотностью) жидкости; потенциал сил тяготения или сил взаимодействия электрических зарядов во всех точках пространства, находящихся вне притягивающих масс или вне зарядов, создающих поле; температура в однородном теле, если теплообмен является стационарным, т.е. температура u зависит только от места, но не от времени и др.
называется уравнением Пуассона.
Уравнение Лапласа и уравнение Пуассона является уравнениями эллиптического типа.
Определение. Функцию, непрерывную в некоторой области вместе со своими частными производными до второго порядка включительно и удовлетворяющую уравнению Лапласа, называют гармонической.
Обычно в задачах, связанных с уравнением Лапласа или Пуассона, искомое решение должно удовлетворять уравнению в области D, а также некоторому дополнительному условию на границе S области D.
Если надо определить функцию, гармоническую в области D, когда на границе S области D заданы ее значения, т.е.
(первая краевая задача), то такая задача называется задачей Дирихле.
Если же надо определить функцию, гармоническую в области D, когда на границе S задается значение нормальной производной
(вторая краевая задача), то такая задача называется задачей Неймана.
Определение. Если решение задачи ищут в области D, внутренней (внешней) по отношению к поверхности S, то соответствующую задачу называют внутренней (внешней) краевой задачей.
Видео:Радкевич Е.В. - Уравнения математической физики - 4.Фундаментальное решение уравнения ЛапласаСкачать
Фундаментальные решения уравнения Лапласа
Рассмотрим уравнение Лапласа
где оператор Лапласа в декартовой, цилиндрической и сферической системах координат определяется соответственно
Важную роль при решении задач для уравненийй Лапласа и Пуассона представляют решения, обладающие сферической или цилиндрической симметрией.
Найдем решение уравнения Лапласа, удовлетворяющее условию сферической симметрии, когда функция u зависит только от расстояния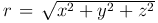 
точки M(x, y, z) до начала координат. В этом случае уравнение Лапласа в сферической системе координат имеет вид
Интегрируя это уравнение, получим
которая удовлетворяет уравнению Лапласа всюду, кроме точки r=0, где она обращается в бесконечность. Такую функцию называют фундаментальным решением уравнения Лапласа в пространстве.
В задаче с осевой симметрией, когда функция u в цилиндрической системы координат не зависит от φ и z, уравнение Лапласа имеет вид
Интегрируя это уравнение, получим
Эта функция называется фундаментальным решением уравнения Лапласа на плоскости.
Видео:7.1 Решение уравнения Лапласа в прямоугольникеСкачать
Лекция 7. Гармонические функции и их свойства
Рассмотрим уравнение Лапласа на плоскости
и в пространстве
Уравнение (33) при переходе к полярным координатам преобразуется к виду
Рис 14 Рис 14.1
Если в пространстве перейти к сферическим координатам
то уравнение (34) примет вид
Функции U=U(x,y) на плоскости и U=U(x,y,z) в пространстве, имеющие непрерывные частные производные второго порядка и удовлетворяющие, соответственно, уравнению Лапласа (33) или (34) в некоторой области D, называются гармоническими в этой области. Простейшими примерами гармонических функций являются линейные функции: U = ах + by + с на плоскости и U = ax + by + cz + d в пространстве. Особый интерес представляют решения уравнения Лапласа, обладающие сферической или цилиндрической (в случае двух независимых переменных — круговой) симметрией.
Решение U=U(r), обладающее сферической симметрией, будет определяться из обыкновенного дифференциального уравнения
Это уравнение получится, если подставить искомую функцию в уравнение Лапласа (34*), записанное в сферических координатах. Интегрируя это уравнение, находим
где C1 и C2 — произвольные постоянные. Полагая C1=1, C2=0, получим функцию
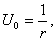
которую часто называют фундаментальным решением уравнения Лапласа в пространстве. Функция U0 является гармонической всюду в пространстве, кроме начала координат 0.
Аналогично, полагая U=U(r) и пользуясь уравнением Лапласа в цилиндрических или полярных координатах, найдем решения, обладающие цилиндрической или круговой симметрией:
Выбирая С1=-1 и С2=0, будем иметь функцию 
Рассмотрим в пространстве электрическое поле, образованное точечным зарядом величины q , помещенным в начало координат. Тогда потенциал этого поля равен
Аналогично, если рассмотреть поле, создаваемое заряженной прямой, то потенциал такого поля будет равен
где q1 — линейная плотность заряда (то есть заряд, рассчитанный на единицу длины).
Более сложные примеры будут рассмотрены далее, а сейчас изучим свойства гармонических функций.
Теорема о среднем. Пусть функция U=U(x,y) гармоническая в некотором круге D радиуса R с центром (хo,уo) и непрерывная в соответствующем замкнутом круге Тогда значение этой функции в центре круга равно ее среднему значению на окружности Г, ограничивающей данный круг, то есть
При доказательстве этой теоремы применим интегральную формулу Пуассона для круга, которая будет доказана позже в лекции 10. Она имеет вид (см. рис. 15)
Если в этой формуле положить ρ=0, то получится формула (35).
Теорему о среднем можно представить и в другой форме. Для этого запишем формулу (35) для произвольного круга радиуса r, где 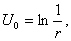(см. рис.15.1):
Умножив обе части равенства (36) на rdr и проинтегрировав по r в пределах от 0 до R, получим:
где D — круг радиуса R. Разделив обе части полученного равенства на R 2 /2 , будем иметь
В правой части формулы (37) записано среднее значение гармонической функции U(x,y) в круге радиуса R.
Имеет место и обратная теорема: если в некоторой области D функция U=U(x,y) непрерывная и для каждой точки выполняется теорема о среднем в любом сколь угодно малом круге с центром в точке (хо, уо), то эта функция гармоническая в D. Из формулы (37) получается:
Следствие. Если функция U=U(x,y) гармоническая в некотором круге D радиуса R и непрерывная в соответствующем замкнутом круге ,то
Число называют нормой функции U=U(x,y) в области D , и неравенство (38) можно переписать в виде
Неравенство (38) доказывается совсем просто, если воспользоваться известным неравенством Коши-Буняковского:
Применим это неравенство к формуле (37):
Что и требовалось доказать.
Гармонические функции, помимио вышеуказанных свойств, обладают и многими другими свойствами. Приведем еще два из них.
Неравенство Харнака. Пусть функция гармоническая в некотором круге D радиуса R c центром (xo, уo) и непрерывная в соответствующем круге Тогда при любом она удовлетворяет неравенству
Из неравенства Харнака следует теорема Лиувилля.
Теорема Лиувилля. Гармоническая на всей плоскости функция U=U(x, у) не может быть ограниченной сверху или снизу, если она не постоянная.
Доказательство. Если функция U=U(x, у) ограничена сверху, то U1=-U(x, y) — ограничена снизу и тоже гармоническая. Поэтому достаточно рассмотреть случай, когда функция ограничена снизу: Более того, можно считать, что M=0. Действительно, ,а разность (U-M) тоже гармоническая функция. Итак, предполагая существование гармонической во всей плоскости неотрицательной функции U(x, у), мы докажем, что эта функция постоянная.
Воспользуемся неравенством Харнака
Если функция U(x, у) гармоническая во всей плоскости то, фиксировав произвольное и неограниченно увеличивая R мы получим
то есть Теорема Лиувилля доказана.
Замечание. Гармонические функции в пространстве обладают аналогичными свойсвами. Приведем формулировку одного из них.
Терема о среднем. Пусть функция U=U(x, у) гармоническая в некотором шаре D радиуса R c центром
(xo , уo , zo ) и непрерывная в соответствующем замкнутом шаре Тогда значение этой функции в центре шара равно:
а) ее среднему значению на сфере Г, ограничивающей данный шар, то есть
б) ее среднему значению в шаре D, то есть
Видео:Лекция: Фундаментальное решение оператора ЛапласаСкачать
Боковая панель
Полное и подробное, насколько это возможно, решение уравнения Лапласа в сферических координатах, приводящее к шаровым и сферическим функциям. Всё самое интересное на, хоть и длинной, но одной странице. Много математики — много веселья!
Эту запись можно посмотреть в nbviewer.
Видео:Преобразование Лапласа - bezbotvyСкачать
Уравнение Лапласа в сферических координатах
Уравнение Лапласа в сферических координатах имеет вид
где $ r, vartheta = 90^circ — varphi, lambda $ — радиус, полярное расстояние (дополнение широты $varphi$ до $90^circ$), долгота соответственно.
Решить уравнение Лапласа это значит найти конкретный вид гармонической функции $f left( r, vartheta, lambda right)$, удовлетворяющей ему.
Прежде, чем переходить к решению, заметим важное и полезное свойство уравнения Лапласа: оно линейно. Это означает, что если есть два решения этого уравнения $f_1$ и $f_2$, то есть
$$ Delta f_1 = 0,qquad Delta f_2 = 0, $$
то их линейная комбинация
$$ f = alpha f_1 + beta f_2 $$
тоже является решением $Delta f = 0$.
Видео:Денисов А. М. - Уравнения математической физики. Лекции - Лекция 6Скачать
Разделение переменных
Будем искать решение уравнения Лапласа методом разделения переменных, суть которого в следующем. Представим искомую функцию $f$ трёх переменных $r, vartheta, lambda$ как произведение трёх других функций
begin f left(r, vartheta, lambda right) = R(r) cdot Theta left( vartheta right) cdot Lambda left( lambda right), end
каждая из которых теперь зависит только от одной переменной: $R$ есть функция только от $r$, $Theta$ есть функция только от $vartheta$, а $Lambda$ есть функция только от $lambda$. Стоит заметить, что не всякая система координат позволяет решить уравнение Лапласа методом разделения переменных, например этого нельзя сделать в геодезических координатах $H, B, L$.
Итак, делаем подстановку
Замечаем, что частные производные заменены на полные дифференциалы, поскольку функции $R, Theta, Lambda$ имеют только одну переменную. Разделим обе части уравнения на $RThetaLambda$ и умножим на $r^2$:
Первый член уравнения зависит только от $r$, а вся оставшаяся часть зависит только от угловых величин $vartheta, lambda$. Для того, чтобы равенство выполнялось необходимо, чтобы обе части равнялись некоторой постоянной $alpha$:
Первое уравнение будем называть радиальной частью уравнения Лапласа, поскольку она зависит только от $r$. Оставшуюся часть умножим на $sin^$ и запишем уравнение
которое является угловой частью уравнения Лапласа и называется дифференциальным уравнением сферических функций, поскольку, как увидим позже, именно они будут его решением.
И снова становится очевидным, что для сохранения равенства в полученном уравнении необходимо, чтобы обе части равнялись некоторой постоянной $beta$:
Таким образом, уравнение Лапласа, дифференциальное уравнение в частных производных второго порядка, разбивается на три обыкновенных дифференциальных уравнения второго порядка:
$$ begin r^2 frac <d^R><d r^> + 2 r frac — alpha R &= 0, label tag\ frac frac <d^Theta><d vartheta^> + frac< tan> frac- alpha Theta sin^- dfrac<sin> &= 0, label tag \ frac<d^Lambda><d lambda^> + beta Lambda &= 0. label tag end $$ Нам требуется теперь решить каждое из уравнений в отдельности, а заодно и определить вид постоянных $alpha$ и $beta$.
Отметим, что угловая часть уравнения Лапласа $Y (vartheta, lambda) = Theta (vartheta) Lambda (lambda)$ зависит только от полярного расстояния $vartheta$ и долготы $lambda$, то есть явялется функцией, заданной на сфере, следовательно решение этой части должно быть периодическим: $pi$ для широтной части и $2pi$ для долготной части. Только при этих условиях функция $Y (vartheta, lambda)$ может быть однозначно заданной на сфере.
Видео:Уравнения математической физики. Уравнение Лапласа. Часть 1Скачать
Уравнение гармонических колебаний
Обыкновенное дифференциальное уравнение второго порядка вида
называется уравнением гармонических (или свободных) колебаний.
Оно имеет два линейно независимых решения при $beta > 0$
что легко проверяется подстановкой.
Как уже было сказано выше, для того, чтобы функция $Y left( vartheta, lambda right)$ была однозначной на сфере, необходимо, чтобы функция $Lambda$ имела период $2pi$. Из последнего уравнения нетрудно установить, что такое возможно только при $beta = m^2$, $m = 0, 1, 2, …$ Таким образом, решения уравнения гармонических колебаний принимают вид
линейная комбинация которых
является общим решением дифференциального уравнения. Здесь $C_1$ и $C_2$ — произвольные константы.
Видео:Решение уравнения Лапласа в шареСкачать
Присоединённое уравнение Лежандра
Перепишем второе уравнение, подставив в него значение $beta = m^2$:
И подставляя всё это, получим уравнение без тригонометрических функций в явном виде:
$$ left( 1 — t^2 right) dfrac
Сначала установим некоторые свойства решения этого уравнения.
- Во-первых, поскольку $t = cos$, то $-1 leq t leq +1$. Таким образом, областью определения $P (t)$ является интервал $[-1, 1]$.
- Во-вторых, поскольку $0 leq vartheta leq pi$ и $-1 leq t leq +1$, то по теорема Вейерштрасса функция $P (t)$ является ограниченной и должна принимать некоторые конечные значения на этом интервале:
$$ left|P (-1)right| Сферические функции
Пользуясь полученными нами решениями уравнения гармонических колебаний и присоединённого уравнения Лежандра, мы можем записать теперь решение дифференциального уравнения для сферических функций (или угловой части уравнения Лапласа) в виде:
$$ Y_n^m left( vartheta, lambda right) = P_n^m (cos) cos ,qquad Y_n^m left( vartheta, lambda right) = P_n^m (cos) sin ,qquad $$
Функции такого вида называют элементарными сферическими функциями степени $n$ и порядка $m$. Видно, что степень и порядок элементарной сферической функции определяется степенью и порядком присоединённой функции Лежандра.
Поскольку дифференциальное уравнение для сферических функций является линейным, то и линейная комбинация его решений также будет решением. Эту комбинацию можно записать как
где $A_n^m$ и $B_n^m$ являются произвольными константами, которые ещё называют гармоническими коэффициентами или просто гармониками. Мы получили общее выражение для сферической функции степени $n$.
Видео:Горицкий А. Ю. - Уравнения математической физики. Часть 2 -Фундаментальное решение оператора ЛапласаСкачать
Уравнение Коши-Эйлера
Наконец, найдём решение радиальной части уравнения Лапласа. Запишем её снова:
begin r^2 frac + 2 rfrac — alpha R = 0. end
Это уравнение Коши—Эйлера — линейное дифференциальное уравнение второго порядка с переменными коэффициентами. Будем искать решение в виде степенной функции $R = r^n$, тогда
Подставляем в дифференциальное уравнение и после тривиальных преобразований, получаем
begin n(n — 1) r^n + 2nr^n — alpha r^n = 0. end
Сокращаем на $r^n$, получаем характеристическое уравнение
begin n^2 + n — alpha = 0, end
два корня которого легко находим из решения квадратного уравнения
откуда, возвращаясь к нашей подстановке $R = r^n$, получаем два линейно независимых решения
Теперь, пользуясь значением для $alpha = n (n + 1)$, которое мы установили выше при рассмотрении присоединённого уравнения Лежандра, находим решения
линейная комбинация которых
по свойству линейных ОДУ второго порядка, является общим решением дифференциального уравнения. Здесь $C_1, C_2$ — произвольные постоянные.
Таким образом, мы получили решение радиальной (зависимой только от $r$) части уравнения Лапласа.
Видео:Задача Дирихле для круга. Уравнение ЛапласаСкачать
Шаровые функции
Итак, мы решили все обыкновенные дифференциальные уравнения, возникшие после разделения переменных в уравнении Лапласа в сферических координатах. Осталось найти окончательный вид решения. Напоминаю, что искали мы его в виде
begin f left(r, vartheta, lambda right) = R(r) cdot Theta left( vartheta right) cdot Lambda left( lambda right) = R(r) cdot Y left( vartheta, lambda right). end
Подставляем сюда выражения eqref для $R$ и получаем два решения вида
begin f left(r, vartheta, lambda right) = r^ Y (vartheta, lambda),quad f left(r, vartheta, lambda right) = r^ Y (vartheta, lambda), end
которые называются шаровыми функциями (solid spherical harmonics), а функции $Y (vartheta, lambda)$ — сферическими (spherical harmonics). Таким образом, последние два выражения устанавливают связь шаровых и сферических функций.
Используя общее выражение для сферической функции степени $n$ eqref, шаровые функции можно записать так
begin f left(r, vartheta, lambda right) &= r^ sumlimits_^n (A_n^m cos + B_n^m sin) P_n^m (cos),\ f left(r, vartheta, lambda right) &= dfrac<r^> sumlimits_^n (A_n^m cos + B_n^m sin) P_n^m (cos). end
Вспоминая свойство линейности, о котором мы упоминали в самом начале, можно записать общее решение уравнения Лапласа, как линейную комбинацию частных решений в виде ряда по степеням $n$:
begin f left(r, vartheta, lambda right) &= sumlimits_^ r^ sumlimits_^n (A_n^m cos + B_n^m sin) P_n^m (cos),\ f left(r, vartheta, lambda right) &= sumlimits_^ dfrac<r^> sumlimits_^n (A_n^m cos + B_n^m sin) P_n^m (cos). end
Эти выражения называются рядами шаровых функций, а при $r = 1$ они обратятся в ряды сферических функций или ряды Лапласа.
Ряды шаровых функций и являются решением уравнения Лапласа в сферических координатах.
Для геодезии, изучающей внешнее гравитационное поле, куда более важными являются шаровые функции вида $f = r^ Y_n (vartheta, lambda)$, через которые может быть выражен потенциал притяжения вне притягивающих масс, поскольку $r$ здесь, как и у потенциала притяжения стоит в знаменателе. Вообще говоря, любая гармоническая вне сферы функция $f_e$ ($e$, external) может быть разложена в ряд
$$ f_e = sumlimits_^ r^ Y_n (vartheta, lambda) $$,
а любая гармоническая внутри сферы функция $f_i$ ($i$, internal) может быть разложена в ряд
$$ f_i = sumlimits_^ r^n Y_n (vartheta, lambda).$$
🎦 Видео
Олегу Тинькову запрещён вход на Мехмат МГУСкачать
Преобразование Лапласа по определениюСкачать
Уравнение Лапласа (ФКП)Скачать
6.1 Уравнение Лапласа в полярных координатах. Принцип решения и постановка задачСкачать
6.2 Решение задач для уравнения Лапласа в круге, вне круга и в кольцеСкачать
Метод Лапласа решения ДУСкачать
16. Решение уравнения Лапласа в цилиндре (старое занятие)Скачать
Уравнения математической физики. Уравнение Лапласа. Часть 2Скачать
Математика без Ху!ни. Метод Гаусса. Совместность системы. Ранг матрицы.Скачать
