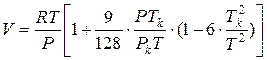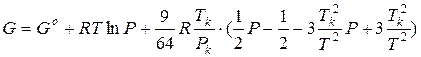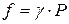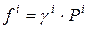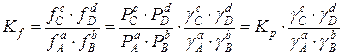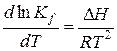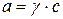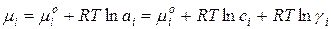В работах по химической термодинамике для формального описания зависимости химического потенциала реального газа от давления пользуются методом Льюиса (1901), согласно которому вводится новая функция f, которая называется фугитивностью или летучестью и имеет размерность давления:
(p, T) = (T) + RT ln f(p, T). (1.45)
Выражение (1.45) аналогично зависимости химического потенциала идеального газа от давления. Однако аналогия эта чисто формальна, поскольку фугитивность является функцией давления и температуры, причем характер зависимости f(p, T) индивидуален и зависит от природы газа. Коэффициентом фугитивности называется безразмерная величина
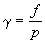
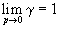
Из уравнений (1.43) и (1.45) вытекает:
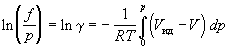
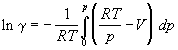
Используя определение фактора сжимаемости Z = pV/RT, уравнение (1.47) можно записать в виде:
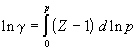
Используя уравнения (1.46) – (1.48), можно рассчитать фугитивность реальных газов графическими или аналитическими методами.
1.7.1. Графические методы
Графические методы используют для определения фугитивности чистого газа по экспериментальным данным об его объеме V при различных давлениях p и T = const.
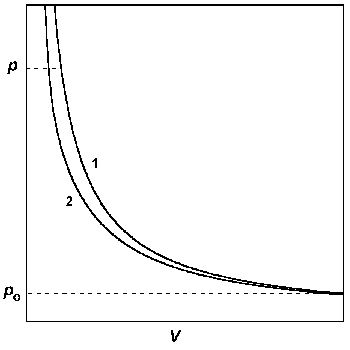
А) В координатах p – V строят изотермы идеального и реального газов от достаточно низкого давления, при котором эти изотермы практически сливаются, до давления, при котором требуется определить фугитивность. Интеграл в правой части уравнения (1.46) определяют графически (рис. 1.7).
Видео:ФИЗИЧЕСКАЯ ХИМИЯ (ТЕРМОДИНАМИКА). ОСНОВНЫЕ ПОНЯТИЯ: СИСТЕМЫ, ПАРАМЕТРЫ, ФУНКЦИИСкачать

Рис.1.7. Графический метод определения фугитивности: построение р — V изотерм для идеального (1) и реального (2) газов.
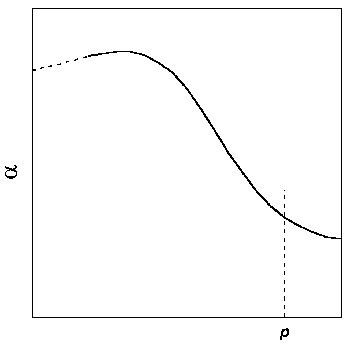
Б) Вычисляют объемную поправку реального газа , равную подынтегральному выражению в уравнениях (1.46) и (1.47):
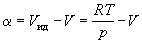
Затем строят зависимость от p при заданной температуре и интеграл в правой части уравнения (1.47) определяют графически(рис. 1.8).
Рис.1.8. Графический метод определения фугитивности: построение зависимости от р
Преимущества метода Б) по сравнению с методом А) заключаются в следующем. Во-первых, интервал изменения значительно меньше, чем V, особенно при высоких температурах. Во-вторых, при p 

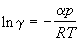

При низких p экспоненту можно разложить в ряд, ограничившись двумя членами:
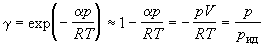
где pид – давление, которое имел бы идеальный газ, если бы он занимал тот же объем, что и реальный. С помощью уравнения (1.52) можно приближенно вычислять фугитивность при низких давлениях.
Смысл поправки при p 0 наглядно проявляется при использовании вириального уравнения состояния. При низких давлениях в уравнении (1.16) можно ограничиться членом со вторым вириальным коэффициентом, т.е.
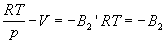
Таким образом, при p 0 поправка равна второму вириальному коэффициенту со знаком «минус». [Отметим, что при любых конечных значениях в пределе p 0 получается уравнение состояния идеального газа, поскольку RT – pV = p, и, следовательно, 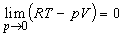
1.7.2. Аналитические методы
А). Аналитические методы основаны на подстановке в соотношение (1.47) уравнения состояния реального газа и аналитическом вычислении интеграла в правой части. Например, для газа Ван-дер-Ваальса после интегрирования получаем
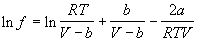
Точность расчета фугитивности будет определяться точностью используемого уравнения состояния в исследуемом интервале p и T.
Б). Фугитивность газа можно приближенно определить на основе закона соответственных состояний (метод Ньютона). Согласно закону соответственных состояний, коэффициент фугитивности является универсальной функцией приведенных давления pr и температуры Tr. Зависимость ( pr, Tr) представляют в виде обобщенных диаграмм или уравнений, из которых легко определить коэффициент фугитивности (и фугитивность f = p), зная критические параметры газа.
Задачи и упражнения к главе 1
Видео:ЕГЭ. Физика. Основы термодинамики. Законы термодинамики. ПрактикаСкачать

* Задачи, помеченные звездочкой, рекомендуется решать с помощью компьютера, оснащенного программой графической обработки экспериментальных данных, например, Excel, Origin или SigmaPlot.
1.1. Выразите уравнение состояния Ван-дер-Ваальса в виде вириального разложения по степеням 1/Vm и получите выражения для вириальных коэффициентов B2 и B3 через параметры a и b. Воспользуйтесь разложением: 1/(1–x) = 1 + x + x 2 + .
1.2. Уравнения (1.15) и (1.16) являются разложениями по степеням 1/Vm и p, соответственно. Найдите соотношение между B2, B3 и B2‘, B3‘.
1.3. Предложено следующее уравнение состояния:
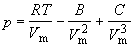
Покажите, что это уравнение приводит к критическому поведению. Выразите критические константы газа через параметры B и C и получите выражение для фактора сжимаемости в критической точке.
1.4. Покажите, что для газа с жесткими молекулами сферической формы при учете только парных взаимодействий константа b в уравнении Ван-дер-Ваальса равна учетверенному собственному мольному объему молекул. Оцените значение b для Ne, если его молекулярный диаметр равен 0.258 нм.
1.5.* Покажите, что второй вириальный коэффициент и молярную массу газа можно получить, строя график p/ от p, где p – давление газа, – его плотность. Рассчитайте B2 для диметилового эфира, пользуясь следующими данными:
| р,Торр | 91,74 | 188,98 | 277,3 | 452,8 | 639,3 | 760,0 |
| ,г/л | 0,232 | 0,489 | 0,733 | 1,25 | 1,87 | 2,30 |
1.6.* Рассчитайте второй вириальный коэффициент для водорода при 0° C, пользуясь следующими данными:
| р, бар | 50,7 | 101,3 | 202,6 | 303,9 |
| V,л/моль | 0,4634 | 0,2386 | 0,1271 | 0,090 |
1.7.* Пользуясь правилом прямолинейного диаметра [уравнение (1.2)], определите критический мольный объем CCl4, используя следующие данные:
| t, o C | 100 | 150 | 200 | 250 | 270 | 280 |
| ж,г/см 3 | 1,4343 | 1,321 | 1,1888 | 0,9980 | 0,8666 | 0,7634 |
| п, г/см 3 | 0,0103 | 0,0304 | 0,0742 | 0,1754 | 0,2710 | 0,3597 |
Критическая температура CCl4 равна 283,1 o C.
1.8. Найдите 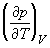
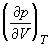
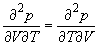
1.9. Выведите выражение для работы изотермического обратимого расширения газа, подчиняющегося уравнению состояния Ван-дер-Ваальса.
1.10. Выведите выражение для работы изотермического обратимого расширения газа, подчиняющегося вириальному уравнению состояния (1.15).
1.11. Второй и третий вириальные коэффициенты в уравнении (1.15) для аргона при 273 К равны соответственно В2 = – 21,7 см 3 /моль и В3 = 1200 см 6 /моль 2 . Рассчитайте: а) работу обратимого изотермического расширения при этой температуре, б) работу расширения против постоянного давления 1 атм и в) работу расширения в предположении, что аргон ведет себя идеально. Примите, что Vm,1 = 500 см 3 и Vm,2 = 1000 см 3 .
1.12. Покажите, что работа изотермического обратимого расширения газа Ван-дер-Ваальса может быть выражена в виде приведенных переменных и что, определив приведенную работу как Ar = A3b/a, можно получить выражение, не зависящее от природы газа.
Видео:Урок 172. Применение 1 закона термодинамики для различных процессовСкачать

Литература к главе 1
1.М.П. Вукалович, И.И. Новиков
Уравнение состояния реальных газов
М.-Л., Госэнергоиздат, 1948.
2.В.И. Горшков, И.А. Кузнецов
Основы физической химии
М.: Изд-во Моск. ун-та, 1993.
3.Физическая химия / под ред. Б.П. Никольского
Л.: Химия, 1987.
4.Курс физической химии / под ред. Я.И. Герасимова. Т. 1
М.: Госхимиздат, 1963.
5.Е.Н. Еремин.
Основы химической термодинамики
М.: Высшая школа, 1978.
6.Е.М. Кузнецова, Е.П. Агеев
Термодинамика в вопросах и ответах
М.: Химический факультет МГУ, 1997.
7.Э. Мейсон, Е. Сперлинг
Вириальное уравнение состояния
М.: Мир, 1972
8.О.М. Полторак
Термодинамика в физической химии
М.: Высшая школа, 1991.
9.R.A. Alberty, R.J. Silbey
Physical Chemistry
Wiley, New York, 1997.
10.P.W. Atkins
Physical Chemistry
Oxford University Press, 1994.


Сервер создается при поддержке Российского фонда фундаментальных исследований
Не разрешается копирование материалов и размещение на других Web-сайтах
Вебдизайн: Copyright (C) И. Миняйлова и В. Миняйлов
Copyright (C) Химический факультет МГУ
Написать письмо редактору
Фугитивность
Фугит и вность, величина, используемая для расчёта свойств реальных газов с помощью термодинамических соотношений, выведенных для идеальных газов (см. также Газы); введена Г. Льюисом в 1901. Фугитивность f данного газа (компонента газовой смеси) — такая функция давления p, температуры Т (и концентрации каждого из компонентов смеси), подстановка которой вместо давления (парциального давления) в термодинамическом уравнения для идеального газа делает их справедливыми и для реального газа при рассматриваемых условиях. Хотя этот приём является формально-математическим, однако он продуктивен, т.к. применение более сложных уравнений состояния реальных газов, во-первых, связано со значительными вычислительными трудностями и, во-вторых, не может обеспечить необходимую точность, поскольку любое уравнение состояния реального газа справедливо лишь в определённом интервале значений p и Т.
Отношение f/p называется коэффициентом фугитивности; очевидно, для идеального газа он при любых условиях равен 1. Т. о., отличие значения f/p от 1 характеризует степень отклонения газа от идеального состояния. Роль фугитивности газа по отношению к его парциальному давлению аналогична роли активности компонента раствора по отношению к его концентрации.
Поскольку фугитивность вещества, образующего конденсированную фазу или входящего в её состав, равна его фугитивности в насыщенном паре этой фазы, то фугитивность можно рассматривать и как величину, количественно характеризующую при заданных p, Т и составе фазы способность вещества к выходу из неё (отсюда и название: лат. fugitivus — убежавший, улетевший).
ТЕРМОДИНАМИКА РАВНОВЕСИЙ В РЕАЛЬНЫХ ГАЗОВЫХ СИСТЕМАХ. ФУГИТИВНОСТЬ И АКТИВНОСТЬ.
Чтобы проинтегрировать какое-либо термодинамическое выражение функции, например: 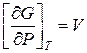
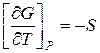
Для идеальных газов: PV=RT 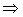
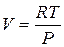
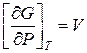
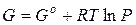
Для чистого реального газа, состояние которого описывается уравнением Бертло:
Интегрируем и получаем:
(при интегрировании принято P o = Pстанд = 1 атм).
Видео:ФИЗИКА ЗА 5 МИНУТ - ТЕРМОДИНАМИКАСкачать

Расчеты по таким уравнениям трудны и их точность ограничена точностью входящих в них эмпирических констант.
По этой причине вместо давления вводят величину, называемую фугитивностью или летучестью f. Фугитивность имеет размерность давления (Па, атм) и связана с давлением реального газа следующим соотношением:
где γ – безразмерный коэффициент фугитивности,зависящий от давления и температуры 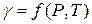
Фугитивность – это такое давление реального газа, при котором газ ведет себя как идеальный.
При f→P свойства реальных газов приближаются к свойствам идеальных газов, а коэффициент фугитивности стремится к единице γ→1.
В реальной газовой смеси парциальная фугитивность i-го компонента равна:
где Рi – парциальное давление i-го компонента в смеси газов.
Применение фугитивности вместо парциальных давлений практикуется при относительно высоких давлениях и низких температурах, когда наблюдаются значительные отклонения от идеальности.
Для 1 моль чистого газа:
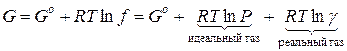
Для 1 моль i-го газа в смеси:
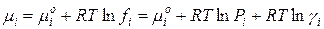
где µi 0 – стандартный химический потенциал i-го компонента при Р=1 атм, Т=298 К и γ=1.
На основании данных по фугитивности при помощи уравнения (2) можно определить константу равновесия для реального газа.
Видео:Применение первого закона термодинамики к изопроцессам. 10 класс.Скачать

Kf – термодинамическая константа равновесия (безразмерная величина).
Уравнение изобары Вант-Гоффа:
Kf ≠ f (P); Kp=Kf только при малых давлениях, когда реальная газовая смесь приближается к идеальному состоянию.
Тесно связана с фугитивностью и величина активности:
где с – концентрация газа или реального раствора.
Величина активности используется не только применительно к реальным газам, но и к реальным растворам.
γ – безразмерный коэффициент активности, зависит от с и Т, т.е. γ = f (с,Т).
Активность – это такая концентрация, при использовании которой реальные растворы приобретают термодинамические свойства идеальных растворов. Активность имеет размерность концентрации.
Химический потенциал i-го компонента в растворе можно выразить:
где µi 0 – стандартный химический потенциал, когда активность i-го компонента равна единице ai = 1.
Для химических реакций в реальных растворах константу равновесия можно выразить следующим образом:
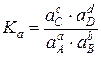
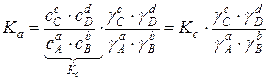
Видео:Физика 10 класс (Урок№24 - Первый закон термодинамики.)Скачать

γ – коэффициенты активности для исходных веществ и продуктов реакции.
Таким образом, равновесие химической реакции в зависимости от условий, можно выразить константами равновесия: Kp, Kc, KN, Kf и Ka.
Несмотря на различия констант в различных типах химических реакций, суть у них одна: количественное определение условий равновесия в обратимых процессах.
Дата добавления: 2016-02-02 ; просмотров: 2786 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
🌟 Видео
Применение первого начала термодинамики к изопроцессамСкачать

Законы Термодинамики. Что Такое Термодинамика?Скачать

Изопроцессы с идеальным газом. Первое начало термодинамики | Физика, онлайн-форумСкачать

Консультация по термодинамике. Часть 1Скачать

Тема 11. Работа в термодинамике. Решение задач по теме «Работа в термодинамике»Скачать

Основы химической термодинамикиСкачать

Работа, совершаемая при термодинамических процессах. 10 класс.Скачать

Коробов М. В. - Физическая химия. Часть 1 - Основные понятия, свойства системыСкачать
Энергия Гиббса и Гельмгольца.Фугитивность и активность.Термодинамические потенциалы.Скачать

Введение в парциальное давление | Газы.Молекулярно-кинетическая теория | ХимияСкачать

ФИЗИЧЕСКАЯ ХИМИЯ. ПЕРВЫЙ ЗАКОН ТЕРМОДИНАМИКИ и ИЗОПРОЦЕССЫ. РАБОТА ГАЗАСкачать

Все самые важные процессы в термодинамике | Физика ЕГЭ 2023 | УмскулСкачать

Коробов М. В. - Физическая химия. Часть 1 - Характеристические функцииСкачать

Урок 169. Задачи на вычисление работы в термодинамикеСкачать