Фср и общее решение лоду в случае кратных действительных корней характеристического уравнения

Опр: Система n линейно-независимого решения ЛОДУ n-го порядка называется ФСР

Теорема о структуре общего решения ЛОДУ

Если функции y₁(х)_, y₂(х)_, … ,y_n(х) – образует ФСР ЛОДУ у ( n ) + P₁y ( n -1) +…+ P_n-1 y’ + P_n y = 0 , то y(х) = C₁y₁(x) + C₂y₂(x) + … + C_ny_n(x) = , есть общее решение этого уровня. (4).

Из теоремы о неравенстве нулю вронскиана линейно-независимых решений ЛОДУ:

Если n решений y_1, y_2, … ,y_n ЛОДУ (2) и они линейно-независимы, на интервале (а,b) то определитель Вронского не может обращаться в ноль (0) ни в одной точке х ‌| для любого Х из (а,b) .

ð что (4) являются решением у ( n ) + P₁y ( n -1) +…+ P_n-1 y’ + P_n y = 0

остается доказать, что можно подобрать const-ты то С₁, С₂, … С_n , таким образом что функция (4) удовлетворяет любой системе начальных условий [н.у.]

Задаем н.у. , при x₀ (а,b) y(х₀) = y₀, y’(х₀) = y₀’, y ( n -1) (x₀) = y₀ ( n -1) определяем C_1,C₂,…, C_n

Определение:

Определителем этой системы является определитель Вронского

W[y_1, y_2, … ,y_n] 0, C_1,C₂,…, C_n — определяется един-м образом

Построим = C₁y₁(x) + C₂y₂(x) + … + C_ny_n(x) ,

согласно свойству (если y₁) α₁y₁ + α₂y₂ + …+ α_ny_n = 0 причем хотя бы одно h_i 0.

— является решением ДУ(2) = y(x) , т.к. система (5) определена теми же н.у., что и y(x) ч.т.д.

1) максимальное число линейно-независимых решение ЛОДУ, коэффициенты непрерывны на (a,b) равно порядку этого уравнения.

2) независимо от н.у. все другие решения таких уравнений ЛОДУ является линейной комбинацией этих независимых решений (решений ФС)

3) Пространство решений ЛОДУ n-го порядка имеет базис из n-векторов, т.е. пространство n-мерное.

4) Для решения ЛОДУ n-го порядка необходимо найти ФСР. Общее решение получается как линейная комбинация решений ФС.

11. Линейные однородные дифференциальные уравнения n-го порядка с постоянными коэффициентами. Вид частных решений, характеристическое уравнение(×)

ЛОДУ с постоянными коэффициентами

у ( n ) + P₁y ( n -1) +…+ P_n-1 y’ + P_n y = 0, где все P_i (i= 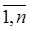)= const

будем искать частное решение y=e kx , к – неизвестная постоянная

y ( n ) =k ( n ) e kx

k (n) e kx + P₁k (n-1) e kx + … + P_ne kx = e kx (k (n) + P₁k (n-1) + … + P_n) = 0

e kx 0 => k (n) + P₁k (n-1) + … + P_n = 0, (1)

ð y=e kx — решение ДУ

(1) – характеристическое уравнение для ЛОДу с постоянными коэффициентами, выражения слева характеристический многочлен.

Решением характеристич уравнения (1) дает систему частных решений ЛОДу, структура ФСР зависит от вида корней характер уравнения.

(1) – алгебраическое уравнение n-ой степени, может иметь не более, чем n корней, обознач-м эти корни характеристического уравнения через k₁ ,k₂ …k_n

1)все корни хар-го уранения вещественны и различны

2)все корни различны, но среди них есть комплексные

3)среди действительных корней имеются кратные

4)среди комплексных корней есть кратные

Общий алгоритм решения ЛОДу с постоянным коэффициентом

1) составим характер уравнение : y=e kx , k ( n ) + P₁k ( n -1) + … + P_n = 0

2) найти корни характер уравнения k₁ ,k₂ …k_n

3) по характеру корней находим частное линейно-независимое решение по таблице 1

4) подставляем частное решение на основе Теоремы о структуре общего решения ЛОДУ и получаем общее решение y =

№	Вид корня	Соответственное решение
Действ корень кратности 1	e kx
Пара корней a bi;кратнос 1	e а x cosbx , e а x sinbx
Действит корень кратност α	e kx , хe kx , х 2 e kx , х 3 e kx ,…, х α-1 e kx
Пара сопряж корней α a bi	e а x cosbx , e а x sinbx хe а x cosbx , хe а x sinbx х 2 e а x cosbx , х 2 e а x sinbx х α-1 e а x cosbx , х α-1 e а x sinbx

13. Линейные неоднородные дифференциальные уравнения n-го порядка. Теорема о структуре общего решения (док. для n=2). Теорема о суперпозиции решений (док. для n=2).

у ( n ) + P₁y ( n -1) +…+ P_n-1 y’ + P_n y = f(x) (1) P_i – непрерывна на отрезке (a,b)

Теорема о структуре общего решения ЛНДУ

Общее решение ЛНДУ есть сумма частного решения и общего решения соответственного ему однородного уравнения

Для уравнения 2-го порядка ( но теорема применима для уравнений любого порядка)

Обозначим у*(х) – частное решение ЛНДУ

(х) – общее решение ЛОДУ

(2) у= у*+ — общее решение ЛНДУ

Дважды дифференцируем функцию (2) и подставляем у, y’,y” в (1’)

у*”(x) + ”(x) + P₁(x)[ у*(x)+ ’(x)] + P₂(x)[ у*(x)+ (x)] =

= [у*”(x)+ P₁(x) у*’(x)+ P₂(x) у*(x)] + [ ”(x) + P₁(x) ’ (x)+ P₂(x) (x)] = f(x) + 0 = 0

= C₁y₁(x) + C₂y₂(x), y_1,y₂ – частное решение ЛОДУ y” + P₁y’ + P₂ = 0

C₁C₂ – подбираем так, чтобы они удовлетворяли начальным условиям

y(x₀)=y₀ , y’(x₀)=y₀’, для любых х₀ (а,в), и любых y₀ ,y₀’

Линейная неоднородная система, определитель этой системы, определитель Вронского

W[y_1, y₂]≠0 =>система имеет единственное решение при любых ₀ , ’₀ ,y*_{0 ,}y*’₀ , это означает у= у*+ — общее решение ЛНДУ

Теорема2 принцип суперпозиции (принцип сложения решений)

Если функция y_i(x) является решением ЛНДУ

(3) y ( n ) + P₁y ( n -1) + … + P_ny = f_i(x) то функция = α₁y₁ + α₂y₂ + … + α_ny_n , то это функция является решением y ( n ) + P₁y ( n -1) + … + P_ny = α₁ f₁(x) + α₂ f₂(x) + … + α_n f_n(x) (4)

Подставим y, y’, y”, в (4) , учитываем что y₁ y₂ решение соответственного уравнения (3)

14. Линейные неоднородные дифференциальные уравнения n-го порядка с постоянными коэффициентами. Метод неопределенных коэффициентов для уравнений со специальной правой частью. Метод вариации произвольных постоянных (вывод рабочей формулы).

Рассмотрим ЛНДУ с постоянными коэф-ми.

Метод неопр-х коэф-в можно применять если правое ур-е имеет следующий вид: f(x)= , , -многочлены степени g и r соотв-но a и b некоторые числа. В основе метода неопр-х коэф-в лежит знание формы частного решения, а именно частное решение стоит искать в аналогич-ой форме свободного члена.

№	Вид правой части (f(x))	Корни харак-го уравнения	Вид частного решения y*
P (x)=A x +A x +… +A x+ A	а) число 0 не явл-ся корнем хар-го ур-я б) число 0 явл-ся корнем хар-го ур-я кратности	а) y*=b x +b x +…+ +b б) y*=x (B x +B x +… +B )
P (x)e = e ( A x + +A x +…+A x+ A ) p-действ-е число	а) число p не явл-ся корнем хар-го ур-я б) число p явл-ся корнем хар-го ур-я кратности	a) y*= e ( b x +b x +…+ +b ) б) y*= e x ( b x +b x +…+ +b )
P (x)cosgx+Q (x)singx g-число	а) число gi-не явл-ся корнем хар-го ур-я б) число gi-явл-ся корнем хар-го ур-я кратности	а) y*= (x)cosgx+ (x)singx б) y*=x ( (x)cosgx+ (x)singx)
P (x)e cosgx+ Q (x)e singx	а) число gi-не явл-ся корнем хар-го ур-я б) число gi-явл-ся корнем хар-го ур-я кратности	а) y*= (x) e cosgx+ (x)singx б) y*= x ( (x) e cosgx+ + (x)singx)

Замечание к таблице: 1)степени многоч-ов P и Q в случаях (3) и (4) можно считать одинаковыми, если они различны, то коэф-ты при недостающих степенях одного из многоч-ов можно считать=0.

2)правая часть ур-я может содержать несколько слагаемых; в этом случае сост-ся из неск-ких слагаемых в соотв-ии с Теоремой о неравенстве нулю вронскиана линейно-независимых решений ЛОДУ

Метод вариации производных постоянных(метод Лагранджа).

Метод позволяет найти решение ДУ независимо от вида правой части, когда известно общее решение соотв-го однородного ДУ.

Например: ДУ 2-го порядка. Пусть y”+P (x)y’+P (x)y=f(x) (1) пусть y (x) и y (x)-ФСРЛОДУ

y”+P (x)y’+P (x)y=0 (x)= C y (x)+C y (x) (2). Частное решение y*(x) в виде (14) считая при этом C и C не постоянными, а неизв-ми функциями от x.

y*= C (x)y (x)+C (x)y (x), y*= C’ (x)y (x)+C(x) y’ (x)+C’ (x)y (x)+ C(x) y’ (x)

Пусть C (x) и C (x) C’ (x)y (x)+ C’ (x)y (x)=0 /справедливое равенство (3), тогда y* ’= C (x)y’ (x)+ C (x)y’ (x); y* ”= C (x)y’ (x)+ C (x)y” (x)+ C’ (x)y’ (x)+ C (x)y” (x).

Подставим y*, y* ’, y* ” в (1): C (x)[ y” (x) + P (x)y ’(x) + P (x) y (x)] + C (x)[ y” (x) + P (x)y ’(x) + P (x) y (x)] + C’ (x)y’ (x)+ C’ (x)y’ (x)=f(x). Т.к. y (x), y (x) решения ОДУ, то выражения []=0 C’ (x)y’ (x) + C’ (x)y’ (x)=0.

Объясним два условия и (3):

C’ (x)y (x)+ C’ (x)y (x)=0

C’ (x)y’ (x)+ C’ (x)y’ (x)=f(x) (4)

Неопр-е ф-ии C’ (x) и C’ (x).

Определитель этой системы: W[y , y ]= 0 решая систему мы получим C (x)= (x),

C (x)= (x) проинтегрируем и получим решение C (x) и C (x) найдены. Подставим в y*.

Для ЛНДУ n-го порядка ф-ии C 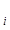(x) определяются из системы:

C’ (x)y + C’ (x)y +…+ C’ (x)y =0

C’ (x)y’ + C’ (x)y’ +…+ C’ (x)y’ =0

C’ (x)y + C’ (x)y +…+ C’ (x)y =0

C’ (x)y + C’ (x)y +…+ C’ (x)y =f(x)

Алгоритм решения ЛНДУ

1) найти ФСР однородного уравнения и записать его общее решение (ОУ)

2) записать частное решение неоднородного ДУ в форме общего решения ОУ считая C_i=C_i (x)

3) построить систему для определения C_i ‘(x) – решить ее

4) найти C_i (x) и подставить их в общее решение НДУ

Видео:ЛОДУ 2 порядка c постоянными коэффициентамиСкачать

Линейные дифференциальные уравнения высших порядков с постоянными коэффициентами

Ниже разберем способы, как решить линейные однородные и неоднородные дифференциальные уравнения порядка выше второго, имеющих постоянные коэффициенты. Подобные уравнения представлены записями y ( n ) + f n — 1 · y ( n — 1 ) + . . . + f 1 · y ‘ + f 0 · y = 0 и y ( n ) + f n — 1 · y ( n — 1 ) + . . . + f 1 · y ‘ + f 0 · y = f ( x ) , в которых f 0 , f 1 , . . . , f n — 1 — являются действительными числами, а функция f ( x ) является непрерывной на интервале интегрирования X .

Оговоримся, что аналитическое решение подобных уравнений иногда неосуществимо, тогда используются приближенные методы. Но, конечно, некоторые случаи дают возможность определить общее решение.

Видео:2185 ЛОДУ. Корни характеристического уравнения действительные и кратные.Скачать

Общее решение ЛОДУ и ЛДНУ

Мы зададим формулировку двух теорем, показывающих, какого вида общих решений ЛОДУ и ЛНДУ n -ого порядка следует искать.

Общим решением y 0 ЛОДУ y ( n ) + f n — 1 · y ( n — 1 ) + . . . + f 1 · y ‘ + f 0 · y = 0 на интервале
X (коэффициенты f 0 ( x ) , f 1 ( x ) , . . . , f n — 1 ( x ) непрерывны на X ) будет линейная комбинация
n линейно независимых частных решений ЛОДУ y j , j = 1 , 2 , . . . , n , содержащая произвольные постоянные коэффициенты C j , j = 1 , 2 , . . . , n , то есть y 0 = ∑ j = 1 n C j · y j .

Общим решением y ЛНДУ y ( n ) + f n — 1 · y ( n — 1 ) + . . . + f 1 · y ‘ + f 0 · y = f ( x ) на интервале X (коэффициенты f 0 ( x ) , f 1 ( x ) , . . . , f n — 1 ( x ) непрерывны на X ) и функцией f ( x ) будет являться сумма y = y 0 + y

, где y 0 — общее решение соответствующего ЛОДУ y ( n ) + f n — 1 · y ( n — 1 ) + . . . + f 1 · y ‘ + f 0 · y = 0 , а y

— некоторое частное решение исходного ЛНДУ.

Итак, общее решение линейного неоднородного дифференциального уравнения, содержащего постоянные коэффициенты y ( n ) + f n — 1 · y ( n — 1 ) + . . . + f 1 · y ‘ + f 0 · y = f ( x ) , нужно искать, как y = y 0 + y

— некоторое его частное решение, а y 0 = ∑ j = 1 n C j · y j – общее решение соответствующего однородного дифференциального уравнения y ( n ) + f n — 1 · y ( n — 1 ) + . . . + f 1 · y ‘ + f 0 · y = 0 .

В первую очередь рассмотрим, как осуществлять нахождение y 0 = ∑ j = 1 n C j · y j — общее решение ЛОДУ n -ого порядка с постоянными коэффициентами, а потом научимся определять частное решение y

линейного неоднородного дифференциального уравнения n -ого порядка при постоянных коэффициентах.

Алгебраическое уравнение n -ого порядка k n + f n — 1 · k n — 1 + . . . + f 1 · k + f 0 = 0 носит название характеристического уравнения линейного однородного дифференциального уравнения n -ого порядка, содержащего постоянные коэффициенты, записи y ( n ) + f n — 1 · y ( n — 1 ) + . . . + f 1 · y ‘ + f 0 · y = 0 .

Возможно определить n частных линейно независимых решений y 1 , y 2 , . . . , y n исходного ЛОДУ, исходя из значений найденных n корней характеристического уравнения k 1 , k 2 , . . . , k n .

Видео:2184 ЛОДУ. Корни характеристического уравнения действительные и различныеСкачать

Методы решения ЛОДУ и ЛНДУ

Укажем все существующие варианты и приведем примеры на каждый.

1. Когда все решения k 1 , k 2 , . . . , k n характеристического уравнения k n + f n — 1 · k n — 1 + . . . + f 1 · k + f 0 = 0 действительны и различны, линейно независимые частные решения будут выглядеть так:
   y 1 = e k 1 · x , y 2 = e k 2 · x , . . . , y n = e k n · x . Общее же решение ЛОДУ n -ого порядка при постоянных коэффициентах запишем как: y 0 = C 1 · e k 1 · x + C 2 · e k 2 · x + . . . + C n · e k n · x .

Пример 1

Задано ЛОДУ третьего порядка, содержащее постоянные коэффициенты y ‘ ‘ ‘ — 3 y » — y ‘ + 3 y = 0 . Определите его общее решение.

Решение

Cоставим характеристическое уравнение и найдем его корни, разложив предварительно многочлен из левой части равенства на множители, используя метод группировки:
k 3 — 3 k 2 — k + 3 = 0 k 2 ( k — 3 ) — ( k — 3 ) = 0 ( k 2 — 1 ) ( k — 3 ) = 0 k 1 = — 1 , k 2 = 1 , k 3 = 3

Ответ: найденные корни являются действительными и различными, значит общее решение ЛОДУ третьего порядка с постоянными коэффициентами запишем как: y 0 = C 1 · e — x + C 2 e x + C 3 · e 3 x .

1. Когда решения характеристического уравнения являются действительными и одинаковыми ( k 1 = k 2 = . . . = k n = k 0 ) , линейно независимые частные решения линейного однородного дифференциального уравнения n -ого порядка с постоянными коэффициентами буду иметь вид: y 1 = e k 0 · x , y 2 = x · e k 0 · x , . . . , y n = x n — 1 · e k 0 · x .

Общее же решение ЛОДУ будет выглядеть так:
y 0 = C 1 · e k 0 · x + C 2 · e k 0 · x + . . . + C n · x n — 1 · e k 0 · x = = e k 0 · x · C 1 + C 2 · x + . . . + C n · x n — 1

Задано дифференциальное уравнение: y ( 4 ) — 8 k ( 3 ) + 24 y » — 32 y ‘ + 16 y = 0 . Необходимо определить его общее решение.

Решение

Составим характеристическое уравнение заданного ЛОДУ: k 4 — 8 k 3 + 24 k 2 — 32 k + 16 = 0 .

Преобразуем данное характеристическое уравнение, используя формулу бинома Ньютона, оно примет вид: k — 2 4 = 0 . Отсюда мы выделим его четырехкратный корень k 0 = 2 .

Ответ: общим решением заданного ЛОДУ станет: y 0 = e 2 x · C 1 + C 2 · x + C 3 · x 2 + C 4 · x 3

1. Когда решения характеристического уравнения линейного однородного дифференциального уравнения n -ого порядка при постоянных коэффициентах — различные комплексно сопряженные пары α 1 ± i · β 1 , α 2 ± i · β 2 , . . . , α m ± i · β m , n = 2 m , линейно независимые частные решения такого ЛОДУ будут иметь вид:
   y 1 = e α 1 x · cos β 1 x , y 2 = e α 1 x · sin β 1 x , y 3 = e α 2 x · cos β 2 x , y 4 = e α 2 x · sin β 2 x , … y n — 1 = e α m x · cos β m x , y n = e α m x · sin β m x

Общее же решение запишем так:

y 0 = e α 1 x · C 1 · cos β 1 x + C 2 · sin β 1 x + + e α 2 x · C 3 · cos β 2 x + C 4 · sin β 2 x + . . . + + e α m x · C n — 1 · cos β m x + C n · sin β m x

Задано ЛОДУ четвертого порядка при постоянных коэффициентах y ( 4 ) — 6 y ( 3 ) + 14 y » — 6 y ‘ + 13 y = 0 . Необходимо его проинтегрировать.

Решение

Составим характеристическое уравнение заданного ЛОДУ: k 4 — 6 k 3 + 14 k 2 — 6 k + 13 = 0 . Осуществим преобразования и группировки:

k 4 — 6 k 3 + 14 k 2 — 6 k + 13 = 0 k 4 + k 2 — 6 k 3 + k + 13 k 2 + 1 = 0 k 2 + 1 k 2 — 6 k + 13 = 0

Из полученного результата несложно записать две пары комплексно сопряженных корней k 1 , 2 = ± i и k 3 , 4 = 3 ± 2 · i .

Ответ: общее решение заданного линейного однородного дифференциального уравнения n -ого порядка с постоянными коэффициентами запишется как:
y 0 = e 0 · C 1 · cos x + C 2 · sin x + e 3 x · C 3 · cos 2 x + C 4 · sin 2 x = = C 1 · cos x + C 2 · sin x + e 3 x · C 3 · cos 2 x + C 4 · sin 2 x

1. Когда решения характеристического уравнения — это совпадающие комплексно сопряженные пары α ± i · β , линейно независимыми частными решениями линейного однородного дифференциального уравнения n-ого порядка с постоянными коэффициентами будут записи:
   y 1 = e α · x · cos β x , y 2 = e α · x · sin β x , y 3 = e α · x · x · cos β x , y 4 = e α · x · x · sin β x , … y n — 1 = e α · x · x m — 1 · cos β x , y n = e α · x · x m — 1 · sin β x

Общим решением ЛОДУ будет:

y 0 = e α · x · C 1 · cos β x + C 2 · sin β x + + e α · x · x · C 4 · cos β x + C 3 · sin β x + . . . + + e α · x · x m — 1 · C n — 1 · cos β x + C n · sin β x = = e α · x · cos β x · C 1 + C 3 · x + . . . + C n — 1 · x m — 1 + + e α · x · sin β x · C 2 + C 4 · x + . . . + C n · x m — 1

Задано линейное однородное дифференциальное уравнение с постоянными коэффициентами y ( 4 ) — 4 y ( 3 ) + 14 y » — 20 y ‘ + 25 y = 0 . Необходимо определить его общее решение.

Решение

Составим запись характеристического уравнения, заданного ЛОДУ, и определим его корни:

k 4 — 4 k 3 + 14 k 2 — 20 k + 25 = 0 k 4 — 4 k 3 + 4 k 2 + 10 k 2 — 20 k + 25 = 0 ( k 2 — 2 k ) 2 + 10 ( k 2 — 2 k ) + 25 = 0 ( k 2 — 2 k + 5 ) 2 = 0 D = — 2 2 — 4 · 1 · 5 = — 16 k 1 , 2 = k 3 , 4 = 2 ± — 16 2 = 1 ± 2 · i

Таким образом, решением характеристического уравнения будет двукратная комплексно сопряженная пара α ± β · i = 1 ± 2 · i .

Ответ: общее решение заданного ЛОДУ: y 0 = e x · cos 2 x · ( C 1 + C 3 · x ) + e x · sin 2 x · ( C 2 + C 4 · x )

1. Встречаются различные комбинации указанных случаев: некоторые корни характеристического уравнения ЛОДУ n -ого порядка с постоянными коэффициентами являются действительными и различными, некоторые — действительными и совпадающими, а какие-то — комплексно сопряженными парами или совпадающими комплексно сопряженными парами.

Пример 5

Задано дифференциальное уравнение y ( 5 ) — 9 y ( 4 ) + 41 ( 3 ) + 35 y » — 424 y ‘ + 492 y = 0 . Необходимо определить его общее решение.

Решение

Составим характеристическое уравнение заданного ЛОДУ: k 5 — 9 k 4 + 41 k 3 + 35 k 2 — 424 k + 492 = 0 .

Левая часть содержит многочлен, который возможно разложить на множители. В числе делителей свободного члена определяем двукратный корень k 1 = k 2 = 2 и корень k 3 = — 3 .

На основе схемы Горнера получим разложение: k 5 — 9 k 4 + 41 k 3 + 35 k 2 — 424 k + 492 = k + 3 k — 2 2 k 2 — 8 k + 41 .

Квадратное уравнение k 2 — 8 k + 41 = 0 дает нам оставшиеся корни k 4 , 5 = 4 ± 5 · i .

Ответ: общим решением заданного ЛОДУ с постоянными коэффициентами будет: y 0 = e 2 x · C 1 + C 2 x + C 3 · e — 3 x + e 4 x · C 4 · cos 5 x + C 5 · sin 5 x

Таким образом, мы рассмотрели основные случаи, когда возможно определить y 0 — общее решение ЛОДУ n -ого порядка с постоянными коэффициентами.

Следующее, что мы разберем – это ответ на вопрос, как решить линейное неоднородное дифференциальное уравнение n -ого порядка с постоянными коэффициентами записи y ( n ) + f n — 1 · y ( n — 1 ) + . . . + f 1 · y ‘ + f 0 · y = f ( x ) .

Общее решение в таком случае составляется как сумма общего решения соответствующего ЛОДУ и частного решения исходного ЛНДУ: y = y 0 + y

. Поскольку мы уже умеем определять y 0 , остается разобраться с нахождением y

, т.е. частного решения ЛНДУ порядка n с постоянными коэффициентами.

Приведем все способы нахождения y

согласно тому, какой вид имеет функция f ( x ) , находящаяся в правой части рассматриваемого ЛНДУ.

Когда f ( x ) представлена в виде многочлена n -ой степени f ( x ) = P n ( x ) , частным решением ЛНДУ станет: y

= Q n ( x ) · x γ . Здесь Q n ( x ) является многочленом степени n , а r – указывает, сколько корней характеристического уравнения равно нулю.
Когда функция f ( x ) представлена в виде произведения многочлена степени n и экспоненты f ( x ) = P n ( x ) · e α · x , частным решением ЛНДУ второго порядка станет: y

= e α · x · Q n ( x ) · x γ . Здесь Q n ( x ) является многочленом n —ой степени, r указывает, сколько корней характеристического уравнения равно α .
Когда функция f ( x ) записана как f ( x ) = A 1 cos ( β x ) + B 1 sin ( β x ) , где А 1 и В 1 – числа, частным решением ЛНДУ станет запись y

= A cos β x + B sin β x · x γ . Здесь где А и В являются неопределенными коэффициентами, r – указывает, сколько комплексно сопряженных пар корней характеристического уравнения равно ± i β .
Когда f ( x ) = e α x · P n ( x ) sin β x + Q k x cos β x , то y

= e α x · L m x sin β x + N m x cos β x · x γ , где r – указывает, сколько комплексно сопряженных пар корней характеристического уравнения равно α ± i β , P n ( x ) , Q k ( x ) , L m ( x ) и N m ( x ) являются многочленами степени n , k , m и m соответственно, m = m a x ( n , k ) .

Коэффициенты, которые неизвестны, определяются из равенства y

( n — 1 ) + . . . + f 1 y

Подробности нахождения решений уравнений в каждом из указанных случаев можно изучить в статье линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами, поскольку схемы решения ЛНДУ степени выше второй полностью совпадают.

Когда функция f ( x ) имеет любой иной вид, общее решение ЛНДУ возможно определить, используя метод вариации произвольных постоянных. Его разберем подробнее.

Пусть нам заданы y j , j = 1 , 2 , . . . , n — n линейно независимые частные решения соответствующего ЛОДУ, тогда, используя различные вариации произвольных постоянных, общим решением ЛНДУ
n -ого порядка с постоянными коэффициентами будет запись: н = ∑ j = 1 n C j ( x ) · y j . В нахождении производных функций C j ( x ) , j = 1 , 2 , . . . , n поможет система уравнений:

∑ j = 1 n C j ‘ ( x ) · y j = 0 ∑ j = 1 n C j ‘ ( x ) · y ‘ j = 0 ∑ j = 1 n C j ‘ ( x ) · y » j = 0 … ∑ j = 1 n C j ‘ ( x ) · y j ( n — 2 ) = 0 ∑ j = 1 n C j ‘ ( x ) · y j ( n — 1 ) = 0

а собственно функции C j ( x ) , j = 1 , 2 , . . . , n найдем при последующем интегрировании.

Задано ЛНДУ с постоянными коэффициентами: y ‘ ‘ ‘ — 5 y » + 6 y ‘ = 2 x . Необходимо найти его общее решение.

Решение

Составим характеристическое уравнение: k 3 — 5 k 2 + 6 k = 0 . Корни данного уравнения: k 1 = 0 , k 2 = 2 и k 3 = 3 . Таким образом, общим решением ЛОДУ будет запись: y 0 = C 1 + C 2 · e 2 x + C 3 · e 3 x , а частные линейно независимые решения это: y 1 = 1 , y 2 = e 2 x , y 3 = e 3 x .

Варьируем произвольные постоянные: y = C 1 ( x ) + C 2 ( x ) · e 2 x + C 3 ( x ) · e 3 x .

Чтобы определить C 1 ( x ) , C 2 ( x ) и C 3 ( x ) , составим систему уравнений:

C ‘ 1 ( x ) · y 1 + C ‘ 2 ( x ) · y 2 + C ‘ 3 ( x ) · y 3 = 0 C ‘ 1 ( x ) · y ‘ 1 + C ‘ 2 ( x ) · y ‘ 2 + C ‘ 3 ( x ) · y ‘ 3 = 0 C ‘ 1 ( x ) · y » 1 + C ‘ 2 ( x ) · y » 2 + C ‘ 3 ( x ) · y » 3 = 2 x ⇔ C ‘ 1 ( x ) · 1 + C ‘ 2 x · e 2 x ‘ + C ‘ 3 ( x ) · y 3 = 0 C ‘ 1 ( x ) · 1 ‘ + C ‘ 2 x · e 2 x ‘ + C ‘ 3 ( x ) · e 3 x ‘ = 0 C ‘ 1 ( x ) · 1 ‘ ‘ + C ‘ 2 x · e 2 x ‘ ‘ + C ‘ 3 ( x ) · e 3 x ‘ ‘ = 2 x ⇔ C ‘ 1 ( x ) · 1 + C ‘ 2 x · e 2 x + C ‘ 3 ( x ) · e 3 x = 0 C ‘ 1 ( x ) · 0 + C ‘ 2 ( x ) · 2 e 2 x + C ‘ 3 ( x ) · 3 e 3 x = 0 C ‘ 1 ( x ) · 0 + C ‘ 2 ( x ) · 4 e 2 x + C ‘ 3 ( x ) · 9 e 3 x = 2 x

Решаем, используя метод Крамера:

∆ = 1 e 2 x e 3 x 0 2 e 2 x 3 e 3 x 0 4 e 2 x 9 e 3 x = 18 e 2 x · e 3 x — 12 e 2 x · e 3 x = 6 e 5 x ∆ C 1 ‘ ( x ) = 0 e 2 x e 3 x 0 2 e 2 x 3 e 3 x 2 x 4 e 2 x 9 e 3 x = e 5 x · 2 x ⇒ C ‘ 1 ( x ) = ∆ C 1 ‘ ( x ) ∆ = e 5 x · 2 x 6 e 5 x = 1 6 · 2 x ∆ C 2 ‘ ( x ) = 1 0 e 3 x 0 0 3 e 3 x 0 2 x 9 e 3 x = — 3 e x · 2 x ⇒ C ‘ 2 ( x ) = ∆ C 2 ‘ ( x ) ∆ = — 3 e 3 x · 2 x 6 e 5 x = — 1 2 · e — 2 x · 2 x ∆ C 3 ‘ ( x ) = 1 e 2 x 0 0 2 e 2 x 0 0 4 e 2 x 2 x = 2 e 2 x · 2 x ⇒ C ‘ 3 ( x ) = ∆ C 3 ‘ ( x ) ∆ = 2 e 2 x · 2 x 6 e 5 x = 1 3 · e — 3 x · 2 x

Интегрируем C ‘ 1 ( x ) = 1 6 · 2 x с помощью таблицы первообразных, а
C ‘ 2 ( x ) = — 1 2 · e — 2 x · 2 x и C ‘ 3 ( x ) = 1 3 · e — 3 x · 2 x при помощи метода интегрирования по частям, получим:
C 1 ( x ) = 1 6 · ∫ 2 x d x = 1 6 · 2 x ln 2 + C 4 C 2 ( x ) = — 1 2 · ∫ e — 2 x · 2 x d x = — 1 2 · e — 2 x · 2 x ln 2 — 2 + C 5 C 3 ( x ) = 1 3 · ∫ e — 3 x · 2 x d x = 1 3 · e — 3 x · 2 x ln 2 — 3 + C 6

Ответ: искомым общим решением заданного ЛОДУ с постоянными коэффициентами будет:

y = C 1 ( x ) + C 2 ( x ) · e 2 x + C 3 ( x ) · e 3 x = = 1 6 · 2 x ln 2 + C 4 + — 1 2 · e — 2 x · 2 x ln 2 — 2 + C 5 · e 2 x + + 1 3 · e — 3 x · 2 x ln 2 — 3 + C 6 · e 3 x

где C 4 , C 5 и C 6 – произвольные постоянные.

Видео:2194. ЛОДУ. Корни характеристического уравнения комплексные и действительные.Скачать

Фср и общее решение лоду в случае кратных действительных корней характеристического уравнения

Для линейного однородного дифференциального уравнения n-го порядка

Совокупность n линейно независимых решений линейного однородного дифференциального уравнения n-го порядка y₁(x), y₂(x), . y_n(x) называется фундаментальной системой решений уравнения.

Для линейного однородного дифференциального уравнения с постоянными коэффициентами существует простой алгоритм построения фундаментальной системы решений. Будем искать решение уравнения в виде y(x) = exp(lx):
exp(lx) (n) + a₁exp(lx) (n-1) + . + a_n-1exp(lx)’ + a_nexp(lx)=
= (l n + a₁l n-1 + . + a_n-1l + a_n)exp(lx) = 0,
т.е. число l является корнем характеристического уравнения
l n + a₁l n-1 + . + a_n-1l + a_n = 0.
Левая часть характеристического уравнения называется характеристическим многочленом линейного дифференциального уравнения:
P(l) = l n + a₁l n-1 + . + a_n-1l + a_n.
Таким образом, задача о решении линейного однородного уравнения n -го порядка с постоянными коэффициентами сводится к решению алгебраического уравнения.

ПРИМЕР 1. Фундаментальная система решений и общее решение для случая простых действительных корней.

ПРИМЕР 2. Фундаментальная система решений и общее решение для случая кратных действительных корней.

ПРИМЕР 3. Фундаментальная система решений и общее решение для случая п простых комплексных корней.

ПРИМЕР 4. Фундаментальная система решений и общее решение для случая простых комплексных корней. Мнимые корни.

ПРИМЕР 5. Фундаментальная система решений и общее решение для случая кратных комплексных корней.

ПРИМЕР 6. Решение задачи Коши.

Исправляем ошибки: Нашли опечатку? Выделите ее мышкой и нажмите Ctrl+Enter

🎦 Видео

2191. ЛОДУ. Корни характеристического уравнения комплексные, не кратные.Скачать

2187. ЛОДУ. Корни характеристического уравнения действительные, не кратные.Скачать

ФСР. Система однородных уравнений. Общее решениеСкачать

Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентамиСкачать

15. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентамиСкачать

16. Линейные неоднородные дифференциальные уравнения 2-го порядка с постоянными коэффициентамиСкачать

Характеристическое уравнение в ДУСкачать

Линейное однородное дифференциальное уравнение 2-го порядка с постоянными коэффициентами.Скачать

2214 ЛНДУ. Правая часть - многочлен, среди корней характеристического уравнения нет нулей.Скачать

15. Однородная система линейных уравнений / фундаментальная система решенийСкачать

Линейное неоднородное дифференциальное уравнение с постоянными коэффициентами 4y''-y=x^3-24x #1Скачать

ЛНДУ II п. со спец. правой ч. (sin, cos)Скачать

Задача Коши ➜ Частное решение линейного однородного дифференциального уравненияСкачать

Решение системы дифференциальных уравнений методом ЭйлераСкачать

Решение линейного однородного дифференциального уравнения. Практическая часть. 11 класс.Скачать