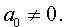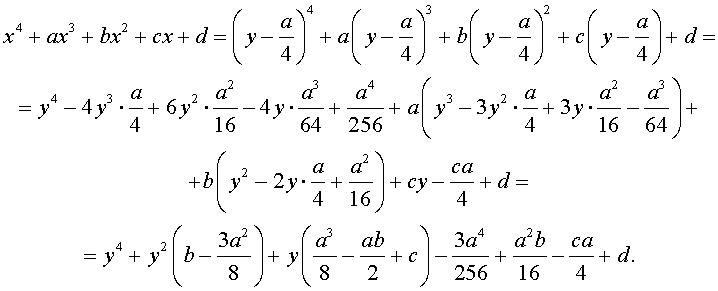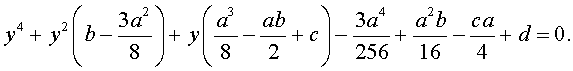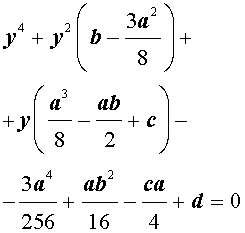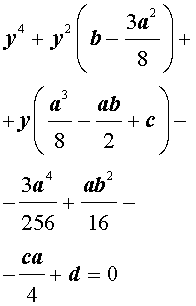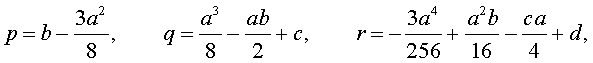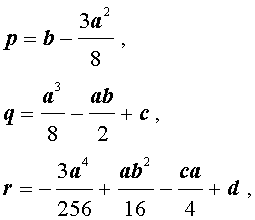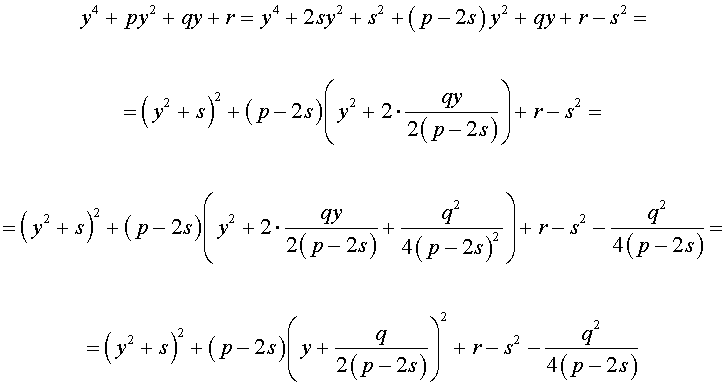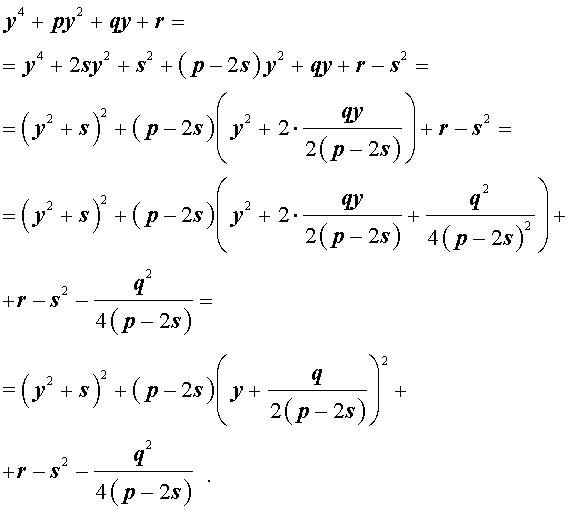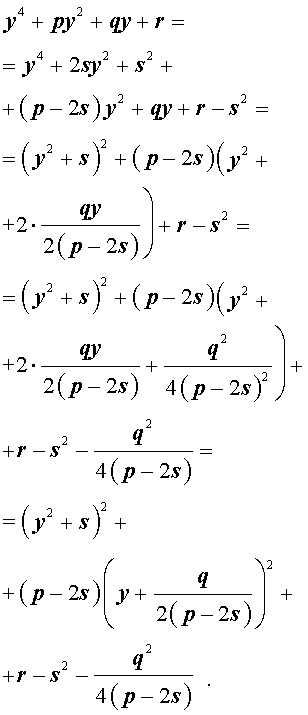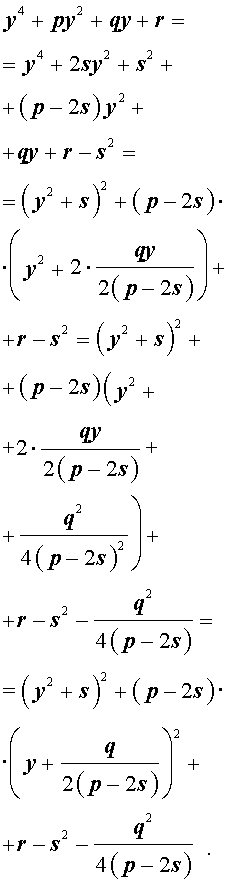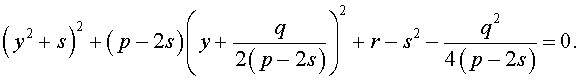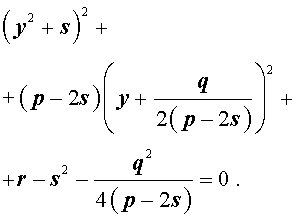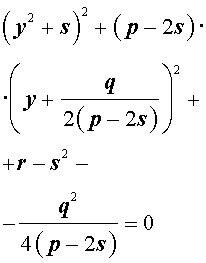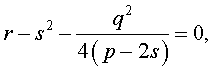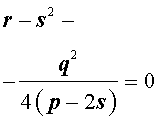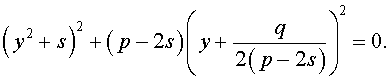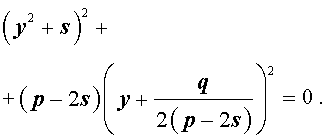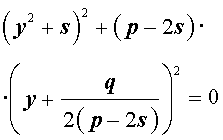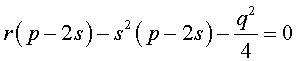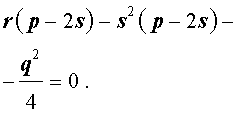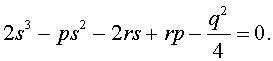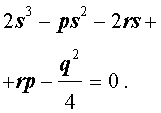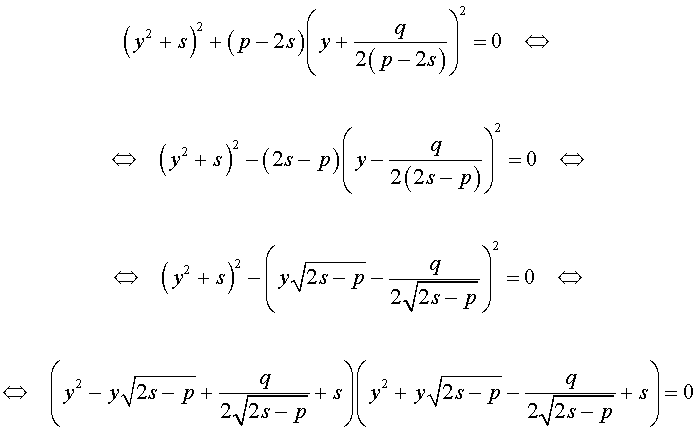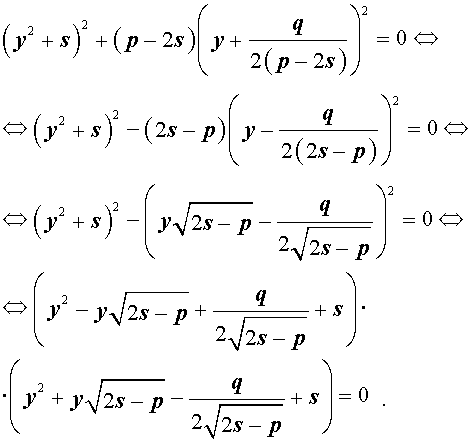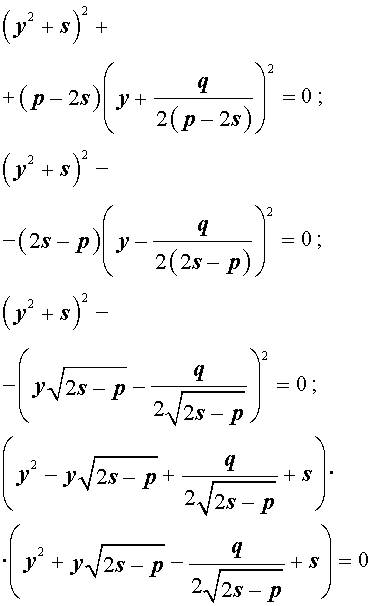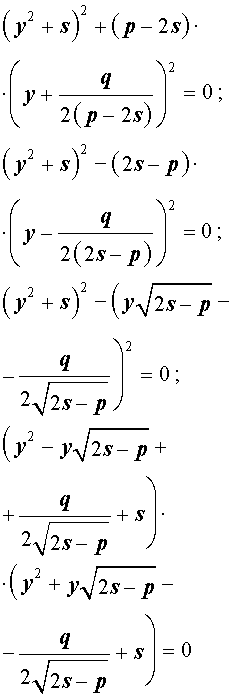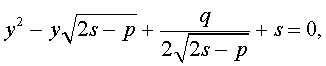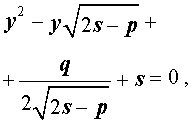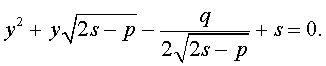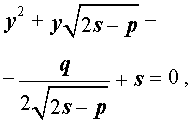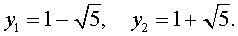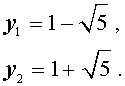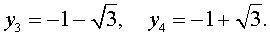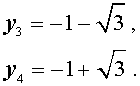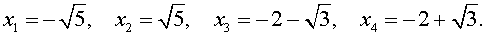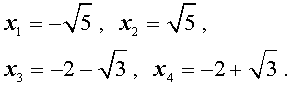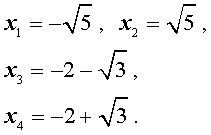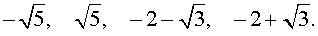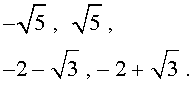Схема метода Феррари Схема метода Феррари |
 Приведение уравнений 4-ой степени Приведение уравнений 4-ой степени |
 Разложение на множители. Кубическая резольвента Разложение на множители. Кубическая резольвента |
 Пример решения уравнения 4-ой степени Пример решения уравнения 4-ой степени |
- Схема метода Феррари
- Приведение уравнений 4-ой степени
- Разложение на множители. Кубическая резольвента
- Пример решения уравнения 4-ой степени
- Скандал давно минувших дней
- «Великое искусство»
- Дель Ферро, Фиоре и Тарталья
- Поединок
- Кардано
- Четвёртая степень
- Комплексные числа и их приложение к решению уравнений третьей и четвертой степени (стр. 5 )
- Занятие 16. Решение уравнений четвертой степени методом Феррари
- 📽️ Видео
Видео:✓ Как решать кубические уравнения. Формула Кардано | Ботай со мной #025 | Борис ТрушинСкачать

Схема метода Феррари
Целью данного раздела является изложение метода Феррари , с помощью которого можно решать уравнения четвёртой степени
| a0x 4 + a1x 3 + a2x 2 + + a3x + a4 = 0, | (1) |
где a0, a1, a2, a3, a4 – произвольные вещественные числа, причем
Метод Феррари состоит из двух этапов.
На первом этапе уравнения вида (1) приводятся к уравнениям четвертой степени, у которых отсутствует член с третьей степенью неизвестного.
На втором этапе полученные уравнения решаются при помощи разложения на множители, однако для того, чтобы найти требуемое разложение на множители, приходится решать кубические уравнения.
Видео:Как решать уравнения четвёртой степени. Формула Феррари | #БотайСоМной #026 | Борис ТрушинСкачать

Приведение уравнений 4-ой степени
Разделим уравнение (1) на старший коэффициент a0 . Тогда оно примет вид
| x 4 + ax 3 + bx 2 + + cx + d = 0, | (2) |
где a, b, c, d – произвольные вещественные числа.
Сделаем в уравнении (2) замену
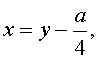 | (3) |
где y – новая переменная.
то уравнение (2) принимает вид
В результате уравнение (2) принимает вид
Если ввести обозначения
то уравнение (4) примет вид
| y 4 + py 2 + qy + r = 0, | (5) |
где p, q, r – вещественные числа.
Первый этап метода Феррари завершён.
Видео:Уравнения 3 и 4 степени. Методы Кардано и Феррари. ПродолжениеСкачать

Разложение на множители. Кубическая резольвента
Добавив и вычитая в левой части уравнения (5) выражение
где s – некоторое число, которое мы определим чуть позже, из (5) получим
Следовательно, уравнение (5) принимает вид
Если теперь выбрать число s так, чтобы оно являлось каким-нибудь решением уравнения
то уравнение (6) примет вид
Избавляясь от знаменателя, уравнение (7) можно переписать в виде
или, раскрыв скобки, — в виде
Полученное кубическое уравнение (9), эквивалентное уравнению (7), называют кубической резольвентой уравнения 4-ой степени (5).
Если какое-нибудь решение кубической резольвенты (9) найдено, то уравнение (8) можно решить, разложив его левую часть на множители с помощью формулы сокращенного умножения «Разность квадратов».
Таким образом, для решения уравнения (8) остаётся решить квадратное уравнение
а также квадратное уравнение
Вывод метода Феррари завершен.
Видео:Уравнение четвертой степениСкачать

Пример решения уравнения 4-ой степени
Пример . Решить уравнение
| x 4 + 4x 3 – 4x 2 – – 20x – 5 = 0. | (12) |
Решение . В соответствии с (3) сделаем в уравнении (12) замену
| x = y – 1. | (13) |
то в результате замены (13) уравнение (12) принимает вид
| y 4 – 10y 2 – 4y + 8 = 0. | (14) |
В соответствии с (5) для коэффициентов уравнения (14) справедливы равенства
| p = – 10, q = – 4, r = 8. | (15) |
В силу (9) и (15) кубической резольвентой для уравнения (14) служит уравнение
которое при сокращении на 2 принимает вид:
| s 3 + 5s 2 – 8s – 42 = 0. | (16) |
| s = – 3. | (17) |
Подставляя значения (15) и (17) в формулу (10), получаем уравнение
Подставляя значения (15) и (17) в формулу (11), получаем уравнение
В завершение, воспользовавшись формулой (13), из (18) и (19) находим корни уравнения (12):
Замечание . При решении примера мы попутно получили разложение левой части уравнения (14) на множители:
| y 4 – 10y 2 – 4y + 8 = = (y 2 – 2y – 4) (y 2 + + 2y – 2). | (20) |
Предоставляем посетителю нашего сайта возможность убедиться в справедливости равенства (19) в качестве несложного упражнения.
Видео:Решение уравнений третьей степени (формула Кардано)Скачать

Скандал давно минувших дней
Ни одно научное открытие не носит имени своего истинного автора.
Принцип Арнольда (открыт С. Стиглером)
Джероламо Кардано (1501–1576)
Как-то в редакции одного математического журнала за чашкой чая зашёл разговор о справедливости в науке. Вспомнили, что «кольца Ньютона» открыл Гук, «преобразования Лоренца» первым выполнил Фитцджеральд, в Америке за 500 лет до Колумба побывал Эйрик Рыжий, а ещё за 100 лет до него — Гунбьёрн. В математике Гаусс разработал «неевклидову геометрию» до Лобачевского, Бойяи и Римана, «формулами Виета» пользовались ещё до его рождения.
– И «формулу Кардано» для решения кубического уравнения сам Кардано попросту украл у Тартальи, — припомнил кто-то.
«Великое искусство»
В 1545 году из-под пера Джероламо Кардано вышла книга «Великое искусство» (Ars magna), собравшая все новейшие достижения в математике к середине XVI века. И сразу разразился скандал.
Но сначала немного истории.
Мрачное средневековье погрузило европейскую науку, в том числе и математику, в спячку на тысячу лет. Труды греческих учёных оказались никому не нужными, и про них попросту забыли. Конечно, купцы привозили отрывочные сведения о достижениях арабских математиков, но это купцы, их интересовала арифметика. Однако жизнь продолжалась, экономика развивалась, и ей потребовались научные и технические достижения.
Математика сдвинулась с «мёртвой точки». Даже стали проводиться математические состязания, некое подобие дуэлей. Два математика посылали друг другу определённое число задач, кто больше решит, тот и победитель. И этот победитель не только получал звание великого математика, но и вполне мог занять весьма привлекательное в материальном отношении место математика при дворе герцога, короля, а то и самого Папы Римского. Так что сражаться было за что.
Загубить науку можно быстро, буквально в течение жизни одного поколения. А для восстановления науки требуются столетия. И в XVI веке европейские математики только осваивали наследие древних греков, индусов и арабов. Рецепты решения квадратных уравнений определённого вида встречались ещё в древнем Вавилоне. Евклид в некоторых задачах на построение фактически решал квадратные уравнения. Умели их решать и арабские математики. Правда, решали они их при помощи геометрических построений, но зато получали правильные ответы. Кубические уравнения решать никто не умел.
И вот в книге Кардано появились общие формулы корней кубического уравнения! Сенсация! Греки остались позади! Но откуда взялся скандал?
Дель Ферро, Фиоре и Тарталья
Первым справился с решением кубического уравнения вида x 3 + ax = b профессор математики из Болонского университета Сципион дель Ферро. Перед смертью в 1526 году он поделился своей находкой с учениками. Один из них, некий Антонио Фиоре, попытался при помощи этого подарка стать непобедимым в поединках математиков. И в конце 1534 года он послал Никколо Тарталье вызов на состязание по решению задач.

Никколо Фонтана Тарталья (1499/1500–1557), итальянский математик. Перевёл на итальянский «Начала» Евклида и сделал комментарий к ним. Изучал баллистику
Никколо родился около 1500 года. Ещё в детстве он получил ранение горла, говорил с трудом, за что и получил прозвище Тарталья, что значит «заика». Бедная семья не могла оплатить учёбу сына в школе, но мальчик упорно постигал сам все науки, в том числе и математику. К моменту описываемых событий он уже получил известность и за пределами родной Брешии.
Поединок
Фиоре предложил Тарталье тридцать задач, и каждая была связана с необходимостью решения уравнения третьей степени. В то время такие задачи считались неразрешимыми в общем случае. Поэтому почти до конца срока Тарталья даже не пытался их решать: он собирался обличить противника в том, что тот дал ему задачи, с которыми сам не может справиться. Но тут до Тартальи дошли слухи, что у Фиоре есть способ решать такие уравнения. Приложив огромные усилия, Тарталья и сам нашёл такой способ, быстро расправился со всеми тридцатью задачами и отправил свои записи нотариусу, исполнявшему роль судьи.
Что же касается Фиоре, то он не смог решить ни одной задачи, предложенной ему Тартальей. Более того, он не смог решить и ни одной своей задачи, хотя владел методом дель Ферро. И это ещё раз доказывает необходимость регулярных занятий и тренировок. Любой человек знает, что забить гвоздь можно, если приставить его острым концом к доске и ударить молотком. Знать-то он знает, но научится грамотно забивать только после того, как погнёт тысячу гвоздей и сотню раз попадёт по пальцам — естественно, по своим.
К математике подобное утверждение относится в гораздо большей степени. Фиоре, получив от дель Ферро готовый рецепт нахождения корней кубического уравнения, не сомневался, что теперь-то он справится с любой задачей, и поэтому не утруждал себя подготовкой к состязанию. А вот Тарталья сам решил кубическое уравнение в общем виде, получил прекрасную практику обращения с такими уравнениями, поэтому и одолел все задачи за несколько дней.
И вот ирония судьбы. Формула корня кубического уравнения, открытая дель Ферро и независимо от него Тартальей, носит имя Кардано. Так в чём же дело?
В то время уравнения записывали не так, как мы привыкли. Например, уравнение x 3 + 5x = 12 Кардано записал бы так:
I. cubus p. 5. positionibus aequаntur I2
Здесь «I» — единица, «cubus» — куб неизвестной, «p.» — знак «+», «positionibus» — неизвестная, «aequаntur» — равно. Скобки и знак равенства ещё не использовались, знак корня записывался как 
Кардано
Цель, к которой я стремился, заключалась в увековечении моего имени.
Вращающееся тело, закреплённое на кардановом подвесе. Даже если внешнее кольцо меняет своё положение в пространстве, ось вращения не меняется. Это наблюдение используется в гироскопах
Джероламо Кардано родился в 1501 году. Получив прекрасное образование, он проявил себя во многих областях деятельности. Знаменитый врач, успешно лечивший важных особ. Талантливый инженер, предложивший для кареты испанского короля Карла V подвеску, чтобы карета Его Величества не наклонялась на неровных дорогах, оставаясь горизонтальной (сегодня мы такой подвес называем кардановым). Физик, экспериментально измеривший отношение плотности воздуха к плотности воды. Правда, немного ошибся, но кто и сейчас сможет померить точнее теми же приборами? Азартный игрок, заложивший основы теории вероятностей.
Карданный вал позволяет передать вращение между непараллельными осями. Он используется в большинстве автомобилей
А ещё Кардано занимался математикой. Он долго уговаривал Тарталью открыть ему секрет решения кубических уравнений, чтобы украсить им книгу «Великое искусство». Своё желание он аргументировал так: никто больше не станет состязаться с Тартальей в решении задач, потому что он умеет решать кубические уравнения, а другие не умеют. Под влиянием ли этого, вполне убедительного, аргумента или по какой-то другой причине, но Тарталья в конце концов уступил. Только поставил при этом условие, что Кардано не будет публиковать его открытие без разрешения самого Тартальи.
Кардано согласился. Но когда один из учеников дель Ферро поделился с ним рецептом своего учителя, Кардано счёл себя свободным от обязательств, выданных им Тарталье, и опубликовал способ решения кубического уравнения. Так появилась «формула Кардано», хотя сам Кардано не скрывал приоритета дель Ферро и Тартальи.
И сейчас, пять веков спустя, вряд ли кто-нибудь сможет до конца разобраться в этой воистину детективной истории.
Это формула Кардано для одного из решений уравнения x 3 + ax = b, где a, b > 0. В случае
уравнение имеет три решения, но формулу просто применить нельзя: нужно извлекать квадратный корень из отрицательного числа. Позже с помощью комплексных чисел удалось придать смысл квадратному корню из отрицательного числа, и применение формулы стало возможным даже в этом случае. При этом решения, вычисленные по формуле, получаются действительными.
Четвёртая степень
Без упоминания Феррари, Абеля и Галуа рассказ об истории решения кубических уравнений был бы неполным.
Полторы тысячи лет математики не могли подступиться к кубическому уравнению, но стоило его решить, как буквально тут же было решено в общем виде и уравнение четвёртой степени. Сделал это ученик Кардано Луиджи Феррари. Любопытно, что для решения этого уравнения требуется «по пути» решить вспомогательное уравнение третьей степени.
Все попытки решить в общем виде уравнение пятой степени в следующие три века успехом не увенчались. И вот в 1826 году норвежский математик Нильс Абель доказал, что общей формулы для решения уравнений пятой степени не существует, и для уравнений более высоких степеней — тоже. Своё открытие Абель сделал в 24 года, но прожил огорчительно мало, всего 27 лет.
Ещё меньше, неполный 21 год, прожил гениальный французский математик Эварист Галуа. Он продолжил исследования Абеля, определив, как по виду алгебраического уравнения узнать, решается ли оно. Метод, предложенный Галуа, положил начало фундаментальному разделу математики — теории групп. Название «группа» предложил сам Галуа. Погиб он на дуэли. В ночь перед дуэлью Галуа изложил на бумаге свои мысли о математике. Разобраться в этих записках и понять идеи Галуа математики смогли только через много десятилетий.
И ещё важная деталь. Решение уравнения третьей степени привело математиков к необходимости заняться комплексными числами. Функции комплексного переменного играют немалую роль в современной теоретической физике и электротехнике, не говоря уже о самой математике.
Опять голословные наезды на средневековье. К которому, между прочим, Тартьлья и относится.
В Средневековье — примерно на границе Раннего и Высокого — европейцы изобрели перо и получили от азиатов бумагу, что позволило им гораздо проще и больше писать. Просто грамотные средневековые европейцы, в отличие от грамотных жителей античности, жили не в городах, а на дачах, и писать на камнях не привыкли, так что текстов тех времён до нас дошло мало. А писали они много что: рассчитывали пасхалии (например, Беда — в VIII веке), создавали финансовую систему, намного превосходящую бытовые представления о финансах у наших современников (понятно, что современная финансовая система ещё сложнее, но обычный, скажем, физик или математик всё равно не разбирается в ней даже в том объёме, в котором банкиры работали в XIV веке). Придумали многопольную систему и мельницы. И школы для простых детей в VIII веке.
Да и вообще, Европа вошла в Средневековье равной среди первых (Китай, как минимум, а то и Индия с Персией), а вышла — не имея больше конкурентов ни в экономике, ни в технике, ни в уровне жизни, ни в науке, ни в медицине, ни в философии, ни в литературе.
>Да и вообще, Европа вошла в Средневековье равной среди первых (Китай, как минимум, а то и Индия с Персией), а вышла — не имея больше конкурентов ни в экономике, ни в технике, ни в уровне жизни, ни в науке, ни в медицине, ни в философии, ни в литературе.
Я, конечно, дилетант, но, чем больше пытаюсь разбраться именно в вопросе «как Европа из, хм, задницы мира в короткий срок превратилась в безусловного лидера на века», тем больше убеждаюсь, что ответ довольно короток: порох.
Это увязывает воедино и общественное устройство, и способы производства и способы ведения войны. Да и в приведённых Вами областях, в которых Европа «вдруг» оказалась впереди, развитие очень сильно кореллирует с развитием производства и применения пороха. Причём с отставанием, что и позволяет выяснить главный двигатель прогресса.
Ещё раз — дело далеко не просто в том, что, имея порох, можно было побеждать. Особенности производства и применения пороха увязали воедино и материальную основу и общественный строй — и дали им толчок.
А так-то да, Европа в средневековье действительно отставала от цивилизованного мира, и, можно сказать, на века отставала. Почитайте историю с подарками Васка да Гама султану, к примеру. Мозамбикского (!) султана они оскорбили своей нищетой. А ведь это уже конец 15 века.
Зато он мог бы уничтожить враз весь тамошний флот.
Кстати, даже сама эпоха великих географических открытий, сиречь океанских путешествий стала возможно именно и только благодаря пороху.
Насчёт пороха я с вами согласен, но это само по себе интересный момент: хотя порох придумали не в Европе, но именно в Европе производство пороха превратилось в разветвлённую сложную индустрию, можно даже сказать, в ВПК, когда учёные люди экспериментировали с химией, мельницы строили с расчётом на то, чтобы быстро переделывать их из зерновых или соляных в пороховые и назад, в Англию ввозили золу на поташ аж из самой России. Это ж потрясающе, если заранее не знать: не то что во Франции или Англии, а даже в России в XVI веке уже существовала профессия химинженера. И это только аспект непосредственно пороха, не считая баллистики, с которой экспериментировал и которую рассчитывал тот самый Тарталья, металлургии и проч.
> Почитайте историю с подарками Васка да Гама султану, к примеру. Мозамбикского (!) султана они оскорбили своей нищетой
Это само по себе ни о чём не говорит. Русские бояре жили богаче германских императоров, но вряд ли Германия была менее развита. Не говоря уже об индийских князьях, утопавших в роскоши, когда в нескольких шагах от их дворцов люди и в XXI веке утопают в фекалиях. Вообще привычка хамить купцам-первопроходцам из-за недостаточно щедрого подарка — очень глупый и недальновидный подход, который стоил власти, а то и жизни, не одному азиатскому/африканскому/индейскому вождю. Если б мозамбикский султан поменьше думал о бакшише и побольше о деле, глядишь, португальцы через сто лет его страну колонизировать бы не начали, и сейчас люди бы читали не историю да Гамы, а историю того безымянного султана. И ещё: тот султан, как и любой другой, был арабом. То бишь цивилизованным членом образованной, военизированной и на тот момент почти современной культуры, а богатства он получал грабежом местного чёрного населения. Причём наверняка основной статьей дохода была не какая-нибудь слоновая кость, а само население (работорговля). По крайней мере, в XVII веке именно так и было, насчёт времён да Гамы не уверен.
>производство пороха превратилось в разветвлённую сложную индустрию
Дело в том, что производство пороха при отсутствии месторождений селитры иным быть и не может. И тут совпал момент нужд пороховой индустрии и общественного устройства, которое могло это обеспечить.
Но — нужна была ещё и феодальная раздробленность. Относительно цельному государству вроде Китая порох объективно был не очень-то нужен.
А для европейских королей это была манна небесная. С одной стороны, им можно всех непослушных вассалов поубивать, с другой стороны — вассалы не могут ни производить порох (масштаба не хватает), ни хранить его (изначально порох хранился очень плохо, в том числе потому что селитра была не калиевая, а по большей части натриевая).
Заметьте — о внешних войнах ещё и речь не идёт. Порох сыграл ключевую роль в формировании европейских государств изнутри.
До того король и столицы-то толком не имел, не жил в ней, точнее. Он вынужден был непрерывно объезжать владения (с войском, ессно) и ставить на место зарвавшихся вассалов. Не зря в сказках король частенько показан в пути (след этого — и в «Обыкновенном чуде» даже).
Многие, кто не признаёт ключевую роль пороха — просто меряют современными мерками и войнами между государствами. А роль пороха во внутригосударственном «наведении порядка» была куда значительнее.
«Внешнее» применение пороха было уже следствием того, что государства окрепли и начали прибирать к рукам внешние ресурсы.
>Это ж потрясающе, если заранее не знать: не то что во Франции или Англии, а даже в России в XVI веке уже существовала профессия химинженера.
Ещё поразительнее, что всего за сотню лет пройден путь от первого знакомства с порохом (от мавров в Испании) до его вполне серьёзного применения русскими. Уж очень кстати пришёлся всем.
>Русские бояре жили богаче германских императоров, но вряд ли Германия была менее развита.
Да нет, именно так. Вся Европа была менее развита, чем Азия и даже не совсем азиатская Россия.
>Если б мозамбикский султан поменьше думал о бакшише
Если бы он знал о пороховой мощи этих корабликов и их способности к морскому плаванию — был бы и вежливее. В том-то и дело, что порох изменил и корабли. Они стали мореходными именно потому, что на них пушки поставили. Огромные, да и обычные, китайские джонки просто не выдержали бы импульса от пушечной стрельбы.
Потому с установкой пушек европейские корабли пришлось делать много прочнее. А уже потом выяснилось, что в результате даже пузатая мелочь-каравеллы способны пересечь океан.
>То бишь цивилизованным членом образованной, военизированной и на тот момент почти современной культуры, а богатства он получал грабежом местного чёрного населения. Причём наверняка основной статьей дохода была не какая-нибудь слоновая кость, а само население (работорговля). По крайней мере, в XVII веке именно так и было, насчёт времён да Гамы не уверен.
Конечно, так. Но так жили тогда все. А чего ждать можно — тяжёлой промышленности?
Видео:Решение уравнений четвертой степени. Идея метода ФеррариСкачать

Комплексные числа и их приложение к решению уравнений третьей и четвертой степени (стр. 5 )
 | Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 |
Переходить к приведенному кубическому уравнению не нужно, так как исходное уравнение само является приведенным, причем р = −6, q = 4 (1 — i).
Таким образом, получаем:

Переходя к приведенному кубическому уравнению, получаем уравнение:
причем х = у + 1 ; р = 9 ; q = −26.
Таким образом, находим:
D = (−13)2 + 33 = 196 , 
u = 
y2 = −1 + 2
y3 = −1 − 2
х1 = 3 ; х2 = 2

Ответ: а) 7 ; 1 + i

в) 3 ; 2

Видео:Формула Кардано. Решение уравнений третьей степени.Скачать

Занятие 16. Решение уравнений четвертой степени методом Феррари
Рассмотрим решение уравнений 4-й степени на конкретном примере.
Пример. Решите уравнение
Оставим в левой части уравнения члены, содержащие х4 и х3 :
Дополним левую часть полученного уравнения до полного квадрата:
х4 − х3 + 


Введем в полный квадрат левой части равенства (1) параметр r :
Откуда с учетом равенства (1) получим:

Подберем значение параметра r таким образом, чтобы дискриминант правой части равенства (2) обратился в нуль (т. е. чтобы в правой части равенства (2) также получился полный квадрат).
D =
= 
Дискриминант D равен нулю тогда и только тогда, когда число r является корнем уравнения:
В частности, D = 0 , если r = −3/2 .
Подставив значение r = −3/2 в равенство (2) , получим:




х2 − х + 2 = 0 или х2 − 5 = 0 .

Ответ: 
Задача 1. Решите уравнения:
Преобразуем уравнение (1)* по методу Феррари :
Введем в полный квадрат левой части равенства (2)* параметр r . Получим:
Используя равенство (2)*, находим :
Теперь подберем такое значение параметра r , чтобы дискриминант правой части равенства (3)* был равен нулю.

Дискриминант D равен нулю тогда и только тогда, когда число r является корнем уравнения:
В частности, D = 0 , если r = 2.
Подставив найденное значение параметра r в равенство (3)* получаем:
x2 − 2x + 3 = 0 или x2 + l = 0;

Преобразуем уравнение (4)* по методу Феррари:
Введем в полный квадрат левой части равенства (5)* параметр r . Получим:
Откуда с учетом равенства (5)* находим:
Подберем такое значение параметра r , чтобы дискриминант квадратного трехчлена в правой части равенства (6)* обратился в нуль:
− 2 r 3 + 10 r 2 − 12 r + 4 = 0 ; r 3 − 5 r 2 + 6 r − 2 = 0;
r 3 − r 2 − 4 r 2 + 4 r + 2 r − 2 = 0;
В частности, дискриминант равен нулю, если r = 1. Следовательно, подставив значение r = 1 в равенство (6)* получим:
(х2 − 3 х + 1)2 = х 2 − 4 х + 4 ; (х 2 − 3 х + 1)2 − (х − 2)2 = 0;
х 2 − 2 х − 1 = 0 или х 2 − 4 х + 3 = 0 ;
х 1, 2 = 
Ответ: a)
б) 
ИЗ ИСТОРИИ ВОЗНИКНОВЕНИЯ И РАЗВИТИЯ
ПОНЯТИЯ КОМПЛЕКСНОГО ЧИСЛА
В 1494 году в Венеции вышла книга францисканского монаха, занимавшего кафедру математики Миланского университета, Луки Пачиоли (Пачоли) (1450–1510) «Сумма (знаний) по арифметике, геометрии, отношениям и пропорциям» («Summa»), которая заканчивалась выводом: «Решение кубических уравнений вида
где а > 0 и b > 0 , столь же невозможно при современном состоянии науки, как и решение квадратуры круга циркулем и линейкой».
Однако, несмотря на это предупреждение, уже через 6 лет в 1500 году профессор Болонского университета Сципион дель Ферро (1456–1526) нашел формулу решения уравнения
где а > 0 и b > 0 . Эта формула имела вид:

Но, как это было принято в ту эпоху, дель Ферро держал свой метод в тайне.
В феврале 1535 года Николо Фонтана из Брешии (1499 (?)–1557), известный под именем Тарталья (что в переводе с итальянского означает «заика» – Фонтана сильно заикался), в ходе публичных состязаний с Фиоре (учеником дель Ферро) решил три десятка кубических уравнений вида:
где m , n , а, b − положительные числа.
В конце 30-х годов XVI века Джероламо (Джеронимо) Кардано (1501–1576) ознакомился с методом Тартальи, но поклялся его не разглашать. Однако, в 1545 году вышла книга Кардано «Великое Искусство» («Ars Magna»), в которой он приводит методы решения уравнений третьей степени (формулы дель Ферро− Тартальи) и четвертой степени (метод Людовико Феррари (1522–1565), ученика Кардано).
Как Тарталья, так и Кардано столкнулись с трудностью, которую они так и не смогли разрешить: когда величина 
Этот случай Тарталья назвал «неприводимым». Кардано, решая задачу о нахождении сторон прямоугольного участка с площадью 40 и периметром 20 , пришел к системе


Кардано назвал 
Первая догадка, как из этих «софистических чисел»
получить действительные корни, пришла замечательному ученому из Болоньи Рафаэлю Бомбелли (1530–1572), который в своем труде «Алгебра» (1572) показал, что новые числа дают при извлечении квадратного корня сопряженные числа, при сложении которых взаимно уничтожается корень квадратный из отрицательного числа.
В этой же книге Бомбелли установил четыре правила действий над новыми числами и четыре правила, связывающие «новую» (
Именно поэтому Рафаэля Бомбелли считают основоположником теории комплексных чисел.
В дальнейшем комплексные числа встречаются в работах французского математика XVII века Рене Декарта (1596–1650) при исследовании решений алгебраических уравнений второй степени. В приложении к труду «Рассуждение о Методе, чтобы направлять свой разум и отыскивать истину в науках» (1637), называемом «Геометрия» (в третьей книге − «О природе уравнений») Декарт ставит вопрос: сколько корней может иметь алгебраическое уравнение n-й степени, и дает ответ: столько же, сколько имеет единиц степень уравнения. При этом он отмечает, что надо различать «истинные» (положительные), «ложные» (отрицательные) и «воображаемые» (мнимые) корни, подчеркивая, что линии на плоскости, которые не могут пересекаться при их алгебраическом представлении в виде уравнений, дают мнимые точки пересечения.
Однако, «мнимые» величины, выдвинутые Декартом и его последователями, долго не получали признания. Даже такой выдающийся математик и философ, как , писал: «Мнимые числа − это прекрасное и чудесное убежище божественного духа, почти что амфибия бытия с небытием».
Первая удачная попытка геометрической интерпретации комплексных чисел была предпринята датским землемером и математиком Каспаром Весселем () в работе «Опыт аналитического представления направлений» (1797), которая, к сожалению, в течение столетия оставалась неизвестной.
После Весселя свою интерпретацию комплексных чисел предложил французский математик Жан Арган () в работе «Опыт некоторого представления мнимых количеств в геометрических построениях» (1806).
Однако, самую наглядную геометрическую интерпретацию комплексных чисел дал немецкий ученый, «король математиков» (1777–1855) в работе «Теория биквадратных вычетов» (1799) и позднее в «Арифметической теории комплексных чисел» (1806, 1825 и 1831), где он, рассматривая способ интерпретации новых чисел, назвал их впервые «комплексными числами» (от латинского слова «соmplex» — «объединение»), имея в виду объединение двух единиц (1 и 
(где а и b — действительные числа), оставив при этом идущее от Декарта название вторых единиц − «мнимые единицы».
В этой работе Гаусс навсегда изгнал таинственность, окружавшую мнимые числа, представив их с помощью точек плоскости. Позднее французский математик Огюстен Коши (1789–1857) в своем труде «Алгебраический анализ» (1821) продолжил эту удачную интерпретацию и ввел понятие модуля комплексного числа z = а + bi в виде неотрицательного действительного числа

1. , , Мордкович вопросы математики. 10 класс. Факультативный курс.– М.: Просвещение, 1980.
2. , , Шабунин и начала анализа. Пробный учебник 9-10 классов средней школы.– М. Просвещение, 1975.
3. Андронов действительных и комплексных чисел. – М.: Просвещение, 1975.
4. , , Пасиченко по математике. Алгебра. Справочное пособие. – М.: Наука, 1987.
5. , , Ашкенузе . Учебное пособие для 9-10 классов средней школы с математической специализацией. – М.: Просвещение, 1972.
6. , Ивашев-, Шварцбурд и математический анализ. Учебное пособие для учащихся 10 классов с углубленным изучением математики. – М.: Просвещение, 1989.
7. , , Шварцбурд изучение курса алгебры и математического анализа. – М.: Просвещение, 1991.
8. Гибш . Пособие для учителей 9−11 классов. – М.: Просвещение,1960.
9. , Солодовников – практикум по высшей алгебре для студентов−заочников физико-математических факультетов педагогических институтов. – М.: Просвещение, 1969.
10. , Новик и начала анализа. – М.: Просвещение, 1987.
11. Калнин и элементарные функции. – М.: Наука, 1964.
12. , , Яковлев и начала анализа. Часть II. Математика для техникумов. – М.: Наука, 1978.
13. Киселев . Часть II. Учебник для 8-10 классов средней школы. – М.: Учпедгиз, 1950.
14. Кочетков B. C., Кочеткова и элементарные функции. Часть II. – М.: Просвещение, 1968.
15. Крамор B. C. Алгебра и начала анализа. – М.: Высшая школа, 1981.
16. , , Яковлева по математике для поступающих в вузы. – М.: Наука, 1985.
17. Ларичев задач по алгебре. Часть II. Для 9−10 классов средней школы. – М.: Просвещение, 1965.
18. Математика в школе. № 3, 1990.
19. Математика в школе. № 6, 1992.
20. Окунев алгебра. – М.: Просвещение, 1966.
21. Петраков кружки в классах. – М.: Просвещение, 1988.
22. Петраков алгебры в педучилищах. Из опыта работы. – М.: Просвещение, 1970.
23. Понтрягин чисел. – М.: Просвещение, 1985.
24. Туманов математика. Пособие для самообразования. – М.: Просвещение, 1970.
25. , Соминский для самообразования. – М.: Наука, 1966.
26. , Пинский по методам решения задач по математике для средней школы. – М.: Наука. 1989.
27. Энциклопедический словарь юного математика. Составитель – М.: Педагогика, 1989.
28. Энциклопедия элементарной математики. Арифметика. Книга I. Под ред. – М.−Л.: Гостехиздат, 1951.
Комплексные числа и их приложение к решению
уравнений 3-й и 4-й степени
Глава 1. Комплексные числа в алгебраической
Занятие 1. Введение понятия комплексного числа.
Сложение, вычитание, умножение и
деление комплексных чисел.
Степени мнимой единицы (лекция) 6
Занятие 2. Операция сопряжения и ее свойства.
Модуль комплексного числа.
Извлечение корня квадратного
из комплексного числа (лекция) 15
Занятие 3. Действия с комплексными числами
в алгебраической форме (практика) 21 Занятие 4. Действия с комплексными числами
в алгебраической форме (практика) 27
Занятие 5. Контрольная работа №1 29
Глава 2. Геометрическая интерпретация
Занятие 6. Геометрическая интерпретация
комплексных чисел (лекция) 30
Занятия 7–8. Геометрическая интерпретация
комплексных чисел (практика) 33
Занятие 9. Контрольная работа №2 (45 мин.) 44
Глава 3. Комплексные числа в тригонометрической
Занятие 10. Тригонометрическая форма
комплексного числа, ее связь с
алгебраической формой (лекция) 45
Занятие 11. Действия с комплексными числами
в тригонометрической форме.
Возведение в натуральную степень
и извлечение корня из комплексного
числа в тригонометрической форме
(лекция) 50 Занятия 12–13. Действия с комплексными числами
в тригонометрической форме
Занятие 14. Контрольная работа №3 64
Глава 3. Решение уравнений 3-й и 4-й степени
Занятие 15. Решение уравнений третьей
степени (лекция) 65
Занятие 16. Решение уравнений третьей
степени (практика) 73
Занятие 17. Решение уравнений четвертой
степени методом Феррари (практика) 78
Из истории возникновения и развития понятия
📽️ Видео
Математика | Кубические уравнения по методу СталлонеСкачать

ФОРМУЛА КАРДАНО-ТАРТАЛЬЯ + РЕКЛАМА МФТИ!!!Скачать

Решение уравнения третьей степени x³-9x-12=0Скачать

КАК РЕШАТЬ КУБИЧЕСКИЕ УРАВНЕНИЯ | Разбираем на конкретном примереСкачать

Уравнение 4-й степени. Метод ФеррариСкачать

Формула Кардано - Тартальи// Почему выглядит именно так?Скачать

Метод неопределенных коэффициентовСкачать

Уравнение четвертой степени (Метод Феррари)Скачать

Формула Кардано для решения кубических уравненийСкачать

Кубические уравнения. Деление столбиком. Схема Горнера.Скачать

Можно ли решить уравнение 5-й степени? – математик Алексей Савватеев | НаучпопСкачать

КУБИЧЕСКИЕ УРАВНЕНИЯ 😉 #егэ #математика #профильныйегэ #shorts #огэСкачать

Как решать уравнения 4 степени Решите уравнение четвертой степени Разложить на множители Безу столбиСкачать