Формулы и уравнения по информатике (6 видео)

Содержание

Формулы и Задачи (Информатика 10)
Формулы
N = 2 i
I = K * i
Q = N L
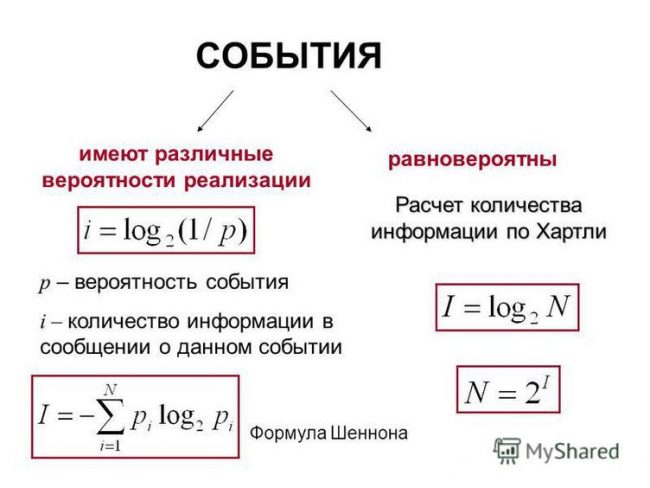
Формула Хартли:
I = log2N
Римская система счисления
Перевод чисел из других систем счисления в десятичную систему счисления
Развернутая запись целого числа:
Запись через схему Горнера:
Пример:
Развернутая запись дробного числа:
Запись через схему Горнера:
Пример:
Задачи
Алфавитный подход к измерению количества информации
Системы счисления
Логические операции
Диаграммы Венна (круги Эйлера)
Поиск номера сети
Картинки формулы по информатике (43 фото)
Формулы и уравнения по информатике
📺 Видео

Видео:Редактор формул Word, часть 1Скачать

Формулы и Задачи (Информатика 10)

Видео:Алфавитный подход к определению количества информацииСкачать

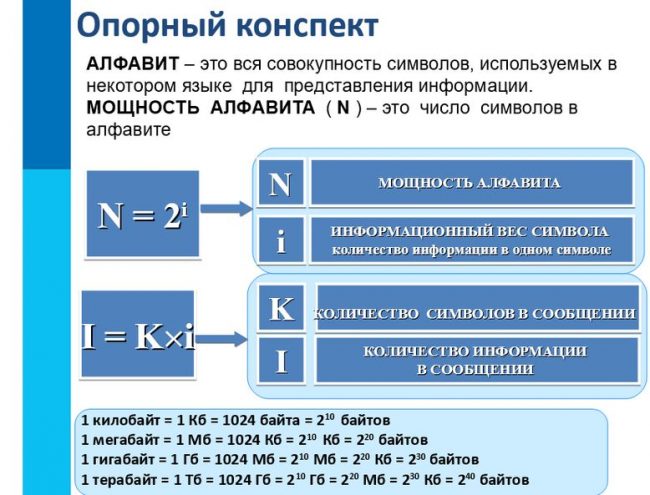
Формулы

N = 2 i

N — мощность алфавита (количество знаков в алфавите)
i — информационный вес символа алфавита (количество информации в одном символе)

**I = K * i**

I — количество информации, содержащееся в выбранном сообщении (информационный объем сообщения)
K — число символов в сообщении
i — информационный вес символа (количество информации в одном символе)

Q = N L

Q — количество разных сообщений
N — количество символов
L — длина сообщения

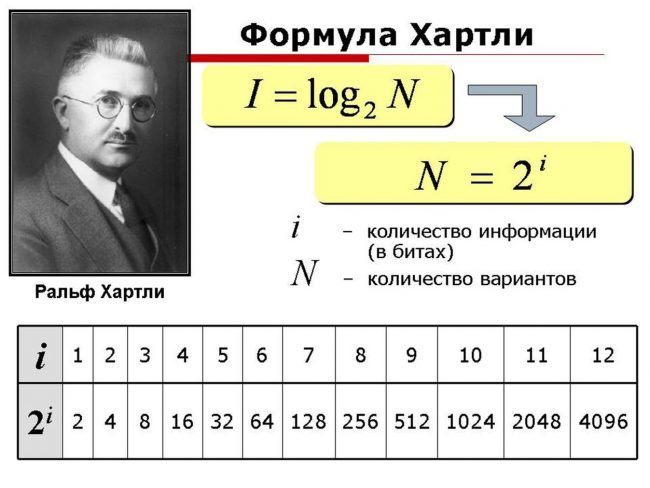
Формула Хартли:

I = log₂N

I — количество информации, содержащееся в выбранном сообщении
N — количество сообщений

Римская система счисления

I – 1 (палец),
V – 5 (раскрытая ладонь, 5 пальцев),
X – 10 (две ладони),
L – 50,
C – 100 (Centum),
D – 500 (Demimille),
M – 1000 (Mille)

Видео:Сколько решений имеет лог. уравнение (!(A *B) + C) IMP (!A * !B + D) = 1. Информатика, ЕГЭ, логикаСкачать

Перевод чисел из других систем счисления в десятичную систему счисления

Развернутая запись целого числа:

a 3a 2a 1a 0 = a 3 * p 3 + a 2 * p 2 + a 1 * p 1 + a 0 * p 0

Правило перевода числа из любой системы счисления в десятичную систему счисления — умножаем каждую цифру исходного числа на основание системы счисления в степени разряда , в котором находится эта цифра, а затем всё складываем.

Запись через схему Горнера:

p — основание системы счисления в котором представлено число.

Пример:

6 3 7 5 ₁₀ = 6 * 10 3 + 3 * 10 2 + 7 * 10 1 + 5 * 10 0
6 3 7 5 ₁₀ = (( 6 * 10 + 3 ) * 10 + 7 ) * 10 + 5
1 2 3 4 ₅ = 1 * 5 3 + 2 * 5 2 + 3 * 5 1 + 4 * 5 0 = 194₁₀
1 2 3 4 ₅ = (( 1 * 5 + 2 ) * 5 + 3 ) * 5 + 4 = 194₁₀

Развернутая запись дробного числа:

Запись через схему Горнера:

p — основание системы счисления в котором представлено число.

Пример:

0,6375 = 6 * 10 -1 + 3 * 10 -2 + 7 * 10 -3 + 5 * 10 -4
0,6375 = 10 -1 * (6 + 10 -1 * (3 + 10 -1 * (7 + 10 -1 * 5)))
0,1234 ₅ = 1 * 5 -1 + 2 * 5 -2 + 3 * 5 -3 + 4 * 5 -4
0,1234 ₅ = 5 -1 * (1 + 5 -1 * (2 + 5 -1 * (3 + 5 -1 * 4)))

Видео:Преобразование логических выражений / Упрощение выражений (практика) [Алгебра логики] #6Скачать

Задачи

Алфавитный подход к измерению количества информации

Определить количество информации в 10 страницах текста (на каждой странице 32 строки по 64 символа) при использовании алфавита из 256 символов.

информационная ёмкость символа: 256 = 2 8 =>> i = 8 бит = 1 байт
количество символов на странице:
32 * 64 = 2 5 * 2 6 = 2 11
общее количество символов:
L = 10 * 2 11
информационный объём сообщения:
I = L * i = 10 * 2 11 * 1 байт = 20 Кбайт

Системы счисления

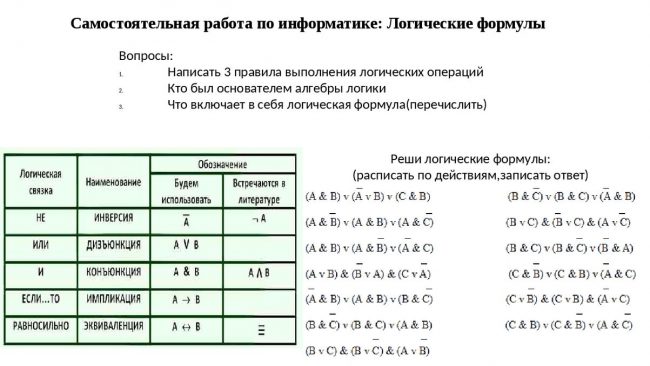
Логические операции

Логической операцией называется выбор решения (действия), исходя из заданной ситуации, определяемой набором факторов (условий).
Зависимости между логическими функциями (операциями) и логическими переменными устанавливаются с помощью таблиц истинности. Используются следующие логические операции: НЕ, И, ИЛИ, исключающее ИЛИ, тождество.

Логическая операция НЕ (инверсия, операция логического отрицания). Действие, которое определяется операцией НЕ произойдет, если отсутствует фактор его определяющий.

Таблица истинности для операции НЕ имеет вид:

A
0	1
1	0

Действие, связанное с операцией НЕ можно записать следующим образом:

Логическая операция И ( конъюнкция, операция логического умножения). Действие, которое определяется операцией И произойдет, если выполняются все влияющие на него факторы (условия).

Таблица истинности для операции И имеет вид:

A	B	X=A^B
0	0	0
0	1	0
1	0	0
1	1	1

Действие, связанное с операцией И можно записать следующим образом:

X = AB = A*B = A ^ B

Логическая операция ИЛИ ( дизъюнкция, операция логического сложения). Действие, которое определяется операцией ИЛИ произойдет, если выполняются хотя бы одно (любое), определяющее его условие.

Таблица истинности для операции ИЛИ имеет вид:

A	B	X=A v B
0	0	0
0	1	1
1	0	1
1	1	1

Действие, связанное с операцией ИЛИ можно записать следующим образом:

Логическая операция Исключающее ИЛИ. Операция Исключающее ИЛИ осуществляет суммирование по модулю два т.е. без учета переноса в старший разряд.

Таблица истинности имеет вид:

A	B	X=AB
0	0	0
0	1	1
1	0	1
1	1	0

Действие, связанное с операцией Исключающее ИЛИ можно записать следующим образом:

X = A B

Действие, связанное с операцией Импликации можно записать следующим образом:

Таблица истинности Импликации имеет вид:

A	B	A → B
0	0	1
0	1	1
1	0	0
1	1	1

Операция тождество. Операция тождество определяет тождественность аргументов.

Таблица истинности для операции тождество имеет вид:

A	B	A Ξ B
0	0	1
0	1	0
1	0	0
1	1	1

Действие, связанное с операцией тождество можно записать следующим образом:

X = A B.

Диаграммы Венна (круги Эйлера)

Поиск номера сети

Необходимо найти номер сети по IP-адресу 12.16.196.10 и маске 255.255.224.0.

Видео:Конъюнкция, дизъюнкция, импликация, эквиваленция, отрицание. На примерах из жизни. Логика.Скачать

Картинки формулы по информатике (43 фото)

Решение задач с формулами по информатике позволяет лучше понять устройство вычислительной техники. Понимание основ данной науки необходимо каждому человеку. Во многих формулах по информатике используются такие понятия как бит и байт. Они являются единицами измерения информации, которой оперирует компьютер. Предлагаем тут посмотреть красивые картинки про формулы по информатике.

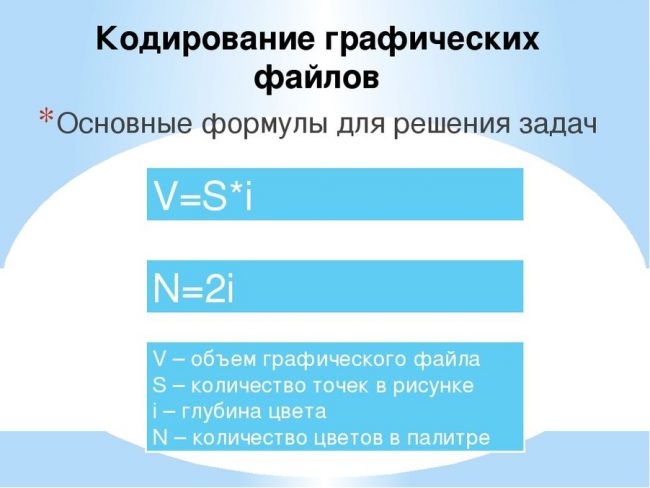
Скорость передачи файла.

Число возможных вариантов.

Прикольная формула по информатике.

Глубина кодирования в бит.

Количество символов в тексте.

Картинка формулы по информатике.

Важное уравнение информационной науки.

Формулы по информатике в опорном конспекте.

Задача на кодирование текста.

Ученый Ральф Хартли.

Замечательная формула по информатике.

Самостоятельная работа на логику.

Красивая картинка формул по информатике.

Символы в одном сообщении.

Информационный вес символа.

Познавательный материал с формулами по информатике.

Сумма элементов в задаче.

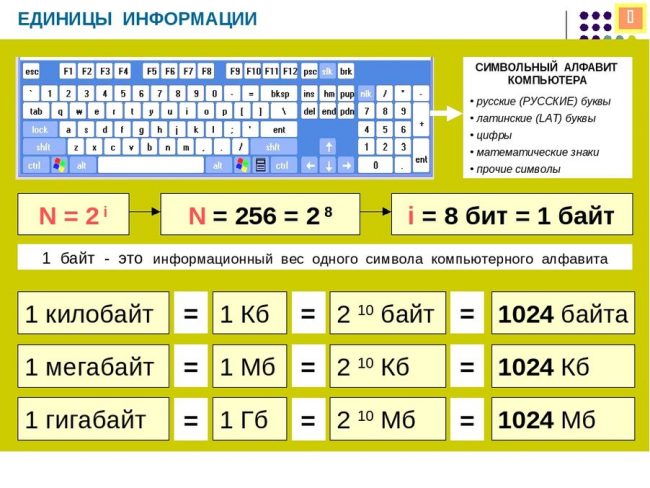
Символьный алфавит компьютера.

Сложная формула по информатике.

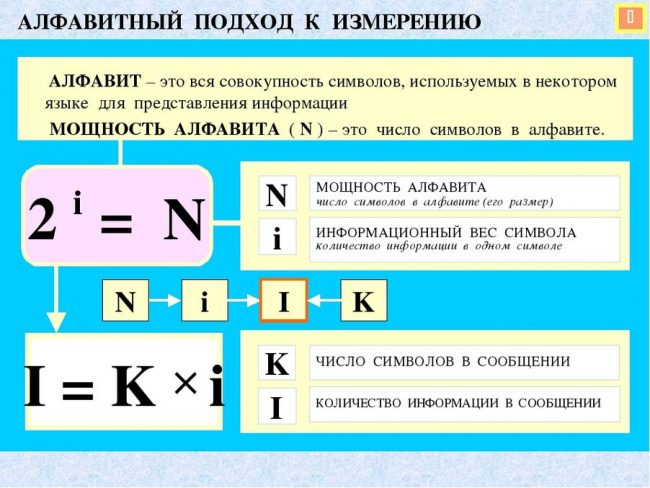
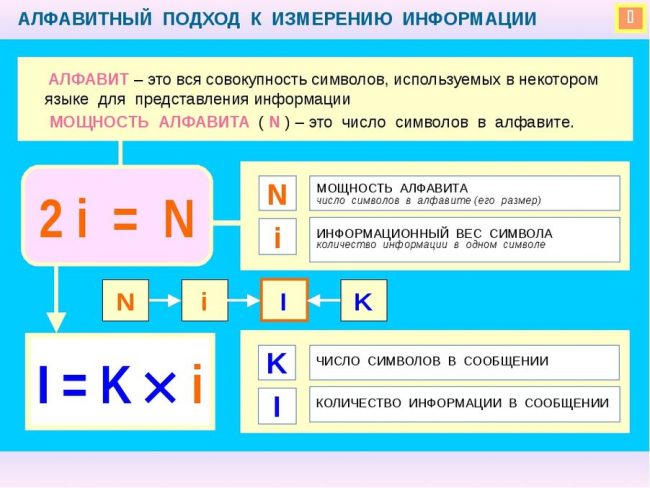
Алфавитный подход к измерению.

Небольшие подсказки для экзамена.

Формулы по информатике на картинке.

Количество информации как степень.

Символы, используемые в некотором языке.

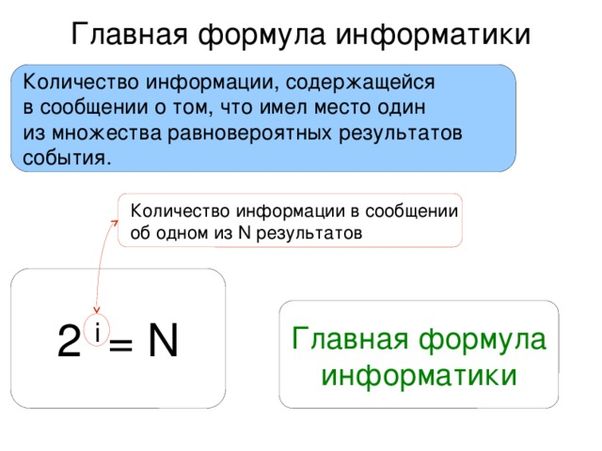
Главная формула информатики.

Простое задание с логарифмом.

Измерение информации в битах.

Красные рамки для формул по информатике.

Символы на темном фоне.

Вес символа алфавита.

Целые разряды числа в формуле по информатике.

Дано, решение, ответ.

Цветная картинка формулы по информатике.

Двоичное кодирование целых чисел.

Преобразуем логические выражения.

Разные события для формул по информатике.

Важная пометка в синей рамке.

Определения для обозначений.

Запоминаем формулу по информатике.

Количество возможных равновероятных альтернатив.

Видео:Разбор 8 задания | ОГЭ по информатике 2023Скачать

Формулы и уравнения по информатике

2) Логическое сложение или дизъюнкция:

Дизъюнкция — это сложное логическое выражение, которое истинно, если хотя бы одно из простых логических выражений истинно и ложно тогда и только тогда, когда оба простых логических выраженbя ложны.
Обозначение: F = A v B.

Таблица истинности для дизъюнкции

A	B	F
1	1	1
1	0	1
0	1	1
0	0	0

3) Логическое отрицание или инверсия:

Инверсия — это сложное логическое выражение, если исходное логическое выражение истинно, то результат отрицания будет ложным, и наоборот, если исходное логическое выражение ложно, то результат отрицания будет истинным. Другими простыми слова, данная операция означает, что к исходному логическому выражению добавляется частица НЕ или слова НЕВЕРНО, ЧТО.

Обозначение: F = ¬ A.

Таблица истинности для инверсии

A	¬ А
1	0
0	1

4) Логическое следование или импликация:

Импликация — это сложное логическое выражение, которое истинно во всех случаях, кроме как из истины следует ложь. То есть данная логическая операция связывает два простых логических выражения, из которых первое является условием (А), а второе (В) является следствием.

«A → B» истинно, если из А может следовать B.

Обозначение: F = A → B.

Таблица истинности для импликации

A	B	F
1	1	1
1	0	0
0	1	1
0	0	1

5) Логическая равнозначность или эквивалентность:

Эквивалентность — это сложное логическое выражение, которое является истинным тогда и только тогда, когда оба простых логических выражения имеют одинаковую истинность.