Видео:Гидравлический пресс. Формулы для задачСкачать
Гидравлический пресс
Видео:Гидравлические машины. 7 класс.Скачать
Определение и принцип гидравлического пресса
Гидравлический пресс — это машина, которая действует на основе законов движения и равновесия жидкостей.
Закон Паскаля лежит в основе принципа действия гидравлического пресса. Название этого устройства происходит от греческого слова гидравликос — водяной. Гидравлическим прессом называют гидравлическую машину, которая используется для прессования (сдавливания). Гидравлический пресс используют там, где необходима большая сила, например, при выдавливании масла из семян. При помощи современных гидравлических прессов можно получать силу до $^8$ньютонов.
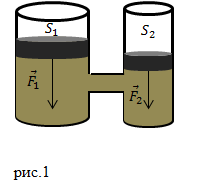
Основу гидравлической машины составляют два цилиндра разного радиуса с поршнями (рис.1), которые соединены трубой. Пространство в цилиндрах под поршнями обычно заполняют минеральным маслом.
Для того чтобы понять принцип действия гидравлической машины следует вспомнить, что такое сообщающиеся сосуды и в чем смысл закона Паскаля.
Видео:Физика 7 класс.Гидравлический пресс. Решение задачСкачать
Сообщающиеся сосуды
Сообщающимися называют сосуды, соединенные между собой и в которых жидкость может свободно перетекать из одного сосуда в другой. Форма сообщающихся сосудов может быть разной. В сообщающихся сосудах жидкость одной плотности устанавливается на одном уровне, если давления над свободными поверхностями жидкости одинаковы.
Из рис.1 мы видим, что конструктивно гидравлическая машина — это два сообщающихся сосуда разного радиуса. Высоты столбов жидкости в цилиндрах будут одинаковыми, если на поршни не действуют силы.
Видео:Физика 7 класс. §49 Гидравлический прессСкачать
Закон Паскаля
Закон Паскаля говорит нам о том, что давление, которое оказывают внешние силы на жидкость, передаются ей без изменения во все ее точки. На законе Паскаля основано действие многих гидравлических устройств: прессов, тормозных систем, гидроприводов, гидроусилителей и т.д.
Видео:ГИДРАВЛИЧЕСКИЙ ПРЕСС 7 класс Перышкин физикаСкачать
Принцип действия гидравлического пресса
Одним из самых простых и старых устройств основанных на законе Паскаля является гидравлический пресс, в котором небольшая сила $F_1$, прикладываемая к поршню небольшой площади $S_1$, преобразуется в большую силу $F_2$, которая воздействует на площадь большой площади $S_2$.
Давление, которое создает поршень номер один, равно:
Давление второго поршня на жидкость составляет:
Если поршни находятся в равновесии то давления $p_1$ и $p_2$ равны, следовательно, мы можем приравнять правые части выражений (1) и (2):
Определим, каким будет модуль силы, прикладываемой к первому поршню:
Из формулы (4), видим, что величина $F_1$ больше модуля силы $F_2$ в $frac$ раз.
И так, применяя гидравлический пресс можно небольшой силой уравновесить гораздо большую силу. Отношение $frac$ показывает выигрыш в силе.
Пресс работает так. Тело, которое необходимо спрессовать, укладывают на платформу, которая лежит на большом поршне. С помощью малого поршня создают высокое давление на жидкость. Большой поршень вместе со сжимаемым телом поднимается, упирается в неподвижную платформу, находящуюся над ними, тело сжимается.
Из малого цилиндра в большой жидкость перекачивают повторным движением поршня малой площади. Делают это следующим образом. Малый поршень поднимается, открывается клапан, при этом в пространство под малым поршнем засасывается жидкость. Когда малый поршень опускается жидкость, оказывая на клапан давление, его закрывает, при этом открывается клапан, который пропускает жидкость в большой сосуд.
Видео:Уравнение Бернулли гидравликаСкачать
Примеры задач с решением
Задание. Каким будет выигрыш в силе у гидравлического пресса, если при действии на малый поршень (площадью $S_1=10 ^2$) с силой $F_1=800$ Н, получают силу, воздействия на большой поршень ($S_2=1000 ^2$) равной $F_2=72000 $ Н?
Какой выигрыш в силе получался бы у этого пресса, если бы отсутствовали силы трения?
Решение. Выигрышем в силе называют отношение модулей полученной силы к приложенной:
Используя формулу, полученную для гидравлического пресса:
найдем выигрыш в силе при отсутствии сил трения:
Ответ. Выигрыш в силе в прессе при наличии сил трения равен $frac=90.$ Без трения он был бы равен $frac=100.$
Задание. Используя гидравлический подъемный механизм, следует поднять груз имеющий массу $m$. Какое число раз ($k$) нужно опустить малый поршень за время $t$, если за один раз он опускается на расстояние $l$? Отношение площадей поршней подъемника равно: $frac=frac$ ($n>1$). Коэффициент полезного действия машины составляет $eta $ при мощности его двигателя $N$.
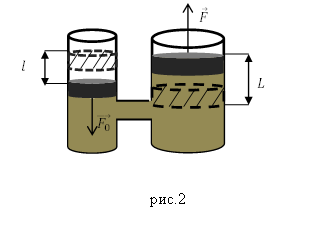
Решение. Принципиальная схема работы гидравлического подъемника изображена на рис.2., она аналогична работе гидравлического пресса.
В качестве основы для решения задачи используем выражение, связывающее мощность и работу, но при этом учтем, КПД подъемника, тогда мощность равна:
Работу производят с целью груз поднять, значит, ее найдем как изменение потенциальной энергии груза, за ноль потенциальной энергии будем считать энергию груза в месте начала его подъема ($E_$=0), имеем:
где $h$ — высота, на которую подняли груз. Приравняв правые части формул (2.1) и (2.2), найдем высоту, на которую подняли груз:
Работу, выполняемую силой $F_0$, при перемещении малого поршня найдем как:
Работа силы, которая двигает большой поршень вверх (сжимает гипотетическое тело), равна:
где $L$ — расстояние, на которое сдвигается большой поршень за один ход. Из (2.5) имеем:
Для того чтобы найти количество ходов поршней (число раз которое опустится малый поршень или поднимется большой) следует высоту поднятия груза разделить на расстояние на которое сдвигается большой поршень за один ход:
Видео:Принцип работы гидравлической машиныСкачать
Формула уравнение для гидравлического пресса
Код ОГЭ 1.21. Закон Паскаля. Гидравлический пресс.
Для жидкостей и газов справедлив закон Паскаля: Жидкости и газы передают оказываемое на них давление без изменения по всем направлениям во все точки жидкости или газа.
Закон Паскаля позволяет объяснить особое свойство сообщающихся сосудов, то есть сосудов, соединённых между собой каналом, заполненным жидкостью.
Закон сообщающихся сосудов: В сообщающихся сосудах однородная жидкость всегда устанавливается на одном уровне.
Жидкость находится в покое, поэтому на любом уровне (см. пунктир на рисунке) давление в левом сосуде должно равняться давлению в правом сосуде:
Внимание! Если в сообщающихся сосудах находятся две несмешивающиеся жидкости разными плотностями, то уровни жидкостей будут разными. Из равенства pа + p1gh1 = pа + p2gh2 следует, что отношение высот столбов жидкостей по отношению любому уровню, выше которого в каждом из сосудов находятся жидкости одного сорта, равно обратному отношению плотностей: 
Гидравлический пресс представляет собой два сообщающихся сосуда с различной площадью поперечного сечения, в которых имеются поршни, плотно прилегающие к стенкам сосудов.
Давление, оказываемое на поршень меньшей площади, в соответствии с законом Паскаля передаётся без изменения во все точки жидкости, в том числе находящиеся непосредственно под вторым поршнем:
Гидравлический пресс даёт выигрыш в силе, равный отношению площади большего поршня к площади меньшего поршня: 
Внимание! Как и в других простых механизмах, выигрыша в работе нет: при опускании малого поршня совершается работа, равная работе, совершаемой при подъёме большего поршня (если отсутствуют силы трения и сопротивления).
Конспект урока «Закон Паскаля. Гидравлический пресс».
Видео:Гидравлический пресс. Поршневой жидкостной насос | Физика 7 класс #35 | ИнфоурокСкачать
Гидравлический пресс
Видео:Опыты по физике. Устройство и действие гидравлического прессаСкачать
Содержание
Чтобы рассмотреть устройство гидравлического пресса, сначала дадим определение гидравлической машины:
Гидравлическая машина (от греческого «гидравликос» — водяной) – это машина, действие которой основано на законах движения и равновесия жидкостей и объясняется законом Паскаля.
Гидравлическая машина в основе представляет собой два цилиндра разного диаметра, в каждом из которых имеется поршень (рисунок 4). Цилиндры соединены между собой трубкой и заполнены жидкостью (водой, маслом или др.).
Так как эти цилиндры представляют собой сообщающиеся сосуды, высота столба жидкости в них будет одинакова, пока на поршни находятся в состоянии покоя.
Рисунок 4. Схематическое изображение принципа работы гидравлической машины.
Теперь рассмотрим ситуацию, когда на поршни действуют некоторые силы $F_1$ и $F_2$, а $S_1$ и $S_2$ — площади поршней. По определению давления мы уже знаем, что $p=frac$, тогда:
Давление, оказываемое меньшим поршнем: $p_1=frac$
Давление, оказываемое большим поршнем: $p_2=frac$
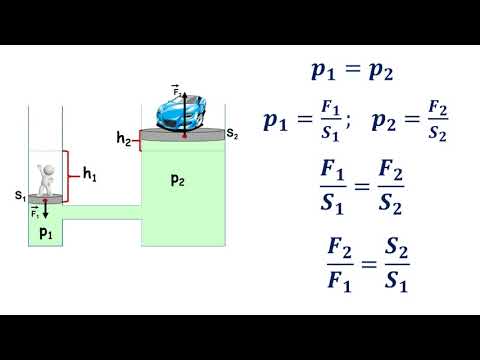
Так как сосуды соединены между собой, по закону Паскаля $p_1 = p_2$ или $frac = frac$, откуда следует, что
Сила, действующая на поршень, прямо пропорциональна площади этого поршня. Следовательно, сила $F_2$ больше силы $F_1$ во столько раз, во сколько раз площадь большего поршня $S_2$ больше площади меньшего $S_1$.
Например, если площадь большого поршня $300 см^2$, а маленького $3 см^2$ и на него действует сила $100 Н$, то на большой поршень будет действовать сила $10 000 Н$.
Показательное отношение $frac$ называют выигрышем в силе. Другими словами, с помощью гидравлической машины можно малой силой уравновесить большую силу.
Гидравлический пресс – это гидравлическая машина, служащая для сдавливания (прессования).
Гидравлические прессы эффективно работают для преобразования малой силы в большую: используются для спрессовывания семян при изготовлении масла, для склеивания строительных материалов, для штамповки ювелирных изделий. Современные гидравлические прессы могут развивать силу в сотни миллионов ньютонов (рисунок 5).
Рассмотрим устройство гидравлического пресса:
Усложняем схему устройства гидравлической машины: теперь над большим поршнем 2 имеется платформа, куда мы помещаем прессуемое тело 1.
С помощью малого поршня 3 мы создаем большое давление на жидкость, которое также начинает действовать на поршень 2. Происходит это потому, что давление передается без изменения в каждую точку жидкости (закон Паскаля).
Площадь поршня 2 больше площади поршня 3, поэтому и сила, действующая на него, будет больше (давление одинаковое). Под действием этой силы поршень 2 начинает подниматься и придавливает прессуемое тело к неподвижной верхней платформе.
Здесь же установлен манометр 4 для контроля давления жидкости и предохранительный клапан 5 (автоматически открывается, когда давление превышает максимально допустимое в данном устройстве значение).
При повторяющихся движениях поршня 3 жидкость снова попадает из малого цилиндра в большой: малый поршень поднимается и открывается клапан 6. Пространство под поршнем моментально заполняется жидкостью. Когда же малый поршень 3 опускается, клапан 6 закрывается под давлением жидкости, а клапан 7 открывается. Так жидкость снова оказывается в большом сосуде.
Видео:Урок 60 (осн). Гидравлический прессСкачать
Другие устройства и задачи
Еще одной известной разновидностью гидравлических машин является гидравлический тормоз. На данный момент практически все автомобили оснащены гидравлическими тормозами. Рассмотрим принцип работы, используя упрощенную схему (рисунок 7).
Водитель ногой создает давление на педаль тормоза, это действие передается на поршень цилиндра с тормозной жидкостью. По закону Паскаля это давление передается одинаково во все тормозные цилиндры колес автомобиля. Под давлением жидкости подвижные поршни, находящиеся в тормозном устройстве, расходятся и прижимают тормозные колодки к тормозным барабанам – вращение колес прекращается.
Другое распространенное устройство – гидравлический домкрат (рисунок 8). Принцип действия домкрата идентичен принципу действия гидравлического пресса, но с помощью него можно поднимать очень тяжелые предметы.
Жидкостью здесь выступает гидравлическое масло, а также имеется нагнетательный и спускной клапана.
📺 Видео
Закон БернуллиСкачать
Урок 61 (осн). Задачи на гидравлический пресс - 1Скачать
Физика 10 класс : Гидравлический прессСкачать
Физика 7 класс Гидравлический прессСкачать
Урок 132. Основные понятия гидродинамики. Уравнение непрерывностиСкачать
Опыты по физике. Модель гидравлического прессаСкачать
7 класс. Гидравлические машины.Скачать
Гидравлическая машинаСкачать
Урок гидравлики - 01 - Основные положенияСкачать
Гидравлический прессСкачать
