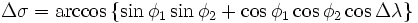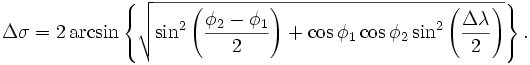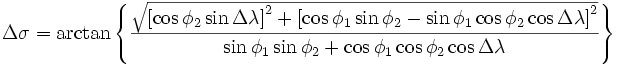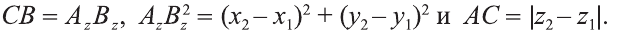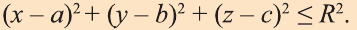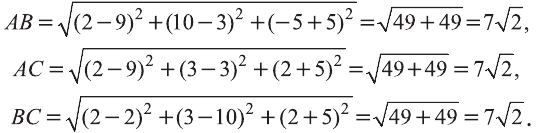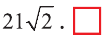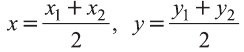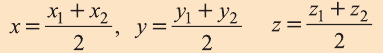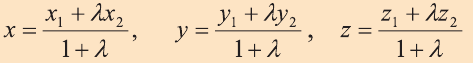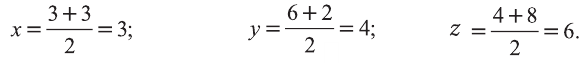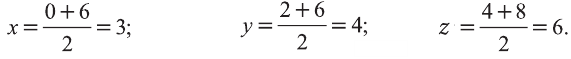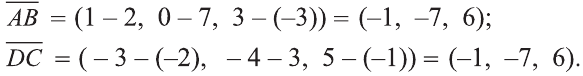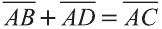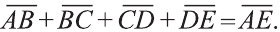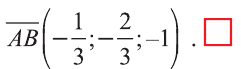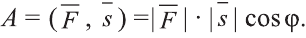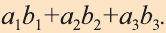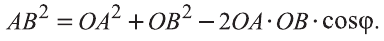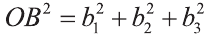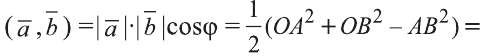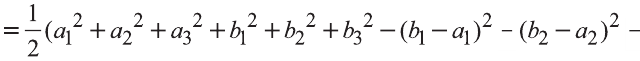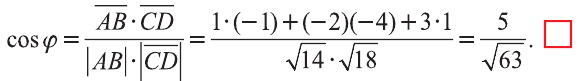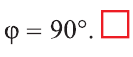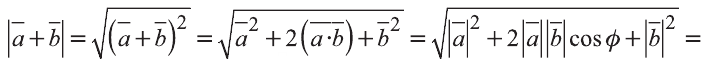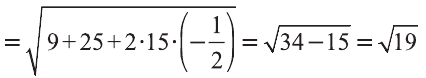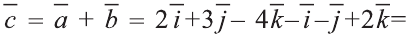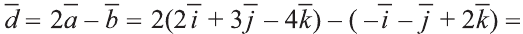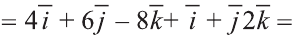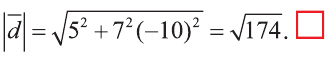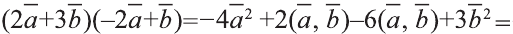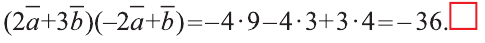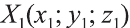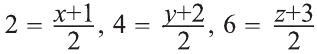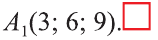Формула расстояния между двумя точками в пространстве уравнения сферы

Видеоурок: Формула расстояния между двумя точками

Лекция: Формула расстояния между двумя точками; уравнение сферы

Расстояние между двумя точками

Для нахождения расстояния между двумя точками на прямой в предыдущем вопросе мы использовали формулу d = х₂ – х_1.

Но, что касается плоскости, дела обстоят иначе. Не достаточно просто найти разность координат. Для нахождения расстояния между точками по их координатам следует воспользоваться следующей формулой:

Например, если у Вас имеются две точки с некоторыми координатами, то найти расстояние между ними можно следующим образом:

АВ = ((4 + 4) 2 + (-1 – 6) 2 ) 1/2 ≈ 10,6.

То есть для вычисления расстояния между двумя точками на плоскости необходимо найти корень из суммы квадратов разностей координат.

Если необходимо найти расстояние между двумя точками на плоскости, следует воспользоваться аналогичной формулой с дополнительной координатой:

Уравнение сферы

Для задания сферы в пространстве следует знать координаты её центра, а также её радиус, чтобы воспользоваться следующей формулой:

Данное уравнение соответствует сфере, центр которой находится в начале координат.

Если же центр сферы сдвинут на некоторое количество единиц по осям, то следует воспользоваться следующей формулой:

Видео:Расстояние между двумя точками. Координаты середины отрезка.Скачать

GIS-LAB

Географические информационные системы и дистанционное зондирование

Видео:11 класс, 20 урок, Уравнение сферыСкачать

Вычисление расстояния и начального азимута между двумя точками на сфере

Измерение расстояния и начального азимута между точками без проекционных преобразований

Видео:Длина отрезкаСкачать

Содержание

Видео:Расстояние между точкамиСкачать

[править] Введение

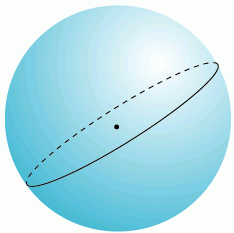
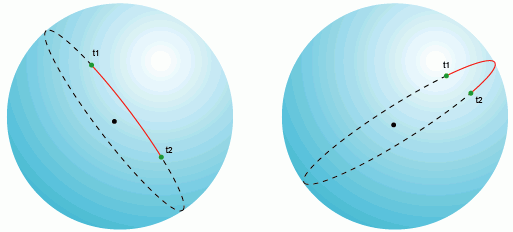
Длина дуги большого круга – кратчайшее расстояние между любыми двумя точками находящимися на поверхности сферы, измеренное вдоль линии соединяющей эти две точки (такая линия носит название ортодромии) и проходящей по поверхности сферы или другой поверхности вращения. Сферическая геометрия отличается от обычной Эвклидовой и уравнения расстояния также принимают другую форму. В Эвклидовой геометрии, кратчайшее расстояние между двумя точками – прямая линия. На сфере, прямых линий не бывает. Эти линии на сфере являются частью больших кругов – окружностей, центры которых совпадают с центром сферы.

Начальный азимут — азимут, взяв который при начале движения из точки А, следуя по большому кругу на кратчайшее расстояние до точки B, конечной точкой будет точка B. При движении из точки A в точку B по линии большого круга азимут из текущего положения на конечную точку B постоянно меняется. Начальный азимут [angles-rhumb.html отличен от постоянного], следуя которому, азимут из текущей точки на конечную не меняется, но маршрут следования не является кратчайшим расстоянием между двумя точками.

Через любые две точки на поверхности сферы, если они не прямо противоположны друг другу (то есть не являются антиподами), можно провести уникальный большой круг. Две точки, разделяют большой круг на две дуги. Длина короткой дуги – кратчайшее расстояние между двумя точками. Между двумя точками-антиподами можно провести бесконечное количество больших кругов, но расстояние между ними будет одинаково на любом круге и равно половине окружности круга, или pi*R, где R – радиус сферы.

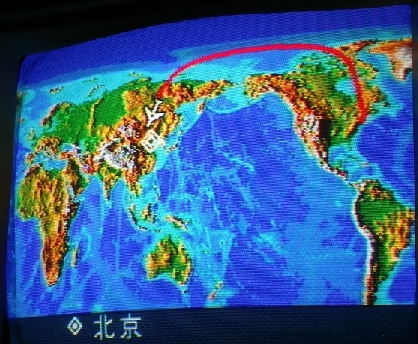
На плоскости (в прямоугольной системе координат), большие круги и их фрагменты, как было упомянуто выше, представляют собой дуги во всех проекциях, кроме гномонической, где большие круги — прямые линии. На практике это означает, что самолеты и другой авиатранспорт всегда использует маршрут минимального расстояния между точками для экономии топлива, то есть полет осуществляется по расстоянию большого круга, на плоскости это выглядит как дуга.

Форма Земли может быть описана как сфера, поэтому уравнения для вычисления расстояний на большом круге важны для вычисления кратчайшего расстояния между точками на поверхности Земли и часто используются в навигации.

Вычисление расстояния этим методом более эффективно и во многих случаях более точно, чем вычисление его для спроектированных координат (в прямоугольных системах координат), поскольку, во-первых, для этого не надо переводить географические координаты в прямоугольную систему координат (осуществлять проекционные преобразования) и, во-вторых, многие проекции, если неправильно выбраны, могу привести к значительным искажениям длин в силу особенностей проекционных искажений.

Известно, что более точно описывает форму Земли не сфера, а эллипсоид, однако в данной статье рассматривается вычисление расстояний именно на сфере, для вычислений используется сфера радиусом 6372795 метров, что может привести к ошибке вычисления расстояний порядка 0.5%.

Видео:18. Расстояние от точки до прямой в пространствеСкачать

[править] Формулы

Существует три способа расчета сферического расстояния большого круга (подробнее).

[править] Сферическая теорема косинусов

В случае маленьких расстояний и небольшой разрядности вычисления (количество знаков после запятой), использование формулы может приводить к значительным ошибкам связанным с округлением. Графическое изображение формул здесь и далее — из Википедии.

— широта и долгота двух точек в радианах

— разница координат по долготе

— угловая разница

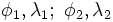
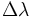
Для перевода углового расстояния в метрическое, нужно угловую разницу умножить на радиус Земли (6372795 метров), единицы конечного расстояния будут равны единицам, в которых выражен радиус (в данном случае — метры).

[править] Формула гаверсинусов

Используется, чтобы избежать проблем с небольшими расстояниями.

[править] Модификация для антиподов

Предыдущая формула также подвержена проблеме точек-антиподов, чтобы ее решить используется следующая ее модификация.

[править] Реализация на Avenue

На языке Avenue, используя последнюю формулу для вычисления расстояния большого круга между двумя точками, можно использовать следующий код. Точки для вычисления передаются другим скриптом, либо добавляются в начало данного в виде pnt = point.make(long, lat) (скачать скрипт):

Для вызова процедуры расчета длин приведенной выше, можно также воспользоваться следующим скриптом, результатом его работы будет расчет длин между точкой testpont до всех точек активной темы вида и запись результата в поле Newdist атрибутивной таблицы этой темы:

[править] Реализация на языке Python

Реализует полный вариант расчета через atan2(), более универсальнее, чем вариант для Avenue. (скачать скрипт)

[править] Реализация в Excel

Скачать пример расчета расстояния большого круга и начального азимута в Excel. Демонстрирует расчеты через закон косинусов, гаверсинус, полное уравнение и полное уравнение через atan2().

Можно также воспользоваться следующей функцией:

[править] Проверочный набор данных

Если все считается правильно, должны быть получены следующие результаты (координаты точек даны как широта/долгота, расстояние в метрах, начальный угол в десятичных градусах):

Видео:Уравнение окружности и формула расстояния между точками на плоскостиСкачать

[править] Ссылки по теме

Последнее обновление: 2014-05-14 23:41

Дата создания: 06.06.2006
Автор(ы): Максим Дубинин

Видео:Расстояние между двумя точками (прямоугольная система координат на плоскости).Скачать

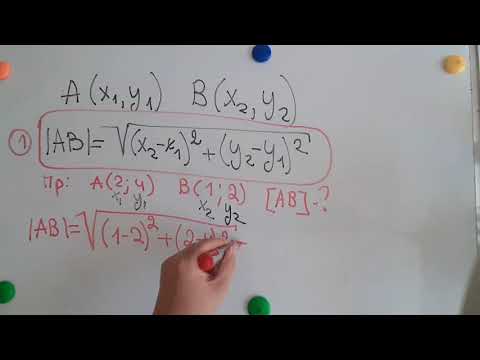
Система координат в пространстве — определение с примерами решения

Содержание:

Видео:Математика без Ху!ни. Уравнение плоскости.Скачать

Система координат в пространстве

Декартова система координат в пространстве

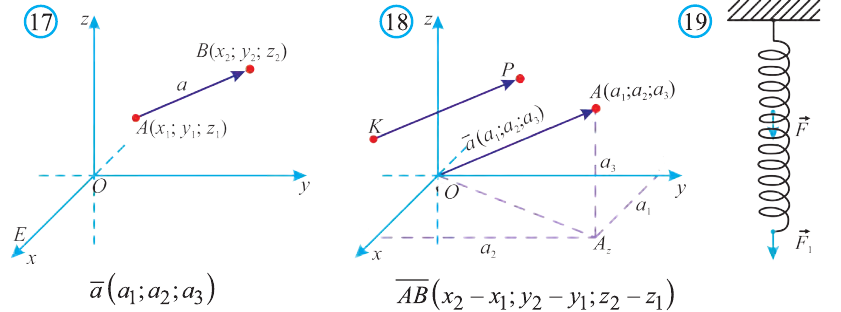
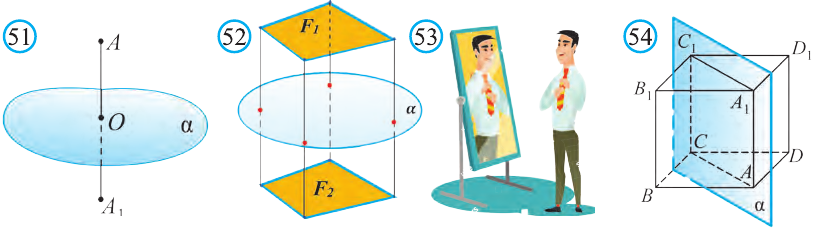
Вы познакомились с декартовой системой координат на плоскости в предыдущих классах. Систему координат в пространстве введём аналогично тому, как это было сделано на плоскости. Рассмотрим три взаимно перпендикулярных оси Ох, Оу и Оz, пересекающихся в точке О, являющейся началом координат. Через каждую пару этих прямых проведём плоскости Оху, 0xz и Оуz (рис. 1). Таким образом вводится система координат в пространстве, при этом

точку О — называют началом координат, прямые Ох, Оу и Оz — осями координат, Ох — ось абсцисс, Оу — ось ординат и Оz — ось аппликат, плоскости Оху, Оуz и Охz — координатными плоскостями.

Координатные плоскости делят пространство на 8 октант (получетвертей) (рис. 1).

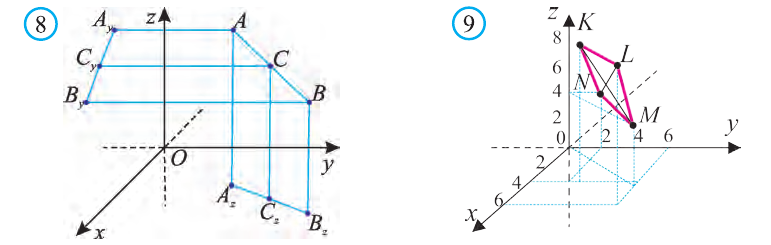
Пусть в пространстве задана произвольная точка А. Через эту точку проведём плоскости, перпендикулярные плоскостям Охz, Оуz и Охz (рис. 2). Одна из этих плоскостей пересечёт ось Ох в точке Ах.

Координату Ах на оси Ох называют координатой х или абсциссой точки А.

Аналогично определяют у — координату (ординату) и z- координату (аппликату) точки А.

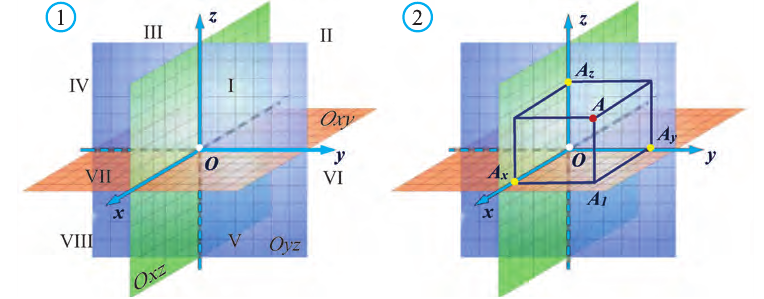
Координаты точки А записывают в виде А (х; у; z) или короче (х; у; z). Точки, изображённые на рисунке 3, имеют следующие координаты: А (0; 5; 0), B (4; 0; 0), М (0; 5; 4), К (2; 3; 4), Р (-2; 3; -4).

Пример:

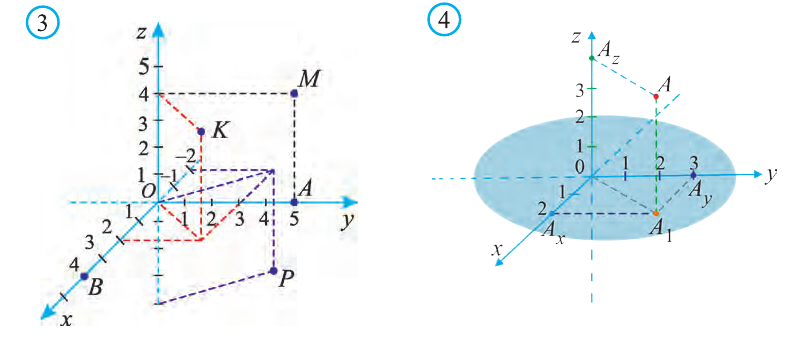
Пусть в пространстве в декартовой системе координат

задана точка А (2; 3; 4). Где она расположена?

Решение:

От начала координат в положительном направлении осей Ох и Оу отложим отрезки ОА_х = 2 и ОА_у = 3 (рис. 4).

Через точку А_х проведём прямую, лежащую в плоскости Оху и параллельную оси Оу. А через точку Аy проведём прямую, лежащую в плоскости Оху и параллельную оси Ох. Точку пересечения этих прямых обозначим A₁ . Через точку A₁ проведём прямую, перпендикулярную плоскости Оху и на ней в положительном направлении Oz отложим отрезок АА₁ = 4. Тогда точка А (2; 3; 4) и будет искомой точкой.

Пользуясь системой координат, созданной для современных программируемых станков и автоматизированных роботов, составляются программы, на основе которых обрабатываются металлы (рис. 5).

Расстояние между двумя точками

1.Сначала рассмотрим случай, когда прямая АВ не параллельна оси Оz (рис. 6). Через точки А и В проведём прямые, параллельные оси Оz. И пусть они пересекают плоскость Оху в точках А_z и В_z .

Координаты х и у этих точек соответственно равны координатам х и у точек А, В, а координаты z равны 0.

Теперь через точку В проведём плоскость а, параллельную плоскости Оху. Она пересечёт прямую АА_z в некоторой точке С.

По теореме Пифагора: АВ 2 = АС 2 + СВ 2 .

Однако

Поэтому

2.Пусть отрезок АВ параллелен оси Оz, тогда 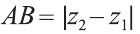и, так как

Следовательно, расстояние между двумя точками А и В:

(1)

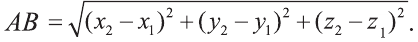
Примечание. Формула (1) выражает длину диагонали прямоугольного параллелепипеда, измерения которого равны

Уравнение сферы и шара

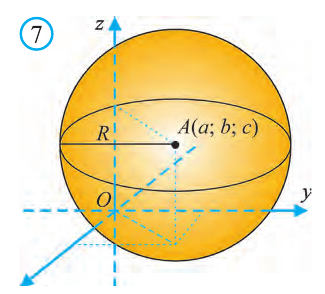
Известно, что множество всех точек М (х; у; z), расположенных на расстоянии R от данной точки А (а; Ь; с) образуют сферу (рис. 7). Тогда по формуле (1) координаты всех точек, расположенных на сфере радиуса R с центром в точке А (а; b; с), удовлетворяют равенству

Отсюда, ясно, что неравенство для точек шара радиуса R с центром в

точке А (а; b; с) имеет вид:

Пример:

Найдите периметр треугольника ABC с вершинами в

Решение:

Р=АВ+АС+ВС периметр треугольника ABC. Воспользовавшись формулой 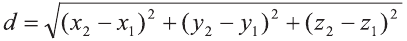расстояния между двумя точками, найдём длины сторон треугольника:

Следовательно, треугольник ABC равносторонний и его периметр .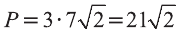

Ответ:

Координаты середины отрезка

Пусть А (x₁; y₁;z₁) и В (х₂; у₂; z₂) — произвольные точки, точка С (х; у; z) середина отрезка AB (рис. 8).

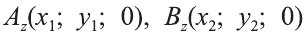
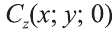
Через точки А, В и С проведём прямые, параллельные оси пересекающие плоскость Оху в точках и . Тогда по теореме Фалеса точка С_z — середина отрезка А_zВ_z.

Отсюда по формулам нахождения координат середины отрезка на плоскости

Чтобы найти координату z, нужно вместо плоскости Оху рассмотреть плоскость 0xz или Оуz.

Тогда и для z получим формулу, подобную вышеприведённой.

Аналогично, используя координаты концов A и B отрезка AB, по формулам

находят координаты точки Р(х1;у]; г,), делящей отрезок АВ в отношении X САР: РВ = X).

Доказательство: Для решения задачи используем признак параллелограмма: Четырёхугольник, точка пересечения диагоналей которого делит их пополам, является параллелограммом.

Координаты середины отрезка МК:

Координаты середины отрезка NL:

Координаты середин отрезков МК и NL равны. Это говорит о том, что отрезки пeрeсeкаются и в точке пeрeсeчeния делятся пополам. Следовательно, четырёхугольник MNLK — параллелограмм.

В переписке с известным целителем и математиком Абу Али ибн Сино Абу Райхон Беруни задаёт следующий вопрос: «Почему Аристотель и другие (философы) называют шесть сторон?»

Рассматривая шестисторонний куб, Беруни говорит о фигурах «с другим количеством сторон» и добавляет, что «шарообразные фигуры не имеют сторон.» А Ибн Сино отвечает, что «во всех случаях нужно считать, что сторон шесть, так как у каждой фигуры, независимо от её формы, есть три измерения — длина, глубина и ширина».

Здесь Ибн Сино имеет ввиду три координаты, именуемые условно «шесть сторон».

В произведении «Канон Масъуда» Беруни приводит точное математическое определение шести сторон: «Сторон шесть, так как они ограничивают движение фигур по своим измерениям. Измерений три: длина, ширина и глубина. А их в два раза больше самих измерений.»

В предыдущих книгах автор определяет положение небесных тел с помощью двух координат относительно небесной сферы — эклиптического уравнения. Либо через те же координаты, но относительно небесного экватора или горизонта. Однако при определении взаимного расположения звёзд и небесных светил придётся учитывать и случаи затмений. Вот в таких случаях появляется необходимость в третьей сферической координате. Эта необходимость привела Беруни к отказу от теории небесных координат.

Векторы в пространстве и действия над ними

Векторы в пространстве

Понятие вектора в пространстве вводят также как на плоскости.

Вектором в пространстве называют направленный отрезок. Основные понятия, относящиеся к векторам в пространстве, аналогичны этим понятиям на плоскости: длина (модуль), направление вектора, равенство векторов.

Координатами вектора с началом в точке А (х₁; у₁; z₁) и концом в точке В (х₁; у₁; z₁) называют числа 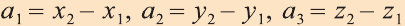, (рис. 17).

Приведем без доказательства свойства векторов, аналогичных свойствам на плоскости.

Также как на плоскости, соответствующие координаты равных векторов равны и, обратно, векторы с равными координатами равны.

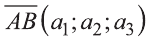
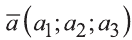
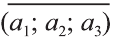
Hа основании этого вектор можно обозначить как или или кратко (рис. 18).

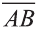
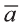
Вектор можно записать и без координат (или ). В этой записи

на первом месте начало вектора, а на втором — конец.

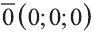
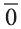
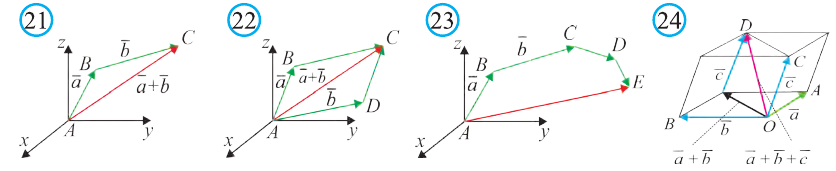
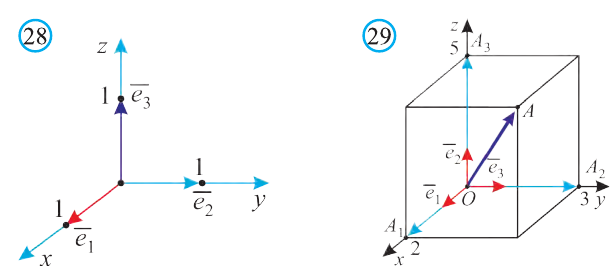
Вектор с координатами, равными нулю, называют нулевым вектором и обозначают или , направление этого вектора не определено.

Если начало вектора расположено в начале координат О, а числа а₁,

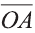
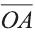
координатами вектора : (а₁; а₂; а₃).

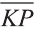
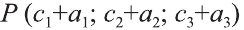
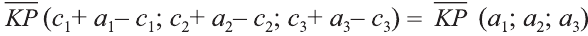
Однако вектор в пространстве с началом в точке К(с₁; с₂; с₃) и концом в точке будет иметь те же координаты: .

Отсюда следует, что вектор можно приложить к любой точке пространства. В геометрии мы рассматриваем такие свободные векторы. Но в физике, обычно вектор связан с некоторой точкой. Например, воздействие силы приложенная к пружине F на рисунке 19 зависит от точки её приложения.

Длинной вектора называют длину направленного отрезка

изображающего его (рис. 17). Длину вектора 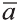записывают

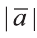
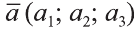
так. Длина вектора , заданного координатами,

вычисляется по формуле .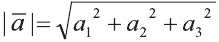

Пример:

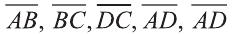
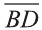
Даны точки А (2; 7;-3),В (1; 0; 3), С (-3;-4; 5) и D (-2; 3; -1). Какие из векторов и равны между собой?

Решение:

У равных векторов равны соответствующие координаты. Поэтому найдём координаты векторов:

Следовательно, .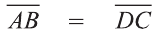

Докажите самостоятельно, что

Действия над векторами в пространстве

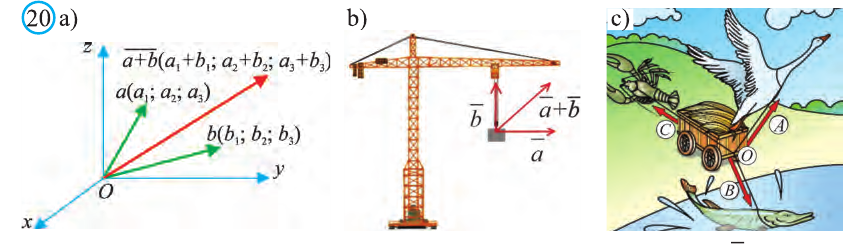
Действия над векторами. Сложение векторов, умножение на число и их скалярное произведение определяется также как на плоскости.

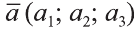
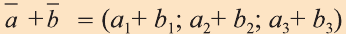
Суммой векторов и (b₁; b₂; b₃); называют вектор (рис. 20).

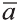
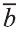
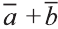
Пусть кран на рисунке 20.b движется вдоль вектора , а груз относительно крана вдоль вектора . В результате груз движется вдоль вектора . Поэтому из рисунка 20.с, на котором изображён сюжeт басни русского писателя И.А.Крылова, ясно, что герои басни не смогут сдвинуть телегу с места.

Свойства суммы векторов

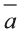
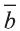
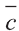
Для любых векторов , и имеют место следующие свойства:

a) — переместительный закон сложения векторов;

b) — распределительный закон сложения.

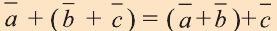
Правило треугольника сложения векторов

Для любых точек А, В и С (рис. 21):

Правило параллелограмма сложения векторов

Если АВСD — параллелограмм (рис. 22), то

Правило многоугольника сложения векторов

Если точки А, В, С, D и Е — вершины многоугольника (рис. 23), то

Правило параллелепипеда сложения трёх векторов, не лежащих в одной плоскости. Если АВСDА₁В₁С₁D₁ параллелепипед (рис. 24), то

.

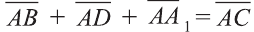
Вектор ​​​​​​= (a1; a₂; a₃) — называют умножением вектора

(a₁; a₂; a₃) на число (рис. 25). Свойства операции умножения вектора на число.

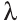
Для любых векторов и и чисел и

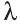
а);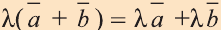

b);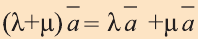

c) 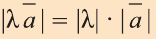и направление вектора

совпадает с направлением вектора , если ,

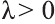
противоположно направлению вектора , если .

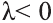
Коллинеарные и компланарные векторы

Пусть заданы ненулевые векторы и . Если векторы

и сонаправлены или противоположно направлены,

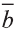
то их называют коллинеарными векторами (рис. 26).

Свойство 1. Если для векторов и имеет место равенство , то они коллинеарны и наоборот.

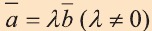
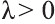
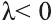
Если , то векторы и сонаправлены , если, то

противоположно направлены .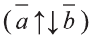

Свойство 2. Если векторы (a₁; a₂; a₃) и (b₁; b₂; b₃) коллинеарны,

то их соответствующие координаты пропорциональны:

и наоборот.

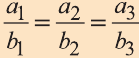
Пример:

Найдите вектор с началом в точке А (1; 1; 1) и концом в точке В, лежащей в плоскости Оху, коллинеарный вектору ( 1; 2; 3).

Решение:

Пусть точка В имеет координаты В (х; у; z). Так как точка В лежит в плоскости Оху, то z=0. Тогда 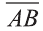(х — 1 ;у — 1; — 1).

По условию задачи векторы 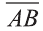(х — 1 ;у — 1; — 1) и (1, 2, 3) коллинеарны. Следовательно, их координаты пропорциональны.

Тогда получаем следующие пропорции .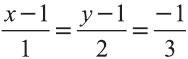

Откуда находим , .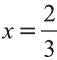

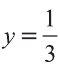
Итак,

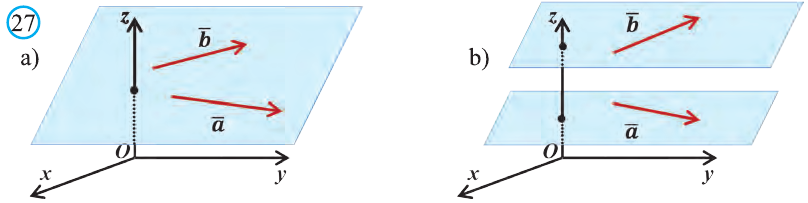
Векторы, лежащие в одной плоскости или параллельных плоскостях, называют компланарными векторами (рис. 27).

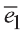
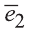
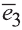
Векторы (1; 0; 0), (0; 1; 0) и (0; 0; 1) называют ортами (рис. 28).

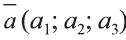
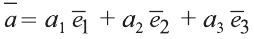
Любой вектор можно единственным образом разложить по ортам, то есть представить в виде (рис. 29).

Точно также, если заданы три нeкомпланарных вектора и , то любой вектор можно единственным образом представить в виде:

.

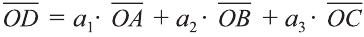
Здесь 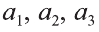некоторые действительные числа. Тогда говорят, что вектор разложен по заданным векторам.

Скалярное произведение векторов

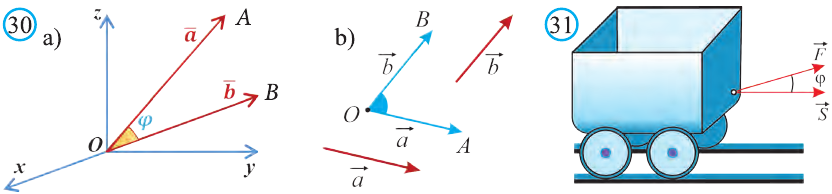
Углом между ненулевыми векторами и называют угол между направленными отрезками векторов = и =, исходящих из точки О (рис. 30).

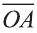
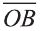
Угол между векторами и обозначают так .

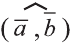
Скалярным произведением векторов и называют произведение длин этих векторов на косинус угла между ними.

Если один из векторов нулевой, то скалярное произведение этих векторов равно нулю.

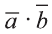
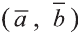
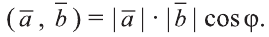
Скалярное произведение обозначают или . По определению (1)

Из определения следует, что если скалярное произведение векторов и равно нулю, то эти векторы перпендикулярны и наоборот.

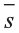
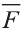
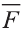
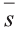
В физике работа A, выполненная при движении тела на расстоянии , под воздействием силы (рис. 31), равна скалярному произведению силы на расстояние:

Свойство. Если 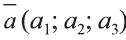и (b₁; b₂; b₃), то () =

Доказательство. Приложим векторы 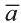и к началу

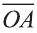
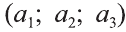
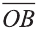
координат О (рис.32). Тогда = и = (b₁; b₂; b₃).

Если векторы неколлинеарны, то получаем треугольник АВО , для которого справедлива теорема косинусов.

Тогда .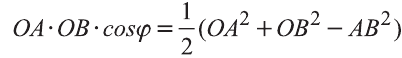

Однако, ,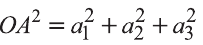

и .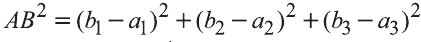

Следовательно,

.

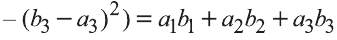
Самостоятельно докажите, что и в случае, когда данные векторы коллинеарны , также выполняется

это равенство.

Свойства скалярного произведения векторов

1. — переместительное свойство.

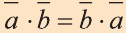
2. — распределительное свойство.

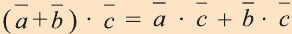
3. — сочетательное свойство.

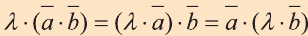
4.Если векторы а и b являются сонаправленными коллинеарными

векторами, то 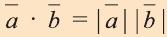, так как соs 0° = 1.

5.Если же векторы противоположно направлены, то 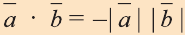, так как cos l80° = -1.

6. .

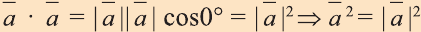
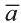
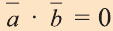
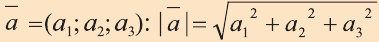
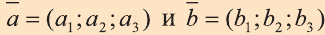
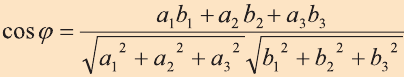
7. Если вектор перпендикулярен вектору , то . Следствия: а) Длина вектора ; (1) b) косинус угла между векторами

: ; (2)

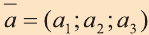
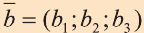
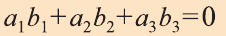
с) условие перпендикулярности векторов и

.

(3)

Пример:

— заданные точки. Найдите косинус угла между векторами .

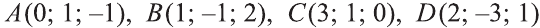
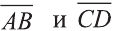
Решение:

Найдём длины векторов :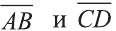

,

.

,

.

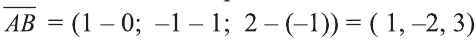
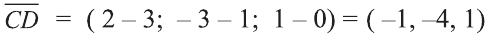
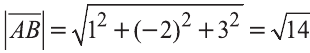
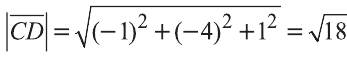
Пример:

Найдите угол между векторами .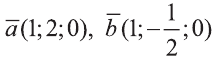

Решение:

Итак,

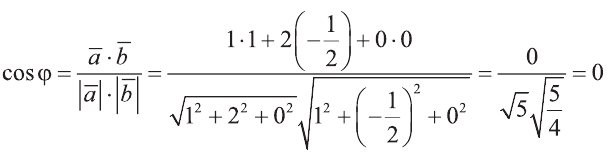
Пример:

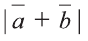
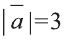
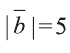
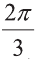
Найдите , если , и угол между векторамии равен .

Решение:

Пример:

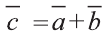
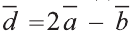
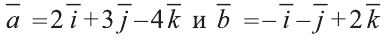
Найдите координаты и длины векторов 1); 2), если .

Решение:

Подставим в выражения искомых векторов разложения векторов и по координатам:

1)

. Следовательно,.

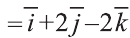
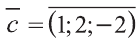
Тогда.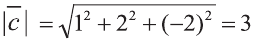

2)

.

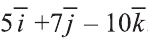
Следовательно, .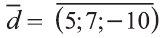

Тогда

Пример:

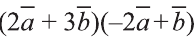
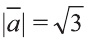
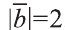
Найдите произведение, если угол между векторами и равен 30° и , .

Решение:

Сначала найдём поизведение векторов и :

.

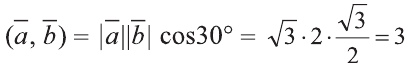
Затем перемножим заданные выражения как многочлены

и, пользуясь распределительным свойством умножения

вектора на число, получим:

.

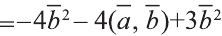
Учитывая, что ,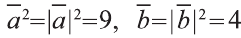

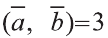
найдём искомое произведение

Преобразование и подобие в пространстве

Геометрические преобразования в пространстве

Если каждую точку заданной в пространстве фигуры F изменить одним и тем же способом, то получим фигуру F_1. Если при этом преобразовании различные точки первой фигуры переходят в различные точки второй, то говорят о преобразовании геометрической фигуры.

Если рассматривать все пространства как геометрическую фигуру, то также можно говорить о преобразовании геометрической фигуры.

Понятие геометрического преобразование в пространстве вводят также как на плоскости. Следовательно, свойства некоторых рассматриваeмых ниже видов преобразований и их доказательства также подобны соответствующим им на плоскости. Поэтому, мы не будем доказывать их и рекомендуем провести их самостоятельно.

Движение и параллельный перенос

Преобразование фигур, при котором сохраняются расстояния между точками, называют движением. Можно привести следующие свойства движения. При движении прямая переходит в прямую, луч — в луч, отрезок — в равный ему отрезок, угол — в равный ему угол, треугольник — в равный ему треугольник, плоскость — в плоскость, тетраэдр — в равный ему тетраэдр.

В пространстве фигуры, которые можно перевести одну в другую при некотором движении называют равными фигурами.

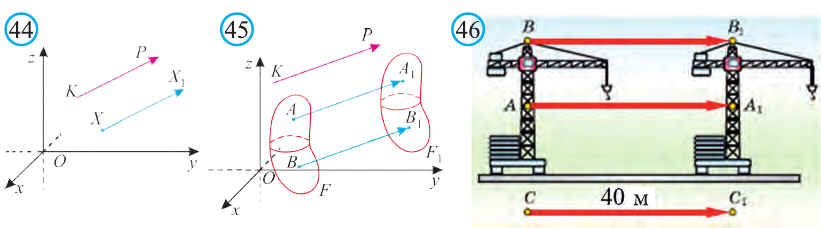
Простейшим примером движения является параллельный перенос.

Пусть в пространстве даны вектор и произвольная точка Х

(рис. 44). Говорят, что точка Х перешла в точку X₁ параллельным

переносом на вектор , если выполняется условие . Если каждую точку фигуры F сдвинуть на вектор при помощи параллельного переноса (рис. 45), то получим фигуру F₁. Тогда говорят, что фигура F получена параллельным переносом фигуры F₁ . При параллельном переносе каждая точка фигуры F сдвигается в одном и том же направлении на одно и то же расстояние.

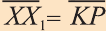
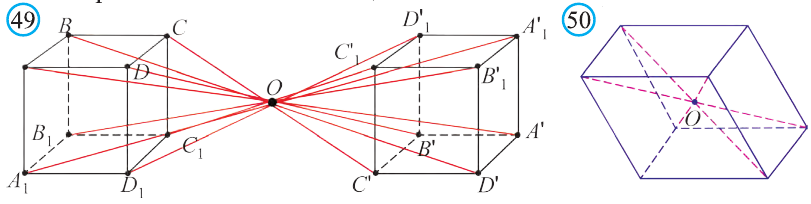
Каждая точка подъёмного крана, изображённого на рисунке 46, параллельно перенесена на 40 м относительно начального положения.

Ясно, что параллельный перенос является движением. Поэтому прямая переходит в прямую, луч — в луч, плоскость — в плоскость,

Пусть точка 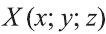фигуры F перешла в точку

фигуры F₁ при помощи параллельного переноса

на вектор .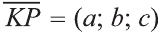

Тогда по определению получим:

или

.

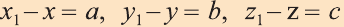
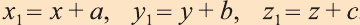
Эти равенства называют формулами параллельного переноса.

Пример:

В какую точку перейдёт точка Р (-2; 4; 6) при параллельном переносе на вектор 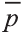= (3; 2; 5)?

Решение:

По вышеприведённым формулам параллельного переноса: .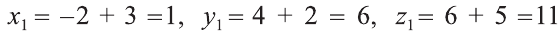

Ответ: .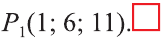

Центральная симметрия в пространстве

Если в пространстве 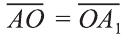, то есть точка О — середина отрезка АА₁ то точки А и А₁ называют симметричными относительно точки О.

Если в пространстве каждая точка фигуры F переходит в точку, симметричную относительно точки О (рис. 47), то такое преобразование называют симметрией относительно точки О. На рисунках 48, 49 изображёны фигуры симметричные относительно точки О. Симметрия относительно точки является движением.

Если при симметрии относительно точки О фигура F переходит в себя, то её называют центрально симметричной фигурой.

Например, диагонали параллелепипеда (рис. 50) относительно их точки пересечения О являются центрально симметричными фигурами.

Пример:

В какую точку перейдет точка A = (1; 2; 3) при симметрии относительно точки О (2; 4; 6)?

Решение:

Пусть А₁ = (х; у; z) — искомая точка. По определению точка

О — середина отрезка АА₁. Следовательно,

Из этих уравнений получаем:

.

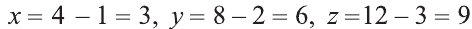
Ответ:

Симметрия относительно плоскости

Точки А и А₁ называют симметричными относительно плоскости а,

если плоскость перпендикулярна отрезку и делит его пополам (рис. 51). Фигуры F₁, и F₂ на рисунке 52 симметричны относительно

плоскости а. Очевидно, что наш силуэт и его отражение симметричны относительно плоскости зеркала (рис. 53).

Симметрия относительно плоскости а является движением.

Поэтому при симметрии относительно плоскости а отрезок переходит в равный ему отрезок, прямая — в прямую, плоскость — в плоскость.

Если при симмeтрии относительно плоскости фигура F переходит в себя, то её называют фигурой симметричной относительно плоскости.

Например, изображённый на рисунке 54 куб, есть фигура, симметричная относительно плоскости а, проходящей через его диагонали АА₁ и СС₁.

Поворот и симметрия относительно оси

Пусть в пространстве заданы точки А и А₁ и прямая l. Если перпендикуляры АК и А₁К, опущенные на прямую l, равны и образуют угол , то говорят, что точка А перешла в точку А₁ в результате поворота на угол относительно прямой l (рис. 55).

Если каждую точку фигуры F повернуть на угол относительно прямой l, то получим новую фигуру F₁ . Тогда говорят, что фигура F перешла в фигуру F₁ с помощью поворота на угол относительно прямой l. На рисунке 56 мы видим фигуры, полученные таким поворотом. Например, повернув куб, изображённый на рисунке 57, на 180° относительно прямой l, получим новый куб.

Поворот относительно прямой также является движением.

Поворот на 180° относительно прямой l называют симметрией относительно прямой l.

Центр, ось и плоскость симметрии называют элементами симметрии. Точки, симметричные точке А (х; у; z) относительно координатных плоскостей, координатных осей и начала координат, будут иметь следующие координаты:

Симметрия в природе и технике

В природе на каждом шагу можно встретить симметрию.

Например, множество живых существ, в частности тела человека и животных, листья растений и цветы устроены симметрично (рис. 58). Также в неживой природе есть элементы, например, снежинки, кристаллы соли. Молекулярное строение веществ тоже состоит из симметричных фигур. Это, конечно, неспроста, поскольку симметричные фигуры не только красивы, но и самые устойчивые.

Раз так, то можно считать, что красота и совершенство природы построены на основе симметрии. Взяв за основу природную красоту и совершенство, строители, инженеры и архитекторы создают строения и механизмы, здания и сооружения, технику и транспортные средства симметричными. В этой работе им очень помогает наука геометрия.

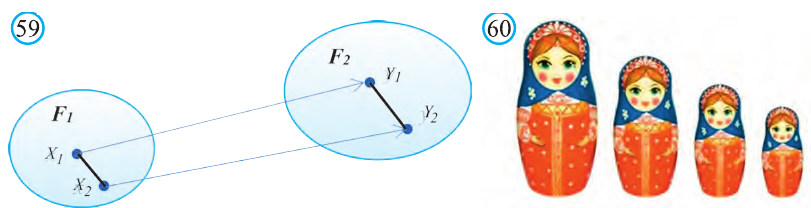
Подобие пространственных фигур

Пусть 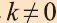и преобразование переводят фигуру F₁, в фигуру F₂. Если

при этом преобразовании для произвольных точек X₁ и Х₂ фигуры F₁ и соответствующих им точек Y₁ и Y₂ фигуры 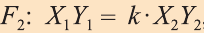, то это преобразование называют преобразованием подобия (рис. 59).

Как видим, понятие преобразования подобия в пространстве вводится также как на плоскости. Следовательно, рассматриваемые ниже виды подобия, их свойства и доказательства этих свойств подобны соответствующим на плоскости. Поэтому, мы не будем останавливаться на их доказательствах и рекомендуем провести их самостоятельно. Преобразование подобия в пространстве отображает прямую в прямую, луч в луч, отрезок в отрезок и угол в угол. Точно также это преобразование плоскость отображает в плоскость.

Если в пространстве одна из фигур перешла в другую с помощью преобразования подобия, то эти фигуры называют подобными.

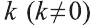
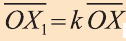
Пусть в пространстве задана фигура F, точка О и число к . Преобразование, переводящее произвольную точку X фигуры F в точку Х₁ удовлетворяющую условию , называют гомотетией относительно центра О с коэффициентом (рис. 61). Точку О называют центром гомотетии, а число коэффициентом гомотетии. Если в результате такого преобразования каждой точки фигуры F получена фигура F₁ то говорят, что фигура F гомотетична фигуре F₁.

Вы видите, что определение гомотетии в пространстве аналогично соответствующему определению на плоскости. Следовательно, все свойства и их доказательства аналогичны. Поэтому, мы не будем доказывать их и рекомендуем провести их самостоятельно.

Гомотетия относительно точки О с коэффициентом является преобразованием подобия. Гомотетия с отличным от нуля коэффициентом при = 1 отображает фигуру F в себя, а при =-1 в фигуру F₁ симметричную фигуре F относительно точки О. В остальных случаях гомотетии не сохраняет расстояния между точками, т. е. не является движением. В результате гомотетии расстояние между точками увеличивается в одно и тоже число раз, т. е. меняются измерения фигуры, но сохраняется её форма. При гомотетии а) прямая отображается в параллельную ей прямую (рис. 62.а); b) плоскость — в параллельную ей плоскость (рис. 62.b), если они не проходят через центр гомотетии.

Если же прямая или плоскость проходят через центр гомотетии, то они отображаются в себя.

• Иррациональные числа
• Действительные числа
• Решение уравнений высших степеней
• Системы неравенств
• Уравнения и неравенства
• Уравнения и неравенства содержащие знак модуля
• Уравнение
• Метод математической индукции

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Telegram и логотип telegram являются товарными знаками корпорации Telegram FZ-LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

📺 Видео

11. Прямая в пространстве и ее уравненияСкачать

Геометрия 11 класс: Сфера и шар. Уравнение сферы. Площадь сферыСкачать

Расстояние от точки до плоскости / Вывод формулыСкачать

Расстояние между двумя точками с заданными координатамиСкачать

Метод координат для ЕГЭ с нуля за 30 минут.Скачать

Расстояние между двумя точками | МатематикаСкачать

РАССТОЯНИЕ МЕЖДУ ТОЧКАМИ 10 и 11 классСкачать

Аналитическая геометрия, 5 урок, Уравнение плоскостиСкачать

Расстояние между точками по координатам.Скачать

Уравнение прямой в пространстве через 2 точки. 11 класс.Скачать

Математика без Ху!ни. Взаимное расположение прямой и плоскости.Скачать

Геометрия. 10 класс. Расстояние между точками /16.02.2021/Скачать