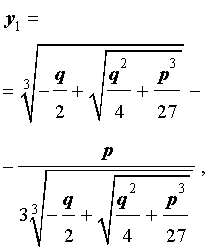
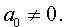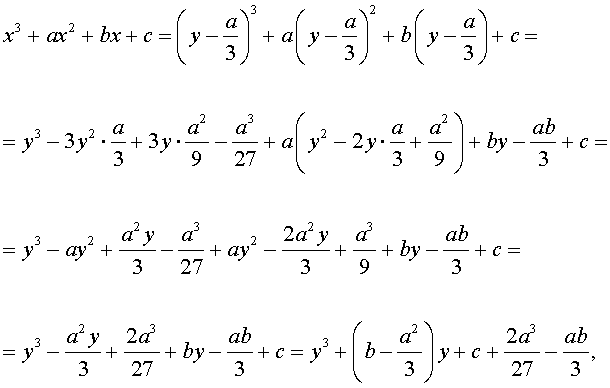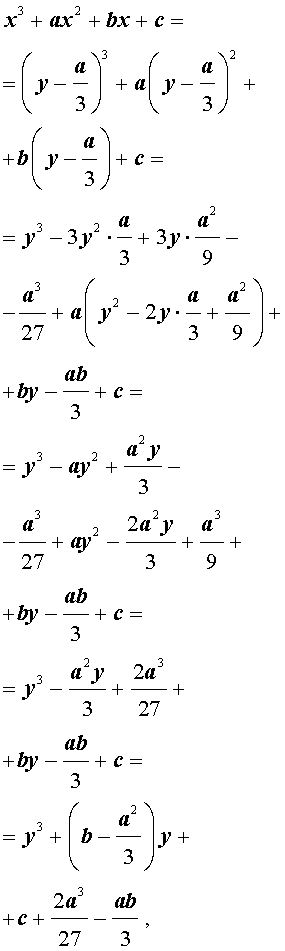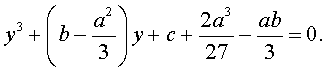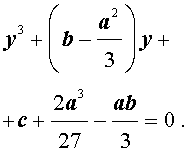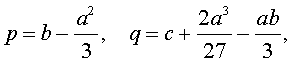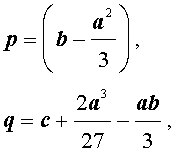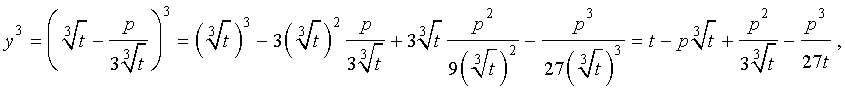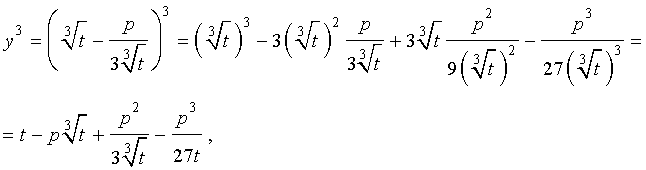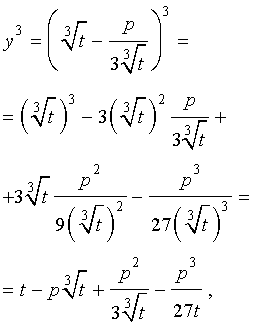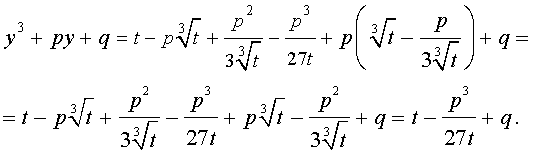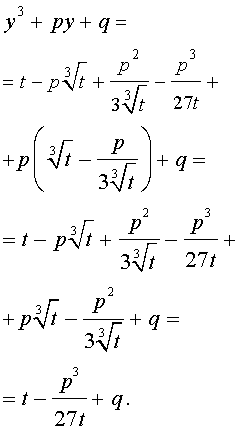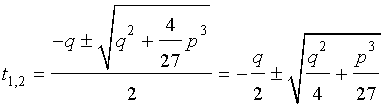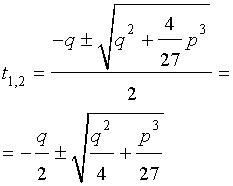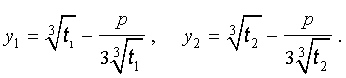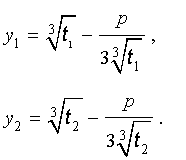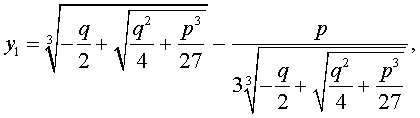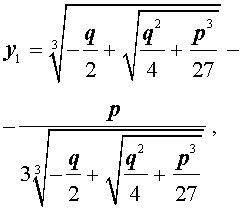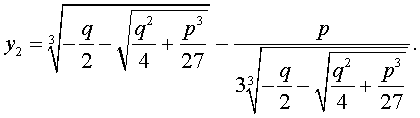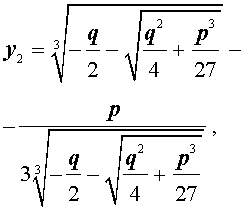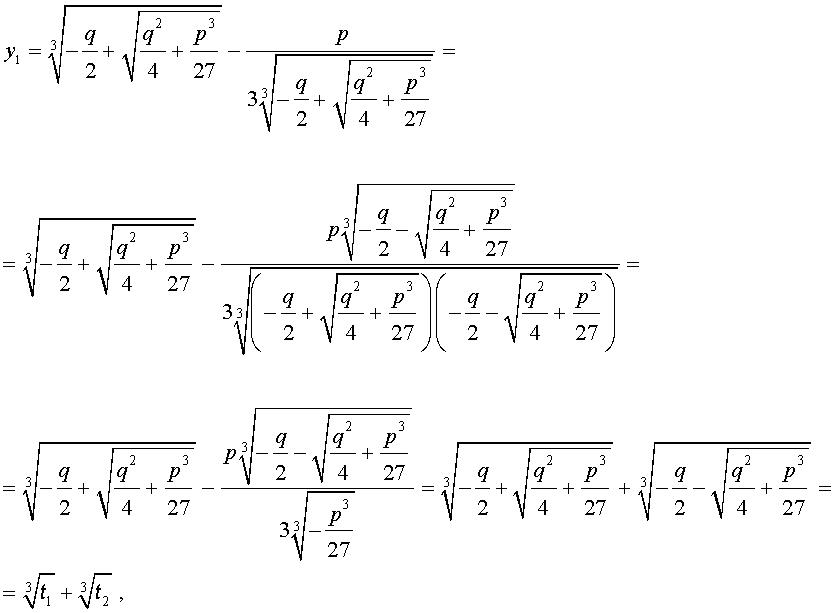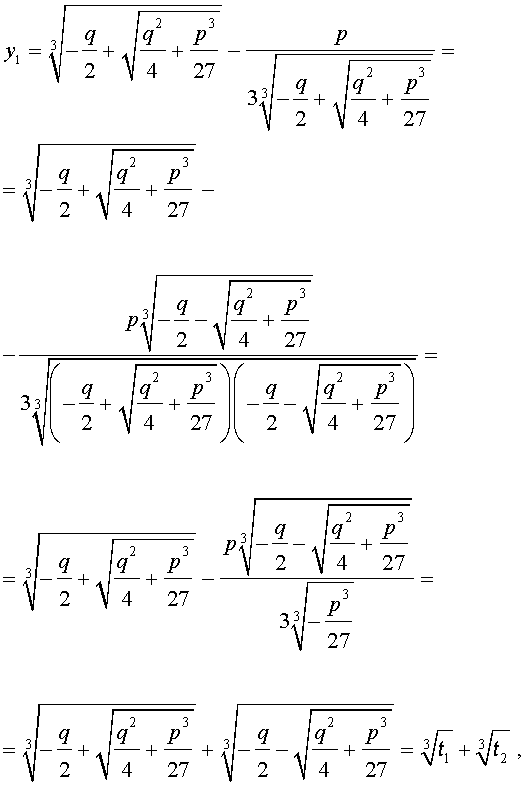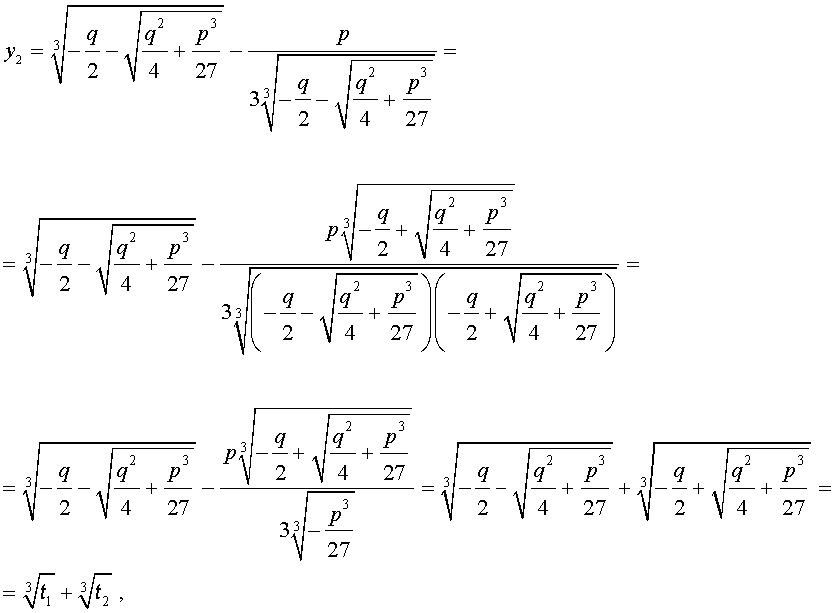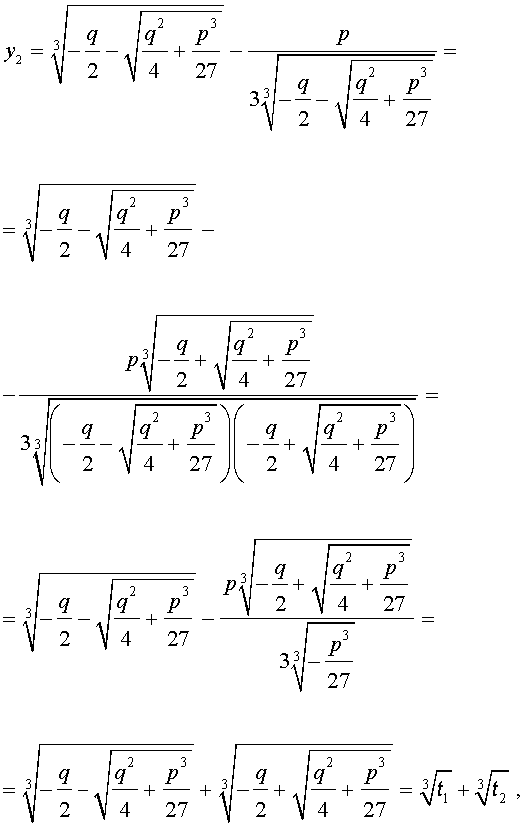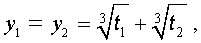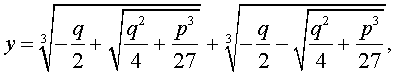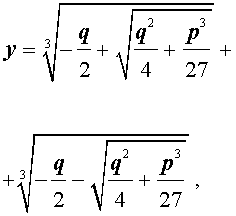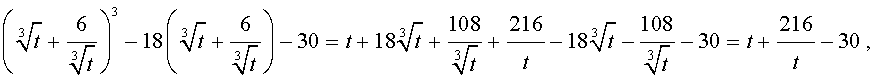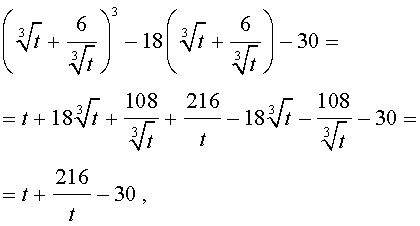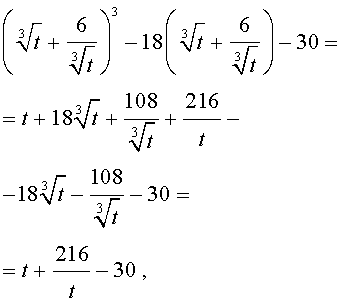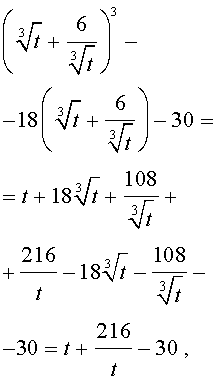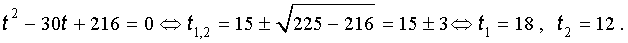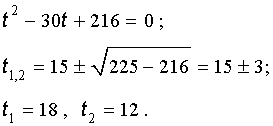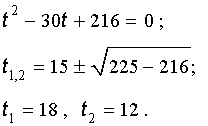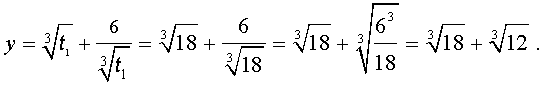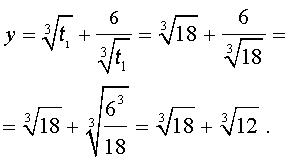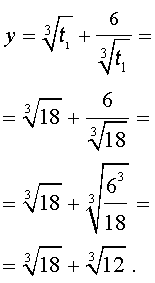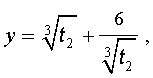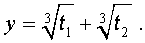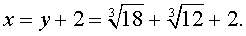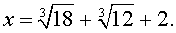Кубическое уравнение— это уравнение вида:
Данный калькулятор предназначен для решения кубических уравнений. В его основе лежит формула Кардано, однако различные частные случаи кубических уравнений (когда один или несколько коэффициентов равны нулю или между коэффициентами присуствует некоторая зависимость и т.д.) решаются более простым путем.
В калькулятор можно вводить как числа и дроби, так и параметры. Коэффициент при x 3 не может быть равен нулю. Ввод уравнения в калькулятор осуществляется в естественном формате. Для ввода десятичных цифр используйте точку в качестве разделителя целой и дробной частей, например 1.45.
- Решение кубических уравнений онлайн
- Как решить кубическое уравнение?
- Решение кубических уравнений. Формула Кардано
- Схема метода Кардано
- Приведение кубических уравнений к трехчленному виду
- Сведение трёхчленных кубических уравнений к квадратным уравнениям при помощи метода Никколо Тартальи
- Формула Кардано
- Пример решения кубического уравнения
- 📽️ Видео
Видео:✓ Как решать кубические уравнения. Формула Кардано | Ботай со мной #025 | Борис ТрушинСкачать
Решение кубических уравнений онлайн
Онлайн калькулятор для подробного решения кубических уравнений
Решение кубического уравнения (уравнения третьего порядка) на нашем сайте производится по методу Виета-Кардано. С помощью ряда формул находятся кубические корни x1, x2 и x3. При вычислении результатов корни могут получиться вещественными или комплексными в зависимости от значения S.
Кубическое уравнение имеет вид ax 3 + bx 2 + cx + d = 0, где
a, b ,c, d – некоторые числа, причём a не равно нулю (a ≠ 0).
x 3 + x 2 + x + = 0 Решить
Как решить кубическое уравнение?
Последовательность решения кубического уравнения вида x 3 +a·x 2 +b·x+c=0:
(воспользуемся тригонометрической формулой Виета)
1. Для начала необходимо вычислить значения Q, R, S по формулам:
Q = (a 2 — 3 · b) / 9
R = (2 · a 3 — 9 · a · b + 27 · c) / 54
S = Q 3 — R 2
Если S > 0, то уравнение будет иметь три действительных корня.
2. Вычисляем параметр φ:
φ = (1 / 3) · arccos (R / √ Q 3 )
3. Находим корни кубического уравнения по формулам:
x1 = -2 · √ Q · cos (φ) — a / 3,
x2 = -2 · √ Q · cos (φ + 2 · π / 3) — a / 3,
x3 = -2 · √ Q · cos (φ — 2 · π / 3) — a / 3,
4. Если получится S 0 уравнение будет иметь один действительный и два комплексных корня, а при Q of your page —>
Видео:Математика | Кубические уравнения по методу СталлонеСкачать
Решение кубических уравнений. Формула Кардано
 Схема метода Кардано |
| Приведение кубических уравнений к трехчленному виду |
| Сведение трёхчленных кубических уравнений к квадратным уравнениям при помощи метода Никколо Тартальи |
| Формула Кардано |
| Пример решения кубического уравнения |
Видео:ФОРМУЛА КАРДАНО-ТАРТАЛЬЯ + РЕКЛАМА МФТИ!!!Скачать
Схема метода Кардано
Целью данного раздела является вывод формулы Кардано для решения уравнений третьей степени ( кубических уравнений )
| a0x 3 + a1x 2 + + a2x + a3= 0, | (1) |
где a0, a1, a2, a3 – произвольные вещественные числа, 
Вывод формулы Кардано состоит из двух этапов.
На первом этапе кубические уравнения вида (1) приводятся к кубическим уравнениям, у которых отсутствует член со второй степенью неизвестного. Такие кубические уравнения называют трёхчленными кубическими уравнениями .
На втором этапе трёхчленные кубические уравнения решаются при помощи сведения их к квадратным уравнениям.
Видео:Решение уравнений третьей степени (формула Кардано)Скачать
Приведение кубических уравнений к трехчленному виду
Разделим уравнение (1) на старший коэффициент a0 . Тогда оно примет вид
| x 3 + ax 2 + bx + c = 0, | (2) |
где a, b, c – произвольные вещественные числа.
Заменим в уравнении (2) переменную x на новую переменную y по формуле:
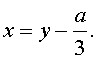 | (3) |
то уравнение (2) примет вид
В результате уравнение (2) примет вид
Если ввести обозначения
то уравнение (4) примет вид
| y 3 + py + q= 0, | (5) |
где p, q – вещественные числа.
Уравнения вида (5) и являются трёхчленными кубическими уравнениями , у которых отсутствует член со второй степенью неизвестного.
Первый этап вывода формулы Кардано завершён.
Видео:Формула Кардано для решения кубических уравненийСкачать
Сведение трёхчленных кубических уравнений к квадратным уравнениям при помощи метода Никколо Тартальи
Следуя методу, примененому Никколо Тартальей (1499-1557) для решения трехчленных кубических уравнений, будем искать решение уравнения (5) в виде
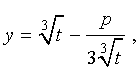 | (6) |
где t – новая переменная.
то выполнено равенство:
Следовательно, уравнение (5) переписывается в виде
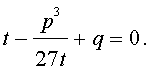 | (7) |
Если теперь уравнение (7) умножить на t , то мы получим квадратное уравнение относительно t :
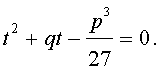 | (8) |
Видео:Формула Кардано. Решение уравнений третьей степени.Скачать
Формула Кардано
Решение уравнения (8) имеет вид:
В соответствии с (6), отсюда вытекает, что уравнение (5) имеет два решения:
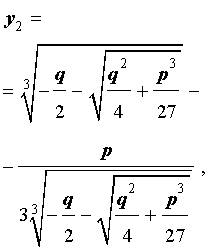
В развернутой форме эти решения записываются так:
Покажем, что, несмотря на кажущиеся различия, решения (10) и (11) совпадают.
С другой стороны,
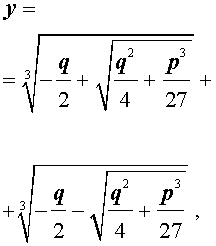
и для решения уравнения (5) мы получили формулу
которая и называется «Формула Кардано» .
Замечание . Поскольку у каждого комплексного числа, отличного от нуля, существуют три различных кубических корня, то, для того, чтобы избежать ошибок при решении кубических уравнений в области комплексных чисел, рекомендуется использовать формулу Кардано в виде (10) или (11).
Видео:Формула Кардано. Ч. 1.Скачать
Пример решения кубического уравнения
Пример . Решить уравнение
| x 3 – 6x 2 – 6x – 2 = 0. | (13) |
Решение . Сначала приведем уравнение (13) к трехчленному виду. Для этого в соответствии с формулой (3) сделаем в уравнении (13) замену
| x = y + 2. | (14) |
Следовательно, уравнение (13) принимает вид
| y 3 – 18y – 30 = 0. | (15) |
Теперь в соответствии с формулой (6) сделаем в уравнении (15) еще одну замену
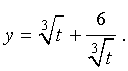 | (16) |
то уравнение (15) примет вид
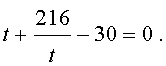 | (17) |
Далее из (17) получаем:
Отсюда по формуле (16) получаем:
Заметим, что такое же, как и в формуле (18), значение получилось бы, если бы мы использовали формулу
или использовали формулу
Далее из равенства (18) в соответствии с (14) получаем:
Таким образом, мы нашли у уравнения (13) вещественный корень
Замечание 1 . У уравнения (13) других вещественных корней нет.
Замечание 2 . Поскольку произвольное кубическое уравнение в комплексной области имеет 3 корня с учетом кратностей, то до полного решения уравнения (13) остается найти еще 2 корня. Эти корни можно найти разными способами, в частности, применив вариант формулы Кардано для области комплексных чисел. Однако применение такого варианта формулы Кардано значительно выходит за рамки курса математики даже специализированных математических школ.
📽️ Видео
КАК РЕШАТЬ КУБИЧЕСКИЕ УРАВНЕНИЯ | Разбираем на конкретном примереСкачать
Формула Кардано для решения кубического уравнения (Открытая часть сз кафедры математики)Скачать
Как решать дробно-рациональные уравнения? | МатематикаСкачать
Решение уравнения третьей степени x³-9x-12=0Скачать
Решение кубического уравнения общего вида, используя комплексные числа, по формуле Кардано!Скачать
Формула Кардано - Тартальи// Почему выглядит именно так?Скачать
Кубические уравнения. Деление столбиком. Схема Горнера.Скачать
Комплексные числа: коротко и понятно – Алексей Савватеев | Лекции по математике | НаучпопСкачать
Самый простой способ решить кубическое уравнениеСкачать
Теорема Виета для многочлена 3 порядка. 10 класс.Скачать
Мнимые числа реальны: #1-13 [Welch Labs]Скачать
![Мнимые числа реальны: #1-13 [Welch Labs]](https://i.ytimg.com/vi/kicp_odjsRs/0.jpg)
КУБИЧЕСКИЕ УРАВНЕНИЯ 😉 #егэ #математика #профильныйегэ #shorts #огэСкачать
Можно ли решить уравнение 5-й степени? – математик Алексей Савватеев | НаучпопСкачать
