Формула для решения уравнения tgx a (5 видео)

Содержание

Арктангенс и решение уравнения tg x=a (продолжение)
Решение уравнения tg x = а
Простейшие тригонометрические уравнения с тангенсом и котангенсом
Алгоритм решения простейших уравнений с тангенсом
Алгоритм решения простейших уравнений с котангенсом
🎥 Видео

Видео:Как решать tgx=aСкачать

Арктангенс и решение уравнения tg x=a (продолжение)

Этот видеоурок доступен по абонементу

У вас уже есть абонемент? Войти

На этом уроке мы продолжим изучение арктангенса и решение уравнений вида tg x = a для любого а. В начале урока решим уравнение с табличным значением и проиллюстрируем решение на графике, а потом и на круге. Далее решим уравнение tgx = aв общем виде и выведем общую формулу ответа. Проиллюстрируем вычисления на графике и на круге и рассмотрим различные формы ответа. В конце урока решим несколько задач с иллюстрацией решений на графике и на круге.

Видео:Решение уравнений вида tg x = a и ctg x = aСкачать

Решение уравнения tg x = а

Корни уравнения tg(x) = a выражаются формулой x=arctg(a)+πn, n ∈ Z.

Попробуем разобраться, почему, решения выражаются этой формулой.

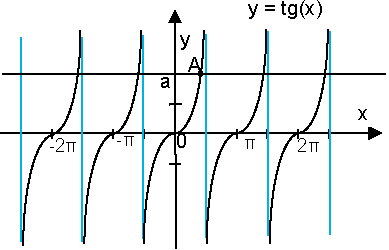
Проще всего это сделать, посмотрев на график функции y = tg(x).

Корни этого уравнения – это абсциссы точек пересечения прямой y = a. Начертим на одной плоскости график функции y = tg(x) и график функции y = a.

По рисунку видно, что абсцисса точки А – это arctg(a), остальные точки пересечения имеют абсциссы x=arctg(a)+πn, n ∈ Z.

Решить уравнение tg(2x) = 1.

По формуле, приведенной выше, имеем 2x = arctg(1)+πn, n ∈ Z.

Известно, что arctg(1) = π/4, значит 2x = π/4+πn, n ∈ Z, x = π/8+1/2πn, n ∈ Z.

Ошибка в тексте? Выдели её мышкой и нажми

Остались рефераты, курсовые, презентации? Поделись с нами — загрузи их здесь!

Видео:Уравнение tgx = aСкачать

Простейшие тригонометрические уравнения с тангенсом и котангенсом

Чтобы уверенно решать простейшие уравнения с тангенсом или котангенсом нужно знать значения стандартных точек на круге и стандартные значения на осях тангенсов и котангенсов (если в этом материале есть пробелы, читайте « Как запомнить тригонометрический круг »).

Видео:уравнение tgx=aСкачать

Алгоритм решения простейших уравнений с тангенсом

Давайте с вами рассмотрим типичное уравнение, например, (tg⁡x=sqrt).

Пример. Решить уравнение (tg⁡x=sqrt).

Чего от нас здесь хотят? Чтобы мы написали все такие значения угла в Пи, для которых тангенс равен корню из трех. Причем написать надо именно все такие углы. Давайте нарисуем тригонометрический круг и ось тангенсов…

…и обозначим то место на оси, куда мы должны попасть в итоге.

Теперь найдем через какие точки на окружности мы должны идти, чтобы попасть в этот самый корень из трех –проведем прямую через начало координат и найденную точку на оси тангенсов.

Точки найдены. Давайте подпишем значение одной из них…

…и запишем окончательный ответ – все возможные варианты значений в Пи, находящиеся в отмеченных точках: (x=frac+πn), (n∈Z).

Замечание. Вы, наверно, обратили внимание, что в отличие от уравнений с синусом и косинусом , здесь записывается только одна серия корней, причем в формуле добавляется (πn), а не (2πn). Дело в том, что в любом уравнении с тангенсом решением получаются две точки на окружности, которые находятся друг от друга на расстоянии (π). Благодаря этому значение обеих точек можно записать одной формулой в виде (x=t_0+πn), (n∈Z).

Пример. Решить уравнение (tg⁡x=-1).

Итак, окончательный алгоритм решения подобных задач выглядит следующим образом:

Шаг 1. Построить окружность, оси синусов и косинусов, а также ось тангенсов.

Шаг 2. Отметить на оси тангенсов значение, которому тангенс должен быть равен.

Шаг 3. Соединить прямой линией центр окружности и отмеченную точку на оси тангенсов.

Шаг 4. Найти значение одной из точек на круге.

Шаг 5. Записать ответ используя формулу (x=t_0+πn), (n∈Z) (подробнее о формуле в видео), где (t_0) – как раз то значение, которые вы нашли в шаге 4.

Специально для вас мы сделали удобную табличку со всеми шагами алгоритма и разными примерами к нему. Пользуйтесь на здоровье! Можете даже распечатать и повесить на стенку, чтоб больше никогда не ошибаться в этих уравнениях.

Видео:10 класс. Решение уравнений tg x =aСкачать

Алгоритм решения простейших уравнений с котангенсом

Сразу скажу, что алгоритм решения уравнений с котангенсом почти такой же, как и с тангенсом.

Шаг 1. Вопрос у нас практически тот же – из каких точек круга можно попасть в (frac<sqrt>) на оси котангенсов?
Строим круг, проводим нужные оси.

Теперь отмечаем на оси котангенсов значение, которому котангенс должен быть равен…

…и соединяем центр окружности и точку на оси котангенсов прямой линией.

По сути точки найдены. Осталось записать их все. Вновь определяем значение в одной из них…

…и записываем окончательный ответ по формуле (x=t_0+πn), (n∈Z), потому что у котангенса период такой же как у тангенса: (πn).

Кстати, вы обратили внимание, что ответы в задачах совпали? Здесь нет ошибки, ведь для любой точки круга, тангенс которой равен (sqrt), котангенс будет (frac<sqrt>).

Разберем еще пример, а потом подведем итог.

Пример. Решить уравнение (ctg⁡x=-1). Здесь подробно расписывать не буду, так как логика полностью аналогична вышеизложенной.

Итак, алгоритм решения простейших тригонометрических уравнений с котангенсом:

Шаг 1. Построить окружность и оси синусов и косинусов, а также ось котангенсов.

Шаг 2. Отметить на оси котангенсов значение, которому котангенс должен быть равен.

Шаг 3. Соединить центр окружности и точку на оси котангенсов прямой линией.

Шаг 4. Найти значение одной из точек на круге.

Шаг 5. Записать ответ используя формулу (x=t_0+πn), (n∈Z), где (t_0) – как раз то значение, которые вы нашли в шаге 4. И табличка в награду всем дочитавшим до этого места.

Примечание. Возможно, вы обратили внимание, что при решении примеров 2 и 3 в обеих табличках мы использовали функции (arctg) и (arcctg). Если вы не знаете, что это – читайте эту статью.