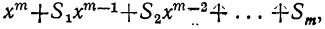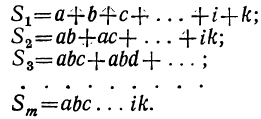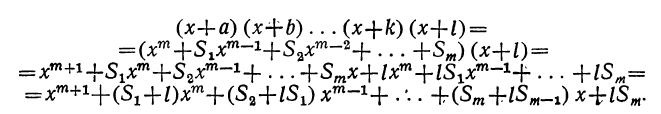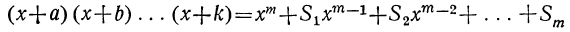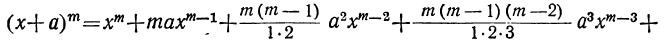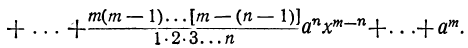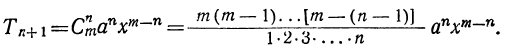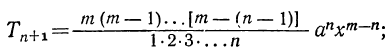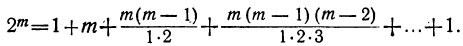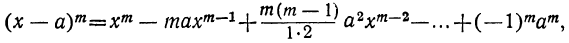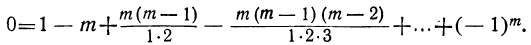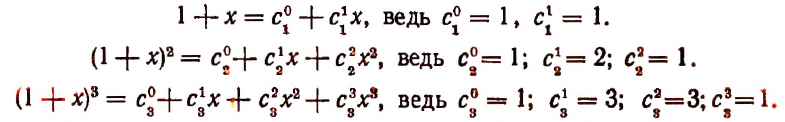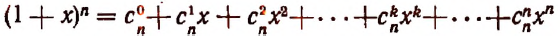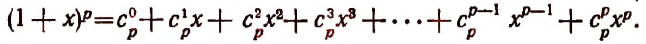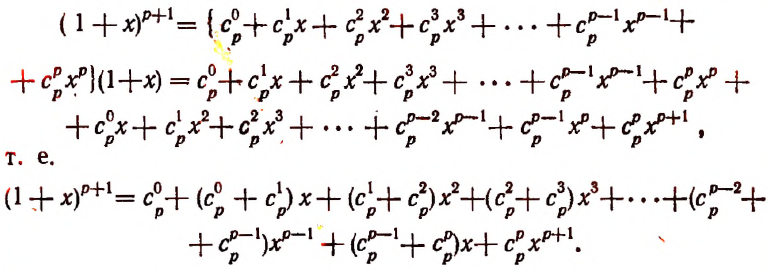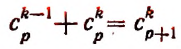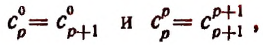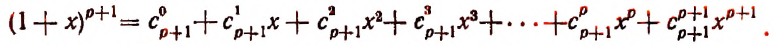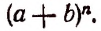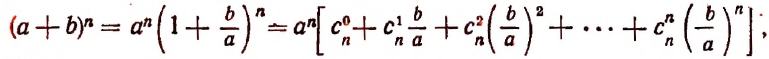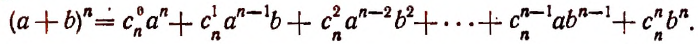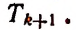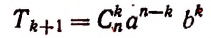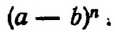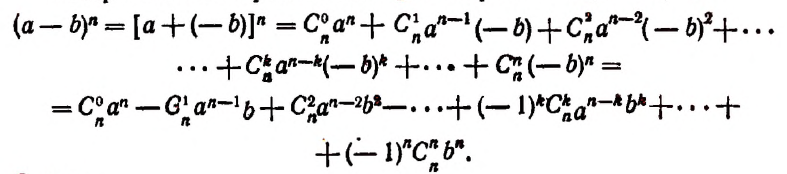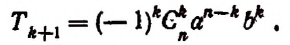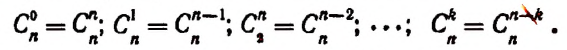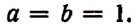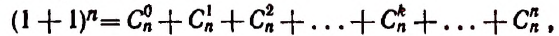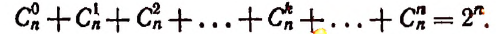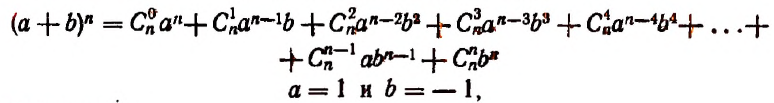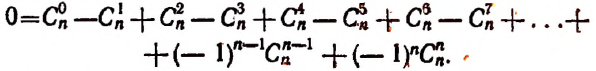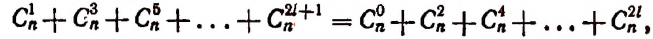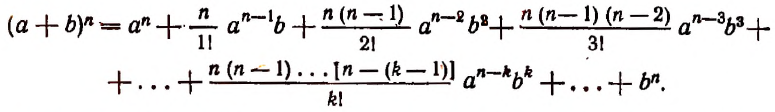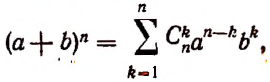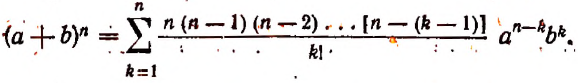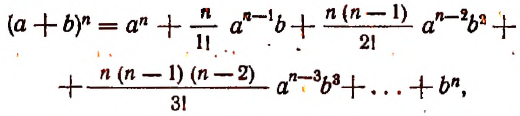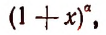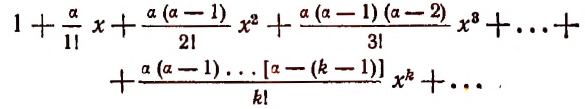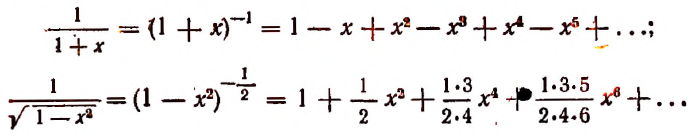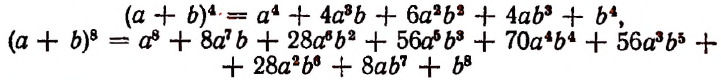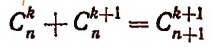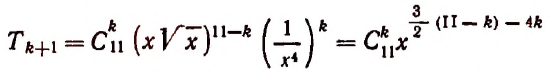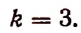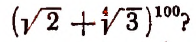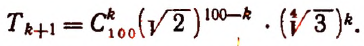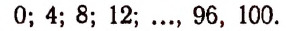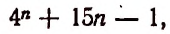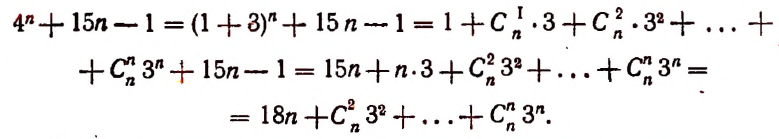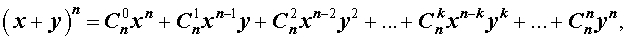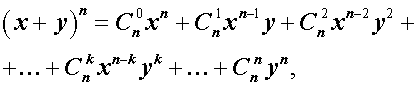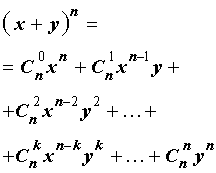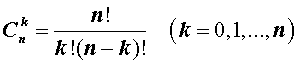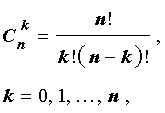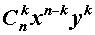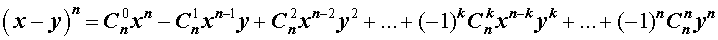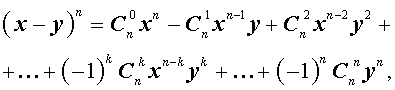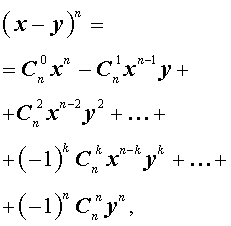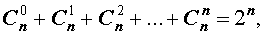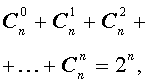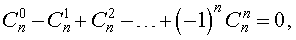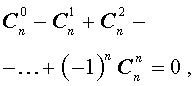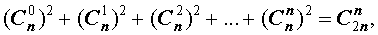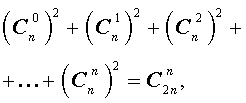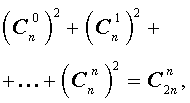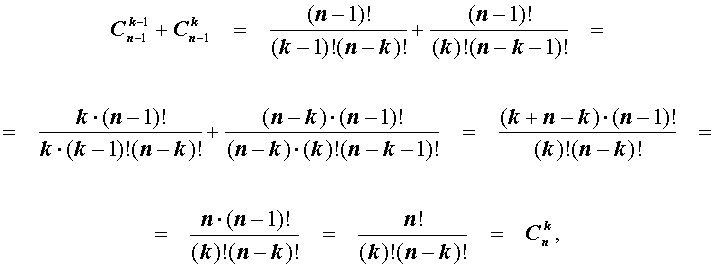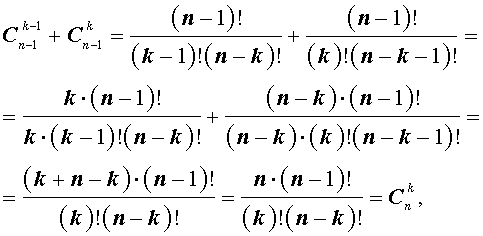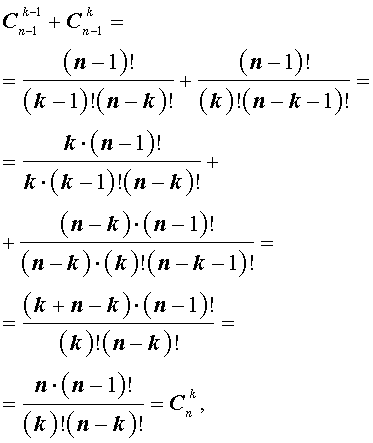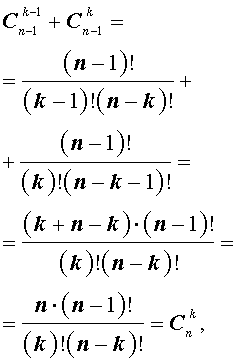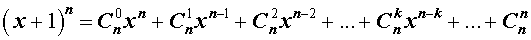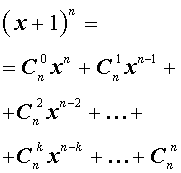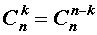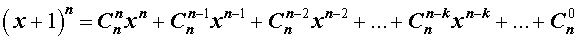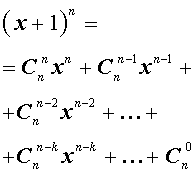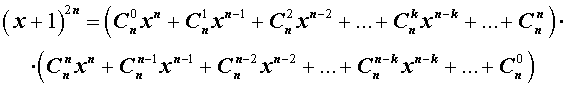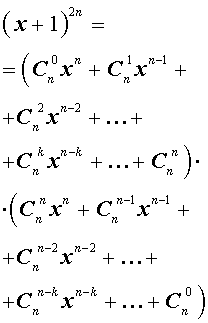- Бином Ньютона — формула
- Коэффициенты бинома Ньютона, свойства биномиальных коэффициентов, треугольник Паскаля
- Доказательство формулы бинома Ньютона
- Бином Ньютона — математическая формула с примером решения и объяснением
- Формула бинома Ньютона
- Свойства формулы бинома Ньютона
- Применение формулы бинома к многочлену
- Вывод формулы бинома ньютона
- Свойства разложения бинома
- Свойства биномиальных коэффициентов
- Арифметический треугольник, или треугольник паскаля
- Примеры с решением на Бином Ньютона
- Дополнение к Бином Ньютону
- Бином Ньютона
- Формула бинома Ньютона
- Связь бинома Ньютона с треугольником Паскаля
- Свойства биномиальных коэффициентов
- 🎦 Видео
Видео:#219. БИНОМ НЬЮТОНА ДЛЯ ЧАЙНИКОВСкачать

Бином Ньютона — формула
С натуральным n формула Бинома Ньютона принимает вид a + b n = C n 0 · a n + C n 1 · a n — 1 · b + C n 2 · a n — 2 · b 2 + . . . + C n n — 1 · a · b n — 1 + C n n · b n , где имеем, что C n k = ( n ) ! ( k ) ! · ( n — k ) ! = n ( n — 1 ) · ( n — 2 ) · . . . · ( n — ( k — 1 ) ) ( k ) ! — биномиальные коэффициенты, где есть n по k , k = 0 , 1 , 2 , … , n , а » ! » является знаком факториала.
В формуле сокращенного умножения a + b 2 = C 2 0 · a 2 + C 2 1 · a 1 · b + C 2 2 · b 2 = a 2 + 2 a b + b 2
просматривается формула бинома Ньютона, так как при n = 2 является его частным случаем.
Первая часть бинома называют разложением ( a + b ) n , а С n k · a n — k · b k — ( k + 1 ) -ым членом разложения, где k = 0 , 1 , 2 , … , n .
Видео:Бином Ньютона максимально простым языкомСкачать

Коэффициенты бинома Ньютона, свойства биномиальных коэффициентов, треугольник Паскаля
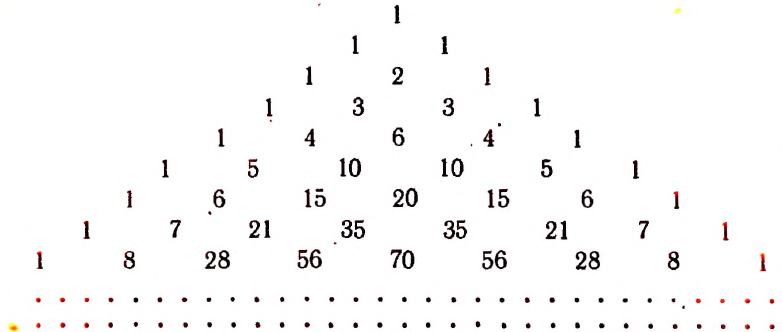
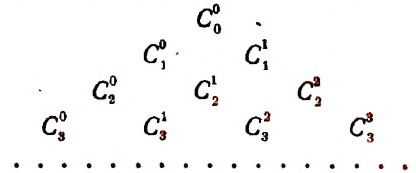
Представление биномиальных коэффициентов для различных n осуществляется при помощи таблицы, которая имеет название арифметического треугольника Паскаля. Общий вид таблицы:
| Показатель степени | Биноминальные коэффициенты | ||||||||||
| 0 | C 0 0 | ||||||||||
| 1 | C 1 0 | C 1 1 | |||||||||
| 2 | C 2 0 | C 2 1 | C 2 2 | ||||||||
| 3 | C 3 0 | C 3 1 | C 3 2 | C 3 3 | |||||||
| ⋮ | … | … | … | … | … | … | … | … | … | ||
| n | C n 0 | C n 1 | … | … | … | … | … | C n n — 1 | C n n | ||
При натуральных n такой треугольник Паскаля состоит из значений коэффициентов бинома:
| Показатель степени | Биноминальные коэффициенты | ||||||||||||||
| 0 | 1 | ||||||||||||||
| 1 | 1 | 1 | |||||||||||||
| 2 | 1 | 2 | 1 | ||||||||||||
| 3 | 1 | 3 | 3 | 1 | |||||||||||
| 4 | 1 | 4 | 6 | 4 | 1 | ||||||||||
| 5 | 1 | 5 | 10 | 10 | 5 | 1 | |||||||||
| ⋮ | … | … | … | … | … | … | … | … | … | … | … | … | … | ||
| n | C n 0 | C n 1 | … | … | … | … | … | … | … | … | … | C n n — 1 | C n n | ||
Боковые стороны треугольника имеют значение единиц. Внутри располагаются числа, которые получаются при сложении двух чисел соседних сторон. Значения, которые выделены красным, получают как сумму четверки, а синим – шестерки. Правило применимо для всех внутренних чисел, которые входят в состав треугольника. Свойства коэффициентов объясняются при помощи бинома Ньютона.
Видео:Бином Ньютона. 10 класс.Скачать

Доказательство формулы бинома Ньютона
Имеются равенства, которые справедливы для коэффициентов бинома Ньютона:
- коэффициента располагаются равноудалено от начала и конца, причем равны, что видно по формуле C n p = C n n — p , где р = 0 , 1 , 2 , … , n ;
- C n p = C n p + 1 = C n + 1 p + 1 ;
- биномиальные коэффициенты в сумме дают 2 в степени показателя степени бинома, то есть C n 0 + C n 1 + C n 2 + . . . + C n n = 2 n ;
- при четном расположении биноминальных коэффициентов их сумма равняется сумме биномиальных коэффициентов, расположенных в нечетных местах.
Равенство вида a + b n = C n 0 · a n + C n 1 · a n — 1 · b + C n 2 · a n — 2 · b 2 + . . . + C n n — 1 · a · b n — 1 + C n n · b n считается справедливым. Докажем его существование.
Для этого необходимо применить метод математической индукции.
Для доказательства необходимо выполнить несколько пунктов:
- Проверка справедливости разложения при n = 3 . Имеем, что
a + b 3 = a + b a + b a + b = a 2 + a b + b a + b 2 a + b = = a 2 + 2 a b + b 2 a + b = a 3 + 2 a 2 b + a b 2 + a 2 b + 2 a b + b 3 = = a 3 + 3 a 2 b + 3 a b 2 + b 3 = C 3 0 a 3 + C 3 1 a 2 b + C 3 2 a b 2 + C 3 3 b 3 - Если неравенство верно при n — 1 , тогда выражение вида a + b n — 1 = C n — 1 0 · a n — 1 · C n — 1 1 · a n — 2 · b · C n — 1 2 · a n — 3 · b 2 + . . . + C n — 1 n — 2 · a · b n — 2 + C n — 1 n — 1 · b n — 1
- Доказательство равенства a + b n — 1 = C n — 1 0 · a n — 1 · C n — 1 1 · a n — 2 · b · C n — 1 2 · a n — 3 · b 2 + . . . + C n — 1 n — 2 · a · b n — 2 + C n — 1 n — 1 · b n — 1 , основываясь на 2 пункте.
Доказательство 1
a + b n = a + b a + b n — 1 = = ( a + b ) C n — 1 0 · a n — 1 · C n — 1 1 · a n — 2 · b · C n — 1 2 · a n — 3 · b 2 + . . . + C n — 1 n — 2 · a · b n — 2 + C n — 1 n — 1 · b n — 1
Необходимо раскрыть скобки, тогда получим a + b n = C n — 1 0 · a n + C n — 1 1 · a n — 1 · b + C n — 1 2 · a n — 2 · b 2 + . . . + C n — 1 n — 2 · a 2 · b n — 2 + + C n — 1 n — 1 · a · b n — 1 + C n — 1 0 · a n — 1 · b + C n — 1 1 · a n — 2 · b 2 + C n — 1 2 · a n — 3 · b 3 + . . . + C n — 1 n — 2 · a · b n — 1 + C n — 1 n — 1 · b n
Производим группировку слагаемых
a + b n = = C n — 1 0 · a n + C n — 1 1 + C n — 1 0 · a n — 1 · b + C n — 1 2 + C n — 1 1 · a n — 2 · b 2 + . . . + + C n — 1 n — 1 + C n — 1 n — 2 · a · b n — 1 + C n — 1 n — 1 · b n
Имеем, что C n — 1 0 = 1 и C n 0 = 1 , тогда C n — 1 0 = C n 0 . Если C n — 1 n — 1 = 1 и C n n = 1 , тогда C n — 1 n — 1 = C n n . При применении свойства сочетаний C n p + C n p + 1 = C n + 1 p + 1 , получаем выражение вида
C n — 1 1 + C n — 1 0 = C n 1 C n — 1 2 + C n — 1 1 = C n 2 ⋮ C n — 1 n — 1 + C n — 1 n — 2 = C n n — 1
Произведем подстановку в полученное равенство. Получим, что
a + b n = = C n — 1 0 · a n + C n — 1 1 + C n — 1 0 · a n — 1 · b + C n — 1 2 + C n — 1 1 · a n — 2 · b 2 + . . . + + C n — 1 n — 1 + C n — 1 n — 2 · a · b n — 1 = C n — 1 n — 1 · b n
После чего можно переходить к биному Ньютона, тогда a + b n = C n 0 · a n + C n 1 · a n — 1 · b + C n 2 · a n — 2 · b 2 + . . . + C n n — 1 · a · b n — 1 + C n n · b n .
Видео:Бином Ньютона. Практическая часть. 10 класс.Скачать

Бином Ньютона — математическая формула с примером решения и объяснением
Рассматривая эти произведения, замечаем, что все они составлены по одному и тому же закону, а именно:
Произведение составляет многочлен, расположенный по убывающим степеням буквы х.
Показатель первого члена равен числу перемножаемых биномов; показатели при х в следующих членах убывают на 1; последний член не содержит х (содержит его в нулевой степени).
Коэффициент первого члена есть 1; коэффициент второго члена есть сумма всех вторых членов перемножаемых биномов; коэффициент третьего члена есть сумма всех произведений вторых членов, взятых по два; коэффициент четвёртого члена есть сумма всех произведений вторых членов, взятых по три. Последний член есть произведение всех вторых членов.
Докажем, что этот закон применим к произведению какого угодно числа биномов. Для этого предварительно убедимся, что если он верен для произведения m биномов:
(x+a) (x+b) (х+с) … (x+k),
то при этом предположении будет верен и для произведения (m+1) биномов:
(x+a) (x+b) (x+c) . .. (x+k) (х+l).
Итак, допустим, что верно следующее равенство:
(x+α) (x+b) (х+с)… (x+k) =
где для краткости мы положим:
Умножим обе части допущенного равенства на бином x+l:
Рассматривая это новое произведение, убеждаемся, что оно подчиняется такому же закону, какой мы предположили верным для m биномов. Действительно, во-первых, этому закону следуют показатели буквы х; во-вторых, ему же следуют и коэффициенты, так как коэффициент второго члена S+l есть сумма всех вторых членов перемножаемых биномов, включая сюда и l; коэффициент третьего члена S₂+lS₁ есть сумма парных произведений всех вторых членов, включая сюда и l, и т. д.; наконец, 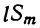
Мы видели, что закон этот верен для произведения двух, трёх и четырёх биномов; следовательно, по доказанному теперь, он должен быть верен и для произведения 4+1, т. е. для произведения пяти биномов, если же он верен для произведения пяти биномов, то он верен и для произведения 5+1, т. е. для произведения шести биномов, и т. д.
Изложенное рассуждение представляет так называемое „доказательство от m к m+1“. Оно называется также „математической индукцией» (или „совершенной индукцией»). Заметим, что в предыдущих главах этой книги неоднократно представлялся случай применить доказательство от m к m + 1 . Мы этого не делали только ради простоты изложения.
Видео:✓ Бином Ньютона. Игра в слова. Числа сочетаний | Комбинаторика | Ботай со мной #057 | Борис ТрушинСкачать

Формула бинома Ньютона
Предположим, что в доказанном нами равенстве
все вторые члены биномов одинаковы, т. е. что a=b=c= … =k. Тогда левая часть будет степень бинома 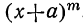
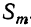
Коэффициент S₁, равный a+b+c+ … +k, обратится в та. Коэффициент S₂, равный ab+ac+ad+ …. обратится в число α², повторённое столько раз, сколько можно составить сочетаний из m элементов по 2, т. е. обратится в 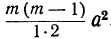
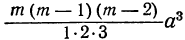
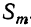
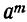
Это равенство известно как формула бинома Ньютона, причём многочлен, стоящий в правой части формулы, называется разложением бинома. Рассмотрим особенности этого многочлена.
Свойства формулы бинома Ньютона
Из этих свойств мы укажем следующие 10:
1) Показатели буквы х уменьшаются на 1 от первого члена к последнему, причём в первом члене показатель х равен показателю степени бинома, а в последнем он есть 0; наоборот, показатели буквы а увеличиваются на 1 от первого члена к последнему, причём в первом члене показатель при а есть 0; а в последнем он равен показателю степени бинома. Вследствие этого сумма показателей при х и а в каждом члене одна и та же, а именно: она равна показателю степени бинома.
2) Число всех членов разложения есть m+1, так как разложение содержит все степени а от 0 до m включительно.
3) Коэффициенты равны: у первого члена — единице, у второго члена — показателю степени бинома, у третьего члена — числу сочетаний из m элементов по 2, у четвёртого члена — числу сочетаний из m элементов по 3; вообще коэффициент (n+1)-ro члена есть число сочетаний из m элементов по n. Наконец, коэффициент последнего члена равен числу сочетаний из т элементов по m, т. е. 1.
Заметим, что эти коэффициенты называются биномиальными.
4) Обозначая каждый член разложения буквой T с цифрой внизу, указывающей номер места этого члена в разложении, т. е. первый член T₁, второй член T₂ и т. д., мы можем написать:
Эта формула выражает общий член разложения, так как из неё мы можем получить все члены (кроме первого), подставляя на место n числа: 1, 2, 3,…. m.
5) Коэффициент первого члена от начала разложения равен единице, коэффициент первого члена от конца тоже равен единице. Коэффициент второго члена от начала есть m, т. е. 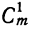
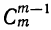
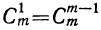
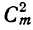
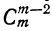
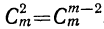
Коэффициенты членов, одинаково удалённых от концов разложения, равны между собой.
6) Рассматривая биномиальные коэффициенты:
мы замечаем, что при переходе от одного коэффициента к следующему числители умножаются на числа, всё меньшие и меньшие (на m—1, на m — 2, на m — 3 и т. д.), а знаменатели умножаются на числа, всё большие и большие (на 2, на 3, на 4 и т. д.). Вследствие этого коэффициенты сначала возрастают (пока множители в числителе остаются большими соответственных множителей в знаменателе), а затем убывают. Так как коэффициенты членов, равно отстоящих от концов разложения, одинаковы, то наибольший коэффициент должен находиться посередине разложения. При этом, если число всех членов разложения нечётное (что бывает при чётном показателе бинома), то посередине будет один член с наибольшим коэффициентом; если же число всех членов чётное (что бывает при нечётном показателе бинома), то посередине должны быть два члена с одинаковыми наибольшими коэффициентами. Например:
(х+α)⁴=x⁴+4αx³+6α²x²+4α³x+α⁴;
(x+α)⁵=x⁵+5αx⁴+10α²x3+10α³x²+5α⁴x+α⁵∙
7) Из сравнения двух рядом стоящих членов: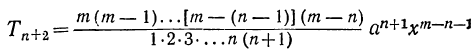
заключаем, что:
Для получения коэффициента следующего члена достаточно умножить коэффициент предыдущего члена на показатель буквы х в этом члене и разделить на число членов, предшествующих определяемому.
Пользуясь этим свойством, можно сразу писать, например, (x+a)⁷=x⁷+7ax⁶+…
Теперь берём 7, умножаем его на 6 и делим на 2, получаем 21: (x+a)⁷=x⁷+7ax⁶+21a²x⁵+… .
Теперь уже выписаны члены до середины ряда, остальные получим, основываясь на свойстве пятом:
(х+а)⁷ =х⁷-7αx⁶+21α²x⁵+35α³x⁴+35α⁴x³+21α⁵x²+7α⁶x+α⁷.
8) Сумма всех биномиальных коэффициентов равна 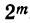
Например, сумма коэффициентов в разложении (х+a)⁷ равна
1+7+21+35+35 +21+7+1 = 128=2⁷.
9) Заменив в формуле бинома а на — а, получим: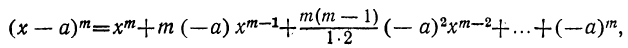
т. е.
следовательно, знаки + и — чередуются.
10) Если в последнем равенстве положим x=α =1, то найдём:
Сумма биномиальных коэффициентов, стоящих на нечётных местах, равна сумме биномиальных коэффициентов, стоящих на чётных местах.
Применение формулы бинома к многочлену
Формула бинома Ньютона позволяет возвышать в степень многочлен. Так:
(α+ b+c)⁴ = [(а+b)+с]⁴= (a+b)⁴+4c (а+b)³+6c² (а+b)²+4c³ (a+b)+c⁴.
Видео:Бином Ньютона: формула, доказательство и Треугольник ПаскаляСкачать

Вывод формулы бинома ньютона
Возникает вопрос, будет ли закономерность, наблюдаемая в этих формулах, обладать общностью, т. е. будет ли справедливой формула
при всяком натуральном значении n?
Воспользуемся методом полной индукции. Допустим, что формула верна для произвольно взятого натурального числа р, т. е. предположим справедливым следующее равенство:
Умножим обе части этого предполагаемого равенства на
и приняв во внимание, что
Из предположения, что формула верна при 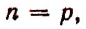
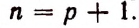
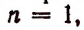
Теперь легко получить разложение и для
Последняя формула и называется формулой бинома Ньютона. Ее правая часть называется разложением степени бинома.
Числа 
Видео:11 класс, 3 урок, Уравнения высших степенейСкачать

Свойства разложения бинома
В разложении бинома содержится членов на один больше, чем показатель степени бинома.
Все члены разложения имеют относительно букв а и b одно и то же измерение, равное показателю степени бинома. (Измерением одночлена относительно букв а и b называется сумма показателей степеней этих букв, входящих в этот одночлен.)
Поскольку все члены разложения имеют одинаковое измерение относительно букв а и b, то это разложение является однородным многочленом относительно букв а и b (см. стр. 450).
В разложении показатель степени буквы а последовательно понижается на единицу, начиная с показателя n, а показатель степени буквы b последовательно повышается на единицу, начиная с показателя, равного нулю.
Член разложения 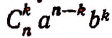
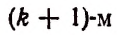
называется формулой общего члена разложения, так как, давая букве k целые значения от 0 до n, мы можем получить из нее любой член разложения.
Теперь напишем разложение для выражения
Видео:Доказательство формулы бинома НьютонаСкачать

Свойства биномиальных коэффициентов
1. Биномиальные коэффициенты, равноудаленные от начала и конца разложения, равны между собой. Действительно, по первому свойству числа сочетаний имеем:
2. Сумма биномиальных коэффициентов равна числу 2, возведенному в степень, равную показателю степени бинома.
Доказательство:
Положим, в формуле бинома
3. Сумма биномиальных коэффициентов, стоящих на четных местах, равна сумме, биномиальных коэффициентов, стоящих на нечетных местах.
Доказательство:
Полагая в тождестве
Перенеся все отрицательные члены в левую часть, получим:
что и требовалось доказать.
Если вместо биномиальных коэффициентов 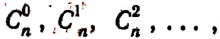

Формулу бинома Ньютона принято записывать ради краткости в следующем символическом виде:
Читателю может показаться непонятным, почему столь элементарная формула
где n — целое положительное число, носит имя великого ученого Ньютона, тем более что эта формула была известна до Ньютона. Например, ее знал Аль-Каши (XV век) и она встречается в трудах Паскаля. Объясняется это тем, что именно Ньютоном была обобщена эта формула для любого действительного показателя.
Ньютон впервые показал, что выражение
где 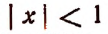
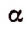
Например, если 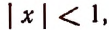
Видео:Бином Ньютона и его свойства. 9 класс.Скачать

Арифметический треугольник, или треугольник паскаля
Написанная ниже таблица
называется треугольником Паскаля *.
По боковым сторонам этой таблицы стоят единицы, внутри же стоят числа, получающиеся сложением двух соответствующих чисел предыдущей строки. Например, число 21 в 8-й строке получается сложением стоящих над ним чисел 6 и 15.
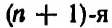
Треугольник Паскаля получается из следующей таблицы:
в силу того, что
Треугольник Паскаля приведен в книге Паскаля «Трактат об арифметическом треугольнике», изданной после его смерти в 1665 году.
Видео:Бином НьютонаСкачать

Примеры с решением на Бином Ньютона
1. В разложении 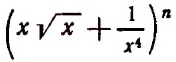
Решение:
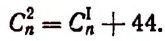
Приравняв показатель степени буквы х к нулю, получим:
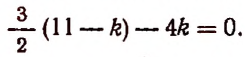
Искомым свободным членом будет четвертый, и он будет равен 
2. Сколько рациональных членов содержится в разложении
Решение:
Для рациональности члена разложения необходимо, чтобы число k было кратно четырем. Но тогда 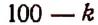
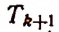
Число k может принимать целые значения 0, 1, 2….. 100. Среди этих чисел кратными четырем будут
Пользуясь формулой 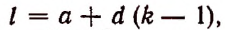

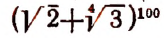
3. Доказать, что значение выражения
где n — натуральное число, делится на 9.
Доказательство:
Каждое слагаемое последней суммы делится на 9, следовательно, и вся эта сумма, т. е. значение выражения 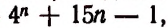
Видео:Математика для всех. Алексей Савватеев. Лекция 5.6. Бином НьютонаСкачать

Дополнение к Бином Ньютону
Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Видео:9 класс. алгебра. Решение уравнений.Скачать

Бином Ньютона
 Формула бинома Ньютона Формула бинома Ньютона |
 Связь бинома Ньютона с треугольником Паскаля Связь бинома Ньютона с треугольником Паскаля |
 Свойства биномиальных коэффициентов Свойства биномиальных коэффициентов |
Видео:Бином НьютонаСкачать

Формула бинома Ньютона
В Таблице 1 из раздела «Формулы сокращенного умножения» приведены формулы для натуральных степеней бинома
в случаях, когда n = 1, 2, 3, 4, 5, 6.
В настоящем разделе рассматривается общий случай этой формулы, т.е. случай произвольного натурального значения n .
Утверждение . Для любого натурального числа n и любых чисел x и y справедлива формула бинома Ньютона :
– числа сочетаний из n элементов по k элементов.
В формуле (1) слагаемые
называют членами разложения бинома Ньютона , а числа сочетаний 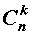
Если в формуле (1) заменить y на – y , то мы получим формулу для n — ой степени разности:
Видео:Уравнение 4-ой степени (x+3)^4+(x+5)^4=4Скачать

Связь бинома Ньютона с треугольником Паскаля
Напомним, что треугольник Паскаля имеет следующий вид:
| № | Треугольник Паскаля |
| 0 | 1 |
| 1 | 1 1 |
| 2 | 1 2 1 |
| 3 | 1 3 3 1 |
| 4 | 1 4 6 4 1 |
| 5 | 1 5 10 10 5 1 |
| 6 | 1 6 15 20 15 6 1 |
| … | … |
Поскольку числа, составляющие треугольник Паскаля, являются биномиальными коэффициентами, то треугольник Паскаля можно переписать в другом виде:
| № | Треугольник Паскаля |
| 0 | 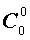 |
| 1 | 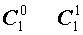 |
| 2 | 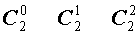 |
| 3 | 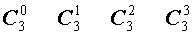 |
| 4 | 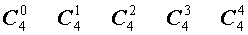 |
| 5 | 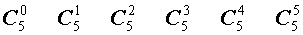 |
| 6 | 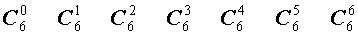 |
| … | … |
| Треугольник Паскаля |
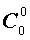 |
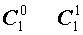 |
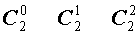 |
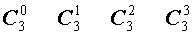 |
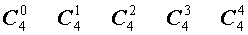 |
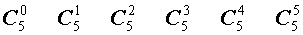 |
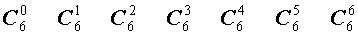 |
| … |
| Треугольник Паскаля |
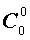 |
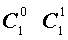 |
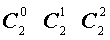 |
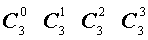 |
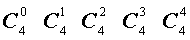 |
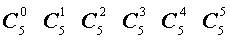 |
| … |
Видео:Уравнение четвертой степениСкачать

Свойства биномиальных коэффициентов
Для биномиальных коэффициентов справедливы равенства:
| 1 | 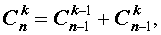 |
| 2 |