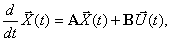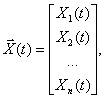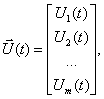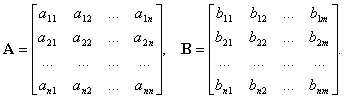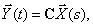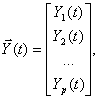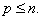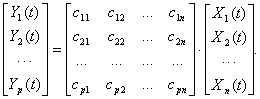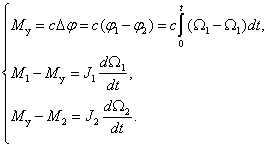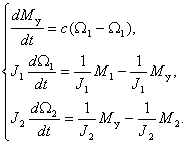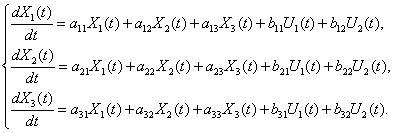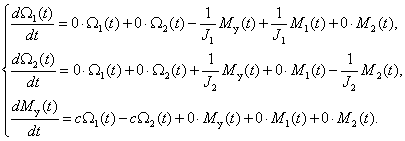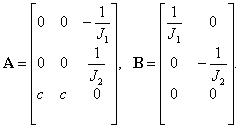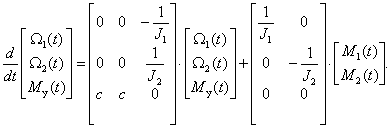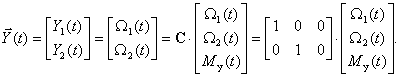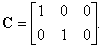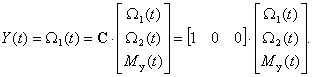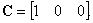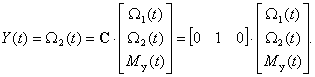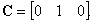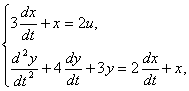Формирование уравнений состояния по дифференциальному уравнению (2 видео)

Уравнения состояния

При решении некоторых задач теории автоматического управления удобнее представлять дифференциальное уравнение объекта (5.1) или дифференциальные уравнения системы (5.4) и (5.6) в виде совокупности дифференциальных уравнений первого порядка. Не умаляя общности, рассмотрим эти уравнения применительно к управляемому объекту.

Пусть объект описывается дифференциальным уравнением n-го порядка (5.1)

называемых переменными состояния и представим уравнение (5.70) в виде системы дифференциальных уравнений

устанавливается алгебраическим уравнением

Обычно уравнения (5.71) и (5.72) записываются в векторпо-матричной форме:

— матрицы-столбцы. Матрицу-столбец-

могут иметь неодинаковые размерности.

В выборе переменных состояния имеется определенная свобода. Важно только, чтобы они были независимыми. От того, как выбраны переменные, зависит форма уравнений (5.73) и (5.74), т. е. вид входящих в них матриц.

При нормальной форме уравнений состояния в качестве переменных состояния выбираются сама управляемая величина п- 1 ее производные:

т. с. когда оно имеет вид

Достоинством нормальной формы является то, что переменные состояния имеют ясный физический смысл, а некоторые из них (например, хих2 и х:]) могут быть непосредственно измерены датчиками различных типов.

Для получения уравнений состояния в канонической форме уравнение объекта (5.70) представляется в виде

Если корни рь Ръ-Рп полинома С0(р) действительные однократные, то правая часть (5.80) может быть представлена в виде суммы элементарных дробей:

где К; и ()г- — коэффициенты разложения.

В качестве неременных состояния выбираются слагаемые суммы (5.81):

Большим достоинством канонической формы является диагоиальиость матрицы Л , что существенно упрощает решение уравнения (5.73). Основной недостаток ее состоит в том, что переменные состояния не имеют ясного физического смысла, в результате чего возникает проблема их непосредственного измерения.

Существуют и другие способы выбора переменных состояния, которые здесь не рассматриваются.

Решение векторно-матричиого уравнения (5.73) может быть представлено в виде

Здесь оно без строгого доказательства построено по аналогии с решением линейного дифференциального уравнения 1-го порядка

общий интеграл которого, как известно, определяется но формуле

называется переходной или фундаментальной матрицей. Если уравнения состояния представлены в канонической форме, то матрица А диагональная и имеет вид (5.85). Тогда

При других формах уравнений состояния для определения фундаментальной матрицы можно использовать известные способы нахождения матричных функций, например, теоремы Кели—Гамильтона или Сильвестра. Можно также использовать формулу

—

При необходимости можно осуществить обратный переход от уравнений состояния к передаточным функциям объекта. Для этого уравнение (5.73) запишем в изображениях по Лапласу:

получается формула (5.88). Из уравнения

(5.74) с учетом (5.89) найдем изображение управляемой величины при нулевых начальных значениях:

При описании свойств объекта уравнениями состояния возникают две проблемы, нетипичные для случая, когда используется одно дифференциальное уравнение я-то порядка. Эти проблемы рассматриваются в следующем параграфе.

Содержание

Формирование уравнений состояния по дифференциальному уравнению
Дифференциальные уравнения состояния
СОВРЕМЕННЫЕ СИСТЕМЫ УПРАВЛЕНИЯ
Требования к качеству системы в частотной области
Измерение частотных характеристик
Пример построения диаграммы Боде
Продажа шагающий экскаватор 20/90
📽️ Видео

Видео:11. Уравнения в полных дифференциалахСкачать

Формирование уравнений состояния по дифференциальному уравнению

Математические модели в пространстве состояний

Основу математической модели многомерной системы во временной области составляет векторно-матричная форма записи системы дифференциальных уравнений первого порядка, которая носит название уравнения состояния. Уравнение состояния имеет вид

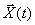
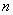
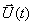
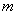
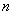
где вектор состояния размерности , который включает в себя переменные объекта, однозначно определяющие его состояние,

вектор управления или входа размерности , который включает в себя сигналы, действующие на систему извне,

матрицы параметров, включающие в себя параметры системы, размерность которых соответственно ,

порядок системы.

Иногда уравнение состояния (1) записывают в развернутой форме

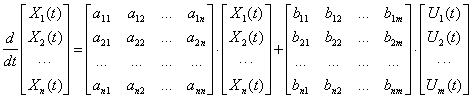
Уравнение состояния и структура полностью описывают объект управления, вектор состояния содержит переменные объекта, которые однозначно описывают его состояние.

Но в реальных системах многие компоненты не могут быть измерены или наблюдаемы с помощью датчиков. Эту ситуацию разрешает введение дополнительного уравнения выхода, которое определяет те переменные, которые доступны для наблюдения (на выходе системы)

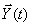
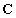
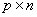
где вектор выхода размерности , который содержит переменные объекта, доступные для наблюдения,

матрица параметров размерности

в системах управления

Уравнение выхода (2) также можно записать в развернутой форме

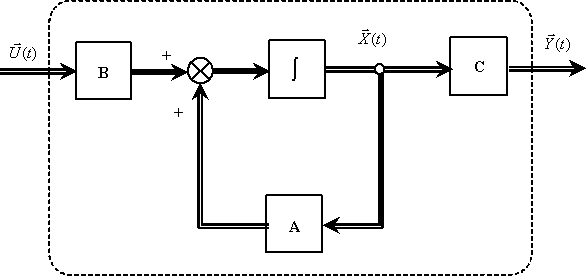
Графически уравнение состояния и уравнение выхода могут быть представлены в виде, показанном на рис. 1.

Символ интегрирования на схеме означает покомпонентное интегрирование векторной величины.

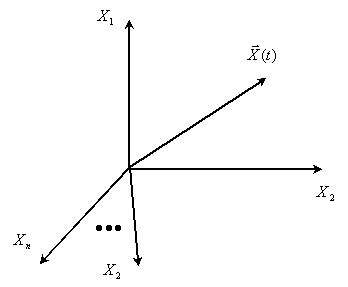
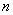
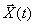
В общем виде пространство состояний мерной системы задается радиус-вектором в координатной системе, оси которой определяются компонентами вектора состояния, как это показано на рис. 2.

Рассмотрим несколько примеров представления процессов в пространстве состояний.

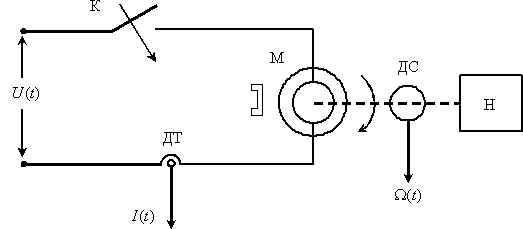
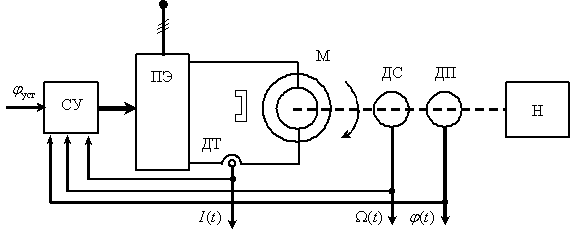
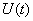
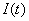
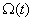
Рассмотрим в пространстве состояний процесс пуска электродвигателя (М) постоянного тока с постоянными магнитами, принципиальная схема установки показана на рис. 3. Пуск производится подключением с помощью контакта (К) напряжения , при этом в цепи будет протекать ток и двигатель будет вращать вал с нагрузкой (Н) со скоростью , ток и скорость определяются с помощью датчиков соответственно ДТ ДС.

Состояние двигателя в данном случае однозначно определяется током и скоростью двигателя, поэтому вектор состояния задаем в следующем виде

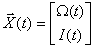
Вектор входа будет иметь только одну компоненту 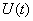. Графики изменения во времени переменных двигателя показаны на рис. 4.

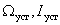
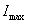
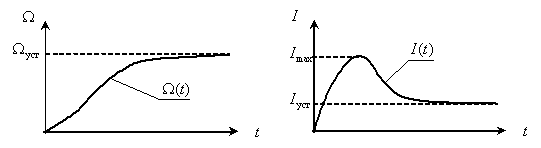
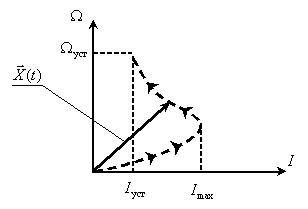
На рис. 4 введены обозначения: установившиеся значения соответственно скорости и тока, максимальное значение тока при пуске.

Сформируем двухмерное пространство состояний двигателя с траекторией движения конца вектора состояния в процессе пуска, для этого откладываем проекции вектора, то есть ток и скорость, в одинаковые моменты времени.

Рассмотрим в пространстве состояний процесс позиционирования, то есть перемещения вала в заданное положение 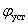, в автоматизированном электроприводе, показанном на рис. 6.

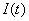
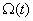
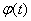
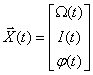
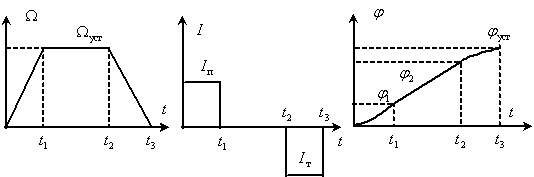
В этом случае состояние двигателя и всей системы электропривода в целом определяют три переменные двигателя ток , скорость и положение вала

Графики изменения во времени переменных двигателя показаны на рис. 7.

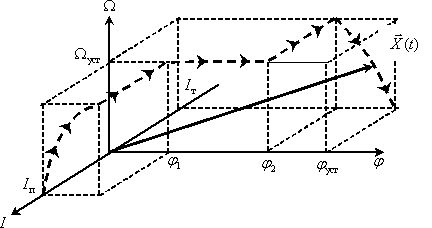
Сформируем трехмерное пространство состояний электропривода с траекторией движения конца вектора состояния в процессе позиционирования по временным графикам изменения компонент вектора состояния.

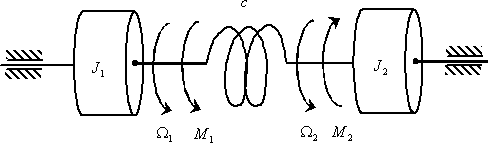
Теперь рассмотрим получения математической модели многомерного объекта в виде уравнений состояния на примере двухмассовой упругой механической системы, показанной на рис. 9.

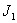
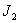
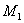
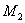
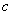
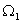
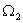
Двухмассовая упругая система представляет собой механическую систему, состоящую из двух вращающихся масс с моментами инерции и . К каждой массе прикладывается извне момент ( и ), массы соединены валом, обладающим упругими свойствами (), массы вращаются со скоростями и .

Система дифференциальных уравнений, описывающих систему, имеет вид

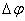
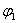
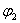
где разность углов положения первой и второй масс.

Так как уравнения состояния (1) и выхода (2) имеют единый для всех линейных систем вид, поэтому, чтобы определить их для конкретной системы мы должны выполнить следующее:

задать векторы состояния и входа, определив тем самым порядок системы и порядок вектора входа,

определить матрицы параметров уравнений.

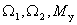
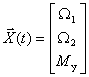
Состояние системы определяется тремя переменными , поэтому задаем вектор состояния следующего вида

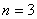
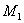
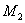
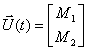
Порядок системы . Заметим, что положение переменных в векторе состояния можно задать произвольно, но в дальнейшем изменять его нельзя. Вектор входа определяется сигналами, действующими на систему извне, а это моменты и , поэтому вектор входа имеет вид

Порядок вектора выхода 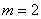. Здесь также порядок следования компонент может быть произвольным, но фиксированным в дальнейших операциях.

Преобразуем уравнения системы (3) к форме Коши

Нам требуется получить уравнение состояния для системы третьего порядка с вектором входа второго порядка, посмотрим, что представляет собой это уравнение в общем виде

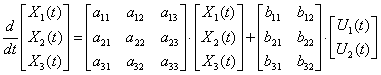
Раскрывая матричные скобки, получим

Теперь можно сформулировать задачу следующего этапа. Необходимо привести систему (4) в виду (5), для этого следует:

расположить уравнения в порядке следования компонент в векторе состояния,

расположить слагаемые в правых частях слева на право в порядке следования сначала компонент вектора состояния, затем вектора входа,

отсутствующие слагаемые заменяем произведениями переменных на нулевые коэффициенты.

В результате коэффициенты в правых частях при соответствующих компонентах векторов состояния и входа будут компонентами искомых матриц уравнения состояния.

Преобразуем систему (4) к виду (5), в результате получим

В результате по коэффициентам слагаемых в правых частях (6) получим искомые матрицы параметров уравнения состояния

Уравнение состояния в развернутом виде

Вид уравнения выхода определяется тем, какие компоненты вектора состояния доступны для наблюдения. В электромеханических системах электроприводов, эквивалентом которых является упругая двухмассовая система, возможны три варианты датчиковых систем (полагаем датчики безынерционными, а коэффициенты преобразования датчиков единичными):

Датчики скорости установлены на обеих массах. Тогда имеем следующее уравнение выхода

То есть имеем ,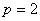

Датчик скорости установлен на первой массе, уравнение выхода

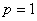
Датчик скорости установлен на второй массе, уравнение выхода

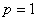
Контрольные вопросы и задачи

Перечислите компоненты уравнения состояния (векторы и матрицы), их размерности.

Поясните смысл уравнения выхода, перечислите компоненты и их размерности.

По системе дифференциальных уравнений, описывающих многомерную систему

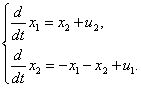
полагая векторы состояния и входа

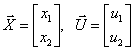
записать уравнение состояния в развернутой форме.

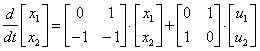
По уравнению состояния

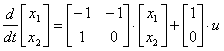
описывающему многомерную систему, определить систему дифференциальных уравнений, связывающих компоненты векторов состояния и входа.

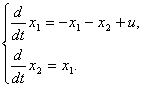
По системе дифференциальных уравнений, описывающих многомерную систему

полагая векторы состояния и входа

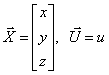
записать уравнение состояния в развернутой форме.

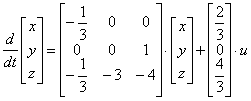
Видео:Дифференциальные уравнения. 11 класс.Скачать

Дифференциальные уравнения состояния

Состояние системы описывается дифференциальными уравнениями первого порядка относительно каждой из переменных состояния. Эти уравнения в общем случае имеют следующий вид:

X, = а2х + а22Х2 +■■■+ °2пхп + Ь7Щ +•••+ Ъ2:»»«». ^ щ

Хп — anjXj + ^/,7^2 +■■■+ аппхп ЬпЫ [2] Ь, п„и.

где x = dx/ dt. Эту же систему дифференциальных уравнений можно записать в матричной форме:

Матрица-столбец, состоящая из переменных состояния, называется вектором состояния

где полужирное начертание символа означает вектор. Вектор входных сигналов обозначается как и. Тогда систему можно описать в компактном виде дифференциальным уравнением состояния

Уравнение (3.16) часто называют просто уравнением состояния.

Матрица А является квадратной размерности пхп, а матрица В имеет размерность nxin. Уравнение состояния связывает скорость изменения состояния системы с самим состоянием и входными сигналами. В общем случае выходные сигналы линейной системы связаны с переменными состояния и входными сигналами уравнением выхода

где у —- совокупность выходных сигналов, представленная в виде вектора-столбца.

Воспользовавшись уравнениями (3.8) и (3.9), запишем уравнение состояния для ЛіС-цепи, изображенной на рис. 3.4:

Уравнение выхода будет иметь вид:

Если R — 3,L = и С = 1/2, то

Решение дифференциального уравнения состояния (3.16) можно получить точно так же, как решается скалярное дифференциальное уравнение первого порядка. Рассмотрим уравнение

где x(t) и и(/) — скалярные функции времени. Решение будем искать в виде экспоненты еа. Преобразуя уравнение (3.20) по Лапласу, получим:

sX(s) — — Х'(О) = aX(s) + bU(s),

Обратное преобразование Лапласа уравнения (3.21) дает искомое решение:

Аналогично получается и решение дифференциального уравнения состояния. Прежде всего введем в рассмотрение матричную экспоненциальную функцию, представив ее в виде ряда

еА’ = ехр( А/) = I + At +

который сходится для всех конечных t и любой А. Тогда решение уравнения состояния будет иметь вид:

Видео:18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать

СОВРЕМЕННЫЕ СИСТЕМЫ УПРАВЛЕНИЯ

Требования к качеству системы в частотной области

Мы постоянно должны задавать себе вопрос: какая связь существует между частотными характеристиками системы и ожидаемым видом её переходной характеристики? Другими словами, если задан набор требований к поведению системы во временной …

Измерение частотных характеристик

Синусоидальный сигнал можно использовать для измерения частотных характеристик разомкнутой системы управления. На практике это связано с получением графиков зависимости амплитуды и фазового сдвига выходного сигнала от частоты. Затем по этим …

Пример построения диаграммы Боде

Диаграмма Боде для передаточной функции G(s), содержащий несколько нулей и полюсов, строится путём суммирования частотных характеристик, соответствующих каждому отдельно взятому полюсу и нулю. Простоту и удобство данного метода мы проиллюстрируем …

Видео:Откуда появляются дифференциальные уравнения и как их решатьСкачать

Продажа шагающий экскаватор 20/90

Цена договорная
Используются в горнодобывающей промышленности при добыче полезных ископаемых (уголь, сланцы, руды черных и
цветных металлов, золото, сырье для химической промышленности, огнеупоров и др.) открытым способом. Их назначение – вскрышные работы с укладкой породы в выработанное пространство или на борт карьера. Экскаваторы способны
перемещать горную массу на большие расстояния. При разработке пород повышенной прочности требуется частичное или
сплошное рыхление взрыванием.
Вместимость ковша, м3 20
Длина стрелы, м 90
Угол наклона стрелы, град 32
Концевая нагрузка (max.) тс 63
Продолжительность рабочего цикла (грунт первой категории), с 60
Высота выгрузки, м 38,5
Глубина копания, м 42,5
Радиус выгрузки, м 83
Просвет под задней частью платформы, м 1,61
Диаметр опорной базы, м 14,5
Удельное давление на грунт при работе и передвижении, МПа 0,105/0,24
Размеры башмака (длина и ширина), м 13 х 2,5
Рабочая масса, т 1690
Мощность механизма подъема, кВт 2х1120
Мощность механизма поворота, кВт 4х250
Мощность механизма тяги, кВт 2х1120
Мощность механизма хода, кВт 2х400
Мощность сетевого двигателя, кВ 2х1600
Напряжение питающей сети, кВ 6
Более детальную информацию можете получить по телефону (063)0416788