- Гидростатика и ее законы
- Гидростатическое давление
- Основное уравнение гидростатики. Закон Паскаля.
- Пример решения задачи с использованием закона Паскаля
- Вопрос №21. Как формулируется закон Паскаля и какова его связь с основным уравнением гидростатики?
- Элементы гидростатики
- Закон Паскаля
- Закон Архимеда
- Закон Паскаля для газов и жидкостей в гидростатике
- Закон Паскаля для жидкости и газа
- Закон Паскаля в гидростатике описание
- Вывод формулы закона Паскаля в гидростатике
- 🎦 Видео
Видео:Гидростатическое давлениеСкачать

Гидростатика и ее законы
Гидростатика – раздел гидравлики, в котором изучаются законы равновесия жидкостей, находящихся в покое.
Понятие покоя или равновесного состояния по отношению к жидкости можно отождествлять с аналогичным понятием в одном из разделов технической механики — статике. Любое тело, материальная точка или обособленный объем вещества (в т. ч. жидкости) считается покоящимся, если все силы (внешние и реактивные), действующие на этот материально существующий субъект (т. е. имеющий массу), уравновешивают друг друга.
Тем не менее, жидкость по своим свойствам и «способностям» уникальна, поэтому гидростатика призвана пояснить некоторые особенности поведения жидкого вещества в тех или иных условиях.
Гидростатическое давление
На жидкость, находящуюся в покое действуют массовые и поверхностные силы. Массовыми являются силы, действующие на все частицы рассматриваемого объема жидкости. Это силы тяжести и силы инерции (силы инерции проявляются в движущейся жидкости, поэтому их учитывает раздел гидродинамика) .
Массовые силы пропорциональны массе жидкости, а для однородной жидкости, плотность которой одинакова во всех точках, — объему. Поэтому массовые силы называют еще объемными.
К поверхностным относятся силы, действующие на поверхности жидкости. Это, например, атмосферное давление, действующее на жидкость в открытом сосуде, или силы трения, возникающие в движущейся жидкости между отдельными слоями и стенками сосуда (в покоящейся жидкости силы трения отсутствуют) .
Жидкость, находящаяся в состоянии покоя, может находиться только под действием силы тяжести и поверхностных сил, вызванных внешним давлением (например, атмосферным) . Внешние силы давления являются нормальными сжимающими поверхностными силами (считается, что жидкость не сопротивляется растяжению) . Все эти силы создают в неподвижной жидкости некоторую равнодействующую (результирующую) силу, которая называется гидростатической силой .
Покоящаяся жидкость под воздействием гидростатической силы находится в напряженном состоянии, характеризуемом гидростатическим давлением.
Выделим в покоящейся жидкости произвольный объем (см. рис. 1) . Мысленно разделим этот объем произвольной плоскостью П . Выделим на полученном сечении точку А и некоторую площадку ΔS вокруг этой точки.

Отношение гидростатической силы к площади поверхности (выделенного сечения) жидкости называют средним гидростатическим давлением. Истинное гидростатическое давление в данной точке жидкости может быть определено, как предел, к которому стремится среднее гидростатическое давление при бесконечном уменьшении рассматриваемой площадки ΔS :
p = lim ΔP/ΔS при ΔS стремящемся к нулю.
Гидростатическое давление всегда направлено по внутренней нормали к площадке, на которую оно действует, и величина его в произвольной точке не зависит от ориентации этой площадки в пространстве.
Это утверждение вытекает из условий:
— неподвижности жидкости, поскольку при любом перемещении жидкости неизбежно возникают касательные напряжения;
— равновесия рассматриваемого элементарного (бесконечно малого) объема, поскольку равновесие может быть достигнуто лишь при равенстве всех действующих на рассматриваемый элементарный объем внешних сил (предполагается, что весом бесконечно малого объема жидкости можно пренебречь) .
При этом выделенный объем может иметь любую произвольную форму – куба, правильной пирамиды и т. д. – в любом случае легко доказать, что силы, действующие на грани этого объема будут одинаковы во всех направлениях.
Основное уравнение гидростатики. Закон Паскаля.
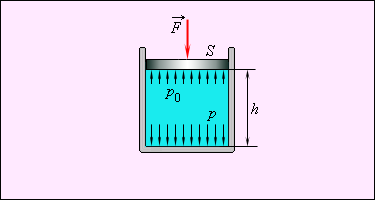
Выделим в однородной жидкости, находящейся в покое, элементарный объем ΔV в виде прямоугольного параллелепипеда с площадью горизонтального основания ΔS и высотой H (см. рис. 2) .
Рассмотри условия равновесия выделенного элементарного объема.
Пусть давление на плоскость верхнего основания равно р1 , а на плоскость нижнего основания – р .
Силы давления действующие на вертикальные грани выделенного параллелепипеда взаимно уравновешиваются как равные по величине и противоположно направленные.
На горизонтальные грани действуют силы давления, направленные вертикально: на верхнюю грань эта сила будет равна р1ΔS (направлена вниз) , на нижнюю – pΔS (направлена вверх) .
На верхнюю и нижнюю грани рассматриваемого параллелепипеда действуют силы, обусловленные давлением на жидкость со стороны внешней среды (например, атмосферного давления) и вес (сила тяжести) элементарного столбика жидкости над каждой из горизонтальных граней параллелепипеда.
Очевидно, что разность сил тяжести, действующих на верхнюю и нижнюю площадку, будет равна весу жидкости, заключенной в объеме рассматриваемого параллелепипеда, который равен ρgΔV ,
где ρ – плотность жидкости, g – ускорение свободного падения, ΔV – объем параллелепипеда: ΔV = HΔS .
Исходя из условия равновесия выделенного элементарного параллелепипеда объемом ΔV , можно утверждать, что сумма всех внешних сил, действующих на параллелепипед равна нулю, т. е.:
pΔS – p1ΔS – ρgΔV = pΔS – p1ΔS – ρgΔSH = 0 .
Преобразовав эту формулу, получим величину гидростатического давления на нижнюю горизонтальную площадку:
Если верхняя грань параллелепипеда граничит с внешней средой (например, атмосферой) , оказывающей давление р0 на жидкость, то формула может быть переписана в виде:
Это выражение является основным уравнением гидростатики .
Итак, гидростатическое давление в любой точке внутри покоящейся жидкости равно сумме давления на свободную поверхность со стороны внешней среды и давления столба жидкости высотой, равной глубине погружения точки (т. е. ее расстоянию от свободной поверхности жидкости) .
На основании основного уравнения гидростатики может быть сформулирован закон Паскаля: внешнее давление, производимое на свободную поверхность покоящейся жидкости, передается одинаково всем ее точкам по всем направлениям.
Блез Паскаль (Blaise Pascal, 1623 — 1662) — выдающийся французский ученый — математик, механик, физик, литератор и философ. Классик французской литературы, один из основателей математического анализа, теории вероятностей и проективной геометрии, создатель первых образцов счётной техники, автор основного закона гидростатики.
Любопытны цитаты из популярного сборника высказываний Паскаля, не потерявшие актуальность и в наши дни.
Вот некоторые из них:
- Искание истины совершается не с весельем, а с волнением и беспокойством; но все таки надо искать ее потому, что, не найдя истины и не полюбив ее, ты погибнешь.
- Прошлое и настоящее — наши средства, только будущее — наша цель.
- Нас утешает любой пустяк, потому что любой пустяк приводит нас в уныние.
- Когда человек пытается довести свои добродетели до крайних пределов, его начинают обступать пороки.
- Справедливость должна быть сильной, а сила должна быть справедливой.
- Истина так нежна, что чуть только отступил от нее, впадаешь в заблуждение, но и заблуждение это так тонко, что стоит только немного отклониться от него, и оказываешься в истине.
- Величие не в том, чтобы впадать в крайность, но в том, чтобы касаться одновременно двух крайностей и заполнять промежуток между ними.
- Изучая истину, можно иметь троякую цель: открыть истину, когда ищем ее; доказать ее, когда нашли; наконец, отличить от лжи, когда ее рассматриваем.
- Сила добродетели человека должна измеряться не его усилиями, а его повседневной жизнью.
- Лишь в конце работы мы обычно узнаём, с чего нужно было её начать.
- Существует достаточно света для тех, кто хочет видеть, и достаточно мрака для тех, кто не хочет.
- Человек — это приговорённый к смерти, казнь которого откладывается на время его жизни.
Умер Паскаль после тяжелой и продолжительной болезни в возрасте 39 лет, оставив после себя яркий след в науке.
Имя этого ученого увековечено в названиях одной из единиц международной системы СИ, языка программирования Paskal и лунного кратера.
Пример решения задачи с использованием закона Паскаля
Водолазы при подъеме затонувшего судна работали на глубине 50 м. Определить давление p воды на этой глубине и силу P давления на скафандр водолаза, если площадь его поверхности S равна 1 м 2 .
Атмосферное давление считать равным 1013 МПа (0,1013×106 Па), плотность воды – 1000 кг/м 3 .
Решение:
Определим давление, оказываемое столбом воды на глубине 50 м (в Па) :
ρgH = 1000×9,81×50 = 4,9×105 Па.
Применив основное уравнение гидростатики, с учетом атмосферного давления, найдем давление на глубине 50 м:
p = p0 + ρgH = 1,013×105 + 4,9×105 = 5,91×105 Па ≈ 0,59 МПа.
Силу давления столба воды на скафандр водолаза определим по формуле:
P = pS = 5,91×105×1 = 591000 Н = 591 кН.
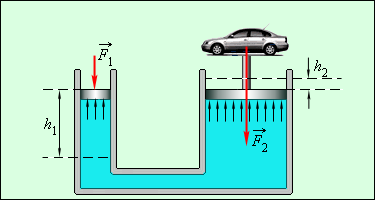
Основное уравнение гидростатики и закон Паскаля широко применяются при решении многих инженерных задач. Свойства жидкости передавать производимое на нее давление без изменения используется при конструировании гидравлических прессов, домкратов, гидроаккумуляторов, гидроприводов и других механизмов. Основной принцип работы этих устройств основа на пропорциональной разности сил, приложенных к поршням гидроцилиндров, имеющих разный диаметр: P1S2 = P2S1 .
Видео:Закон ПаскаляСкачать

Вопрос №21. Как формулируется закон Паскаля и какова его связь с основным уравнением гидростатики?
Читайте также:
|


 .
. .
.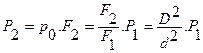 . (2 – 6)
. (2 – 6)