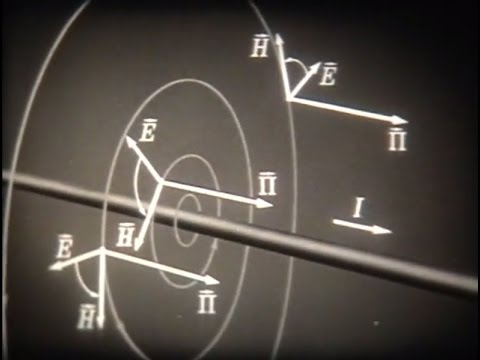
Все электромагнитные процессы макроскопической электродинамики подчиняются уравнениям Максвелла, сформулированным в 1873 г. в виде дифференциальных уравнений. Эти уравнения связывают воедино электрические и магнитные характеристики поля:
rot H = Iпр + 

rot Е = — 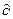

div D = 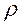
Физический смысл этих уравнений заключается в следующем.
Первое уравнение Максвелла(5.9,а) является обобщенным законом Ампера (закон полного тока) и говорит о том, что если в некоторой точке пространства существует переменное электрическое поле Е, создающее токи проводимости Iпр = σE и токи смещения Iсм = iω 
Второе уравнение Максвелла (5.9,б) является обобщенным законом магнитной индукции Фарадея. Фарадей установил, что если замкнутый контур пронизывается переменным магнитным потоком Ф, то в контуре возникает электродвижущая сила (ЭДС) равная скорости изменения магнитного потока:
е = — 

Знак «минус» в правой части означает, что возникающая в контуре ЭДС стремится воспрепятствовать изменению потока, пронизывающего контур.
Физический смысл второго уравнения Максвелла заключается в том, что всякое изменение магнитного поля во времени непрерывно вызывает независимо от параметров среды появление электрического поля.
Второе уравнение Максвелла связано с гармоническим колебанием соотношением:
rot Е = — 

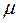
т.е. оно утверждает, что если в некоторой точке пространства существует переменное магнитное поле, то в окрестностях этой точки возникает переменное вихревое электрическое поле. Магнитное поле и создаваемое им электрическое поле образуют левовинтовую систему.
Следует отметить, что электрическое поле может быть как вихревым, так и потенциальным. Источником потенциального электрического поля являются заряды (в случае электрических полей), которые находятся в тех точках пространства, где текут токи проводимости, представляющие собой движущиеся заряды.
Таким образом, гармоническое электрическое поле может быть вихревым, потенциальным или представлять суперпозицию (сумму) потенциального и вихревого полей, тогда как магнитное поле только вихревое.
Первое и второе уравнения Максвелла говорят о том, что между электрической и магнитной составляющими в переменном электромагнитном поле существует тесная взаимосвязь, которая выражается тем, что созданное сторонними источниками меняющееся во времени электромагнитное поле, может существовать вне этого источника за счет собственной энергии, перекачивающейся из энергии электрического поля в энергию магнитного поля и обратно.
Третье уравнение Максвелла(материальное уравнение 5.9,в) — это обобщенный закон Гаусса для случая переменных процессов, физически означает, что источником электрического поля являются электрические заряды, т.е. электрическая индукция D связана с плотностью электрических зарядов 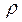
Четвертое уравнениеМаксвелла (материальное уравнение 5.9,г) показывает, что в природе отсутствуют магнитные заряды, а линии вектора В непрерывны и всегда пронизывают любую замкнутую поверхность.
Таким образом, третье и четвертое уравнения Максвелла учитывают электрическую и магнитную характеристики среды. Действительно, в случае линейных изотропных сред можно записать:
D = 
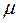
Следует отметить, что к основным уравнениям электродинамики относят и закон Ома в дифференциальной форме (5.6), который выражает зависимость плотности тока Iпр в какой-либо точке проводящей сферы от напряженности электрического поля в этой точке.
Таким образом, мы рассмотрели основные уравнения электродинамики, каждое из которых описывает те или иные свойства электромагнитного поля. Однако, для полного анализа электродинамических процессов необходимо использовать полную систему уравнений Максвелла, содержащую основные уравнения Максвелла (5.9,а-г) и материальные уравнения (5.6) и (5.10), которая записывается в виде:
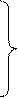



rot Е = — 

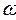
div D = 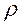
D = 
Поскольку уравнения (5.13) и (5.14) являются линейными дифференциальными уравнениями, можно утверждать, что электромагнитные поля удовлетворяют принципу суперпозиции.
Видео:Билеты №32, 33 "Уравнения Максвелла"Скачать

Тема: Уравнения Максвелла
Тема: Уравнения Максвелла
Физический смысл уравнения Максвелла 
источником электрического поля являются свободные электрические заряды
Решение:
Данное уравнение Максвелла является обобщением теоремы Остроградского – Гаусса для электростатического поля в среде – источником электрического поля являются свободные электрические заряды. Максвелл предположил, что она справедлива для любого электрического поля, как стационарного, так и переменного.
Тема: Уравнения Максвелла
Утверждение «Переменное электрическое поле, наряду с электрическим током, является источником магнитного поля» раскрывает физический смысл уравнения …
Тема: Уравнения Максвелла
Физический смысл уравнения Максвелла 
источником электрического поля являются свободные электрические заряды
изменяющееся со временем магнитное поле порождает вихревое электрическое поле
«магнитных зарядов» не существует: силовые линии магнитного поля замкнуты
источником вихревого магнитного поля, помимо токов проводимости, является изменяющееся со временем электрическое поле
Решение:
Данное уравнение Максвелла является обобщением теоремы Остроградского – Гаусса для электростатического поля в среде – источником электрического поля являются свободные электрические заряды. Максвелл предположил, что она справедлива для любого электрического поля, как стационарного, так и переменного.
Тема: Уравнения Максвелла
Физический смысл уравнения Максвелла 
источником электрического поля являются свободные электрические заряды
Решение:
Данное уравнение Максвелла является обобщением теоремы Остроградского – Гаусса для электростатического поля в среде – источником электрического поля являются свободные электрические заряды. Максвелл предположил, что она справедлива для любого электрического поля, как стационарного, так и переменного.
Тема: Уравнения Максвелла
Физический смысл уравнения Максвелла 
источником электрического поля являются свободные электрические заряды
Тема: Уравнения Максвелла
Физический смысл уравнения Максвелла 
источником электрического поля являются свободные электрические заряды
Тема: Уравнения Максвелла
Обобщением теоремы Остроградского – Гаусса для электростатического поля в среде является уравнение …
Решение:
Уравнение Максвелла 
Тема: Уравнения Максвелла
Физический смысл уравнения Максвелла 
источником вихревого магнитного поля помимо токов проводимости является изменяющееся со временем электрическое поле
Тема: Уравнения Максвелла
Физический смысл уравнения Максвелла 
«магнитных зарядов» не существует: силовые линии магнитного поля замкнуты
Решение:
Уравнение Максвелла 
Тема: Уравнения Максвелла
Утверждение «Переменное электрическое поле, наряду с электрическим током, является источником магнитного поля» раскрывает физический смысл уравнения …
Решение:
Из уравнения 

Тема: Уравнения Максвелла
Полная система уравнений Максвелла для электромагнитного поля в интегральной форме имеет вид:



Следующая система уравнений:



справедлива для …
электромагнитного поля в отсутствие свободных зарядов
Решение:
Вторая система уравнений отличается от первой системы своими вторым и третьим уравнениями. Во втором уравнении иначе записано подынтегральное выражение, но 

Тема: Уравнения Максвелла
Уравнения Максвелла являются основными законами классической макроскопической электродинамики, сформулированными на основе обобщения важнейших законов электростатики и электромагнетизма. Эти уравнения в интегральной форме имеют вид:
1).
2).
3).
4). 
Третье уравнение Максвелла является обобщением …
теоремы Остроградского – Гаусса для электростатического поля в среде
Решение:
Третье уравнение Максвелла является обобщением теоремы Остроградского – Гаусса для электростатического поля в среде. Максвелл предположил, что она справедлива для любого электрического поля, как стационарного, так и переменного.
Тема: Уравнения Максвелла
Физический смысл уравнения Максвелла 
источником электрического поля являются свободные электрические заряды
Тема: Уравнения Максвелла
Физический смысл уравнения Максвелла 
источником вихревого магнитного поля помимо токов проводимости является изменяющееся со временем электрическое поле
Тема: Уравнения Максвелла
Полная система уравнений Максвелла для электромагнитного поля в интегральной форме имеет вид:



Следующая система уравнений:



справедлива для …
электромагнитного поля при наличии заряженных тел и в отсутствие токов проводимости
Тема: Уравнения Максвелла
Утверждение «Переменное электрическое поле, наряду с электрическим током, является источником магнитного поля» раскрывает физический смысл уравнения …
Решение:
Из уравнения 

Видео:ЧК_МИФ: 4.1.1.ДФ_1 Физический смысл уравнений МаксвеллаСкачать

Уравнения Максвелла — формулы и физический смысл
Взаимодействие между электрическими зарядами, обладающими дипольным моментом, характеризуется возникновением электромагнитного поля. Изучает это явление электродинамика. Фундаментальными правилами в этом разделе физики являются уравнения Максвелла. С их помощью можно определить поля, учитывая распределение зарядов и токов. Существует четыре закона, в своё время совершившие переворот в научном мире.
Видео:О чем говорят уравнения Максвелла? Видео 1/2Скачать

Основная идея
Если в замкнутом контуре меняется магнитный поток, то по нему течёт электрический ток. В итоге возникает электродвижущая сила магнитной индукции. Происходит это из-за изменения магнитного поля. Предположим, имеется магнит, у которого поток с течением времени увеличивается. Если в поле поместить замкнутый проводник кольцевого типа, то по правилу Ленца в нём возникнет индукционный ток, противоположный магнитной силе через контур.
Ток — это направленное движение заряженных частиц. Сила, заставляющая их перемещаться, называется электрическим полем. Появляется она при изменении магнитного потока. Отсюда можно сделать вывод, что электрическое поле существует всегда там, где есть изменяющееся магнитное, при этом оно имеет замкнутую форму. Этот вид силы и называли вихревым полем. Когда вектор магнитной силы возрастает, то увеличивается и вихревое поле, а если убывает, то, соответственно, оно уменьшается.
Джеймс Клерк Максвелл предположил, что если меняющееся магнитное поле порождает электрическое, то этот процесс может быть и обратным. Его идея заключалась в том, что если имеется проводник с током, то вокруг него существует стационарное магнитное поле. На длине этого проводника он выбрал произвольные три точки равноудалённые от него на расстояние r.
В этих точках поле будет одинаковое. Максвелл предположил, что если проводник разорвать, то для того чтобы ток продолжал движение, нужно сохранить заряды. То есть фактически использовать конденсатор. По мнению Максвелла, тогда в точке разрыва поле будет такое же, как и вокруг проводника. Между обкладками возникнет электрическая сила, так как на них происходит сохранение (накопление) зарядов. Учитывая это, физик пришёл к выводу, что изменяющееся электрическое поле приводит к возникновению магнитного потока.
Так как на обкладках имеется заряд, то сила тока будет равняться I = dq / dt. Заряд можно связать с напряжением на обкладках конденсатора и электроёмкостью: q = C * U. Ёмкость же в вакууме определяется как E0 * S/ d, а напряжение — как E * d.
Подставив значения в формулу, Максвелл получил выражение: dq / dt = E0 * S * dE / dt. Так как ток между обкладками не течёт, а перенос происходит полем, физик предложил ввести понятие фиктивный ток смещения. Плотность этого тока можно найти по формуле: j = E0 * dE / dt. Это позволило упростить вычисления магнитной силы. Ток смещения и вихревое поле стали основой для создания системы уравнений.
Видео:Уравнения Максвелла и соответствующие уравнения Волновой МоделиСкачать

Физическая суть
Электромагнитное поле представляет собой материю, с помощью которой заряженные элементарные частицы взаимодействуют между собой. В вакууме явление характеризуется напряжённостью E и магнитной индукцией B. Эти параметры определяют силы, воздействующие на подвижные и неподвижные заряды. Кроме них, значение электромагнитного поля определяется скалярным и векторным потенциалами и двумя дополнительными величинами: индукцией D и напряжённостью магнитных линий H.
Открытие в 1831 году Фарадеем закона электромагнитной индукции, устанавливающего зависимость между зарядом и намагниченностью у токоведущих тел, помогло Максвеллу сформулировать ряд уравнений, после названных его именем. Главное его исследование заключалось в исследовании тока смещения, равного по магнитному действию электрическому току.
Сформулировав свою систему, физик смог связать электрическое и магнитное поле с зарядом и током. Физический смысл уравнений Максвелла заключается в том, что электромагнитное поле рассматривалось им как самостоятельный объект, в котором передача энергии происходит колебанием от точки к точке с конечной скоростью. При этом в вакууме она определяется скоростью света.
С точки зрения математики, для описания процессов учёный использовал векторный анализ, выраженный через инвариантную форму, использующую кватернионы Гамильтона. Написанные им уравнения неохотно принимались учёным советом Лондонского Королевского общества. Это происходило из-за того, что они не были похожи ни на одно из описаний известных ранее.
Тем не менее система Максвелла получила признание и стала фундаментальной в области электродинамики. При этом её справедливость получила подтверждение не только в микромире, ни и в области квантовой физики.
Основным следствием открытия стало понятие о скорости распространения электромагнитных волн и создании теории света. По сути, эта система теории волн в науке об электромагнетизме играет роль сопоставимую с законами Ньютона в области механики или с теоремами в электродинамике.
Видео:Физика. Лекция 8. Уравнения Максвелла и электромагнитные волны.Скачать

Дифференциальная запись
Открытие в проводящих телах тока смещения позволило Максвеллу вывести четыре уравнения, на основе которых была создана теория электромагнитных явлений. Обычно в физике математическая запись процессов не зависит от системы единиц, но в термодинамике это не так. Всё дело в том, что при записи в различных системах изменяются коэффициенты (постоянные).
Например, в системе единиц, используемой в описании квантовой теории поля, скорость света и электромагнитная константа равна единице. Поэтому уравнения не будут иметь ни одной постоянной. Для записи используют две системы: СГС — симметричная гауссова, и СИ — Международная система единиц.
В этих двух стандартах система уравнений Максвелла может быть описана словесно и математически следующим образом:
Это классические четыре закона описывающие природу и условия возникновения электромагнитного поля. Первая гипотеза связывает напряжённость с индукцией и является выражением теоремы электромагнитной индукции. Вторая доказывает отсутствие объектов, генерирующих магнитное поле. Третья устанавливает зависимость между током смещения и проводимостью, создающейся в магнитном поле. Четвёртая объясняет, что источником вектора электрической индукции служит сторонний заряд.
Указанные уравнения представляют собой запись в дифференциальной форме. При этом каждое из них эквивалентно скалярным уравнениям. В этой форме они имеют следующий вид:
Для того чтобы воспользоваться этими постулатами для расчёта полей, нужно уравнения дополнить граничными правилами объединяющим электрическую индукцию (D), плотность электрического тока (j), напряжённость (E). Эти положения имеют вид: D = e0*e*E; B = m0*m*H; j = δ*E. Совокупность этих соотношений позволяет сделать вывод об основе электродинамики сред, находящихся в спокойном состоянии.
Видео:3 14 Уравнения МаксвеллаСкачать

Интегральная форма
Запись уравнений Максвелла в интегральной и дифференциальной форме позволяет рассчитать электромагнитное поле в любой среде. Первые два уравнения, включающие интегралы, получаются путём преобразования дифференциальных форм по произвольной поверхности и применения теоремы Стокса, ограничивающей поверхность. Вторые же два путём интегрирования по произвольному объёму с дальнейшим их упрощением по теореме Остроградского — Гаусса, по ограниченной поверхности в замкнутом объёме.
Выглядят они следующим образом:
В этих уравнениях буквой S обозначается замкнутое пространство двухмерной поверхности определяющей границы объёма V или контура l. При этом Q является электрическим зарядом, находящимся в замкнутом объёме площадью S и равным: Q = ∫p * dV, а I — электрическим током, протекающим сквозь S и определяющимся из уравнения: I = ∫j * ds.
Нужно отметить, что вектор потока по ограниченной поверхности считается направленным из объёма. Вращение же находится согласно правилу правого винта по незамкнутой площади. В уравнениях величины E, B, D и H являются равнозначными значениями, определяющимися в результате решения системы.
Видео:Уравнения Максвелла 2021Скачать

Значение уравнений
Система уравнений Максвелла для электромагнитного поля объясняет все электромагнитные явления. Её применяют при полном анализе полей при известных распределениях токов и заряженных частиц. Часто уравнения называют материальными, подчёркивая индивидуальные свойства занимающей пространство среды: D = e * e0 * E, B = m * m0 * H, J = E .
Формулы физика подтверждают существование электромагнитных волн. Иначе говоря, предпологают возможность электрического поля излучать энергию вне зависимости от присутствия электрических зарядов и токов. Из всего многообразия применения уравнений можно выделить основные четыре:
Система включает в себя все основные законы электрического и магнитного поля с учётом такого важного параметра, как электромагнитная индукция. Теоретическое исследование физика позволило утверждать, что свет представляет собой электромагнитные волны и существования токов смещения в магнитном поле. То есть изменение ЭМП без движения электрических зарядов. Благодаря этому стало возможным находить полный ток.
Максвеллом было найдено четыре важных закономерности, заключающиеся в том, что электрический заряд образует электрическое поле, колебания магнитных волн порождает электрические вихри, магнитных зарядов быть не может, изменение индукции приводит к появлению вихревого магнитного потока. Эти теоретические суждения после были подтверждены экспериментально и позволили получить картину распространения свободной энергии электромагнитной волны в пространстве.
🎦 Видео
Лекция №9. Уравнения МаксвеллаСкачать

Джеймс Клерк Максвелл. Научные труды и вклад в наукуСкачать

Урок 383. Вихревое электрическое поле. Ток смещенияСкачать

Электромагнитные волны и уравнения Максвелла — Эмиль АхмедовСкачать

Вывод уравнений МаксвеллаСкачать

Физические ошибки. Уравнения МаксвеллаСкачать

Теория поля 6. Вторая пара уравнений Максвелла. Законы сохранения ЭМ поля.Скачать

Лекция №19 "Уравнения Максвелла"Скачать

Электродинамика | уравнения Максвелла | 1 | для взрослыхСкачать
Уравнения Максвелла — Мартин МакколлСкачать

Лекция №14 "Электричество и магнетизм" (Попов П.В.): Уравнения МаксвеллаСкачать

Основные физические понятия технической электродинамики, 1978Скачать