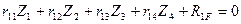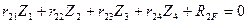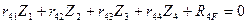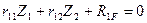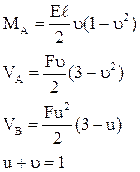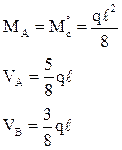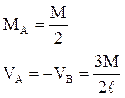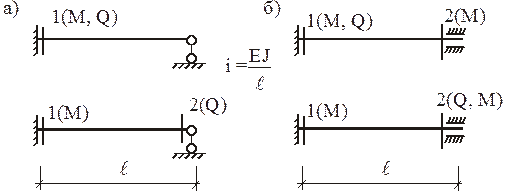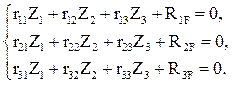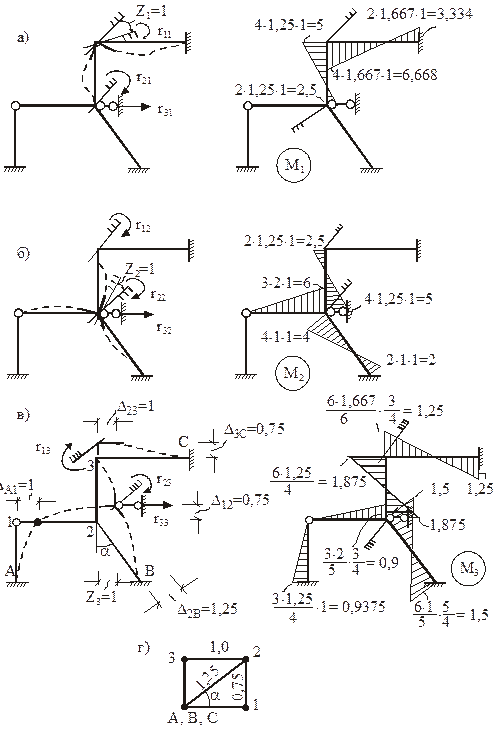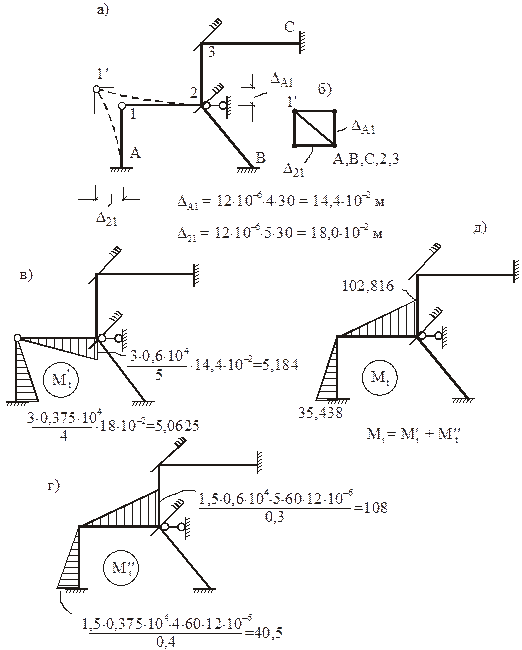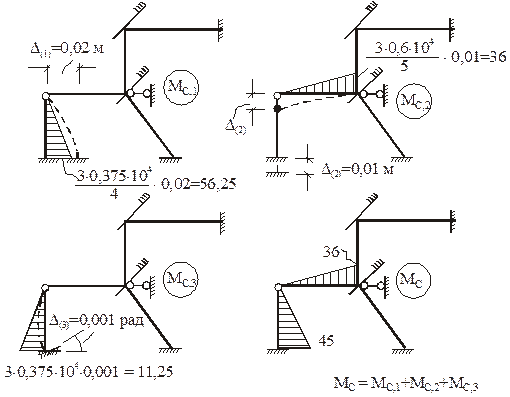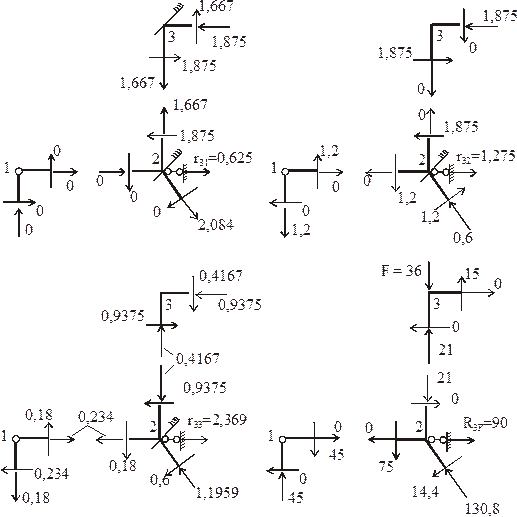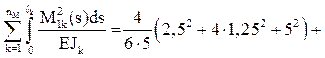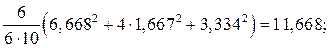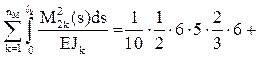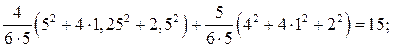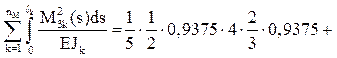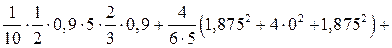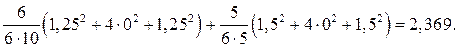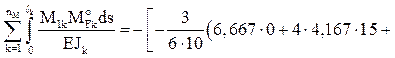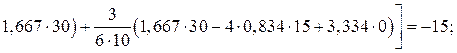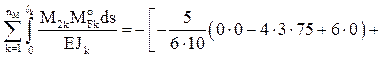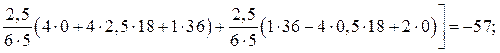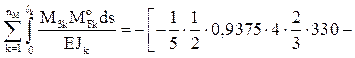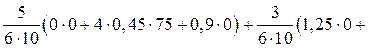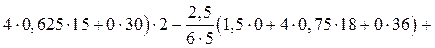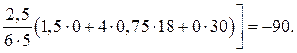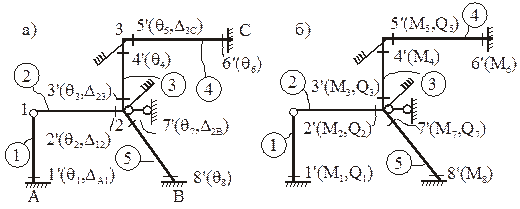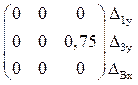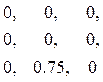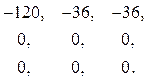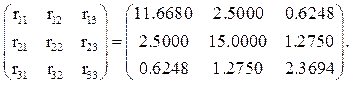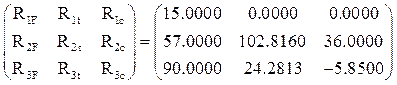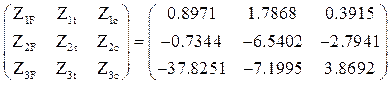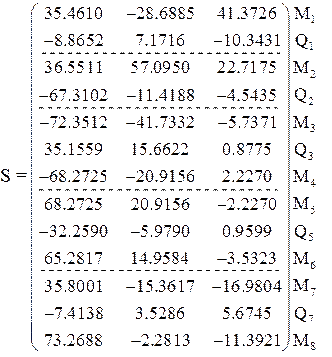Канонические уравнения метода перемещений
В каждой условно введенной связи основной системы возникают реактивные усилия как от действия внешней нагрузки, так и от смещения связей. В заделках возникают реактивные моменты, а в линейных связях — реактивные усилия.
Условия эквивалентности заданной и основной систем в методе перемещений записывают в виде системы канонических уравнений
Канонические уравнения метода перемещений (8.4) описывают реактивные усилия в условных связях и заделках основной системы как от перемещений этих связей и заделок, так и от заданной внешней нагрузки.
Физический смысл коэффициентов при неизвестных перемещениях Zi заключается в том, что rij представляет собой реактивное усилие в i-й условной заделке или связи в основной системе от перемещения j-й условной заделки или связи на единицу.
Физический смысл свободного члена RiF системы канонических уравнений метода перемещений заключается в том, что он представляет собой реактивное усилие в i-й условной связи или заделке от внешней нагрузки.
Равенство нулю каждого из уравнений означает, что в заданной системе нет ни заделок, ни связей, т.к. они являются условными.
Система канонических уравнений метода перемещений в матричной форме имеет следующий вид:
где — матрица реакций; — вектор реакций от внешней нагрузки; — вектор искомых перемещений.
В матрице реакций различают «главные» реакции , , …, , имеющие индексы i = j, и побочные реакции , , …, и т.д., у которых .
«Главные» реакции всегда положительны. Побочные реакции могут иметь любой знак и обладают свойством взаимности, т.е. .
Матрица жёсткости обладает рядом свойств:
определитель этой матрицы всегда положителен;
матрица всегда симметрична относительно главной диагонали;
произведение двух «главных» реакций всегда больше квадрата соответствующего побочного перемещения .
Для определения значений элементов матрицы реакций строят эпюры моментов от перемещений условных заделок и связей. На рис. 8.4 показаны такие эпюры, построенные для основной системы, изображённой на рис. 8.3. Значения ординат эпюр взяты из прил. 2.
В строительной механике имеются два метода определения значений элементов матрицы реакций: 1) кинематический, который основан на правиле П.Верещагина (аналогично определению перемещений) путём перемножения эпюр; 2) статический, использующий уравнения равновесия.
Наиболее рациональным методом определения реактивных усилий является статический метод. В соответствии с этим методом используют два уравнения статики — либо уравнение моментов , либо сумму проекций на ту или иную ось, например у, , сил, действующих на рассматриваемую часть основной системы метода перемещений.
Рассмотрим в качестве примера определение реактивных усилий по эпюрам, показанным на рис. 8.4.
Для определения, например, реактивного усилия , которым является изгибающий момент в условной заделке 1 от поворота этой заделки на единицу, мысленно вырежем на эпюре узел 1 (рис. 8.5, а). Реактивный момент направлен в сторону заданного перемещения Z1. Рассматривая равновесие этого узла, запишем Þ .
Реактивное усилие представляет изгибающий момент, возникающий в условной заделке 1 от поворота условной заделки 2 на единицу.
В соответствии с этим на эпюре мысленно вырежем узел 1 (см. рис. 8.5) и снова составим уравнение равновесия:
Проводя аналогичные рассуждения, нетрудно найти реактивное усилие (см. рис. 8.5, в) . В случае, если реактивным усилием является продольное усилие в условной связи (в данном случае это условная связь 3) уравнение равновесия представляет собой . Для того чтобы составить это уравнение на эпюре (эпюра ), построенной от линейного перемещения условной связи 3, мысленно делают сечение и рассматривают равновесие (рис. 8.5, г) оставшейся части рамы.
В рассматриваемом примере Þ .
Для оценки правильности вычисления коэффициентов строят суммарную единичную эпюру (см. рис. 8.4).
Произведение этой эпюры саму на себя должно давать сумму всех коэффициентов при неизвестных.
В случае невыполнения равенства (8.7) проводят построчную проверку.
Для определения свободных членов системы канонических уравнений (8.4) метода перемещений в основной системе строят так называемую грузовую эпюру , показанную на рис. 8.6.
При построении этой эпюры используют стандартные решения из прил. 3. Значения находят, используя те же методы, которые используются для определения коэффициентов . Так, для определения значения реактивного усилия мысленно вырезают узел 1, а усилия — узел 2. Из уравнений равновесия находят соответственно и . Реактивное усилие , которым в данной задаче является продольное усилие в условной связи 1, определяют, мысленно делая сечение на эпюре по стойкам близко к ригелю. Из суммы проекций на горизонтальную ось можно найти .
Проверка правильности определения значений осуществляется в соответствии с выражением
где — эпюра изгибающих моментов (рис. 8.7) от внешней нагрузки, построенная в любой статически определяемой системе, являющейся основной системой метода сил рассчитываемой заданной системы.
Решение системы канонических уравнений и построение эпюр внутренних усилий
Найденные значения коэффициентов при неизвестных и свободных членов подставляют в систему (8.4) канонических уравнений метода перемещений и решают любым известным в линейной алгебре способом.
В результате решения системы канонических уравнений метода перемещений находят значения Zi искомых перемещений. Нахождение искомых значений перемещений Zi означает, что заданная к расчёту (заданная система) стержневая конструкция становится кинематически определимой.
Все внутренние усилия, возникающие в поперечных сечениях стержней от найденных перемещений Zi и от заданной внешней нагрузки, могут быть в соответствии с принципом суперпозиции определены из выражения
Необходимым контролем правильности построения эпюры М является условие равновесия изгибающих моментов в жёстких узлах рассчитываемой конструкции. В основной системе метода перемещений единичные и грузовая эпюры являются неуравновешенными. Но единичные эпюры , будучи каждая умноженная на соответствующее ей перемещение Zi и сложенные друг с другом и грузовой эпюрой , обязательно должны в итоге давать эпюру моментов М с уравновешенными в жёстких узлах моментами. Отмеченное условие правильности построения итоговой эпюры моментов М является необходимым, но недостаточным. Достаточным условием правильности построения эпюры М является проведение деформационной проверки, суть которой изложена в разделе 6 настоящего курса. При этом не имеет значения, с использованием какого метода – метода сил или метода перемещений – построена итоговая эпюра моментов М. Поэтому для проведения деформационной проверки из заданной рассчитываемой системы выбирают любую основную систему метода сил, в которой строят любую эпюру моментов от действия неизвестной силы . Соблюдение условия свидетельствует о правильности построения эпюры М.
Построение эпюр поперечных Q и продольных N сил осуществляют точно так же, как это делается (см. раздел 6 настоящего курса) при решении статически неопределимых задач методом сил.
- Канонические уравнения метода перемещений.
- Расчёт статически неопределимых систем методом перемещений
- Страницы работы
- Фрагмент текста работы
- 1. Основные теоретические положения
- 1.1. Степень кинематической неопределимости сооружения
- 1.2. Основная система метода перемещений
- 1.3. Система канонических уравнений метода перемещений
- 1.4. Стандартные задачи метода перемещений в расчётах на прочность
- 1.5. Определение коэффициентов при неизвестных и свободных членов системы канонических уравнений
- 1.6. Определение внутренних усилий в заданном сооружении. Промежуточные и окончательные проверки правильности решения
- 1.7. Расчет статически неопределимых систем методом перемещений в матричной форме
- 2. Содержание расчетного индивидуального задания и исходные данные
- 3. Пример выполнения индивидуального задания
- 3.1. Исходные данные
- 3.2. Вычисление погонных жесткостей стержней рамы
- 3.3. Вычисление степени кинематической неопределимости и выбор основной системы метода перемещений
- 3.4. Построение деформационных схем и соответствующих им эпюр изгибающих моментов в единичных состояниях основной системы метода перемещений
- 3.5. Построение эпюр изгибающих моментов в ОСМП от внешних воздействий
- 3.6. Вычисление коэффициентов системы канонических уравнений метода перемещений
- 3.7. Проверка правильности вычисления коэффициентов системы канонических уравнений метода перемещений
- 3.8. Составление матриц для расчета рамы
- 3.9. Исходные данные для расчета рамы по программе «METDEF»
- 3.10. Результаты расчета по программе «METDEF»
- 3.11. Построение эпюр внутренних усилий в заданной раме
Видео:Основная система метода перемещенийСкачать

Канонические уравнения метода перемещений.
Канонические уравнения метода перемещений вытекают из условий эквивалентности (8.3) при использовании принципа независимости всех силовых и кинематических нагрузок, приложенных к эквивалентной системе.
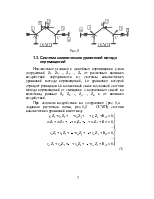
Составим первое каноническое уравнение метода перемещений для рамы с четырьмя неизвестными, используя условие 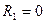
Реактивное усилие 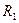
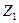
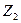
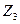
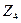
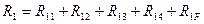
В правой части равенства (8.4) реактивные усилия имеют два индекса. Первый из них обозначает порядковый номер введенной связи эквивалентной системы, в которой усилие, а второй индекс указывает вид нагрузки, от действия которой оно возникает, т.е.:
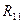
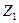
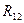
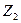
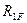
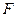
Первые четыре слагаемые правой части равенства (8.4) определяются умножением неизвестных перемещений на единичные реактивные усилия, возникающие в тех же связях основной системы, загруженной единичными перемещениями, т.е.: 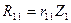
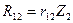
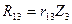
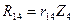
Подставим эти значения в равенство (8.4) и приравняем к нулю сумму всех слагаемых правой части, в результате получим первое каноническое уравнение метода перемещений:
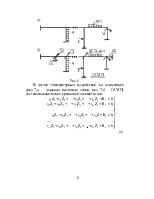
Второе и последующие уравнения составляем аналогично первому уравнению, используя второе и последующие условия эквивалентности (8.3) и принцип независимости действий внешних нагрузок. Число таких уравнений равно степени кинематической неопределимости заданной рамы, т.е. числу неизвестных метода перемещений. Все они составляют систему канонических уравнений.
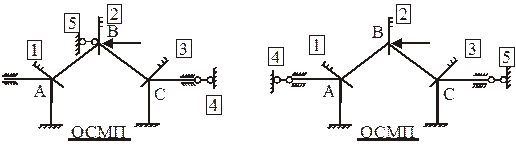
Например, для рам 1 и 2 с четырьмя неизвестными метода перемещений получаем систему четырех канонических уравнений (8.5):
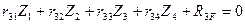
Для рамы 3 с двумя неизвестными метода перемещений составляются два канонических уравнения:
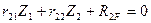
Каждое каноническое уравнение метода перемещений является отрицанием наличия реактивного момента в дополнительно введенной плавающей заделке эквивалентной системы, или реактивной сосредоточенной силы в дополнительно введенной шарнирно стержневой связи той же системы.
Обратим внимание на то, что система канонических уравнений зависит лишь от степени кинематической неопределимости рамы и не зависит от характера неизвестных метода перемещений. Но физический смысл их определяется характером вводимых связей основной системы. Так, например, для рамы 1 все четыре канонических уравнения имеют одинаковый физический смысл – отрицание наличия реактивных моментов во всех четырех дополнительно введенных плавающих заделках эквивалентной системы. Для рамы 2 два канонических уравнения (первое и третье) имеют такой же физический смысл, что и для рамы 1, а два других уравнения (второе и четвертое) отрицают наличие горизонтальных реактивных сил в дополнительно введенных шарнирно стержневых связях.
Понимание физической сущности канонических уравнений позволяет правильно установить физический смысл каждого коэффициента и свободного члена системы уравнений и выбрать рациональный метод их определения. Методы определения коэффициентов и свободных членов канонических уравнений изложены в параграфе 8.7.
Видео:Канонические уравнения метода перемещенийСкачать

Расчёт статически неопределимых систем методом перемещений
Страницы работы
Фрагмент текста работы
федеральное агентство по ОБРАЗОВАНИю РОССИЙСКОЙ ФЕДЕРАЦИИ
новосибирский государственный архитектурно-строительный университет (Сибстрин)
Кафедра строительной механики
РАСЧЁТ СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ СИСТЕМ МЕТОДОМ ПЕРЕМЕЩЕНИЙ
по выполнению индивидуального расчетного задания
по курсу «Строительная механика»
для студентов специальности 270102
«Промышленное и гражданское строительство»
Методические указания разработаны канд. техн. наук, профессором А.А. Крамаренко, ассистентом Н.Н. Сивковой
Методические указания к индивидуальному расчетному заданию «Расчет статически неопределимых систем методом перемещений» содержат необходимые теоретические положения, исходные данные и варианты индивидуального задания, пример его выполнения с использованием ЭВМ и контрольные вопросы.
Методические указания разработаны в соответствии с требованиями Государственного образовательного стандарта высшего профессионального образования к обязательному минимуму содержания и уровню подготовки инженеров по специальности 270102 «Промышленное и гражданское строительство» направления 270100 «Строительство».
Утверждены методической комиссией
факультета первой ступени высшего образования
22 мая 2008 года
— В.А. Беккер, канд. техн. наук, профессор кафедры железобетонных конструкций НГАСУ (Сибстрин);
— В.К. Фёдоров, канд. техн. наук, профессор кафедры инженерной геологии, оснований и фундаментов НГАСУ (Сибстрин)
Ó Новосибирский государственный архитектурно-строительный
университет (Сибстрин), 2008
1. Основные теоретические положения. 3
1.1. Степень кинематической неопределимости сооружения 3
1.2. Основная система метода перемещений. 5
1.3. Система канонических уравнений метода перемещений 7
1.4. Стандартные задачи метода перемещений в расчётах на прочность 10
1.5. Определение коэффициентов при неизвестных и свободных членов системы канонических уравнений. 15
1.6. Определение внутренних усилий в заданном сооружении. Промежуточные и окончательные проверки правильности решения. 17
1.7. Расчет статически неопределимых систем методом перемещений в матричной форме. 19
2. Содержание расчетного индивидуального задания и исходные данные. 25
3. Пример выполнения индивидуального задания 32
3.1. Исходные данные. 32
3.2. Вычисление погонных жесткостей стержней рамы. 33
3.3. Вычисление степени кинематической неопределимости и выбор основной системы метода перемещений. 34
3.4. Построение деформационных схем и соответствующих им эпюр изгибающих моментов в единичных состояниях основной системы метода перемещений 35
3.5. Построение эпюр изгибающих моментов в ОСМП от внешних воздействий 37
3.6. Вычисление коэффициентов системы канонических уравнений метода перемещений. 39
3.7. Проверка правильности вычисления коэффициентов системы канонических уравнений метода перемещений. 41
3.8. Составление матриц для расчета рамы. 44
3.9. Исходные данные для расчета рамы по программе «METDEF» 48
3.10. Результаты расчета по программе «METDEF». 49
3.11. Построение эпюр внутренних усилий в заданной раме 50
3.12. Проверка достоверности расчета рамы на постоянную нагрузку 53
4. Вопросы для подготовки к теоретическому собеседованию по теме индивидуального задания. 56
4.1. Расчет статически неопределимых систем методом перемещений в обычной форме на силовое воздействие. 56
4.2. Расчет статически неопределимых систем методом перемещений в обычной форме на температурные и кинематические воздействия. 57
4.3. Учет симметрии статически неопределимых сооружений при их расчете методом перемещений. 58
4.4. Расчет статически неопределимых систем методом перемещений в матричной форме на все виды внешних воздействий. 59
Список литературы. 61
Видео:основная система и канонические уравнения метода перемещенийСкачать

1. Основные теоретические положения
Видео:Перемещение | Физика 9 класс #2 | ИнфоурокСкачать

1.1. Степень кинематической неопределимости сооружения
При расчёте статически неопределимых систем методом перемещений сооружения рассматриваются как линейно-деформируемые, для которых справедлив принцип независимости действия сил и вытекающий из него принцип пропорциональности.
За неизвестные в методе перемещений принимаются перемещения узлов от заданных воздействий: линейные перемещения шарнирных и жёстких узлов и углы поворотов жёстких узлов. Суммарное количество неизвестных угловых nq и линейных перемещений узлов nD называется степенью кинематической неопределимости сооружения
Число неизвестных угловых перемещений nq равно количеству жёстких узлов сооружения.
Для сооружений, в которых перемещения от внешних воздействий обусловлены преимущественно изгибными деформациями, при определении числа линейных перемещений узлов вводятся дополнительные допущения:
1. Элементы сооружения считаются нерастяжимыми и несжимаемыми, т.е. изменением их длин под действием продольных сил пренебрегают.
2. Предполагается, что длины хорд искривлённых стержней равны их первоначальным длинам.
При этих допущениях число независимых линейных перемещений узлов сооружения nD можно определить по его шарнирной схеме, полученной из заданного сооружения введением во все его жёсткие узлы, включая и опорные, режущих цилиндрических шарниров. Степень свободы полученной таким образом шарнирной схемы будет равна числу независимых линейных перемещений узлов заданной системы. Для подсчета количества степеней cвободы плоской шарнирно-стержневой системы W используют формулу:
где У – число узлов; С – число стержней, соединяющих узлы; Со – число опорных связей.
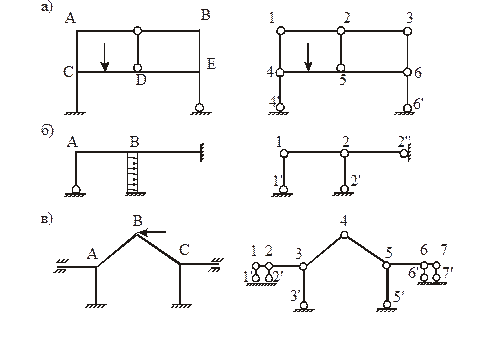
Пример. Определить степень кинематической неопределимости рам, показанных на рис. 1.
Рис. 1,а: nq = 5, так как рама имеет пять жестких узлов (A, B, C, D, E), nD = W = 2У – C – Cо = 2 × 6 – 7 – 2 = 3 (узлы шарнирной схемы 1–6; стержни, соединяющие эти узлы, 12, 23, 45, 56, 14, 25, 36; опорные связи 44′, 66′); nkin = nq + nD = 5 + 3 = 8.
Рис.1,б: nq = 2 (узлы A и B); nD = W = 2 × 2 – 1 – 3 = 0 (узлы шарнирной схемы 1 и 2; стержень, соединяющий эти узлы, 12; опорные связи 11′, 22′, 22»); nkin = 2 + 0 = 2.
Рис.1,в: nq = 3 (узлы A, B, С); nD = W = 2 × 7 – 6 – 6 = 2 (узлы шарнирной схемы 1–7; стержни, соединяющие эти узлы, 12, 23, 34, 45, 56, 67; опорные связи 11′, 22′, 33′, 55′, 66′, 77′); nkin = 3 + 2 = 5.
Видео:ЧК_МИФ: 4.1.1.ДФ_1 Физический смысл уравнений МаксвеллаСкачать

1.2. Основная система метода перемещений
Основная система метода перемещений (ОСМП) образуется наложением на узлы сооружения связей, препятствующих их угловым и линейным перемещениям. Если число наложенных на узлы угловых и линейных связей совпадает со степенью кинематической неопределимости сооружения, то в основной системе метода перемещений все узлы будут неподвижными.

Используя основную систему метода перемещений и результаты расчета стандартных стержней (см. рис. 2), определим угловые и линейные перемещения узлов заданного сооружения и внутренние усилия в нем от любых воздействий (см. п. 1.3–1.6 настоящих методических указаний).
Пример. Для рам, показанных на рис. 1, выбрать ОСМП.
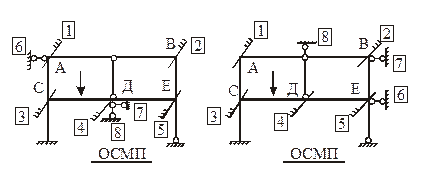
Рис. 1,а (nq = 5, nD = 3). Угловые связи 1–5 накладываются на жесткие узлы A, B, C, D, E (рис. 3). Наложение линейных связей 6–8 на узлы может быть произведено различными способами. На рис. 3 показаны два варианта размещения линейных связей 6–8. Читателям предлагается выполнить кинематический анализ шарнирной схемы рамы для каждого из вариантов основной системы метода перемещений и убедиться в правильности размещения этих линейных связей, т.е. в геометрической неизменяемости шарнирной схемы рамы.
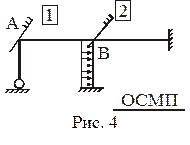
Рис. 1,в (nq = 3, nD = 2). Угловые связи 1, 2, 3 накладываются на жесткие узлы A, B, С (рис. 5). На этом же рисунке показаны два варианта наложения на узлы рамы линейных связей 4 и 5. Предпочтение следует отдать симметричному варианту размещения линейных связей. В теоретическом разделе курса «Строительная механика» показано, что использование симметричных основных систем метода перемещений существенно упрощает расчет сооружения.
Видео:Строительная механика. Расчет рамы методом перемещений. Часть 1.Скачать

1.3. Система канонических уравнений метода перемещений
Неизвестные угловые и линейные перемещения узлов сооружений Z1, Z2,…, Zj,…, Zn от различных внешних воздействий определяются из системы канонических уравнений метода перемещений, i-е уравнение которой отрицает реакцию в i-й наложенной связи в основной системе метода перемещений от смещения n наложенных связей на величины, равные Z1, Z2,…, Zj,…, Zn, и от внешних воздействий.
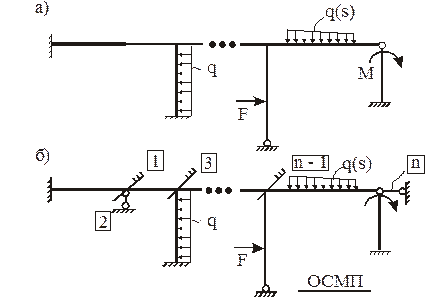
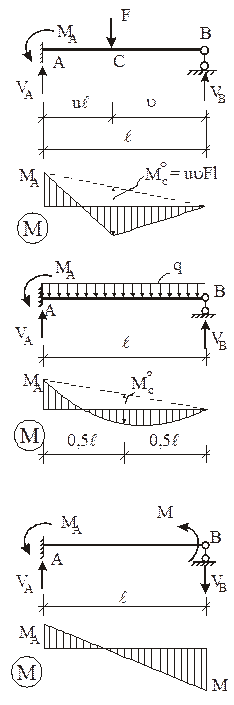
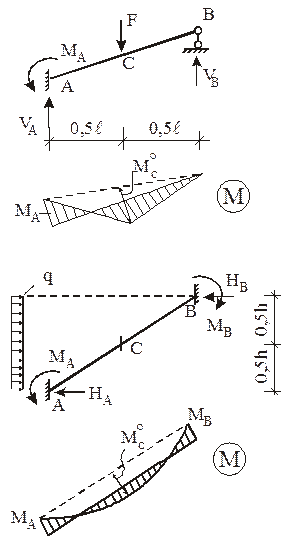
При силовом воздействии на сооружение (рис. 6,а – заданная расчетная схема, рис. 6,б – ОСМП) система канонических уравнений имеет вид:
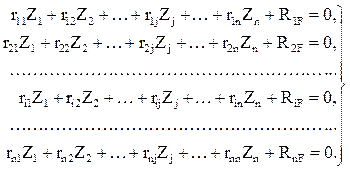
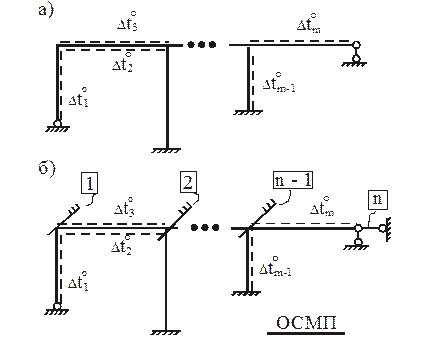
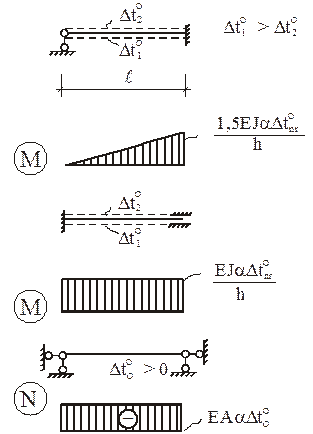
В случае температурных воздействий на сооружение (рис. 7,а – заданная расчетная схема, рис. 7,б – ОСМП) система канонических уравнений запишется так:
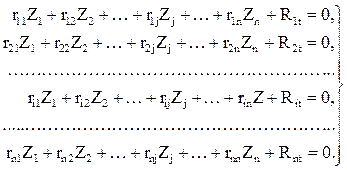
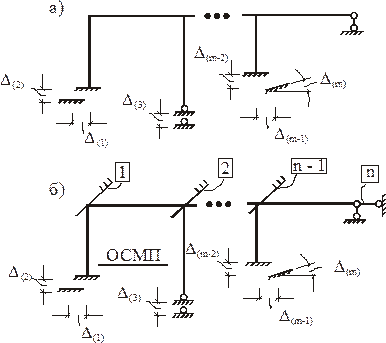
Структура системы канонических уравнений метода перемещений при кинематических воздействиях (рис. 8,а – расчетная схема сооружения при смещении опорных связей, рис. 8,б – ОСМП) сохраняется:
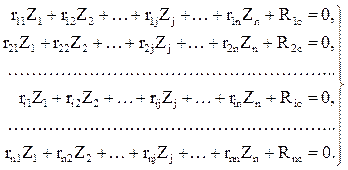
Если сооружение одновременно воспринимает воздействия различного типа (силовые, температурные, кинематические), то i-я строка системы канонических уравнений метода перемещений запишется:
В системах уравнений (3)–(5) коэффициенты при неизвестных rii называются главными, а коэффициенты rij – побочными. Физический смысл коэффициентов rii и rij – это реакции в i-й наложенной связи соответственно от смещения i-й связи на величину, равную единице, и смещения j-й связи на величину, равную единице, в основной системе метода перемещений. Побочные коэффициенты rij и rji подчиняются теореме о взаимности реакций, т.е. rij = rji.
Физический смысл свободных членов RiF, Rit, Ric систем уравнений (3)–(5) – это реакции в i-й наложенной связи соответственно от силового, температурного и кинематического воздействий в ОСМП.
Решению систем уравнений (3)–(5) предшествует вычисление коэффициентов при неизвестных rii, rij и свободных членов RiF, Rit, Ric. В методе перемещений перечисленные коэффициенты можно определить, имея эпюры внутренних усилий в основной системе от смещения наложенных связей на величины, равные единице, и от силовых, температурных и других воздействий, т.е. имея результаты расчета стандартных стержней (см. рис. 2, п. 1.2).
Видео:УСКОРЕНИЕ - Что такое равноускоренное движение? Как найти ускорение // Урок Физики 9 классСкачать

1.4. Стандартные задачи метода перемещений в расчётах на прочность
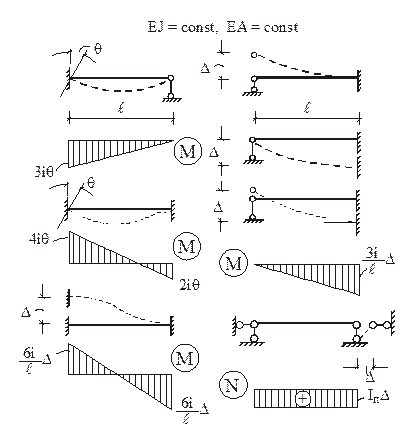
В п. 1.2 было отмечено, что основная система метода перемещений представляет собой набор стандартных задач трех типов (см. рис. 2). На различного рода воздействия (кинематические, силовые, температурные) каждый из стержней, изображенных на рис. 2, может быть заранее рассчитан, например, методом сил. Результаты этих расчетов приведены на рис. 9 (от смещения угловых и линейных связей), рис. 10–12 (от различных силовых воздействий), рис. 13 (от температурных воздействий). На указанных рисунках приняты следующие обозначения: q – поворот угловой связи; D – линейное перемещение одного конца стержня относительно другого (направление перемещений показано на рис. 9); i = EJ/ℓ – погонная жесткость стержня при изгибе; iп = = ЕА/ℓ – погонная жесткость стержня при растяжении–сжатии; 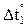
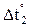
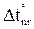
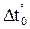
Видео:Основы метода перемещенийСкачать

1.5. Определение коэффициентов при неизвестных и свободных членов системы канонических уравнений
Коэффициенты при неизвестных rii, rij и свободные члены RiF, Rit, Ric системы канонических уравнений метода перемещений (см. соотношения (3)–(5), п. 1.3) – это реакции в i-й наложенной связи соответственно от смещения i-й и j-й наложенных связей на величину, равную единице, а также от силовых, температурных и кинематических воздействий в ОСМП. Перечисленные реакции можно определить, используя эпюры внутренних усилий (в частности, для рам и балок – эпюры изгибающих моментов), построенные в ОСМП с помощью стандартных задач (см. рис. 9–13, п.1.4).
Реакции в наложенных связях в ОСМП можно определить, используя статический или кинематический методы.
Статическим методом реакции i-й наложенной связи в ОСМП rii, rij, RiF, Rit, Ric от различного вида воздействий определяются из условий равновесия узла или любой части сооружения, содержащих рассматриваемую i-ю связь.
Для определения реакций в i-й наложенной связи в ОСМП rii, rij, RiF кинематическим методом производят сопряжение соответствующих эпюр изгибающих моментов:
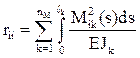
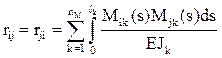
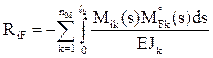
где EJk – изгибная жесткость поперечного сечения на k-м грузовом участке рассматриваемого сооружения (часто EJk = const);
ℓk – длина k-го грузового участка;
nM – общее число грузовых участков;
Mik и Mjk – изгибающие моменты на k-м грузовом участке в ОСМП соответственно от смещения i-й и j-й наложенных связей на величину, равную единице;
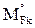
Вычисление коэффициентов rii, rij, RiF по формулам (8)–(10) можно произвести сопряжением соответствующих эпюр изгибающих моментов, используя формулу Симпсона или правило Верещагина.
Ниже, в п. 1.7, будет рассмотрено определение коэффициентов при неизвестных и свободных членов системы канонических уравнений метода перемещений в матричной форме.
Видео:Метод Перемещений с 2-мя неизвестнымиСкачать

1.6. Определение внутренних усилий в заданном сооружении. Промежуточные и окончательные проверки правильности решения
На данном этапе расчета стержневых систем методом перемещений мы имеем эпюры изгибающих моментов M1, M2,…, Mj,…, Mn, 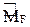
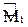
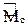
MF = M1Z1 + M2Z2 + … + MjZj + … + MnZn + 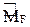
Mt = M1Z1 + M2Z2 + … + MjZj + … + MnZn + 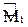
Mc = M1Z1 + M2Z2 + … + MjZj + … + MnZn + 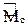
Поперечные и продольные силы в сечениях заданной системы вычислим по эпюрам изгибающих моментов из условий равновесия отдельных элементов и узлов, используя методику, изложенную в п. 5.4 первой части лекций по строительной механике [5].
Многоэтапность расчета статически неопределимых сооружений методом перемещений требует проведения проверок достоверности вычисления коэффициентов системы канонических уравнений, правильности решения этой системы уравнений, а также окончательной проверки эпюр внутренних усилий, полученных в результате расчета.
Главные и побочные коэффициенты rii и rij систем канонических уравнений (3)–(5) могут быть вычислены двумя способами: статическим (из условий равновесия узлов) и кинематическим (сопряжением соответствующих эпюр изгибающих моментов, построенных в ОСМП от единичных кинематических воздействий). Кроме того, правильность вычисления любого побочного коэффициента rij может быть подтверждена независимым определением равного ему побочного коэффициента rji [7, п. 15.3].
Правильность вычисления свободных членов RiF системы канонических уравнений метода перемещений (3) можно подтвердить вычислением их двумя методами: статическим и кинематическим. При этом, используя соотношение (10), необходимо помнить, что грузовая эпюра изгибающих моментов 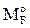
При необходимости можно произвести универсальную и построчные проверки правильности вычисления коэффициентов при неизвестных систем канонических уравнений (3)–(5), а также проверку достоверности определения свободных членов системы уравнений (3). Для этого (как и в методе сил [7, п. 16.5]) используют суммарную эпюру изгибающих моментов Ms, полученную в ОСМП суммированием эпюр изгибающих моментов от единичных кинематических воздействий:
С помощью эпюры изгибающих моментов Ms получим:
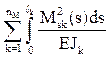
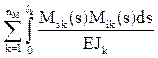
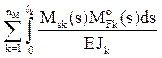
На заключительном этапе расчета производится проверка правильности эпюр внутренних усилий, построенных в заданном статически неопределимом сооружении. Если при решении задачи ошибки отсутствовали, то узлы заданного сооружения и любые его части должны находиться в равновесии. Это следует из того, что в заданном сооружении нет связей, в которых отрицались реакции в ОСМП [8, п. 19.3].
Дополнительно для окончательной проверки эпюр внутренних усилий, полученных для заданного сооружения от силового воздействия, можно использовать любую, желательно статически определимую, основную систему метода сил, для которой должны выполняться кинематические условия:
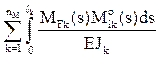
В соотношении (18) MF(s) – изгибающие моменты от силового воздействия в заданном сооружении, вычисленные методом перемещений, 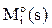
Видео:Вселенная от начала до черных дыр.Скачать

1.7. Расчет статически неопределимых систем методом перемещений в матричной форме
Системы канонических уравнений метода перемещений (3)–(5) могут быть представлены одним матричным соотношением:
где r – матрица коэффициентов при неизвестных системы канонических уравнений метода перемещений, или матрица реакций в наложенных связях от их смещения на величину, равную единице, в ОСМП. Эта матрица называется матрицей внешней жесткости сооружения:
r = 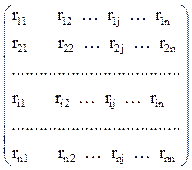
Число строк и столбцов матрицы внешней жесткости сооружения равно степени его кинематической неопределимости nkin, т.е. матрица r – квадратная. В силу теоремы о взаимности реакций матрица r симметрична. Так как системы канонических уравнений метода перемещений (3)–(5) разрешимы, то определитель матрицы r не равен нулю (det r ¹ 0). Это значит, что матрица внешней жесткости сооружения – невырожденная матрица.
Z – матрица неизвестных метода перемещений, или матрица угловых и линейных перемещений узлов сооружения от заданных внешних воздействий (силовых, температурных, кинематических).
R – матрица свободных членов системы канонических уравнений метода перемещений, или матрица реакций в наложенных связях от заданных внешних воздействий в ОСМП.
Число строк в матрицах Z и R равно степени кинематической неопределенности сооружения, а число столбцов – суммарному числу заданных независимых силовых, температурных и кинематических воздействий на сооружение.
В [7, п. 22.2, лекция 22] на базе теоремы о работе концевых усилий были получены матричные соотношения для вычисления элементов матриц r и R в ОСМП:
R = a T 
Конкретизируем содержание элементов матриц, входящих в выражения (21) и (22).
а – матрица концевых перемещений элементов стержневой системы (стержней) – углов поворота их концевых сечений qj и qh, а также перекосов стержней Djh, вызванных смещением наложенных угловых и линейных связей на величину, равную единице, в ОСМП. Число столбцов матрицы а равно степени кинематической неопределенности сооружения.
K – матрица внутренней жесткости сооружения. Ее элементы – концевые усилия отдельных стержней (концевые изгибающие моменты и поперечные силы), полученные от единичных перемещений концевых сечений этих стержней в ОСМП. Для всего сооружения матрица K запишется:
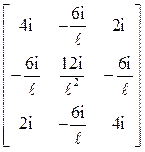
В квазидиагональной матрице (23) блок Kj – стандартная матрица внутренней жесткости j-го стержня. Если изгибающие моменты и поперечные силы фиксировать так, как показано на рис. 14,а, б для стандартных стержней, то матрицы Kj будут иметь вид:
Kj = 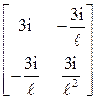
R – матрица реакций в наложенных связях от внешних воздействий в ОСМП:
Здесь RF, Rt, Rc – подматрицы реакций в наложенных связях соответственно от силовых, температурных и кинематических воздействий в ОСМП. Число столбцов матричных блоков RF, Rt, Rc определяется числом комбинаций указанных типов воздействий.

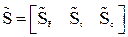
F’ – матрица узловых нагрузок:
В этой матрице отличными от нуля будут элементы только блока F, описывающего силовое воздействие на сооружение. Блоки, соответствующие температурным и кинематическим воздействиям, будут нулевыми. При формировании блока F матрицы F’ равнодействующую нагрузки, приложенной к отдельному стержню jh, передают узлу h, т.е. узлу, противоположно расположенному сечению j, где при формировании матрицы 
с – матрица углов поворота и линейных перемещений узлов в ОСМП от смещения наложенных на узлы сооружения связей на величину, равную единице. Число столбцов матрицы с равно степени кинематической неопределенности сооружения.
Решая систему уравнений (19), получим матрицу неизвестных метода перемещений:
где r –1 – матрица, обратная к матрице внешней жесткости сооружения, т.е.
r × r –1 = E, здесь Е – единичная матрица.
После подстановки соотношений (21) и (22) в матричное выражение (24) получим:
Z = –(a T Ka) –1 (a T 
Матрицу концевых изгибающих моментов и поперечных сил
в заданном сооружении от внешних силовых, температурных и кинематических воздействий получим, используя принцип независимости действия сил
S = 
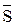
В матричном соотношении (26) 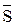
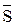
где K – матрица концевых усилий стержней от единичных перемещений их концевых сечений в ОСМП (см. (21)). Выше было показано, что при определенной нумерации концевых сечений стержней и при определенном порядке записи концевых изгибающих моментов и поперечных сил (см. рис. 14), матрицы K для отдельных элементов имеют стандартную структуру.
После подстановки в соотношение (26) матричных выражений (25) и (27) получим матричную формулу для расчета стержневых систем методом перемещений:
S = 

При силовом воздействии на сооружение, когда S = SF, 

SF = 

В случае температурного воздействия S = St, 

St = 

При кинематическом воздействии, в частности, при смещении опорных связей, матричная зависимость для определения концевых усилий в стержнях заданного сооружения аналогична матричной зависимости (30):
Sс = 

Проверка правильности расчета заданного сооружения методом перемещений в матричной форме производится на основе теоремы о работе концевых усилий:
– в общем случае внешних воздействий
a T S – c T F’ = 0;
– при силовых воздействиях
a T SF – c T F = 0;
– при температурных и кинематических воздействиях
Для расчета стержневых систем методом перемещений на персональных ЭВМ может быть использована программа «METDEF» , разработанная на кафедре строительной механики НГАСУ (Сибстрин) профессором В.Г. Себешевым и доцентом В.Н. Барышниковым.
Видео:канонические уравнения метода силСкачать

2. Содержание расчетного индивидуального задания и исходные данные
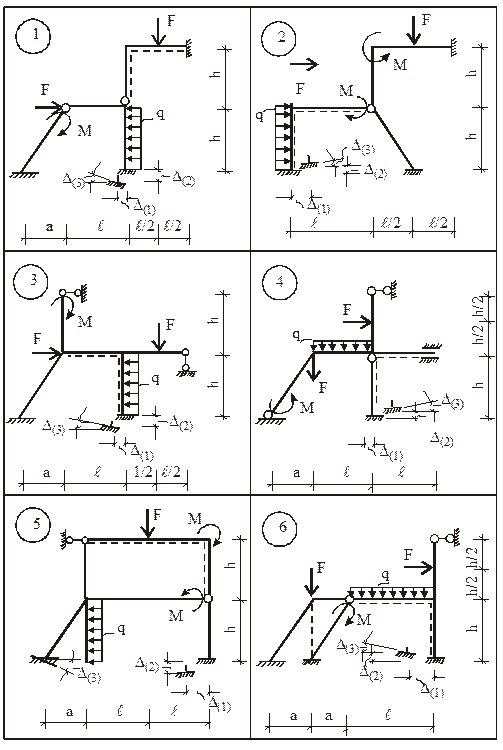
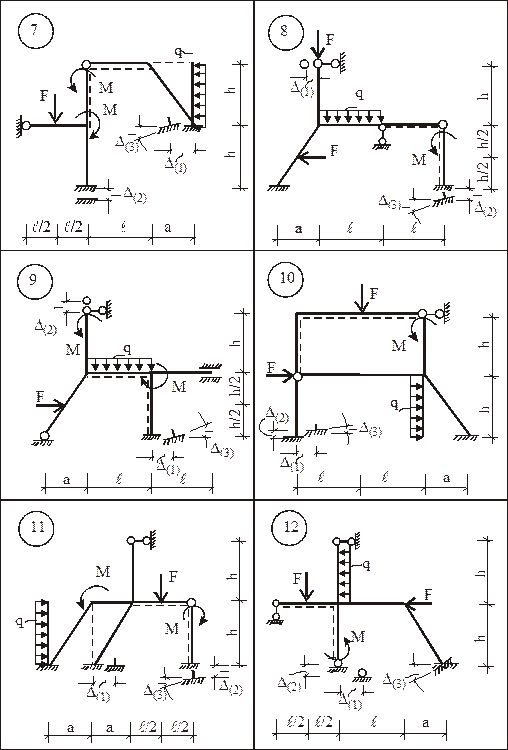
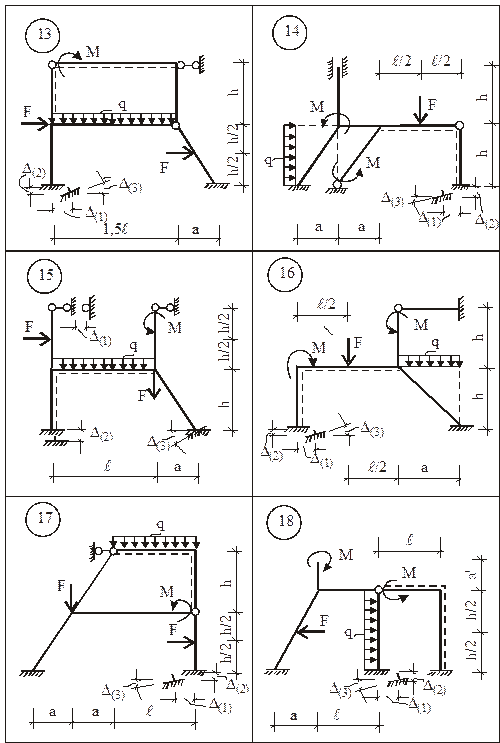
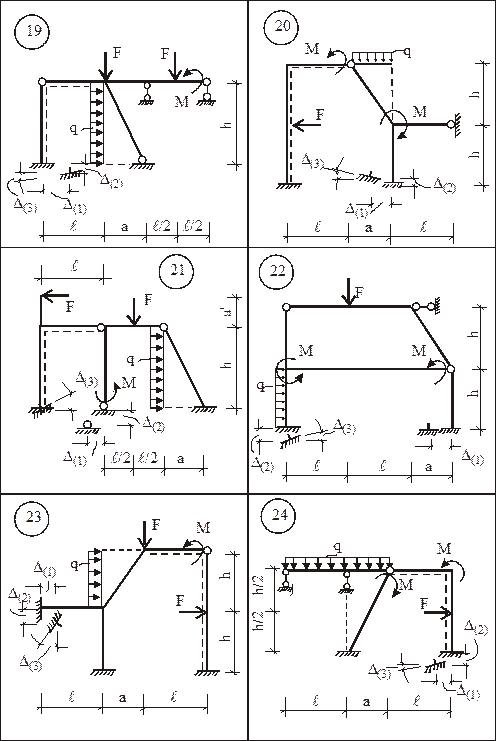
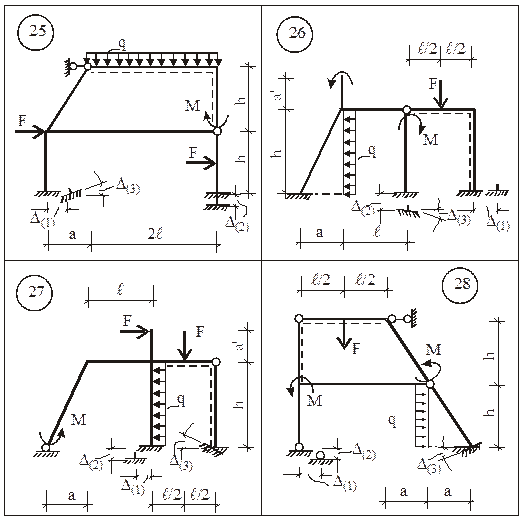
Для заданной статически неопределимой рамы (рис. 15) требуется:
1. Определить степень кинематической неопределимости рамы и выбрать для ее расчета ОСМП.
2. В ОСМП построить деформационные схемы и соответствующие им эпюры изгибающих моментов от смещения каждой наложенной связи на величину, равную единице, и отдельно от каждого из внешних воздействий (силового, температурного, смещения опорных связей).
3. Вычислить коэффициенты при неизвестных и свободные члены системы канонических уравнений метода перемещений (только при воздействии постоянной нагрузки).
4. Выполнить проверку правильности вычислений коэффициентов при неизвестных и свободных членов системы канонических уравнений метода перемещений:
а) rii – сопряжением соответствующих эпюр изгибающих моментов;
б) rij – с помощью теоремы о взаимности реакций;
в) RiF – с использованием статически определимой основной системы метода сил.
5. Подготовить исходные данные и матрицы для расчета рамы на ЭВМ по программе «METDEF».
6. По результатам расчета на ЭВМ построить в заданной раме эпюры M, Q и N от постоянной нагрузки, температурных воздействий и смещения опорных связей (отдельно).
7. Выполнить статическую и кинематическую проверки правильности построенных эпюр внутренних усилий от постоянной нагрузки.
Исходные числовые данные для индивидуального расчета задания приведены в табл. 1.
Примечания. 1. EI1 и h1 – жесткость при изгибе и высота прямоугольного поперечного сечения горизонтальных элементов рамы.
2. EI2 и h2 – жесткость при изгибе и высота прямоугольного поперечного сечения вертикальных и наклонных элементов рамы.
3. Поперечное сечение всех элементов рамы симметрично относительно плоскости изгиба.
4. Изменение температуры на Dt° происходит на отмеченных штриховыми линиями поверхностях стержней.
5. Для всех вариантов принять: a = 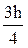
Рис. 15 (продолжение)
Рис. 15 (продолжение)
Рис. 15 (продолжение)
Рис. 15 (окончание)
Видео:Физический смысл производной с НУЛЯ /подробно и легкоСкачать

3. Пример выполнения индивидуального задания
Видео:Как распознать талантливого математикаСкачать

3.1. Исходные данные
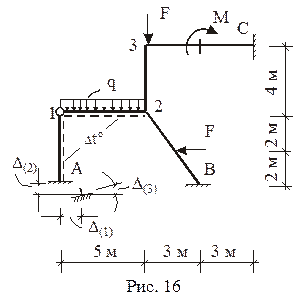
Рама испытывает следующие независимые друг от друга внешние воздействия:
1. Силовое (постоянная нагрузка): q = = 24 кН/м, F = 36 кН, М = 60 кН×м.
2. Изменение температуры Dt° = 60 °С на поверхности стержней, отмеченных пунктирной линией.
3. Смещение опорных связей: D(1) = 2 см, D(2) = 1 см, D(3) = 0,001 рад.
Изгибные жесткости прямоугольных поперечных сечений элементов рамы в плоскости изгиба рамы: EJ1 – для горизонтальных стержней, EJ2 – для вертикальных и наклонного стержней; высоты поперечных сечений: h1 = 0,3 м – для горизонтальных стержней, h2 = 0,4 м – для вертикальных и наклонного стержней.
Дополнительные исходные данные: EJ1 : EJ2 = 2, EJ1 = 3×10 4 кН×м 2 , EJ2 = 1,5×10 4 кН×м 2 ; коэффициент линейного температурного расширения материала a = 12×10 –6 1/°С.
Видео:Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать

3.2. Вычисление погонных жесткостей стержней рамы
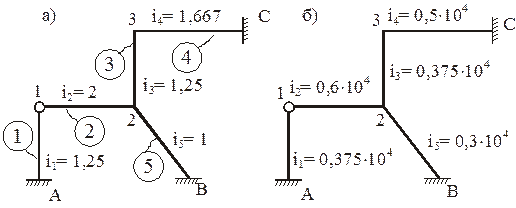
А) В расчете на силовое воздействие учитываем относительные значения изгибных жесткостей поперечных сечений элементов рамы (рис. 17,а):
i1 = 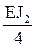
i2 = 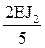
i3 = 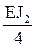
i4 = 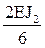
i5 = 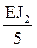
Погонную жесткость стержня 2В (рис. 17,а) примем равной единице (i5 = 1) и выразим погонные жесткости остальных стержней через i5.
Б) В расчетах на температурное воздействие и смещение опорных связей обязателен учет абсолютных значений изгибных жесткостей поперечных сечений элементов рамы (рис. 17,б):
i1 = 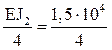
i2 = 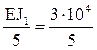
i3 = 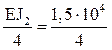
i4 = 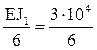
i5 = 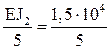
Видео:7.5 ЧАСОВ МАТАНА!!! ПОДАРОК ВСЕМ СТУДЕНТАМ ДЛЯ ПОДГОТОВКИ К ЗАЧЁТАМ И ЭКЗАМЕНАМ ОТ ЁЖИКА В МАТАНЕ!!!Скачать

3.3. Вычисление степени кинематической неопределимости и выбор основной системы метода перемещений
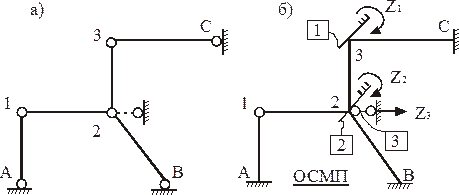
Для заданной рамы nkin = nq + nD = 2 + 1 = 3. Число неизвестных угловых перемещений узлов рамы nq = 2 (узлы 3 и 2 – рис. 16). Число независимых линейных перемещений узлов рамы определим по ее шарнирной схеме (рис. 18,а). Степень свободы полученной шарнирной схемы W = 2У – C – Cо = 2×3 – 2 – 3 = 1, следовательно nD = 1. Правильное наложение одной линейной связи на узлы нашей шарнирной схемы должно обеспечить ее геометрическую неизменяемость (рис. 18,а)
ОСМП образована наложением двух угловых связей («плавающих» заделок) на узлы 3 и 2 и одной линейной горизонтальной связи на узел 2 (рис. 18,б). За неизвестные в расчете данной рамы приняты: углы поворотов узлов 3 и 2 – Z1 и Z2 и горизонтально перемещение узла 2–Z3. Эти неизвестные определим из системы канонических уравнений метода перемещений, которая в общем случае силового воздействия запишется:
Видео:Квантовая телепортация во Вселенной.Скачать

3.4. Построение деформационных схем и соответствующих им эпюр изгибающих моментов в единичных состояниях основной системы метода перемещений
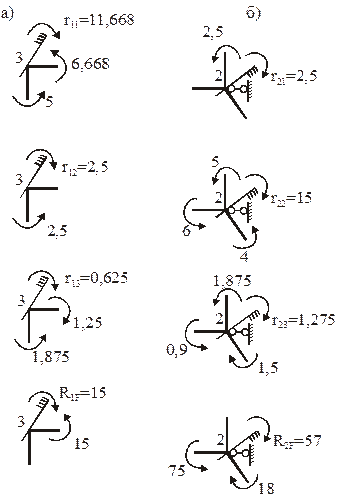
Деформационные схемы стержней рамы в ОСМП, построенные от поворота первой и второй наложенных угловых связей по часовой стрелке на величину, равную единице, показаны на рис. 19,а, б.
Деформационную схему рамы в ОСМП от единичного смещения линейной связи вправо (рис. 19,в) получим, предварительно построив план перемещений узлов рамы (рис. 19,г). Поместив в полюсе полярного плана перемещений неподвижные точки А, В, С, зададим перемещение узлу 2 в направлении, перпендикулярном оси стержня 2В. Зная линейное перемещение узла 2, последовательно определим перемещения узлов 1 и 3. Проекцию истинного перемещения узла 2 на горизонтальную ось принимаем равной единице. По плану перемещений, используя элементарные геометрические и тригонометрические положения, определим перекосы элементов рамы: D1A = D23 = 1, D12 = D3C = = 0,75, D2B = 1,25 (рис. 19,в, г).
Эпюры изгибающих моментов от единичных смещений наложенных связей в ОСМП изображены рядом с соответствующими деформационными схемами на рис. 19,а, б, в. Для их построения использованы стандартные задачи метода перемещений от кинематических воздействий (см. рис. 9).
Видео:Расчет рамы методом перемещений. СтроймехСкачать

3.5. Построение эпюр изгибающих моментов в ОСМП от внешних воздействий
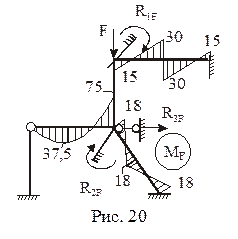
На рис. 20 изображена эпюра изгибающих моментов MF в ОСМП от постоянной нагрузки. Необходимо помнить, что в ОСМП от узловых нагрузок эпюра изгибающих моментов отсутствует (в нашем случае от вертикальной силы F, приложенной к узлу 3). На рис. 21 и 22 даны подробные пояснения к построению эпюр изгибающих моментов в ОСМП от заданного изменения температуры (Mt) и от смещения опорных связей (Мс). Напоминаем, что эпюра изгибающих моментов Mt = M’t + M»t, где M’t – эпюра изгибающих моментов от равномерных приращений температуры D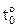
Видео:Закон БернуллиСкачать

3.6. Вычисление коэффициентов системы канонических уравнений метода перемещений
Коэффициенты при неизвестных и свободные члены системы канонических уравнений метода перемещений вычислим статическим методом. Используем для этого эпюры изгибающих моментов М1, М2, М3 (см. рис. 19), построенные в ОСМП от единичных смещений наложенных связей, а также эпюру изгибающих моментов MF, полученную в ОСМП от постоянной нагрузки (см. рис. 20). Рис. 23,а поясняет вычисление в ОСМП реакций в первой наложенной связи r11, r12, r13, R1F от поочередного смещения всех наложенных связей на величину, равную единице, и от постоянной нагрузки; рис. 23,б – реакций во второй наложенной связи r21, r22, r23, R2F от тех же воздействий. Так как наложенные связи 1 и 2 угловые, то при вычислении реакций в них учитываем только изгибающие моменты в концевых сечениях стержней.
По этой причине на рис. 23 при изображении отдельных узлов мы не показываем поперечных и продольных сил в сечениях около узлов.
Вычисление реакций r31, r32, r33, R3F в линейной связи 3 проиллюстрировано на рис. 24. Любую из этих реакций вычисляем в следующей последовательности: из равновесия узла 1 находим продольную силу N12 в стержне 12; из равновесия узла 3 вычислим продольную силу N32 в стержне 32; определяем требуемую реакцию из равновесия узла 2. На рис. 24 не показаны изгибающие моменты в сечениях около узлов, так как в условия равновесия в форме проекций сил на какие-то оси они не входят.
Видео:С.М. Задача №8.1 расчёт рамы на устойчивость методом перемещенийСкачать

3.7. Проверка правильности вычисления коэффициентов системы канонических уравнений метода перемещений
Побочные коэффициенты при неизвестных системы канонических уравнений метода перемещений rij в п. 3.6 были вычислены статическим методом. Достоверность их определения подтверждается теоремой о взаимности реакций. Из рис. 23 и 24 видно, что r12 = r21, r13 = r31, r23 = r32.
Вычисление главных коэффициентов при неизвестных системы канонических уравнений метода перемещений для проверки произведем повторно кинематическим методом.
r11 =
+
r22 =
+
r33 =
+
+
Приведенные вычисления показывают, что значения главных коэффициентов r11, r22, r33, ранее вычисленные статическим методом (см. рис. 23 и 24) и результаты вышеперечисленных сопряжений эпюр изгибающих моментов М1, М2, М3 (см. рис. 19) совпадают. Следует заметить, что изгибные жесткости поперечных сечений элементов рамы привязаны к принятым в п. 3.2 значениям погонных жесткостей:
Проверку свободных членов системы канонических уравнений метода перемещений, т.е. грузовых коэффициентов, ранее полученных статическим методом в п. 3.6 (см. рис. 23, 24) произведем кинематическим методом, используя статически определимую основную систему метода сил (рис. 25,а) и эпюру изгибающих моментов, построенную в ней, от постоянной нагрузки 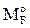
R1F = –
+
R2F = –
+
R3F = –
–
+
+
Результаты вышеприведенных сопряжений эпюр изгибающих моментов М1, М2, М3 с эпюрой М 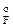
3.8. Составление матриц для расчета рамы
Для расчета статически неопределимых систем методом перемещений на многовариантные внешние воздействия, включающие силовые, температурные и смещение опорных связей, используется матричное соотношение (28):
S = 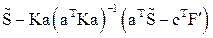
Составлению матриц а и 

Используя деформационные схемы рамы в единичных состояниях ОСМП, формируем матрицу а – матрицу поворотов концевых сечений стержней и их перекосов от единичных смещений наложенных связей. Правило знаков при составлении матрицы а: повороты концевых сечений, в случае если они происходят по часовой стрелке, считаются положительными и отрицательными, – если против хода часовой стрелки. Перекос j-го элемента Djh положителен, если поворот хорды, стягивающей его концы, по отношению к первоначальному положению оси стержня происходит по ходу часовой стрелки, и отрицателен, – если против хода часовой стрелки.
Матрица концевых усилий 




Элементы каждого из блоков матрицы 
Для формирования матрицы 

Матрица узловых нагрузок F’ от заданных воздействий на раму имеет вид:
F’ = [F 0 0], где F – матрица узловых нагрузок, входящих в состав силового воздействия. Нулевые блоки описывают температурные и кинематические воздействия, не имеющих силовых потенциалов.
В матрицу F помимо непосредственно действующих силовых нагрузок (сосредоточенных моментов и сосредоточенных сил) в соответствии с теоремой о работе концевых усилий включаются равнодействующие нагрузок, приложенных к стержням 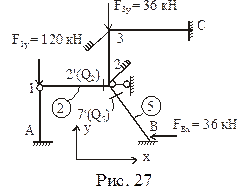

Формирование матрицы F производим, последовательно обходя узлы в установленном нами порядке: А, 1, 2, 3, С, В. Для каждого узла первым записываем сосредоточенный момент (если он имеется), второй – горизонтальную сосредоточенную силу, третьей – вертикальную сосредоточенную силу. Знак сосредоточенных сил привязывает к принятой системе координат (см. рис. 27). Сосредоточенный узловой момент, действующий по ходу часовой стрелки, считается положительным, против хода часовой стрелки – отрицательным. При отсутствии в рассматриваемом узле каких-либо компонент узловой нагрузки их нулевые значения в матрице F фиксировать не будем.
F’ = 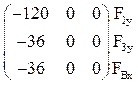
Матрицу угловых и линейных перемещений узлов с в ОСМП, вызванных единичным смещением наложенных связей, удобно формировать после составления блока F матрицы F’, используя деформационные схемы рамы и план перемещений ее узлов (см. рис. 19). Знаки линейных узловых перемещений привязываем к принятой системе координат (см. рис. 27), повороты узлов по ходу часовой стрелки считаем положительными. Первый столбец матрицы с описывает вертикальные перемещения узла 1, вертикальное перемещение узла 3 и горизонтальное перемещение узла В от поворота первой наложенной связи на величину, равную единице; второй столбец – эти же перемещения от единичного поворота второй наложенной связи; третий – то же от единичного смещения линейной связи в ОСМП.
Выше уже упоминалось, что матрицы внутренней жесткости отдельных элементов рамы Kj по программе «METDEF» формируются автоматически, если исходные данные, введенные в компьютер, содержат указание типа стандартного стержня, его погонную жесткость и длину.
3.9. Исходные данные для расчета рамы по программе «METDEF»
Степень кинематической неопределимости системы – 3.
Число элементов ОСМП – 5.
Суммарное число перемещений концевых сечений элементов ОСМП – 13.
Число вариантов заданных воздействий – 3.
Число перемещений узлов системы, к которым приложена нагрузка – 3.
Длины элементов – 4, 5, 4, 6, 5.
Отношения погонных жесткостей элементов – 1.25, 2, 1.25, 1.667, 1.
Типы элементов – 2, 2, 1, 1, 1.
[а] – матрица перемещений концевых сечений элементов ОСМП в единичных состояниях (матрица транспонирована):
0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0
(в строку записывается первый столбец матрицы а, затем аналогично второй и третий).
[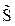
0, 0, 75, – 75, 0, 0, 0, 15, –15, 15, –18, 14.4, 18
(в строку записывается первый столбец матрицы 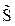
[с] – матрица смещений узлов в единичных состояниях ОСМП (матрица транспонирована):
[F] – матрица узловых нагрузок по вариантам заданных воздействий (матрица транспонирована):
3.10. Результаты расчета по программе «METDEF»
На печать выдаются следующие расчетные параметры:
1. Матрица [r] внешней жесткости ОСМП (коэффициенты при неизвестных системы канонических уравнений метода перемещений):
r =
2. Матрица [R] свободных членов системы канонических уравнений перемещений по вариантам воздействий:
R =
3. Матрица [Z] основных неизвестных метода перемещений по вариантам воздействий:
Z =
4. Матрица [S] усилий в концевых сечениях элементов заданной системы по вариантам воздействий:
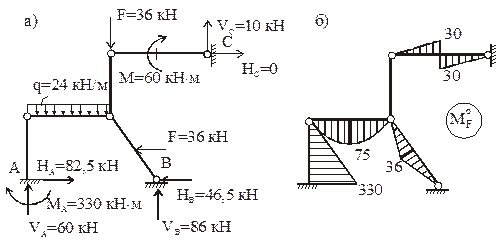
3.11. Построение эпюр внутренних усилий в заданной раме
Используя элементы матрицы S и округляя их до сотых, строим эпюры изгибающих моментов в заданной раме:
Mconst – от постоянной нагрузки (рис. 28,а);
MT – от изменений температуры (рис. 28,б) и MD – смещения опорных связей (рис. 28,в).
По эпюрам изгибающих моментов Мconst, МT, МD, частично используя данные матрицы S о концевых поперечных силах в сечениях 1, 2, 3, 5, 7 рамы и вычисляя недостающие ординаты эпюры поперечных сил Qconst в левом