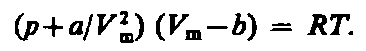Читайте также:
|
| р, атм | pV, атм·л | , атм·л |
|---|---|---|
| 1 | 1,000 | 1,000 |
| 100 | 0,994 | 1,000 |
| 200 | 1,048 | 1,009 |
| 500 | 1,390 | 1,014 |
| 1000 | 2,069 | 0,893 |
Как видно из Табл. 2.2.1, уравнение Ван-дер-Ваальса гораздо лучше согласуется с экспериментом. Уравнение (2.2.5) можно представить так:
Получилось кубическое уравнение относительно неизвестной V, коэффициенты которого зависят от давления и температуры. Такое уравнение со свободным членом и вещественными коэффициентами имеет три решения, причем в зависимости от соотношения между коэффициентами либо все три решения будут вещественными, либо одно решение — вещественным, а два других — комплексными. Поскольку объем может быть только вещественной величиной, комплексные решения не имеют физического смысла. На Рис. 2.2.2 показаны изотермы Ван-дер-Ваальса для нескольких значений температур.
Рис. 2.2.2. Изотермы Ван-дер-Ваальса
При температуре Т’ и давлениях в пределах p’1 до p’2 коэффициенты в уравнении (2.2.6) таковы, что все три решения оказываются вещественными; при иных давлениях вещественным будет только одно решение. Начиная с определенной, своей для каждого вещества температуры Ткр ( критической температуры ) при любом давлении вещественным остается только одно решение уравнения (2.2.6). Если повышать температуру, то точки, соответствующие решениям уравнения V’1, V’2, V’3, все больше сближаются, сливаясь при критической температуре в одну точку К, также называемую критической точкой . Для соответствующей изотермы точка К является точкой перегиба. Ей соответствуют три совпадающих вещественных решения уравнения (2.2.6). Касательная к критической изотерме в точке К будет параллельна оси V, так что в этом случае производная . Кроме того, в точке перегиба должна быть равна нулю и вторая производная .
Разрешим уравнение (2.2.1) относительно р:
Дифференцирование (2.2.7) по объему дает:
| (2.2.8) |
| (2.2.9) |
В критической точке, т.е. при подстановке Т = Ткр, Vкм = Vкм.кр, эти выражения должны обращаться в нуль:
| (2.2.10) |
| (2.2.11) |
Совместно с (2.2.7), записанным для точки К:
они образуют три уравнения с тремя неизвестными ркр, Vкм.кр и Ткр. Решение этой системы уравнений дает:
Таким образом, зная константы Ван-дер-Ваальса а и b, можно найти соответствующие критической точке параметры ркр, Vкм.кр и Ткр, которые называются критическими величинами . И, наоборот, по известным критическим величинам могут быть найдены значения констант Ван-дер-Ваальса. Из (2.2.13) и (2.2.12) можно получить:
в то время как согласно уравнению состояния идеального газа должно было бы выполняться соотношение:
2.2.2. Внутренняя энергия реального газа
Взаимодействие между молекулами реального газа обусловливает их взаимную потенциальную энергию, которая должна учитываться во внутренней энергии газа наряду с кинетической энергией движения молекул:
Кинетическая энергия киломоля газа равна:
и прямо пропорционально зависит от температуры.
Потенциальная энергия взаимодействия молекул зависит от среднего расстояния между ними, поэтому Еп должна быть функцией объема газа V. Следовательно, внутренняя энергия газа есть функция двух параметров — температуры и объема:
При расширении газа совершается работа по преодолению сил притяжения между молекулами. Работа против внутренних сил, действующих между молекулами киломоля газа, может быть записана в виде:
Приравнивая (2.2.19) приращению потенциальной энергии, получим:
Интегрируя (2.2.20), имеем:
Значение постоянной интегрирования полагают равной нулю, что при увеличении объема газа до бесконечности соответствует отсутствию взаимодействия между молекулами газа. Тогда полное выражение для внутренней энергии киломоля реального газа будет иметь вид:
Из (2.2.22) следует, что внутренняя энергия растет как при повышении температуры, так и при увеличении объема.
Если газ будет расширяться или сжиматься без теплообмена с внешней средой и без совершения над ним внешней работы, то, согласно первому началу термодинамики, его внутренняя энергия должна оставаться постоянной. Тогда из (2.2.22) получим:
из чего следует, что приращения dT и dVкм имеют противоположный знак.
Следовательно, при расширении в таких условиях газ всегда должен охлаждаться, а при сжатии — нагреваться.
© ФГОУ ВПО Красноярский государственный аграрный университет, 2015
Видео:Уравнение Ван-дер-Ваальса | Газы.Молекулярно-кинетическая теория | Химия (видео 8)Скачать

Физический смысл констант а и b в уравнении ван дер ваальса
Предпринималось много попыток для учета отклонений свойств реальных газов от свойств идеального газа путем введения различных поправок в уравнение состояния идеального газа. Наибольшее распространение вследствие простоты и физической наглядности получило уравнение Ван-дер-Ваальса (1873).
Первая поправка в уравнении состояния идеального газа рассматривает собственный объем, занимаемый молекулами реального газа. В уравнении Дюпре (1864)
постоянная b учитывает собственный мольный объем молекул.
При понижении температуры межмолекулярное взаимодействие в реальных газах приводит к конденсации (образование жидкости). Межмолекулярное притяжение эквивалентно существованию в газе некоторого внутреннего давления 

(p + 
Ван-дер-Ваальс в 1873 г. дал функциональную интерпретацию внутреннего давления. Согласно модели Ван-дер-Ваальса, силы притяжения между молекулами (силы Ван-дер-Ваальса) обратно пропорциональны шестой степени расстояния между ними, или второй степени объема, занимаемого газом. Считается также, что силы притяжения суммируются с внешним давлением. С учетом этих соображений уравнение состояния идеального газа преобразуется в уравнение Ван-дер-Ваальса:
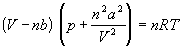
или для одного моля
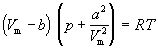
Значения постоянных Ван-дер-Ваальса a и b, которые зависят от природы газа, но не зависят от температуры, приведены в таблице 1.3.
Таблица 1.3. Постоянные Ван-дер-Ваальса для различных газов
| Газ | a, л 2 *бар* моль -2 | b,см 3 * моль -1 | Газ | a, л 2 * бар* моль -2 | b, см 3 * моль -1 |
| He | 0,03457 | 23,70 | NO | 1,358 | 27,89 |
| Ne | 0,2135 | 17,09 | NO2 | 5,354 | 44,24 |
| Ar | 1,363 | 32,19 | H2O | 5,536 | 30,49 |
| Kr | 2,349 | 39,78 | H2S | 4,490 | 42,87 |
| Xe | 4,250 | 51,05 | NH3 | 4,225 | 37,07 |
| H2 | 0,2476 | 26,61 | SO2 | 6,803 | 56,36 |
| N2 | 1,408 | 39,13 | CH4 | 2,283 | 42,78 |
| O2 | 1,378 | 31,83 | C2H4 | 4,530 | 5,714 |
| Cl2 | 6,579 | 56,22 | C2H6 | 5,562 | 63,80 |
| CO | 1,505 | 39,85 | C3H8 | 8,779 | 84,45 |
| CO2 | 3,640 | 42,67 | C6H6 | 18,24 | 115,4 |
Уравнение (1.6) можно переписать так, чтобы выразить в явном виде давление
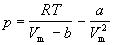
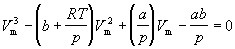
Уравнение (1.8) содержит объем в третьей степени и, следовательно, имеет или три действительных корня, или один действительный и два мнимых. При высоких температурах уравнение (1.8) имеет один действительный корень, и по мере повышения температуры кривые, вычисленные по уравнению Ван-дер-Ваальса, приближаются к гиперболам, соответствующим уравнению состояния идеального газа.
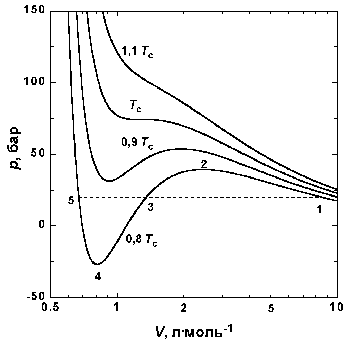 |
| Рис.1.4 Изотермы Ван-дер-Ваальса для СО2 |
На рис. 1.4 (стр. 7) приведены изотермы, вычисленные по уравнению Ван-дер-Ваальса для диоксида углерода (значения констант a и b взяты из табл. 1.3). Из рисунка видно, что при температурах ниже критической (31,04 °С) вместо горизонтальных прямых, соответствующих равновесию жидкости и пара, получаются волнообразные кривые 12345 с тремя действительными корнями, из которых только два, 1 и 5, физически осуществимы. Третий корень (точка 3) физически не реален, поскольку находится на участке кривой 234, противоречащем условию стабильности термодинамической системы 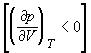
Согласно правилу Максвелла (the Maxwell construction), которое имеет теоретическое обоснование, для того, чтобы расчетная кривая соответствовала экспериментальной равновесной изотерме, нужно вместо кривой 12345 провести горизонтальную прямую 15 так, чтобы площади 1231 и 3453 были равны. Тогда ордината прямой 15 будет равна давлению насыщенного пара, а абсциссы точек 1 и 5 – мольным объемам пара и жидкости при данной температуре.
По мере повышения температуры все три корня сближаются, и при критической температуре Tc все три корня становятся равными. В критической точке изотерма Ван-дер-Ваальса имеет точку перегиба [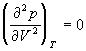
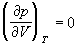
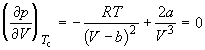
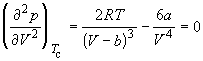
Совместное решение этих уравнений дает:
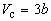
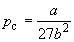
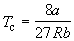
что позволяет определять константы уравнения Ван-дер-Ваальса из критических параметров газа. Соответственно, согласно уравнению Ван-дер-Ваальса, критический фактор сжимаемости Zc для всех газов должен быть равен
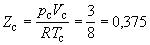
Из таблицы 1.2 видно, что хотя значение Zc для реальных газов приблизительно постоянно (0,27 – 0,30 для неполярных молекул), оно все же заметно меньше вытекающего из уравнения Ван-дер-Ваальса. Для полярных молекул наблюдается еще большее расхождение.
Принципиальное значение уравнения Ван-дер-Ваальса определяется следующими обстоятельствами:
1) уравнение было получено из модельных представлений о свойствах реальных газов и жидкостей, а не явилось результатом эмпирического подбора функции f(p,V,T), описывающей свойства реальных газов;
2) уравнение долго рассматривалось как некоторый общий вид уравнения состояния реальных газов, на основе которого было построено много других уравнений состояния (см. ниже);
3) с помощью уравнения Ван-дер-Ваальса впервые удалось описать явление перехода газа в жидкость и проанализировать критические явления. В этом отношении уравнение Ван-дер-Ваальса имеет преимущество даже перед более точными уравнениями в вириальной форме (см. 1.1, 1.2).
Причиной недостаточной точности уравнения Ван-дер-Ваальс считал ассоциацию молекул в газовой фазе, которую не удается описать, учитывая зависимость параметров a и b от объема и температуры, без использования дополнительных постоянных. После 1873 г. сам Ван-дер-Ваальс предложил еще шесть вариантов своего уравнения, последнее из которых относится к 1911 г. и содержит пять эмпирических постоянных. Две модификации уравнения (1.5) предложил Клаузиус, и обе они связаны с усложнением вида постоянной b. Больцман получил три уравнения этого типа, изменяя выражения для постоянной a. Всего известно более сотни подобных уравнений, отличающихся числом эмпирических постоянных, степенью точности и областью применимости. Выяснилось, что ни одно из уравнений состояния, содержащих менее 5 индивидуальных постоянных, не оказалось достаточно точным для описания реальных газов в широком диапазоне p, V, T, и все эти уравнения оказались непригодными в области конденсации газов. Из простых уравнений с двумя индивидуальными параметрами неплохие результаты дают уравнения Дитеричи и Бертло (см. табл. 1.4).


Сервер создается при поддержке Российского фонда фундаментальных исследований
Не разрешается копирование материалов и размещение на других Web-сайтах
Вебдизайн: Copyright (C) И. Миняйлова и В. Миняйлов
Copyright (C) Химический факультет МГУ
Написать письмо редактору
🔍 Видео
Урок 194. Уравнение Ван-дер-ВаальсаСкачать

Лекция №7 "Уравнение Ван-дер-Ваальса. Гидродинамика" (Булыгин В.С.)Скачать

Уравнение Ван-дер-Ваальса (вывод и применение). By Bogatov N.A.Скачать

Реальный газ Уравнение Ван-Дер-ВаальсаСкачать

Реальные газы. Изотермы Эндрюса и Ван-Дер-Ваальса. Метастабильные состоянияСкачать

Классы усилителей: A, B, C, D... Остальные ГСкачать

Галилео. Эксперимент. Межмолекулярное взаимодействие свинцаСкачать

Сила КориолисаСкачать

Лекция №7 "Газ Ван-дер-Ваальса. Эффект Джоуля-Томсона" (Овчинкин В.А.)Скачать

270. Силы Ван-дер-ВаальсаСкачать

Уравнение Ван дер Ваальса. Часть 3. Внутренняя энергия реального газа. Фазовые переходы 1 рода.Скачать

Урок 156. Уравнение состояния идеального газа. Квазистатические процессыСкачать

Лекция №6 "Фазовые переходы. Газ Ван-дер-Ваальса"Скачать

Физический кружок: реальные газы, фазовое равновесие | Шестое занятиеСкачать

Урок 195. Изотермы реального газаСкачать

Статистическая физика №12. Часть 1. Слабонеидеальные газы. Газ Ван-дер-Ваальса.Скачать

Термодинамика Л10. 2023. Уравнение Ван-дер-ВаальсаСкачать

Силы Ван-дер-Ваальса (видео 1) | Силы межмолекулярного взаимодействия | ХимияСкачать

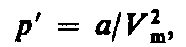 где а — постоянная Ван-дер-Ваальса, характеризующая силы межмолекулярного притяжения, Vm — молярный объем
где а — постоянная Ван-дер-Ваальса, характеризующая силы межмолекулярного притяжения, Vm — молярный объем