Все электромагнитные процессы макроскопической электродинамики подчиняются уравнениям Максвелла, сформулированным в 1873 г. в виде дифференциальных уравнений. Эти уравнения связывают воедино электрические и магнитные характеристики поля:
rot H = Iпр + 

rot Е = — 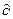

div D = 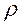
Физический смысл этих уравнений заключается в следующем.
Первое уравнение Максвелла(5.9,а) является обобщенным законом Ампера (закон полного тока) и говорит о том, что если в некоторой точке пространства существует переменное электрическое поле Е, создающее токи проводимости Iпр = σE и токи смещения Iсм = iω 
Второе уравнение Максвелла (5.9,б) является обобщенным законом магнитной индукции Фарадея. Фарадей установил, что если замкнутый контур пронизывается переменным магнитным потоком Ф, то в контуре возникает электродвижущая сила (ЭДС) равная скорости изменения магнитного потока:
е = — 

Знак «минус» в правой части означает, что возникающая в контуре ЭДС стремится воспрепятствовать изменению потока, пронизывающего контур.
Физический смысл второго уравнения Максвелла заключается в том, что всякое изменение магнитного поля во времени непрерывно вызывает независимо от параметров среды появление электрического поля.
Второе уравнение Максвелла связано с гармоническим колебанием соотношением:
rot Е = — 

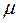
т.е. оно утверждает, что если в некоторой точке пространства существует переменное магнитное поле, то в окрестностях этой точки возникает переменное вихревое электрическое поле. Магнитное поле и создаваемое им электрическое поле образуют левовинтовую систему.
Следует отметить, что электрическое поле может быть как вихревым, так и потенциальным. Источником потенциального электрического поля являются заряды (в случае электрических полей), которые находятся в тех точках пространства, где текут токи проводимости, представляющие собой движущиеся заряды.
Таким образом, гармоническое электрическое поле может быть вихревым, потенциальным или представлять суперпозицию (сумму) потенциального и вихревого полей, тогда как магнитное поле только вихревое.
Первое и второе уравнения Максвелла говорят о том, что между электрической и магнитной составляющими в переменном электромагнитном поле существует тесная взаимосвязь, которая выражается тем, что созданное сторонними источниками меняющееся во времени электромагнитное поле, может существовать вне этого источника за счет собственной энергии, перекачивающейся из энергии электрического поля в энергию магнитного поля и обратно.
Третье уравнение Максвелла(материальное уравнение 5.9,в) — это обобщенный закон Гаусса для случая переменных процессов, физически означает, что источником электрического поля являются электрические заряды, т.е. электрическая индукция D связана с плотностью электрических зарядов 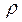
Четвертое уравнениеМаксвелла (материальное уравнение 5.9,г) показывает, что в природе отсутствуют магнитные заряды, а линии вектора В непрерывны и всегда пронизывают любую замкнутую поверхность.
Таким образом, третье и четвертое уравнения Максвелла учитывают электрическую и магнитную характеристики среды. Действительно, в случае линейных изотропных сред можно записать:
D = 
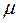
Следует отметить, что к основным уравнениям электродинамики относят и закон Ома в дифференциальной форме (5.6), который выражает зависимость плотности тока Iпр в какой-либо точке проводящей сферы от напряженности электрического поля в этой точке.
Таким образом, мы рассмотрели основные уравнения электродинамики, каждое из которых описывает те или иные свойства электромагнитного поля. Однако, для полного анализа электродинамических процессов необходимо использовать полную систему уравнений Максвелла, содержащую основные уравнения Максвелла (5.9,а-г) и материальные уравнения (5.6) и (5.10), которая записывается в виде:
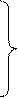



rot Е = — 

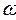
div D = 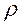
D = 
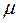
Поскольку уравнения (5.13) и (5.14) являются линейными дифференциальными уравнениями, можно утверждать, что электромагнитные поля удовлетворяют принципу суперпозиции.
- Уравнения Максвелла
- Значение уравнений Максвелла
- Система уравнений Максвелла
- Готовые работы на аналогичную тему
- Физический смысл уравнений Максвелла
- Границы применимости уравнений Максвелла
- Физический смысл ii уравнения максвелла
- Уравнения и история
- Следствия из уравнений Максвелла
- Решения уравнений Максвелла
- Компьютерные программы моделирования электромагнитных полей
- Заключение
- 🎥 Видео
Видео:О чем говорят уравнения Максвелла? Видео 1/2Скачать

Уравнения Максвелла
Вы будете перенаправлены на Автор24
Видео:ЧК_МИФ: 4.1.1.ДФ_1 Физический смысл уравнений МаксвеллаСкачать

Значение уравнений Максвелла
Уравнения Дж. Максвелла создают основу для предложенной им теории электромагнитных явлений, которая объяснила все известные в то время эмпирические факты, некоторые эффекты предсказала. Главным выводом теории Максвелла стало положение о существовании электромагнитных волн, которые распространяются со скоростью света.
Уравнения, предложенные Максвеллом, в электромагнетизме играют роль подобную роли законов Ньютона в классической механике. Они явились обобщением экспериментальных законов и продолжением идей ученых (Кулона, Ампера, Фарадея и др.) изучавших электромагнетизм до Максвелла.
Сам Максвелл предложил двадцать уравнений в дифференциальной форме с двадцатью неизвестными величинами. В современном виде мы имеем систему уравнений Максвелла благодаря немецкому физику Г. Герцу и англичанину О. Хэвисайду. С помощью этих уравнений можно описать все электромагнитные явления.
Видео:Билеты №32, 33 "Уравнения Максвелла"Скачать

Система уравнений Максвелла
Систему уравнений Максвелла составляют:
Выражения (1)-(4) называют полевыми уравнениями, они применимы для описания всех макроскопических электромагнитных явлений. Иногда уравнения системы Максвелла группируют в пары, первую пару составляют из второго и третьего уравнения, вторую пару — из первого и четвертого уравнений. При этом говорят, что в первую пару уравнений входят только основные характеристики поля ($overrightarrow и overrightarrow$), а во вторую пару — вспомогательные ($overrightarrow и overrightarrow$).
Каждое из векторных уравнений (1) и (2) эквивалентно трем скалярным уравнениям. Эти уравнения связывают компоненты векторов, которые находятся в левой и правой частях выражений. Так, в скалярном виде уравнение (1) представляется как:
Готовые работы на аналогичную тему
В скалярном виде уравнение (2) запишем как:
Третье уравнение из системы Максвелла в скалярном виде:
Четвертое уравнение в скалярной форме примет следующий вид:
Для того чтобы рассмотреть конкретную ситуацию, систему уравнений (1)-(4) дополняют следующими материальными уравнениями, которые учитывают электромагнитные свойства среды:
Необходимо отметить, что существует целый ряд явлений, в которых материальные уравнения существенно отличны от уравнений (5), например, если речь идет о нелинейных явлениях. В таких случаях получение материальных уравнений составляет отдельную научную задачу.
Видео:ЧК_МИФ /ЛИКБЕЗ/ 3_3_5_1 СИСТЕМА УРАВНЕНИЙ МАКСВЕЛЛА. ПРИМЕРЫ (минимум теории)Скачать

Физический смысл уравнений Максвелла
Уравнение (1) системы указывает на то, что двумя возможными источниками магнитного поля являются токи проводимости ($overrightarrow$) и токи смещения ($frac<partial overrightarrow>$).
Уравнение (2) является законом электромагнитной индукции и отображает тот факт, что переменное магнитное поле — один из источников возникновения электрического поля.
Следующим источником электрического поля служат электрические заряды, что и отображает уравнение (4), которое является, по сути, законом Кулона.
Уравнение (3) означает, что линии магнитной индукции не имеют источников (они либо замкнуты, либо уходят в бесконечность), что приводит к выводу об отсутствии магнитных зарядов, которые создают магнитное поле.
Материальные уравнения (5) — это соотношения между векторами поля и токами. Диэлектрические свойства среды заключены в диэлектрической проницаемости ($varepsilon $). Магнитные свойства, которые описывает намагниченность, учтены в магнитной проницаемости ($mu $). Проводящие свойства среды сосредоточены в удельной проводимости ($sigma $).
Уравнения поля линейны и учитывают принцип суперпозиции.
Видео:Физика. Лекция 8. Уравнения Максвелла и электромагнитные волны.Скачать

Границы применимости уравнений Максвелла
Система уравнений Максвелла ограничена следующими условиями:
Материальные тела должны быть неподвижны в поле.
Постоянные $varepsilon , mu ,sigma $ могут зависеть от координат, но не должны зависеть от времени и векторов поля.
В поле не должно находиться постоянных магнитов и ферромагнитных тел.
Если существует необходимость учета движения среды, то уравнения системы Максвелла оставляют неизменными, а движение учитывается в материальных уравнениях, которые становятся зависимыми от скорости среды и существенно усложняются. Кроме прочего материальные уравнения перестают быть соотношениями между парами величин, как в (5). Например, плотность тока проводимости становится зависимой от индукции магнитного поля, а не только от напряженности электрического поля.
Магнитное поле постоянных магнитов, например, можно описать, используя систему Максвелла, если известна намагниченность. Но, если заданы токи, то в присутствии ферромагнетиков описать поле при помощи данных уравнений не получится.
Задание: Докажите, что из уравнений Максвелла следует закон сохранения заряда.
Решение:
В качестве основания для решения задачи используем из системы Максвелла уравнение:
Проведем операцию дивергирования в обеих частях выражения (1.1):
Для выражения (1.2) в соответствии с теоремой равенстве нулю дивергенции ротора имеем:
Рассмотрим второе слагаемое в правой части. Мы можем поменять порядок дифференцирования, так как время и пространственные координаты независимы, то есть записать:
В соответствии с системой Максвелла мы знаем, что источниками электрических полей служат заряды или:
Что позволяет нам записать уравнение (1.4) в виде:
Что дает нам закон сохранения заряда, который записан в виде:
Данное уравнение называют уравнением непрерывности тока, оно содержит в себе закон сохранения заряда, что совершенно очевидно, если выражение (1.8), записать в интегральной форме:
тогда если области замкнуты и изолированы получаем:
Что требовалось доказать.
Задание: Покажите, что уравнения $rotoverrightarrow=-frac<partial overrightarrow>$ и $divoverrightarrow=0$ , входящие в систему Максвелла не противоречат друг другу.
Решение:
За основу решения примем уравнение:
Возьмём дивергенцию от обеих частей уравнения:
В соответствии с теоремой равенстве нулю дивергенции ротора имеем:
Соответственно, получаем, что
Выражение $divoverrightarrow=const$ не противоречит тому, что $divoverrightarrow=0$.
Мы получили, что уравнения $rotoverrightarrow=-frac<partial overrightarrow>$ и $divoverrightarrow=0$ совместны, что требовалось показать.
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата последнего обновления статьи: 01 03 2021
Видео:Лекция №9. Уравнения МаксвеллаСкачать

Физический смысл ii уравнения максвелла
Уравнения Джеймса Максвелла (1873 г) описывают любые электромагнитные поля. Но этим их значение не исчерпывается.
Они были одной из отправных точек при создании общей теории относительности Альберта Эйнштейна (отчасти от них попала в формулы теории относительности скорость света). Эйнштейн писал: «Со времени обоснования теоретической физики Ньютоном наибольшее изменение в ее теоретических основах, другими словами, в нашем представлении о структуре реальности, было достигнуто благодаря исследованиям электромагнитных явлений Фарадеем и Максвеллом».
Из-за уравнений Максвелла были открыты радиоволны. Да, именно так: Максвелл создал систему своих уравнений до обнаружения радиоволн. Немало физиков того времени выступили против теории Максвелла (много было недовольных током смещения). Герман фон Гельмгольц придумал свою теорию и поручил экспериментально проверить её своему ученику Генриху Герцу (вообще-то его звали Хайнрих Хертц, но в русскую транскрипцию попало и устоялось неправильное прочтение). Но опыты Герца показали, что Максвелл прав. И Герц вошел в историю как первооткрыватель радиоволн.
Уравнения Максвелла вошли и в квантовую механику, положив начало квантовой электродинамике.
До сих пор нет ни одного факта, ставящего под сомнение уравнения Максвелла. Причем, не только в мире привычных для нас размеров и скоростей, но и в квантовой механике и в теории относительности. Это очень важно. Ведь не секрет, что квантовая механика и теория относительности плохо стыкуются друг с другом. И физики современности прилагают большие усилия, чтобы свести их воедино в общую теорию (теории струн, суперсимметрии, суперструн и т.д.), но пока это не очень получается. А уравнения Максвелла работают и в квантовом микромире и в теории относительности, связывая наши представления о мире.
Казалось бы, при такой значимости понимать уравнения Максвелла должен любой человек, считающий себя образованным. Во всяком случае, тот, кто как-то связан с электромагнитными полями. Но, к сожалению, уравнения Максвелла даже среди профессионалов мало кто знает, а понимает еще меньше.
Почему-то многие при виде уравнений Максвелла впадают в благоговейный ступор, полагая, что без знания высшей математики там делать нечего. Это не так. Для понимания физической сути уравнений Максвелла хватит школьного образования.
Такое понимание необходимо, если вы хотите что-то (например, антенну) придумать или понять сами. Или не хотите быть обманутым очередным «гениальным изобретателем-ниспровергателем» (а таковых в последнее время, увы, развелось немало).
Уравнения и история
1. Первое уравнение Максвелла представляет собой закон Гаусса (да, того самого Карла Гаусса, чьё имя носит колоколообразное распределение случайных величин; в те времена можно было быть и выдающимся математиком и выдающимся физиком одновременно) для электрических полей. Максвелл записал его в дифференциальной форме. В современной записи оно выглядит так (не пугайтесь математики, и не бросайте чтение хотя бы еще несколько абзацев) :
E – векторное электрическое поле (здесь и далее жирным шрифтом выделены векторные величины, а курсивом — скалярные);
∇· – значок оператора дивергенции (потока);
εo = 8,85418782. •10 -12 Ф/м – диэлектрическая постоянная вакуума, измеряется экспериментально по силе притяжения между зарядами.
Первое уравнение говорит об очевидной вещи…
Но перед тем как ее озвучить, давайте разберемся, что такое дивергенция векторной величины. Вы видели водопроводный кран? Ну, тогда вы хорошо знаете, что такое дивергенция. В переводе с латинского это извержение наружу. Иначе говоря, поток. Для водопроводного крана это поток вытекающей воды, который тем больше, чем больше диаметр трубы и напор воды в ней. Если дивергенция больше нуля, то точка является источником, если меньше – стоком. Теперь вы знаете половину нужной векторной математики.
…Но вернемся к первому уравнению Максвелла (оно же – закон Гаусса). Оно говорит том, что поток электрического поля Е через любую замкнутую поверхность зависит от суммарного электрического заряда внутри этой поверхности. Иначе говоря, если из замкнутого бассейна вытекает воды больше, чем в него втекает (то есть суммарный поток из бассейна получается больше нуля), то ясно, что внутри бассейна прячется труба – источник этой самой воды (иначе бы она быстро кончилась).
С электрическим полем то же самое: если есть электрический заряд (труба-источник воды в бассейне), то поле от него будет вытекать наружу во все стороны (вода будет выливаться через края).
3. Третье (нарушим порядок следования для удобства понимания) уравнение Максвелла – это тоже закон Гаусса, записанный в дифференциальной форме. Но для магнитных полей:
B – векторное магнитное поле.
Это уравнение говорит о том, что поток магнитного поля через любую замкнутую поверхность всегда равен нулю. Или, иначе говоря, что одиночных магнитных зарядов в природе не существует. Вот электрически отрицательный электрон и положительный электрически протон есть и могут успешно существовать отдельно друг от друга. А полюса магнита отдельными не бывают. Только вместе. Один такой полюс толкает вперед, другой – тянет назад.
В примере с бассейном это две трубы, разнесенные на какое-то расстояние: сколько по одной втекает, столько по другой и вытекает. Движение воды по кругу у нас есть. Но суммарный поток равен нулю: сколько пришло, столько и ушло. Наружу ничего не вытекает. Точно также как и в потоке магнитного поля через замкнутую поверхность.
2. Второе уравнение Максвелла это закон Фарадея (на всех конденсаторах написано имя Майкла Фарадея) впервые в дифференциальной форме записан Максвеллом в качестве его третьего уравнения:
∇× – значок оператора ротора (вихря);
∂B/∂t – частная производная (изменение) B по времени. Частная в том смысле, что магнитное поле вообще меняется и в пространстве и во времени, но тут нас интересует только его изменение во времени.
Это уравнение говорит, что ротор (интеграл по замкнутому контуру) электрического поля Е равен потоку (т.е. скорости изменения во времени) магнитного поля В сквозь этот контур.
… Тут надо остановиться и разобраться, что такое ротор векторного поля. Вы наблюдали, как вода уходит из ванной в сливное отверстие? Тогда вы этот самый ротор видели: крутящаяся воронка воды вокруг открытой пробки и есть ротор. Точнее говоря, не сама воронка, а сумма (еще точнее –интеграл: ведь любой интеграл это сумма чего-то) векторов угловых скоростей, частиц воды, крутящихся по замкнутому контуру вокруг отверстия пробки. Всё, теперь вы знаете векторную математику на уровне, достаточном для полного понимания Максвелла…
Но вернемся со второму уравнению Максвелла. Там то же самое, что и в ванне: чем больше и чем быстрее изменяется магнитное поле внутри контура (чем сильнее сосёт воду сливное отверстие), тем сильнее раскручивается вихревое электрическое поле (стекающая вода) вокруг этого контура (отверстия).
На законе Фарадея (т.е. на втором уравнении Максвелла) работают все генераторы электричества: механически вращающийся магнит создает изменяющееся магнитное поле внутри катушки, с которой снимается индуцированный электрический ток.
4. Четвертое уравнение Максвелла. Сначала Максвелл взял закон Андре Ампера (которого он называл «Ньютоном электричества», а мы вспоминаем при каждом измерении тока), связывающий постоянный ток и магнитное поле вокруг него:
с – скорость света (на самом деле мы тут забегаем вперед, говоря, что это скорость света. Ни Ампер, ни Максвелл, когда писали свои уравнения этого еще не знали, и называли с 2 «электромагнитной постоянной»).
Этот закон говорит, что ротор магнитного поля (интеграл от B по замкнутому контуру) равен току, текущему сквозь этот контур. Ну не прямо равен, а с коэффициентом 1/εoc 2 . Иногда этот коэффициент обозначают как μo и называют магнитной постоянной вакуума. Но это делают только для упрощения записи: μo = 1/εoc 2 .
Проще говоря, закон Ампера говорит, что вокруг провода с током возникает кольцевое (ротор же) магнитное поле (школьный опыт с компасом и проводником с током помните?)
Итак, Максвелл собрал все известные на тот момент законы электричества и магнетизма и записал их в виде дифференциальных уравнений.
…Историческое отступление. Максвелл не использовал векторных обозначений и записывал свои уравнения в громоздком компонентном (по трем осям) виде (поэтому у него получилась система из 20-ти скалярных уравнений и с 20-ю же неизвестными). Понятия и символы дивергенции и ротора тогда еще не были придуманы. Кстати, в основном благодаря Максвеллу, стала очевидной важность создания таких комбинаций производных, которые мы сегодня называем ротором и дивергенцией. Эту работу проделали Оливер Хевисайд (который первый применил комплексные числа для анализа электрических цепей), Хайнрих Хертц (ну ладно, пусть он будет Генрих Герц, хотя Хайнрих бы не понял, что это его имя) и Джозайя Гиббс (один из создателей векторного анализа). Они переписали систему уравнений Максвелла в современном виде, упростив ее до 4-х векторных уравнений (против 20-ти скалярных у Максвелла). То есть Максвеллу было намного труднее управляться и анализировать написанные им уравнения. Но он справился…
Первые три (будем считать по современной векторной форме записи, хотя у Максвелла это было не 3, а 15) уравнения (два закона Гаусса и один Фарадея) проблем не обнаружили и были оставлены Максвеллом без изменений (он только переписал их в дифференциальном виде).
А вот в законе Ампера Максвелл заметил странность (и с этого момента начался его путь к современной электродинамике).
Дело в том, что если от закона Ампера взять дивергенцию от обеих частей уравнения, то левая его часть обратится в ноль (математически говоря, дивергенция ротора всегда равна нулю; а если на пальцах: ротор крутится, но наружу из него ничего не вытекает, поэтому поток-дивергенция у ротора отсутствует). Тогда из математики получается, что и правая часть уравнения обязана быть нулевой. А в правой части получается дивергенция (поток) тока, т.е. полный ток через замкнутую поверхность. Но физически очевидно, что такой ток вовсе не обязан быть равным нулю. Ведь ток – это движение зарядов, а они вполне двигаются из одного места в другое.
Получается нестыковка: физика говорит, что ток есть (вставьте внутрь поверхности любой переменный источник зарядов и ток точно будет), а математика говорит, что его быть не может. Следовательно, виновата математика.
Значит, что закон Ампера верен для статичного поля, но не выполняется для изменяющихся полей (операция дивергенции-потока, которую мы вслед за Максвеллом неудачно попытались провести над законом Ампера и есть изменение во времени).
Максвелл заметил это несоответствие, и чтобы избежать его предложил в закон Ампера добавить к току дополнительный член (1/c 2 )·∂E/∂t. Получилось четвертое уравнение Максвелла, называемое теоремой о циркуляции магнитного поля:
Это уравнение отличается от закона Ампера только добавкой (1/c 2 )·∂E/∂t. Добавка эта сделана к току. Следовательно, она описывает какой-то ток. Максвелл назвал его током смещения.
Четвертое уравнение Максвелла говорит о том, что вихревое магнитное поле может быть порождено как током в проводнике, так и изменением электрического поля. Причем, в смысле порождения магнитного поля ток в проводнике ничем не отличается от изменения электрического поля Е в диэлектрике. Поэтому изменение Е во времени называют током смещения.
Ток смещения (добавка Максвелла в 4-е уравнение) бывает только в диэлектрике (просто потому, что в хорошем проводнике электрическое поле отсутствует, а значит и меняться не может). А ток проводимости (правая часть закона Ампера) – только в проводнике (в диэлектрике отсутствуют заряды, способные двигаться, а движение зарядов — это и есть ток проводимости).
Допустим, мы длинными прямыми проводами подключили к генератору переменного тока простейший воздушный конденсатор, состоящий из двух пластин. Понятно, в цепи потечет какой-то ток. Возьмем маленький индикатор переменного магнитного поля и поведем его вдоль провода. Индикатор покажет некую величину магнитного поля: ток проводимости ведь по проводу течет, значит, он обязан создавать вокруг себя магнитное поле.
А теперь, продолжая вести индикатор вдоль проводов, передвинем его дальше, так чтобы он оказался бы напротив, конденсатора (сбоку от пластин). Что покажет индикатор? Ноль (ведь тока проводимости между обкладками конденсатора нет)? Это было бы нелогично: одинаковое магнитное поле вдоль провода, потом вдруг полный ноль между обкладками, а потом (когда пойдем индикатором вдоль второго провода) – снова поле. Интуитивно ясно, что магнитное поле вдоль всей цепи должно быть одинаковым (считая размеры конструкции малыми, чтобы пренебречь излучением).
Так и есть на практике. Но магнитное поле около конденсатора создает не ток, а меняющее по времени электрическое поле между его обкладками, которое Максвелл назвал током смещения.
Именно это и описывает дополнительный член в 4-м уравнении Максвелла. А его величина выбрана так, чтобы в ситуации данного примера магнитное поле везде (и около провода, около конденсатора) получалось бы одинаковым.
Следствия из уравнений Максвелла
Может сложиться впечатление, что добавка (1/c 2 )·∂E/∂t в четвертое уравнение Максвелла – это лишь небольшая математическая коррекция закона Ампера, чтобы на переменных полях из уравнения получать то, что имеем из физики.
Да, пока мы рассматриваем только одно четвертое уравнение, ничего особенно интересного не появляется (кроме того факта, что переменное электрическое поле порождает вокруг себя магнитное поле точно так же, как и электрический ток в проводе).
Но если рассмотреть всю систему уравнений Максвелла целиком, то оказывается, что эта небольшая добавка в 4-е уравнение приносит много важного.
1. Из совместного изучения второго и четвертого уравнений (точнее, добавки к 4-му уравнению) Максвелла следует, что электромагнитное поле сохраняет само себя и не может исчезнуть.
Допустим, мы имеем магнитное поле, а затем выключаем его. То есть, меняем его скачком. По закону Фарадея за счет изменения магнитного поля вокруг него (то есть чуть дальше) появляется электрическое поле. Причем тоже изменяющееся (т.к. его прародитель – магнитное поле было изменяющимся). По добавке Максвелла в 4-е уравнение это электрическое поле создаст вокруг себя (то есть еще дальше от исходного) новое магнитное поле (также изменяющееся). И так до бесконечности: магнитное и электрическое поле, перекачиваясь одно в другое, распространяются в пространстве до бесконечности. Узнали в этом описании радиоволну?
2. Из системы уравнений Максвелла вытекает, что распространяющееся в пространстве электромагнитное поле может делать это только со скоростью света с (давайте я опущу математический вывод этого факта, а то читатель еще наверное не пришел в себя от роторов и дивергенций).
Этот факт произвел революцию в физике. Ведь когда Максвелл писал свои уравнения, еще не было известно, что коэффициент с – это скорость света (мы её сразу назвали так, потому что знали ответ, но Максвелл-то его вначале не знал). Тогда это была просто некая константа. Точнее говоря, «электромагнитной константой» называли величину с 2 , получая её из экспериментов со светом никак не связанных.
… Отступление о том, как измеряли эту самую «электромагнитную константу». Измеряя силу притяжения между двумя единичными (причём, неважно, что считать единицей, их величина потом сокращается в дроби) зарядами можно экспериментально получить электрическую постоянную вакуума εo = 8,85418782. •10 -12 Ф/м. Магнитную постоянную вакуума μo = 1/εoc 2 из закона Ампера можно экспериментально определить, измеряя силы притяжения между двумя единичными токами (движение тех же единичных зарядов). Она равна μo = 1,25663706. •10 -6 Гн/м. Взяв обратную величину от произведения этих величин, получим c 2 = 1/εoμo «электромагнитную постоянную».
Таким образом, прямо из экспериментов с зарядами и токами нашли значение константы c 2 . А из уравнений Максвелла оказалось, что электромагнитное поле обязано распространяться со скоростью c. Когда Максвелл впервые проделал это вычисление по своим уравнениям, оказалось что полученная цифра (
3·10 8 м/с) очень близка к скорости света (эту скорость астрономы измерили до Максвелла по запаздыванию затмений спутников Юпитера).
Максвелл отметил это совпадение: «Мы едва ли можем избежать заключения, что свет это волнообразное движение той же самой среды, которая вызывает электрические и магнитные явления». Это революционное обобщение. До Максвелла свет рассматривался как область физики, совершенно отдельная от электричества и магнетизма. После Максвелла свет стал электромагнитными колебаниями и появились электромагнитные волны.
. Отступление о цифрах. Взяв квадратный корень из 1/εoμo получим точную скорость света c = 2,99792458·10 8 м/с. Кстати, это абсолютно точное значение. В отличие от других физических констант, которые имеют бесконечный хвост цифр за запятой, скорость света равна точно 299 792 458 м/с. Фокус тут не в какой-то сверхъестественной точности измерений, а том, что с 1983 года 1 метр в международной системе единиц (СИ) определён, как расстояние, которое проходит свет в вакууме за промежуток времени, равный 1/299792458 секунды. То есть человечество подогнало свой метр под физическую константу c.
Квадратный корень из отношения μo/εo дает волновое сопротивление вакуума W = 376,730031 Ом. Возникает большой соблазн записать эту цифру как 120π, но увы это не точно: 120π = 376,991184. Так что число π (которое имеет бесконечное число цифр после запятой) не связано напрямую с электромагнетизмом.
Решения уравнений Максвелла
Решать мы их не будем. Это сложно. Тем более что решения зависят от начальных и граничных условий (расположения в пространстве токов и зарядов, поверхностей). Поэтому решать уравнения Максвелла надо заново для каждой задачи (например, расчета конкретной антенны в заданном окружении). И занимаются этим, в основном моделирующие компьютерные программы.
Здесь мы рассмотрим только готовое решение для электромагнитной волны в свободном пространстве.
Из этого решения вытекает положение векторов электрического и магнитного поля относительно направления движения электромагнитной волны:
- В перпендикулярно направлению распространения.
- E также перпендикулярно направлению распространения.
- В и Е перпендикулярны между собой.
В нашем трехмерном мире это возможно, только если B, Е и направление движения волны расположены по трем координатным осям. На следующей анимации показана электромагнитная волна в свободном пространстве:
Являющееся решением системы уравнений Максвелла трехмерное волновое уравнение по E для свободного пространства выглядит так:
Это очень интересное уравнение.
Во-первых, в нём явно видна равнозначность между пространственными координатами и временем: x, y, z и t стоят в одном ряду и в одном и том же виде (множитель c 2 перед временем говорит лишь о том, что у координат и времени разная размерность и этот множитель лишь приводит ее к одной: скорость умножить на время получаются метры). И эта идентичность расположения x, y, z и t говорит о том, что для электромагнитной волны наш мир четырехмерен, время является точно такой же полноправной координатой, как и x, y, z.
Во-вторых, в трехмерном волновом уравнении x, y, z и t стоят в квадрате. Что говорит от четырехмерной симметрии нашего мира (квадрат величины не зависит от ее знака: плюс или минус). Поэтому знаки координат x, y, z, и знак времени t можно менять на противоположные без изменения уравнения.
Решением этого трехмерного волнового уравнения является любая функция (волна), движущаяся в пространстве со скоростью c. Но из-за того, что в этом уравнении c встречается только в виде квадрата, изменение знака скорости c на противоположный ничего не меняет. Поэтому общим математическим решением волнового уравнения является сумма (наложение) двух волн со скоростью света одновременно бегущих в противоположные стороны.
И тут мы делаем следующий шаг: утверждаем (без математического доказательства, просто из опыта), что электромагнитные волны, создаваемые источником, всегда бегут только от него. Согласитесь, с точки зрения здравого смысла было бы очень странно, если бы еще до включения источника некая волна зародилась где-то очень далеко и успела бы прибыть к источнику именно в тот момент, когда мы надумали его включить. Решение уравнений Максвелла дает обеим волнам равные права. И мы сами на опыте устанавливаем добавочное (отсутствующее в уравнениях Максвелла) правило, что физический смысл имеет только одна из этих волн. Та, которая уходит от источника.
Из-за этого добавочного правила мы теряем симметрию по времени, которая есть в уравнениях Максвелла.
Кстати говоря, математиками внимательно исследовалась такая электродинамика, которая обходится без этого дополнительного правила и имеет две волны. Как ни странно, результаты таких исследований во многих случаях не являются физически абсурдными (а иногда они имеют явный физический смысл, например, прямая и обратная волна в длинных линиях). Но в физическую гипотезу такая электродинамика так и не превратилась, оставшись математическим экспериментом. Хотя возможность обратного движения по времени (т.е. его симметрии) так привлекательна, но… Так что мы пользуемся электродинамикой, в которой пространство симметрично, а время – нет (то есть волны всегда уходят от источника).
Компьютерные программы моделирования электромагнитных полей
Если источник точечный (бесконечно малый), то понятно, что волны, расходящиеся от него, в свободном пространстве будут сферическими. То есть одинаковыми по всем трем пространственным координатам. В таких условиях решение трехмерного волнового уравнения получается довольно простым: поле убывает обратно пропорционально расстоянию.
Но точечных источников не бывает. Реально они все протяженные. Как быть? Это просто: представим протяженный источник как сумму большого числа точечных источников (а для каждого из них мы поле считать уже умеем). А потом просуммируем все поля от всех точечных источников. Точнее проинтегрируем (интеграл это ведь сумма) по всему объему.
Получим два интегральных уравнения: интегральное уравнение электрического поля: electric-field integral equation (EFIE) и интегральное уравнение магнитного поля magnetic Field Integral Equation (MFIE).
Исходными данными для этих уравнений является геометрия рассчитываемого источника поля (антенны, например) и распределение токов в пространстве.
Два свойства EFIE делают его незаменимым для расчета антенн:
EFIE позволяет решать задачи излучения и рассеяния в неограниченной области (граница которой находится в бесконечности). Иными словами: можно рассчитывать излучающую антенну (ее поле и уходит в бесконечность).
EFIE может быть решено численными методами, в частности, методом моментов.
Для расчета полей в ограниченной области (например резонатор, волновод, и т.п.) лучше подходит MFIE.
Компьютерные программы моделирования антенн (например, MMANA-GAL, GAL-ANA) работают, решая уравнение электрического поля EFIE для каждой конкретной антенны.
Заключение
Вот система уравнений Максвелла во всей красе:
| ∇·E = ρ/εo | Закон Гаусса для E |
| ∇×E = – ∂B/∂t | Закон Фарадея |
| ∇·B = 0 | Закон Гаусса для В |
| ∇×B = j/εoc 2 + (1/c 2 )·∂E/∂t | Теорема о циркуляции В |
Она описывает абсолютно все электромагнитные явления. И вы ее теперь понимаете (во всяком случае, я на это надеюсь).
🎥 Видео
3 14 Уравнения МаксвеллаСкачать

Уравнения Максвелла 2021Скачать

Электромагнитные волны и уравнения Максвелла — Эмиль АхмедовСкачать

Уравнения Максвелла — Мартин МакколлСкачать

3 Уравнения Максвелла в дифференциальной формеСкачать

Лекция 233 оператор набла. Уравнения МаксвеллаСкачать

О чем говорят уравнения Максвелла? Видео 2/2Скачать

Вывод уравнений МаксвеллаСкачать

Джеймс Клерк Максвелл. Научные труды и вклад в наукуСкачать

Электродинамика | уравнения Максвелла | 1 | для взрослыхСкачать
Физические ошибки. Уравнения МаксвеллаСкачать

60. Уравнения МаксвеллаСкачать

Уравнения Максвелла Лекция 10-1Скачать

Ацюковский: Уравнения Максвелла эту задачу не решают!Скачать


