Количественная зависимость константы скорости реакции от температуры была впервые предложена тоже Я.Вант-Гоффом (1887) в виде уравнений изохоры и изобары химической реакции (см. п. 4.5.2).
Эта идея была развита С.Аррениусом (1889), который открыл, что температурную зависимость скорости многих реакций можно описать уравнением:
k = Ае — Е* / RT
где k — константа скорости, e — основание натуральных логарифмов, R — универсальная газовая постоянная, T – температура, А — предэкспоненциальный множитель, Е* — энергия активации реакции.
Чтобы выяснить физический смысл величин А и Е*, входящих в уравнение Аррениуса, следует сначала познакомиться с основными положениями теории активных соударений(столкновений)(С.Аррениус и Я.Вант-Гофф; 1880-е г.г.):
1) Химическое взаимодействие между молекулами возможно только при их столкновении.
2) Не каждое столкновение молекул приводит к химическому взаимодействию, т. е. является результативным или, по терминологии Аррениуса, активным. Существует некий энергетический барьер, преодолеть который и вступить во взаимодействие может лишь часть молекул, причём, как правило, это очень малая часть от их общего числа в системе.
3) Причиной, обусловливающей существование энергетического барьера, является взаимное отталкивание электронных оболочек молекул при их сближении.
Когда две частицы удалены друг от друга на очень большое расстояние, между ними нет никакого взаимодействия и потенциальная энергия такой системы равна нулю. При меньших расстояниях между частицами они притягиваются друг к другу, и потенциальная энергия системы понижается. При дальнейшем уменьшении расстояния становятся заметными силы отталкивания электронных оболочек молекул и потенциальная энергия резко возрастает. Поэтому для сближения частиц до расстояния, на котором начнется перераспределение электронов на их орбиталях (т. е. химическое взаимодействие), частицы должны обладать достаточно большим запасом кинетической энергии. Силы отталкивания между частицами и представляют между собой так называемый потенциальный или энергетический барьер, а химическое взаимодействие возможно только в том случае, если сталкивающиеся молекулы способны преодолеть его.
4) Для того, чтобы молекулы могли при столкновении преодолеть энергетический барьер, они должны двигаться навстречу друг другу с достаточно большой скоростью. Для достижения этой необходимой скорости нужна определённая энергия, называемая энергией активации. Энергия активацииЕ* — это избыток энергии активных молекул по сравнению с неактивными, или иначе, энергия, которой должны обладать молекулы, чтобы иметь возможность вступить во взаимодействие. Размерность СИ энергии активации — Дж/моль.
5) Чем больше энергия активации реакции, тем больше энергетический барьер, и тем меньшее число молекул способно его преодолеть. Поэтому, чем больше Е*, тем медленнее идёт реакция.
6) С повышением температуры увеличивается скорость теплового движения молекул, поэтому доля активных молекул возрастает. Иными словами, при повышении температуры происходит термическая активация, приводящая к увеличению скорости реакции.
Возвращаясь к уравнению Аррениуса, отметим, что величина e — Е* / RT (“экспонента”) равна доле активных молекул, обладающих избыточной энергией Е* для вступления в химическое взаимодействие, а коэффициент А (предэкспоненциальный множитель) равен полной частоте соударений между молекулами реагирующих веществ в реакционном объёме.
Логарифмируя уравнение Аррениуса, получим уравнение прямой, не проходящей через начало координат:
| E* ln k = ln A — ¾¾ . RT |
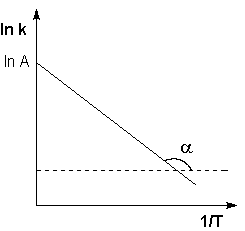
Построив по экспериментальным данным график зависимости ln k от 1/T (т. н. “аррениусовскую зависимость”), можно вычислить энергию активации изучаемой реакции по тангенсу угла наклона, который в этом случае равен —Е*/R (рис. 12.5).
 Рис. 12.5. Аррениусовская зависимость и энергия активации Рис. 12.5. Аррениусовская зависимость и энергия активации |
Дифференцируя логарифмическую форму уравнения Аррениуса по температуре, получим уравнение, подобное уравнению изобары (изохоры) Вант-Гоффа:
| d ln k E* ¾¾¾ =¾¾ dT RT 2 |
Интегрирование его в пределах k1 ¸ k2 и Т1 ¸ Т2 приводит к уравнению
| k2 E* 1 1 ln ¾ = ¾ (¾ — ¾) k1 R T2 T1 |
| k2 E* Т2 — Т1 ln ¾ =¾ ( ¾¾¾) , (12.11) k1 R T1 T2 |
где k1 и k2 — константы скорости данной реакции при температурах T1 и T2 соответственно.
С помощью уравнения (12.11), также называемого уравнением Аррениуса, можно вычислить константу скорости k2 при заданной температуре Т2, если известны значения константы скорости k1 при температуре Т1 и энергия активации реакции Е*. Кроме того, это уравнение позволяет вычислить энергию активации реакции по значениям двух констант скорости при различных температурах:
| R T1 T2 k2 E* = ¾¾¾¾ ln¾ . Т2 — Т1 k1 |
Таким образом, в соответствии с теорией активных соударений повышение температуры увеличивает скорость химических реакций потому, что при этом возрастает доля активных молекул, способных преодолеть потенциальный барьер при столкновении.
Видео:Какой физический смысл экспоненты? - Мыслить №133Скачать

Физический смысл экспоненты в уравнении аррениуса
ФИЗИЧЕСКАЯ И КОЛЛОИДНАЯ ХИМИЯ
Конспект лекций для студентов биофака ЮФУ (РГУ)
2.1 СКОРОСТЬ ХИМИЧЕСКОЙ РЕАКЦИИ
2.1.9 Влияние температуры на константу скорости реакции
Константа скорости реакции есть функция от температуры; повышение температуры, как правило, увеличивает константу скорости. Первая попытка учесть влияние температуры была сделана Я. Г. Вант-Гоффом, который сформулировал следующее эмпирическое правило:
При повышении температуры на каждые 10 градусов константа скорости элементарной химической реакции увеличивается в 2 – 4 раза.
Величина, показывающая, во сколько раз увеличивается константа скорости при повышении температуры на 10 градусов, есть температурный коэффициент константы скорости реакции γ . Математически правило Вант-Гоффа можно записать следующим образом:
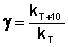
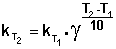
Однако правило Вант-Гоффа применимо лишь в узком температурном интервале, поскольку температурный коэффициент скорости реакции γ сам является функцией от температуры; при очень высоких и очень низких температурах γ становится равным единице (т.е. скорость химической реакции перестает зависеть от температуры).
2.1.10 Уравнение Аррениуса
Очевидно, что взаимодействие частиц осуществляется при их столкновениях; однако число столкновений молекул очень велико и, если бы каждое столкновение приводило к химическому взаимодействию частиц, все реакции протекали бы практически мгновенно. С. Аррениус постулировал, что столкновения молекул будут эффективны (т.е. будут приводить к реакции) только в том случае, если сталкивающиеся молекулы обладают некоторым запасом энергии – энергией активации.
Энергия активации есть минимальная энергия, которой должны обладать молекулы, чтобы их столкновение могло привести к химическому взаимодействию.
Рассмотрим путь некоторой элементарной реакции
Поскольку химическое взаимодействие частиц связано с разрывом старых химических связей и образованием новых, считается, что всякая элементарная реакция проходит через образование некоторого неустойчивого промежуточного соединения, называемого активированным комплексом:
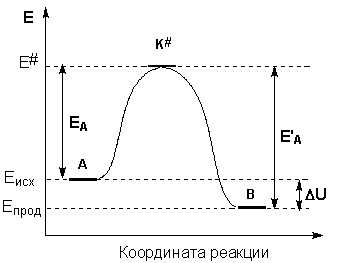
Образование активированного комплекса всегда требует затраты некоторого количества энергии, что вызвано, во-первых, отталкиванием электронных оболочек и атомных ядер при сближении частиц и, во-вторых, необходимостью построения определенной пространственной конфигурации атомов в активированном комплексе и перераспределения электронной плотности. Таким образом, по пути из начального состояния в конечное система должна преодолеть своего рода энергетический барьер. Энергия активации реакции приближённо равна превышению средней энергии активированного комплекса над средним уровнем энергии реагентов. Очевидно, что если прямая реакция является экзотермической, то энергия активации обратной реакции Е’А выше, нежели энергия активации прямой реакции EA. Энергии активации прямой и обратной реакции связаны друг с другом через изменение внутренней энергии в ходе реакции. Вышесказанное можно проиллюстрировать с помощью энергетической диаграммы химической реакции (рис. 2.5).
Рис. 2.5 Энергетическая диаграмма химической реакции.
Eисх – средняя энергия частиц исходных веществ,
Eпрод – средняя энергия частиц продуктов реакции
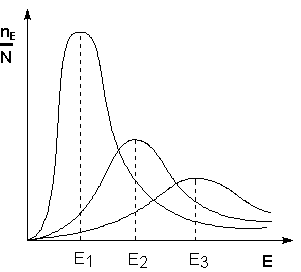
Поскольку температура есть мера средней кинетической энергии частиц, повышение температуры приводит к увеличению доли частиц, энергия которых равна или больше энергии активации, что приводит к увеличению константы скорости реакции (рис.2.6):
Рис. 2.6 Распределение частиц по энергии
Здесь nЕ/N – доля частиц, обладающих энергией E;
Ei — средняя энергия частиц при температуре Ti (T1 уравнения Аррениуса . Согласно уравнению изобары Вант-Гоффа,
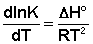
Поскольку константа равновесия есть отношение констант скоростей прямой и обратной реакции, можно переписать выражение (II.31) следующим образом:
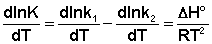
Представив изменение энтальпии реакции ΔHº в виде разности двух величин E1 и E2, получаем:
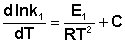
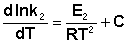
Здесь С – некоторая константа. Постулировав, что С = 0, получаем уравнение Аррениуса, где EA – энергия активации :
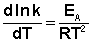
После неопределенного интегрирования выражения (II.35) получим уравнение Аррениуса в интегральной форме:
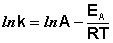
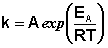
Рис. 2.7 Зависимость логарифма константы скорости химической
реакции от обратной температуры.
Здесь A – постоянная интегрирования. Из уравнения (II.37) нетрудно показать физический смысл предэкспоненциального множителя A, который равен константе скорости реакции при температуре, стремящейся к бесконечности. Как видно из выражения (II.36), логарифм константы скорости линейно зависит от обратной температуры (рис.2.7); величину энергии активации EA и логарифм предэкспоненциального множителя A можно определить графически (тангенс угла наклона прямой к оси абсцисс и отрезок, отсекаемый прямой на оси ординат).
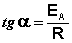
Зная энергию активации реакции и константу скорости при какой-либо температуре T1, по уравнению Аррениуса можно рассчитать величину константы скорости при любой температуре T2:
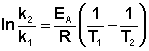
Copyright © С. И. Левченков, 1996 — 2005.
Видео:Лекция 10. Экспонента и её смысл.Скачать

АРРЕ́НИУСА УРАВНЕ́НИЕ
В книжной версии
Том 2. Москва, 2005, стр. 272
Скопировать библиографическую ссылку:
АРРЕ́НИУСА УРАВНЕ́НИЕ, описывает зависимость константы скорости химической реакции от температуры в виде: $k = A·text(–E_a/RT)$, где $A$ – предэкспоненциальный множитель, $E_a$ – энергия активации , $R$ – газовая постоянная, $T$ – абсолютная темп-ра. Предложено С. Аррениусом в 1889. Множитель $text (–E_a/RT)$ для простой реакции представляет собой долю молекул с энергией, достаточной, чтобы произошла реакция. График зависимости $ln k$ от $1/T$ – прямая линия: численные значения $A$ и $E_a$ определяют по значению начальной ординаты и тангенса угла наклона этой прямой. Множитель $A$ изменяется в диапазоне 10 13 –10 15 с –1 для мономолекулярных и 10 6 –10 10 дм 3 · моль –1 · с –1 для бимолекулярных реакций. Энергия активации большинства реакций составляет величину 10–100 кДж/моль. Для сложных реакций определяемая $E_a$ – эффективная величина, которая является функцией энергий активаций отд. стадий, зависит от темп-ры, может принимать отрицат. значения. В широком интервале температур бимолекулярные реакции лучше описываются уравнением: $k=BT^n·text (–E_a/RT)$ . В некоторых случаях, напр. для быстрых реакций, реакций в вязких средах, реакций с туннельным эффектом, А. у. неприменимо.
📸 Видео
Число e - 2,718. Объяснение математического смысла.Скачать

Что же это такое - ЧИСЛО Е и экспонента ??? Простым языком!)Скачать

ДВИ по химии. Термохимия. Уравнение Аррениуса, закон Гесса, задачи на теплоемкостьСкачать

Уравнение Аррениуса, часть 1Скачать

Влияние температуры на скорость химических реакций. 10 класс.Скачать

Физический смысл производной с НУЛЯ /подробно и легкоСкачать

Лекция 8: уравнение Аррениуса (30.10.2019)Скачать

Использование уравнения Аррениуса для решения задач (1/2). Химия для поступающих.Скачать

ФИЗИЧЕСКИЙ СМЫСЛ ПРОИЗВОДНОЙ. Подготовка к ЕГЭ по математике с Артуром ШарифовымСкачать

✓ Число e на пальцах | Ботай со мной #054 | Борис Трушин |Скачать

2. Определение производной. Геометрический и физический смысл производной.Скачать

Геометрический смысл производной | КасательнаяСкачать

Теории кислот, оснований и растворов. Теория Аррениуса-Оствальда. 11 класс.Скачать

ЭкспонентаСкачать

6 Уравнение Аррениуса, ч 2Скачать

Геометрический смысл производной. Уравнение касательнойСкачать

20. (В-У). Температурная зависимость скорости реакцииСкачать

Тема: Логарифм. Экспонента. Урок: Элементарные функции. Экспонента.Скачать