Читайте также:
|
. Для точки М:
заданы в табл. 5. Варианты фигурных пластинок заданы в табл. 6.| № варианта | 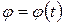 | а, см | R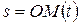, см |  , см |
 | — | — |  | |
 | — | — |  | |
 | — | — |  | |
 | — | — |  | |
 | — | — |  | |
 | — | — |  | |
 | — |  | ||
 | — |  | ||
 | — |  | ||
 | — |  | ||
 | — |  | ||
 | — |  | ||
 | — |  | ||
 | — | | ||
| | — |  | ||
 | — |  | ||
| | — | — |  | |
 | — |  |
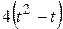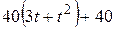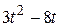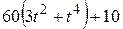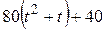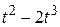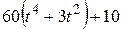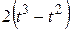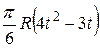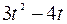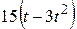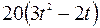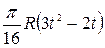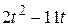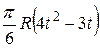Окончание табл. 5
| № варианта | 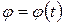| а, см | R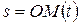, см | , см |
 | — |  | ||
 | — |  | ||
| | — |  | ||
| | — |  | ||
 | — |  | ||
 | — |  | ||
| | — |  | ||
 | — | — | | |
 | — |  | ||
 | — | | ||
 |  | |||
 |  |
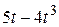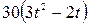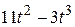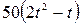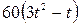Для выполнения и защиты данной задачи необходимо усвоить материал п. 6 рабочей программы. Требуется решить следующие задачи из сборника задач [3]:
1) траектория и уравнения движения точки: 10.1 – 10.5;
2) скорость и ускорение точки: 11.1 – 11.7, 12.1, 12.6, 12.13, 12.16, 12.22;
3) вращение твердого тела вокруг неподвижной оси: 13.1 – 13.5, 13.18, 13.19;
4) преобразование простейших движений твердого тела: 14.1 – 14.5.
5) сложное движение точки, сложение скоростей: 22.1, 22.3, 22.9;
6) сложение ускорений точки: 23.1, 23.3, 23.4.
 |  |
 |  |
 |  |
Продолжение табл. 6
 |  |
 |  |
 |  |
Продолжение табл. 6
 |  |
 |  |
 |  |
Продолжение табл. 6
 |  |
 |  |
 |  |
Окончание табл. 6
Дата добавления: 2015-04-15 ; просмотров: 17 ; Нарушение авторских прав
- Сложное движение точки
- Сложное движение точки. Пример решения задачи
- Условие задачи
- Решение задачи
- Определение положения точки
- Определение абсолютной скорости точки
- Определение относительной скорости точки
- Определение переносной скорости точки
- Определение абсолютной скорости точки
- Определение абсолютного ускорения точки
- Определение относительного ускорения
- Определение переносного ускорения
- Определение кориолисова ускорения
- Определение абсолютного ускорения
- 💥 Видео
Видео:Урок 44. Вращение твердого тела. Линейная и угловая скорость. Период и частота вращения.Скачать
Сложное движение точки
Задача 3. Сложное движение точки
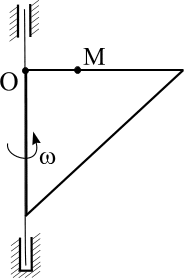
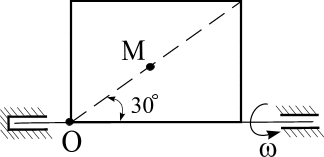
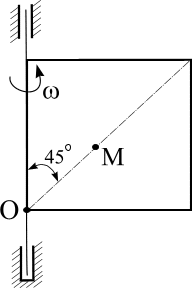
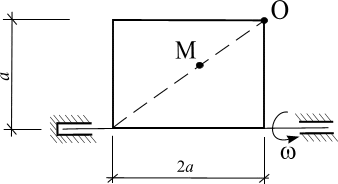
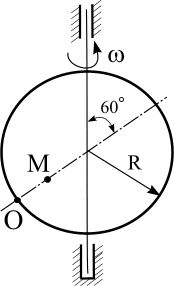
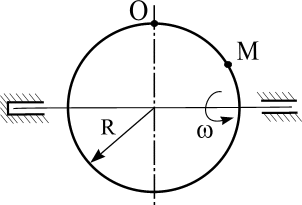
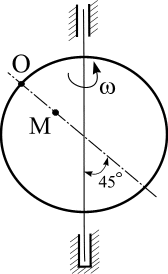
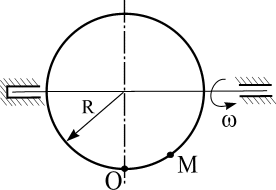
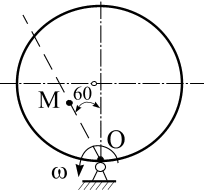
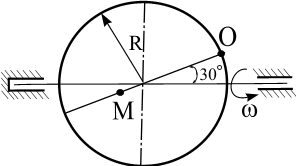
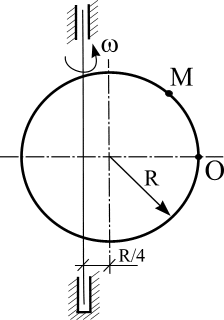
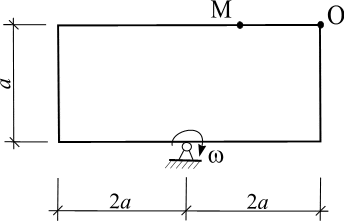
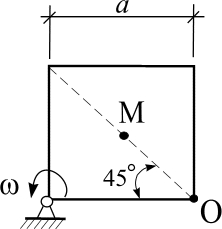
Пластинка вращается по заданному уравнению ? = ?(t). По пластин-
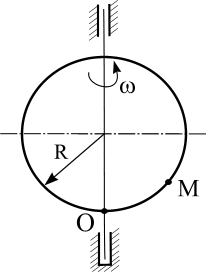
ке вдоль прямой ОМ (сторона квадратной пластины а = 40 см) или радиусу
R ( R = 40 см) движется точка М. Движение точки М задано уравнениями
S (t ) ? OM (t ). Вычислить для точки М:
. абсолютную скорость в момент времени t = 1с, показать на рисунке
векторы относительной, переносной и абсолютной скоростей;
. абсолютное ускорение в момент времени t = 1с, показать на рисунке
направление векторов относительного, переносного ускорений, а также ускорения Кориолиса.
Функциональные зависимости ? = ?(t) в радианах заданы в табл. 5,
фигурные пластинки и уравнение движения точки ОМ = ОМ(t) в сантиметрах заданы в табл. 6.
Видео:§64 Поверхности вращенияСкачать
Сложное движение точки. Пример решения задачи
Теория, применяемая для решения приведенной ниже задачи, излагается на странице “Сложное движение точки, теорема Кориолиса”.
Видео:Вращательное движение. 10 класс.Скачать
Условие задачи
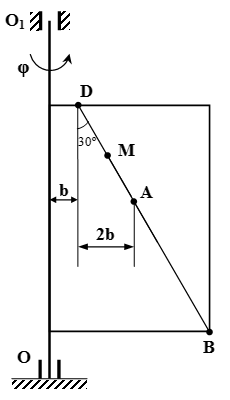
Прямоугольная пластина вращается вокруг неподвижной оси по закону φ = 6 t 2 – 3 t 3 . Положительное направление отсчета угла φ показано на рисунках дуговой стрелкой. Ось вращения OO 1 лежит в плоскости пластины (пластина вращается в пространстве).
По пластине вдоль прямой BD движется точка M . Задан закон ее относительного движения, т. е. зависимость s = AM = 40( t – 2 t 3 ) – 40 ( s — в сантиметрах, t — в секундах). Расстояние b = 20 см . На рисунке точка M показана в положении, при котором s = AM > 0 (при s 0 точка M находится по другую сторону от точки A ).
Найти абсолютную скорость и абсолютное ускорение точки M в момент времени t 1 = 1 с .
Указания. Эта задача – на сложное движение точки. Для ее решения необходимо воспользоваться теоремами о сложении скоростей и о сложении ускорений (теорема Кориолиса). Прежде чем производить все расчеты, следует по условиям задачи определить, где находится точка M на пластине в момент времени t 1 = 1 с , и изобразить точку именно в этом положении (а не в произвольном, показанном на рисунке к задаче).
Видео:Сферическое движениеСкачать
Решение задачи
Дано: b = 20 см , φ = 6 t 2 – 3 t 3 , s = |AM| = 40( t – 2 t 3 ) – 40 , t 1 = 1 c .
Определение положения точки
Определяем положение точки в момент времени t = t 1 = 1 c .
s = 40( t 1 – 2 t 1 3 ) – 40 = 40(1 – 2·1 3 ) – 40 = –80 см.
Поскольку s 0 , то точка M ближе к точке B, чем к D.
|AM| = |–80| = 80 см.
Делаем рисунок.
Определение абсолютной скорости точки
Согласно теореме о сложении скоростей, абсолютная скорость точки равна векторной сумме относительной и переносной скоростей:
.
Определение относительной скорости точки
Определяем относительную скорость . Для этого считаем, что пластина неподвижна, а точка M совершает заданное движение. То есть точка M движется по прямой BD . Дифференцируя s по времени t , находим проекцию скорости на направление BD :
.
В момент времени t = t 1 = 1 с ,
см/с.
Поскольку , то вектор направлен в направлении, противоположном BD . То есть от точки M к точке B . Модуль относительной скорости
vот = 200 см/с .
Изображаем вектор на рисунке.
Определение переносной скорости точки
Определяем переносную скорость . Для этого считаем, что точка M жестко связана с пластиной, а пластина совершает заданное движение. То есть пластина вращается вокруг оси OO1. Дифференцируя φ по времени t , находим угловую скорость вращения пластины:
.
В момент времени t = t 1 = 1 с ,
.
Поскольку 0″ style=»width:48px;height:18px;vertical-align:-10px;background-position:-583px -267px»> , то вектор угловой скорости направлен в сторону положительного угла поворота φ , то есть от точки O к точке O1. Модуль угловой скорости:
ω = 3 с -1 .
Изображаем вектор угловой скорости пластины на рисунке.
Из точки M опустим перпендикуляр HM на ось OO1.
При переносном движении точка M движется по окружности радиуса |HM| с центром в точке H .
|HM| = |HK| + |KM| = 3 b + |AM| sin 30° = 60 + 80·0,5 = 100 см ;
Переносная скорость:
vпер = ω|HM| = 3·100 = 300 см/с .
Вектор направлен по касательной к окружности в сторону вращения.
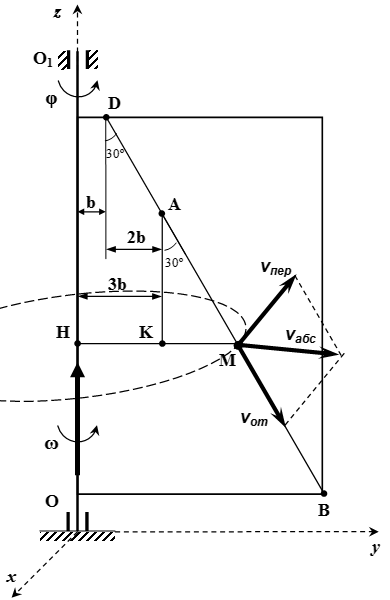
Определение абсолютной скорости точки
Определяем абсолютную скорость . Абсолютная скорость точки равна векторной сумме относительной и переносной скоростей:
.
Проводим оси неподвижной системы координат Oxyz . Ось z направим вдоль оси вращения пластины. Пусть в рассматриваемый момент времени ось x перпендикулярна пластине, ось y лежит в плоскости пластины. Тогда вектор относительной скорости лежит в плоскости yz . Вектор переносной скорости направлен противоположно оси x . Поскольку вектор перпендикулярен вектору , то по теореме Пифагора, модуль абсолютной скорости:
.
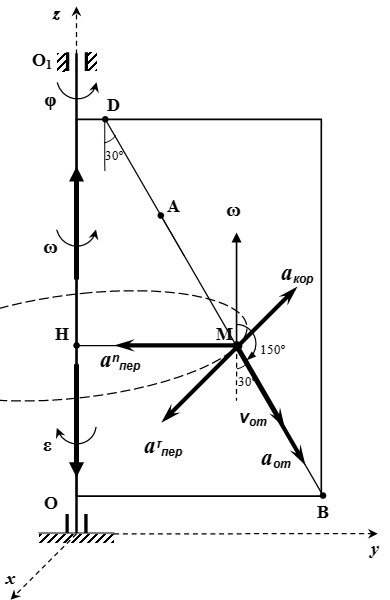
Определение абсолютного ускорения точки
Согласно теореме о сложении ускорений (теорема Кориолиса), абсолютное ускорение точки равно векторной сумме относительного, переносного и кориолисова ускорений:
,
где
– кориолисово ускорение.
Определение относительного ускорения
Определяем относительное ускорение . Для этого считаем, что пластина неподвижна, а точка M совершает заданное движение. То есть точка M движется по прямой BD . Дважды дифференцируя s по времени t , находим проекцию ускорения на направление BD :
.
В момент времени t = t 1 = 1 с ,
см/с 2 .
Поскольку , то вектор направлен в направлении, противоположном BD . То есть от точки M к точке B . Модуль относительного ускорения
aот = 480 см/с 2 .
Изображаем вектор на рисунке.
Определение переносного ускорения
Определяем переносное ускорение . При переносном движении точка M жестко связана с пластиной, то есть движется по окружности радиуса |HM| с центром в точке H . Разложим переносное ускорение на касательное к окружности и нормальное ускорения:
.
Дважды дифференцируя φ по времени t , находим проекцию углового ускорения пластины на ось OO 1 :
.
В момент времени t = t 1 = 1 с ,
с –2 .
Поскольку , то вектор углового ускорения направлен в сторону, противоположную положительного угла поворота φ , то есть от точки O1 к точке O. Модуль углового ускорения:
ε = 6 с -2 .
Изображаем вектор углового ускорения пластины на рисунке.
Переносное касательное ускорение:
a τ пер = ε |HM| = 6·100 = 600 см/с 2 .
Вектор направлен по касательной к окружности. Поскольку вектор углового ускорения направлен в сторону, противоположную положительного угла поворота φ , то направлен в сторону, противоположную положительному направлению поворота φ . То есть направлен в сторону оси x .
Переносное нормальное ускорение:
a n пер = ω 2 |HM| = 3 2 ·100 = 900 см/с 2 .
Вектор направлен к центру окружности. То есть в сторону, противоположную оси y .
Определение кориолисова ускорения
Кориолисово (поворотное) ускорение:
.
Вектор угловой скорости направлен вдоль оси z . Вектор относительной скорости направлен вдоль прямой |DB| . Угол между этими векторами равен 150° . По свойству векторного произведения,
.
Направление вектора определяется по правилу буравчика. Если ручку буравчика повернуть из положения в положение , то винт буравчика переместится в направлении, противоположном оси x .
Определение абсолютного ускорения
Абсолютное ускорение:
.
Спроектируем это векторное уравнение на оси xyz системы координат.
;
;
.
Модуль абсолютного ускорения:
.
Абсолютная скорость ;
абсолютное ускорение .
Автор: Олег Одинцов . Опубликовано: 10-01-2016
💥 Видео
Пластика (Решение задач на пластинку)Скачать
Скорости точек плоской фигурыСкачать
Геометрия 9 класс (Урок№34 - Тела и поверхности вращения.)Скачать
Сложное движение точки. Решение задачи. Авторы: Ермишин Степан, Ходунов Алексей, Хужаев ДмитрийСкачать
Задача 3Скачать
Решение графических задач на равномерное движениеСкачать
Урок 50. Задачи на вращение с пост. угловым ускорениемСкачать
угловая СКОРОСТЬ формула угловое УСКОРЕНИЕ 9 классСкачать
Кинематика точки Задание К1Скачать
Угловая скорость, угловое ускорениеСкачать
Четвертьволновая пластинкаСкачать
Кинематика. 4.1. Сложное движение точки на примере пластинки. Определение абсолютной скорости точки.Скачать
Дифракция - 11. Задача И4.117 (дифракция Френеля, пластинка с выемкой)Скачать
Определение скорости и ускорения при поступательном и вращательном движении.Скачать
Скорости и ускорения точек механизмаСкачать
Сложное движение точки. Задача 1Скачать
