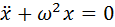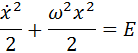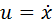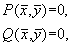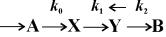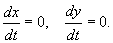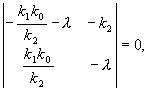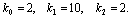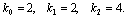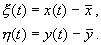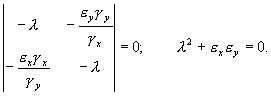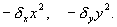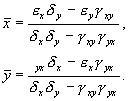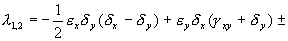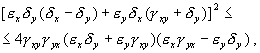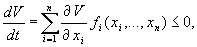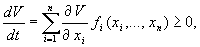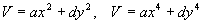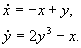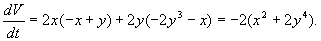Фазовый портрет уравнения второго порядка

Дата добавления: 2014-04-22 ; просмотров: 7086 ; Нарушение авторских прав

Для получения уравнений, описывающих фазовый портрет системы второго порядка, необходимо в системе дифференциальных уравнений (12.6) второе уравнение поделить на первое и исключить из рассмотрения время t, в результате чего получают:

. (13.3)

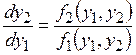
Решение этого уравнения дает семейство интегральных кривых на фазовой плоскости, по которым строят фазовые траектории системы.

Фазовые портреты линейных систем второго порядка классифицируют по типам особых точек.

Линейную систему второго порядка описывают уравнением

, (13.4)

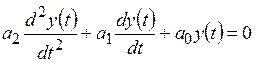
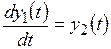
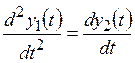
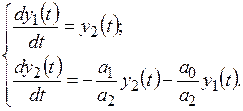
где y(t) − выходная координата системы; а₀, а₁, a₂ − постоянные коэффициенты. Обозначив y(t) = y₁(t), , тогда и уравнение (13.1) можно записать

(13.5)

Разделив второе уравнение на первое, получают

, (13.6)

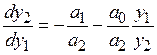
решением которого будет уравнение фазовых траекторий

где с_i − постоянные интегрирования.

Возможны шесть различных типов фазовых траекторий в зависимости от корней характеристического уравнения a₂s 2 + a₁s + a₀ = 0.

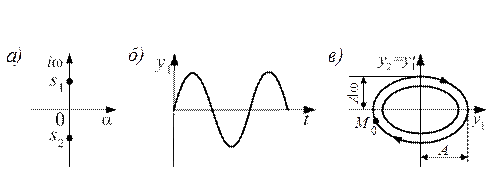
Случай 1. Корни − мнимые при a₁=0, a₀>0, a₂>0; s_1,2=±iω; .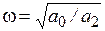

Система находится на границе устойчивости.

График y₁(t) показан на рис. 13.1. Для получения уравнения фазовой траектории выражения (13.8) и (13.9) возводят в квадрат и складывают, в результате получают уравнение

. (13.10)

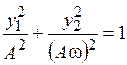
Незатухающим периодическим колебаниям в системе соответствует на фазовой плоскости замкнутая фазовая траектория. Особая точка системы является геометрическим центром фазовых траекторий и носит название центр, а сама система называется консервативной.

Рис. 13.1. Фазовый портрет типа центр: а) плоскость корней

характеристического уравнения; б) переходный процесс; в) фазовый портрет

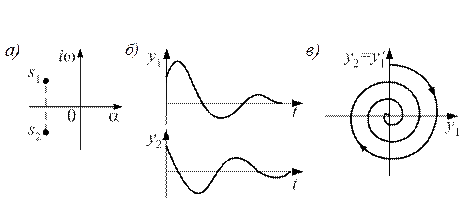
Случай 2. Корни − комплексные и имеют отрицательные вещественные части при а₁ 0, a₁ > 0, а₂ > 0: s₁,₂ = −α ± iω (рис. 13.2а),

α = −a₁/(2а₂), 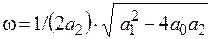− система устойчива.

Решение уравнения (13.4) имеет вид

где d = arctg(a/w); .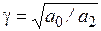

Рис. 13.2. Фазовый портрет типа устойчивый фокус: а) расположение корней

характеристического уравнения; б) переходный процесс; в) фазовый портрет

Уравнения (13.11) и (13.12) дают в фазовой плоскости параметрическое уравнение спиралей. С каждым оборотом, соответствующим одному периоду колебаний, изображающая точка приближается к началу координат, так как значения y₁ и y₂за период колебаний становятся меньше.

Особая точка называется устойчивым фокусом.

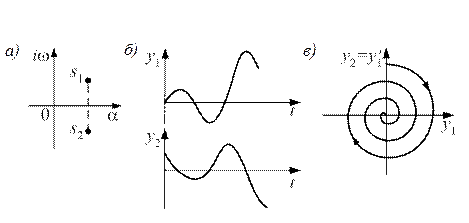
Случай 3.Корни − комплексные и имеют положительные вещественные части при а₁ 0, a₁ 0: s₁,₂ = α ± iω (рис. 13.3а), система неустойчива. Откуда

Рис. 13.3 Фазовый портрет типа неустойчивый фокус: а) расположение корней

характеристического уравнения; б) переходный процесс; в) фазовый портрет

Состоянию неустойчивого равновесия системы соответствует особая точка, которая называется неустойчивый фокус (рис. 13.3в). В системе возникает колебательный процесс с возрастающей амплитудой.

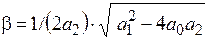
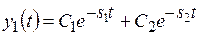
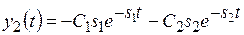
Случай 4. Корни – вещественные отрицательные при а₁ > 4а₀a₂; a₀ > 0, a₁ > 0, а₂ > 0: s₁,₂ = −α±b (рис. 13.4а), α = a₁/(2а₂), − система устойчива. Этот случай соответствует апериодическому процессу в системе, сама система устойчива. Решение уравнения (13.14)

; (13.15)

. (13.16)

Границей областей с переходными процессами типа 1 и 2 служат прямые с уравнениями y₂ = −s₂y₁ и y₂ = −s₁y₁.

Все фазовые траектории вливаются в начало координат − особую точку, называемую устойчивым узлом (рис. 13.4). Время движения к состоянию равновесия теоретически равно бесконечности.

Рис. 13.4. Фазовый портрет типа устойчивый узел: а) расположение корней

характеристического уравнения; б) переходный процесс; в) фазовый портрет

Случай 5. Корни − вещественные положительные при а₁>4а₀a₂; a₀>0, a₁ 0: s₁,₂ = α ± b (рис. 13.5а), система неустойчива. Решение уравнения (13.4):

; (13.17)

. (13.18)

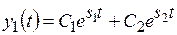
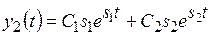
Рис. 13.5. Фазовый портрет типа неустойчивый узел: а) расположение корней

характеристического уравнения; б) переходный процесс; в) фазовый портрет

Фазовые траектории направлены от начала координат в бесконечность. Особая точка носит название неустойчивый узел (рис. 13.5). Крайние траектории определяются уравнениями y₂ = s₁y₁ и y₂ = s₂y₁.

Случай 6. Корни − вещественные и имеют различные знаки при a₀ 0, a₂ > 0: s₁ = −α₁, s₂ = β. В этом случае система неустойчива.

Частным является случай, когда a₁=0, и, учитывая, что a₀

Видео:Дополнительные главы ИДУ: Построение фазовых портретов | Занятие 3Скачать

Фазовые портреты «на пальцах» или что можно узнать о решениях диффура, не решая его

Очень часто в ряде наук встречается ситуация, когда модель рассматриваемого процесса сводится к дифференциальному уравнению. Причём, в большинстве реальных задач это уравнение довольно сложно решить, или совсем невозможно. И вот тут в полный голос звучит извечный вопрос: как быть?

Встречайте: фазовые портреты (они же фазовые диаграммы). Простым языком, фазовый портрет — это то, как величины, описывающие состояние системы (a.k.a. динамические переменные), зависят друг от друга. В случае механического движения это координата и скорость, в электричестве это заряд и ток, в известной популяционной задаче это количество хищников и жертв и т.д.

Чем хороши фазовые портреты? А тем, что их можно построить не решая динамические уравнения системы. В некоторых случаях построение фазового портрета становится совсем простой задачей. Однако, одновременно с этим, фазовые портреты дают вдумчивому наблюдателю очень много информации о поведении системы.

Начнём с простого примера — малых колебаний (так же называемых гармоническими). Малые колебания встречаются почти в каждой сфере естественных наук. Для определённости, будем рассматривать колебания металлического стержня, подвешенного за один из концов (частный случай так называемого физического маятника). Можно показать, что его колебания описываются следующим дифференциальным уравнением:

Где x — угол отклонения стержня от вертикали, точка над x означает производную по времени, а коэффициент перед синусом зависит от размера и массы стержня.

Если амплитуда (размах) колебаний достаточно мала, синус можно приближенно заменить его аргументом (вы ведь помните первый замечательный предел, нет?). В таком случае, уравнение принимает следующий вид:

Это уравнение легко решается регулярными методами, но, давайте, попробуем применить к нему метод фазовых портретов. Для этого, домножим уравнение на производную и проинтегрируем его один раз по времени:

Получилось выражение, первый член которого выглядит как кинетическая энергия. Это не случайно — на самом деле мы получили именно закон сохранения энергии. Постоянная Е в правой части (полная энергия системы на единицу массы) может принимать различные значения, которые соответствуют разным начальным состояниям системы.

Полученный нами закон сохранения превратился в уравнение кривой на плоскости (x,u):

Для разных значений Е мы получим разные кривые. Нарисуем несколько таких линий для разных значений энергии:

По горизонтальной оси отложена величина x, по вертикальной — u

Каждая из полученных линий называется фазовой траекторией. Когда меняется состояние системы, изображающая её точка движется по одной из этих траекторий, стрелки указывают направление движения изображающей точки.

По графику видно, что значения скорости и координаты меняются циклическим образом, то есть периодически повторяются. Отсюда можно сделать вывод, что описываемая рассмотренным уравнением система будет совершать колебания. Бинго! Именно так ведёт себя маятник, и если решить уравнение, решение будет иметь вид периодических функций (а именно — комбинации синуса и косинуса).

Следует однако помнить, что замена синуса его аргументом оправдана лишь для малых углов отклонения (от 10 градусов и меньше), поэтому мы не можем доверять тем траекториям, которые выходят за границы области, ограниченной жирными пунктирными линиями, то есть из четырех приведенных траекторий лишь оранжевая достоверно отображает реальность. Кроме того, поскольку x это угол, то его значения, соответствующие 180 и -180 градусам описывают одно и то же положение стержня, то есть правая и левая пунктирные линии (тонкие) на графике это на самом деле одна и та же линия.

Теперь, поскольку нам понятна суть, можно перейти к чему-то посложнее. Выше мы очень сильно упростили уравнение и при этом ограничили себя только малыми колебаниями. Математик бы сказал, что мы линеаризовали уравнение и пренебрегли нелинейными эффектами. Так давайте включим в рассмотрение нелинейность. Вернёмся к самому первому уравнению — с синусом. Если мы повторим с ним то, что проделали с линейным уравнением, мы получим следующий закон сохранения:

В зависимости от значения энергии, мы опять получаем разные кривые, которые приведены на следующем рисунке, причем выбраны те же значения энергии, что и на первой диаграмме, и те же цвета для линий.

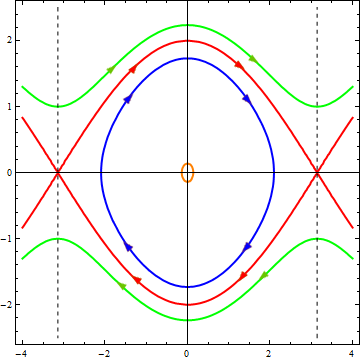
По горизонтальной оси отложена величина x, по вертикальной — u

Как видите, процессы происходящее в системе стали более разнообразными:

При малых энергиях (оранжевая и синяя траектории) существует колебательный режим, но колебания уже не являются гармоническими — фазовые траектории уже не имеют форму эллипсов.

При больших энергиях (зеленая траектория) колебаний уже нет, вместо этого мы получаем вращательное движение с переменной скоростью. И действительно, если достаточно сильно «толкнуть» стержень, он будет вращаться, замедляясь при подъёме и ускоряясь при спуске.

При определенном промежуточном значении энергии получается особый набор траекторий, которые отделяют друг от друга области соответствующие разным типам движения и поэтому называются сепаратрисами. И да, значение энергии для красной кривой было выбрано мной именно так, чтобы в нелинейном случае получилась сепаратриса. Каждая ветвь сепаратрисы это траектория, соответствующая особому типу движения. Посмотрим на диаграмму: движение начинается с очень маленькой скоростью от одного крайнего положения стержня, при приближении к положению равновесия скорость растёт, а после изображающая точка все более замедляясь уходит к крайнему положению, где и останавливается. Это соответствует тому, что мы поднимаем стержень вертикально вверх и отпускаем его, проносясь через положение равновесия он поднимается к верхней точке с другой стороны и останавливается.

А теперь давайте посмотрим насколько близки к истине наши выводы, сделанные на основе фазовых портретов. Перед вами график решения линейного уравнения:

По горизонтальной оси отложено время, по вертикальной — x

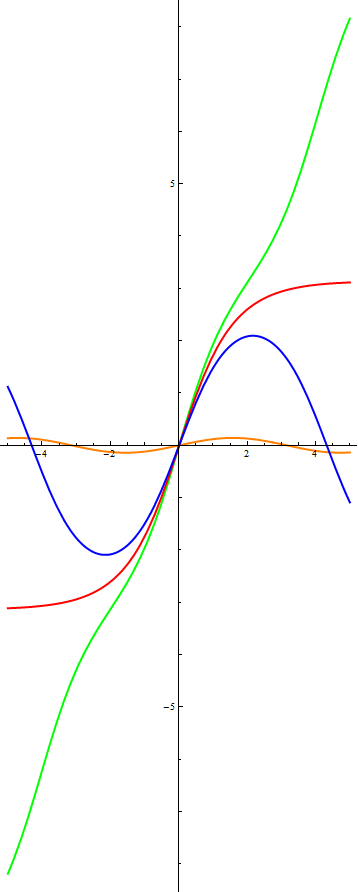
По горизонтальной оси отложено время, по вертикальной — x

Цветовая маркировка на этих графиках такая же, как и на фазовых портретах. Судить о том, насколько верные выводы были сделаны на основе фазовых портретов я предоставлю вам, дорогие читатели. Обращу ваше внимание только на один момент — колебания в линейном случае происходят синхронно — с одной и той же частотой. В нелинейном же случае, частота колебания с большей амплитудой (синяя линия) оказывается меньше, чем у колебания с малой амплитудой (оранжевая линия). Это служит еще одним подтверждением того, что нелинейные колебания не являются гармоническими.

Ну и напоследок: это всего лишь поверхностный экскурс в метод фазовых портретов, и словосочетание «на пальцах» попало в заголовок неспроста. Те же, кто решит углубиться в перипетии данного предмета, увидят, что за фазовыми портретами скрывается намного большее.

Видео:14. Дифференциальные уравнения второго порядка, допускающие понижение порядкаСкачать

Фазовый портрет уравнения второго порядка

ИССЛЕДОВАНИЕ УСТОЙЧИВОСТИ СТАЦИОНАРНЫХ СОСТОЯНИЙ НЕЛИНЕЙНЫХ СИСТЕМ ВТОРОГО ПОРЯДКА

Метод Ляпунова линеаризации систем в окрестности стационарного состояния. Примеры исследования устойчивости стационарных состояний моделей биологических систем. Уравнения Лотки. Уравнения Вольтерра. Метод функции Ляпунова

Пусть биологическая система описывается системой двух автономных дифференциальных уравнений второго порядка общего вида:

(5.1)

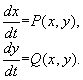
Стационарные значения переменных системы определяются из алгебраических уравнений:

(5.2)

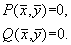
Стационарные состояния соответствуют особым точкам дифференциального уравнения первого порядка, определяющего интегральные кривые:

(5.3)

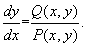
Математический анализ поведения траекторий этой системы на фазовой плоскости связан с именами французского математика Анри Пуанкаре и русского математика и механика Александра Михайловича Ляпунова (1857-1918).

Ляпунов показал, что в большом числе случаев анализ устойчивости стационарного состояния нелинейной системы можно заменить анализом устойчивости системы, линеаризованной в окрестности стационарного состояния.

Рассмотрим характер поведения переменных при некотором небольшом отклонении системы от состояния равновесия. Введем вместо переменных x, y новые независимые переменные x , h , определив их как смещения относительно равновесных значений переменных

(5.4)

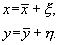
Подставив эти выражения в (5.1), получим:

(5.5)

, так как — координаты особой точки.

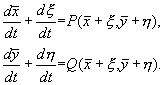
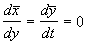
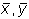
Предположим, что функции P и Q непрерывны и имеют непрерывные производные не ниже первого порядка. Тогда мы можем разложить правые части уравнений (5.5) в ряд Тейлора по переменным x , h .

(5.6)

(5.7)

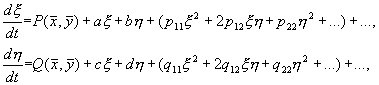
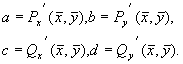
Учтем, что по определению особой точки

и отбросим в уравнениях (5.6) нелинейные члены. Получим систему линейных уравнений с постоянными коэффициентами — систему первого приближения:

(5.8)

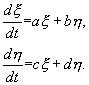
Решение этой системы было рассмотрено в Лекции 4. Оно определяется корнями характеристического уравнения системы:

(5.9)

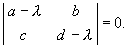
Ляпунов показал, что в случае, если оба корня уравнения (5.9):

(5.10)

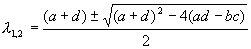
имеют отличные от нуля действительные части, исследование уравнений первого приближения (5.8) всегда дает правильный ответ на вопрос о типе устойчивости состояния равновесия в системе (5.1). А именно:

· если оба корня имеют отрицательную действительную часть и, следовательно, все решения уравнений первого приближения (5.8) затухают, то состояние равновесия устойчиво;

· если хотя бы один корень имеет положительную действительную часть, то есть система (5.8) имеет нарастающие решения, то состояние равновесия неустойчиво.

Если действительные части обоих корней характеристического уравнения равны нулю или если один корень равен нулю, а другой отрицателен, то уравнения (5.8) не дают ответа на вопрос об устойчивости состояния равновесия, и необходимо рассматривать члены более высокого порядка малости в разложении в ряд Тейлора правых частей уравнений (5.6).

В случае, когда оба корня характеристического уравнения имеют отличные от нуля действительные части ( грубые с истемы), уравнение первого приближения определяют не только устойчивость стационарного состояния, но и характер фазовых траекторий в достаточно малой его окрестности.

Как и в случае линейных уравнений (Лекция 4) здесь возможны пять типов грубых состояний равновесия: устойчивый узел, неустойчивый узел, устойчивый фокус, неустойчивый фокус и седло. Для исследования типов состояний равновесий удобно пользоваться диаграммой, изображенной на рис. 4.11. Для системы (5.1):

, (5.11)

. (5.12)

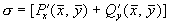
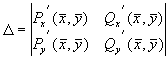
Грубым состояниям равновесия соответствуют все точки плоскости параметров s , D , лежащие вне оси D =0 и полуоси s =0, D >0.

Точкам оси D = 0 и полуоси s = 0, D >0 соответствуют негрубые состояния равновесия (негрубые особые точки). Их свойства могут быть изменены сколь угодно малыми изменениями правых частей уравнений (5.1) за счет сколь угодно малых изменений функций P(x,y), Q(x,y) и их производных. Поэтому характер негрубых состояний равновесия (в частности, устойчивость) уже не определяется значениями коэффициентов в правых частях уравнений первого приближения (5.8). В отличие от линейных систем, уже при небольших изменений в правых частях содержащихся там нелинейных членов может произойти качественное изменение фазового портрета — бифуркация.

1. Кинетические уравнения Лотки ( A . J . Lotka . Elements of Physical Biology, 1925)

Лоткой была исследована гипотетическая химическая реакция:

Модель очень простая и служит хорошей иллюстрацией применения исследования устойчивости стационарного состояния системы методом линеаризации.

Пусть в некотором объеме находится в избытке вещество А. Молекулы А с некоторой постоянной скоростью 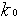превращаются в молекулы вещества X (реакция нулевого порядка). Вещество X может превращаться в вещество Y, причем скорость этой реакции тем больше, чем больше концентрация вещества Y – реакция второго порядка. В схеме это отражено обратной стрелкой над символом Y. Молекулы Y в свою очередь необратимо распадаются, в результате образуется вещество B (реакция первого порядка).

Запишем систему уравнений, описывающих реакцию:

(5.13)

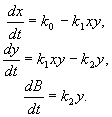
Здесь x , y , B — концентрации химических компонентов. Первые два уравнения этой системы не зависят от B , поэтому их можно рассматривать отдельно. Рассмотрим стационарное решение системы:

Из этих условий получим систему алгебраических уравнений, связывающих равновесные концентрации :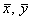

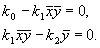
(5.14)

Координаты особой точки:

.

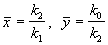
Исследуем устойчивость этого стационарного состояния методом Ляпунова. Введем новые переменные x , h , характеризующие отклонения переменных от равновесных концентраций :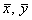

.

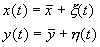
Линеаризованная система в новых переменных имеет вид:

(5.15)

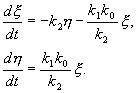
Отметим, что величины отклонений от стационарных значений переменных x , h могут менять знак, в то время как исходные переменные x , y , являющиеся концентрациями, могут быть только положительными.

Запишем характеристическое уравнение системы (4.3):

.

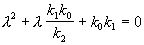
Корни характеристического уравнения:

.

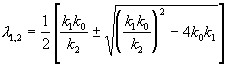
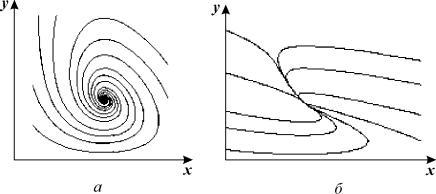
Фазовый портрет системы (5.13) изображен на рис. 5.1.

Рис. 5.1. Фазовый портрет системы 5.13.

а – устойчивый фокус ,

б – устойчивый узел.

При 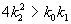подкоренное выражение отрицательно, и особая точка – фокус, при обратном соотношении – узел. И в том и в другом случае особая точка устойчива, так как действительная часть обоих корней характеристического уравнения отрицательна.

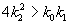
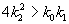
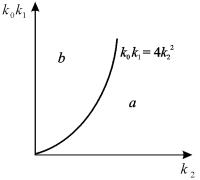
Таким образом, в описанной выше химической реакции возможны разные режимы изменения переменных в зависимости от соотношения величин констант скоростей. Если , имеют место затухающие колебания концентраций компонентов, при – бесколебательное приближение концентраций к стационарным.

Рис. 5.2 Плоскость параметров для системы 5.14.

а – область устойчивого фокуса; б – область устойчивого узла

Соотношение параметров 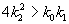соответствует изменению типа особой точки системы уравнений (5.13).

Рассмотрим плоскость параметров, где по оси абсцисс отложены значения константы k₂, а по оси ординат – произведение k ₀ k ₁ . Парабола k ₀ k ₁ = 4 k 2 ₂ делит изображенную на рис. 5.2 плоскость параметров на две области – устойчивых узлов и устойчивых фокусов. Задавая те или иные значения параметров, можно получить колебательный и бесколебательный режимы изменения концентраций веществ x и y , и фазовый портрет системы, соответственно, будет собой представлять фокус (а) или узел (б), изображенные соответственно на рис 5.1 а, и 5.1 б.

Если в системе установятся стационарные концентрации веществ x и y , это приведет к установлению постоянной скорости прироста концентрации вещества В в третьем уравнении системы (5.13):

.

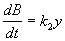
Ясно, что в действительности такая система реализоваться не может, так как в ней при t ® ¥ концентрация вещества В стремится к бесконечности. Однако система, подобная системе реакций Лотки, может представлять собой фрагмент более сложной химической системы. Исследованные нами уравнения правильно описывают поведение компонентов x и y , если приток вещества x (скорость его постоянна и равна k ₀ ) осуществляется из большого «резервуара», а отток вещества y – в большой «резервуар» (значение В очень велико). При этих предположениях на малых промежутках времени (по сравнению с временем существенного изменения заполненности емкости B ) наше рассмотрение является вполне правомерным.

2. Модель Вольтерра

В качестве второго примера рассмотрим классическую модель взаимодействия видов, которая впервые была предложена В. Вольтерра в тридцатые годы XX века для объяснения периодических изменений числа особей, так называемую вольтерровскую модель «хищник-жертва». Более подробно модели взаимодействия видов мы рассмотрим в Лекции 9.

Пусть в некотором замкнутом районе живут хищники и жертвы, например, зайцы и волки. Зайцы питаются растительной пищей, имеющейся всегда в достаточном количестве. Волки могут питаться лишь зайцами. Обозначим число зайцев (жертв) x, а число волков (хищников) – y . Так как количество пищи у зайцев неограниченно, мы можем предположить, что они размножаются со скоростью, пропорциональной их числу:

(5.16)

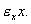
Если рождаемость зайцев превышает их смертность, e > 0. Выражение (5.16) соответствует автокаталитической реакции первого порядка.

Пусть убыль зайцев пропорциональна вероятности встречи зайца с волком, т.е. пропорциональна произведению численностей xy . Можно предположить по аналогии с бимолекулярными реакциями, где вероятность появления новой молекулы пропорциональна вероятности встречи двух молекул, что и количество волков нарастает тем быстрее, чем чаще происходят их встречи с зайцами, а именно, пропорционально xy .

Кроме того, имеет место процесс естественной смертности волков, причем скорость смертности пропорциональна их количеству.

Эти рассуждения приводят к системе уравнений для изменений численности зайцев-жертв x и волков-хищников y.

(5.17)

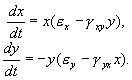
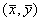
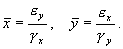
Покажем, что система уравнений (5.17) имеет на фазовой плоскости переменных xy ненулевую особую точку типа центр. Координаты этой особой точки легко найти, приравняв правые части уравнений системы (5.17) нулю. Это дает стационарные ненулевые значения:

.

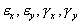
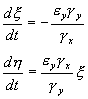
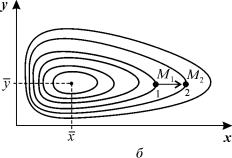
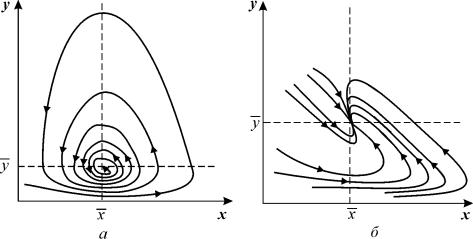
Так как все параметры положительны, точка расположена в положительном квадранте фазовой плоскости. Линеаризация системы вблизи этой точки дает:

(5.18)

Рис. 5.3. Фазовый портрет системы 5.17. Особая точка типа «центр».

а – параметры системы: e _x = 4, g _xy = 0,3, e _y = g _yx = 0,4

б – параметры системы: e _x =2, g _xy = 0,3, e _y = g _yx = 0,4

Здесь x , h — отклонения 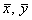численностей от их стационарных значений:

Характеристическое уравнение системы (5.18):

Корни этого уравнения чисто мнимые:

.

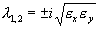
Таким образом, исследование системы показывает, что траектории вблизи особой точки являются концентрическими эллипсами, а сама особая точка – центром. Рас c матриваемая модель Вольтерра и вдали от особой точки имеет замкнутые траектории, хотя форма этих траекторий уже отличается от эллипсоидальной, и определяется параметрами системы (рис. 5.3).

Изменения численности жертвы и хищника во времени представляют собой колебания, причем колебания численности хищника отстают по фазе от колебаний жертв.

Как мы уже отмечали в Лекции 4, особая точка типа центр устойчива по Ляпунову, но не асимптотически. Покажем на данном примере, в чем это проявляется. Пусть колебания x ( t ) и y ( t ) происходят таким образом, что изображающая точка движется по фазовой траектории 1 (рис 5.3).

В момент, когда точка находится в положении М₁, в систему добавляется извне некоторое число особей y такое, что изображающая точка переходит скачком из точки M ₁ в точку M ₂ . Если после этого систему предоставить самой себе, колебания x ( t ) , y ( t ) уже будут происходить с большими амплитудами, чем прежде, и изображающая точка будет двигаться по траектории 2. Это и означает, что колебания в системе неустойчивы: они навсегда изменяют свои характеристики при внешнем воздействии.

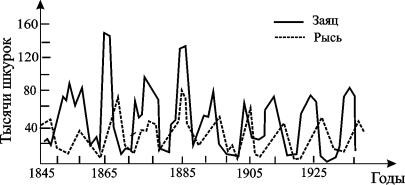
Рис. 5.4. Кривые численности зайца и рыси в Канаде

(по К. Вилли, В. Детье, 1974)

В дальнейшем мы рассмотрим модели, описывающие устойчивые колебательные режимы, и покажем, что на фазовой плоскости такие асимптотически устойчивые периодические движения описываются предельными циклами.

На рис. 5.4 кривые колебаний численности пушных зверей по данным компании Гудзонова залива о числе заготовленных шкурок. Во всех классических учебниках в течение многих лет колебательный характер этих изменений приводили как подтверждение гипотез, положенных в основу модели Вольтерра, которую мы только что рассмотрели. Действительно, периоды колебаний численности зайцев (жертв) и рысей (хищников) примерно одинаковы и составляют порядка 9 – 10 лет. При этом максимум численности зайцев опережает, как правило, максимум численности рысей на один год. Можно полагать, что мы видим регулярные колебания, осложненные случайными факторами, связанными с погодой и проч.

Однако возможна и другая интерпретация этих данных наблюдений на основе моделей детерминированного хаоса. О дискретных моделях такого типа мы уже говорили в Лекции 3. Непрерывные модели популяционной динамики, приводящие к детерминированному хаосу, мы рассмотрим в Лекции 9.

Серьезным недостатком рассмотренной модели Вольтерра является неустойчивость решений по отношению к малым случайным воздействиям, приводящим к изменению переменных. Кроме того, в силу «негрубости» этой системы произвольно малое изменение вида правых частей уравнений (величин параметров системы) приведет к изменению типа особой точки, и, следовательно, к изменению характера фазовых траекторий.

Поскольку природные системы подвергаются огромному количеству случайных воздействий, реалистическая модель должна быть по отношению к ним устойчивой. Поэтому негрубые системы не могут давать адекватное описание природных явлений.

Различные модификации рассмотренной нами системы, изученные самим Вольтерра и другими авторами, лишены этих недостатков. Наиболее широко известные из них будут рассмотрены в Лекции 9. Здесь мы остановимся на модели, которая учитывает самоограничение в росте обеих популяций. На ее примере видно, как может меняться характер решений при изменении параметров системы.

Итак, рассмотрим систему:

(5.19)

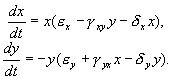
Система (5.19) отличается от ранее рассмотренной системы наличием в правых частях членов:

Эти члены отражают тот факт, что численность популяции жертв не может расти до бесконечности даже в отсутствие хищников в силу ограниченности пищевых ресурсов, ареала существования и проч. Такие же «самоограничения» накладываются на популяцию хищников.

Система имеет два стационарных решения: нулевое и ненулевое. Анализ показывает, что нулевое решение представляет собой неустойчивый узел. Рассмотрим систему алгебраических уравнений, решение которых дает координаты ненулевого стационарного состояния.

( 5 .20)

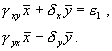
Корни характеристического уравнения системы, линеаризованной в окрестности особой точки:

.

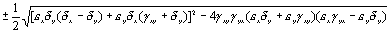
Из выражения для характеристических чисел видно, что если выполнено условие

то численности хищников и жертв совершают во времени затухающие колебания. Система имеет особую точку – устойчивый фокус.

Рис. 5.5. Фазовый портрет системы 5.19

а – устойчивый фокус,

б – устойчивый узел,

При изменении знака неравенства на обратный точка становится устойчивым узлом.

И в том и в другом случае стационарное состояние асимптотически устойчиво, и решение устойчиво к малым изменениям правых частей уравнений. Таким образом, самоограничение популяции приводит к устойчивости ее численности.

Важно отметить, что простейшие вольтерровские модели, которые мы рассмотрели, не могут описывать устойчивые колебания с постоянными периодом и амплитудой. Для описания таких колебаний необходимы нелинейные модели, имеющие на фазовой плоскости предельный цикл . Они будут рассмотрены в Лекции 8.

МЕТОД ФУНКЦИЙ ЛЯПУНОВА ИССЛЕДОВАНИЯ УСТОЙЧИВОСТИ СТАЦИОНАРНОГО СОСТОЯНИЯ.

При аналитическом исследовании устойчивости стационарного состояния часто используется метод подбора функции, линии уровня которой представляют собой замкнутые траектории – «ловушки» для фазовых траекторий системы типа (5.1)

Этот метод применим к автономной системе уравнений n -го порядка

(5.21)

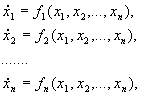
Он состоит в непосредственном исследовании устойчивости ее стационарного состояния при помощи подходящим образом подобранной функции Ляпунова .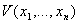

Метод основан на двух теоремах.

Если существует дифференцируемая функция V ( x ₁ ,…, x_n ), удовлетворяющая в окрестности начала координат следующим условиям:

б)

причем 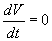лишь при x ₁ = … = x_n = 0 ,

то точка покоя системы (5.21) устойчива.

Если существует дифференцируемая функция V ( x ₁ ,…, x_n ), удовлетворяющая в окрестности начала координат следующим условиям:

a ) V ( x ₁ ,…, x_n ) = 0 и сколь угодно близко от начала координат имеются точки, в которых V ( x ₁ ,…, x_n ) > 0;

б)

причем 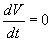лишь при x ₁ =…= x_n = 0,

то точка покоя системы (5.21) неустойчива.

С доказательством этих теорем можно познакомиться в книге Л.Э. Эльсгольц «Теория дифференциальных уравнений» или в других учебниках по теории дифференциальных уравнений.

Общего методы построения функции Ляпунова не существует. Однако для линейных автономных систем ее следует искать в виде:

и т.п., подбирая надлежащим образом коэффициенты a > 0 , b > 0. Для нелинейных систем a и b могут быть произвольных знаков.

1. Рассмотрим линейную систему:

Выберем функцию Ляпунова: V = x 2 + y 2 . Тогда

Это выражение всегда отрицательно при х ¹ 0 , т.к. в скобках стоят четные степени x . Следовательно, точка (0, 0) устойчива.

2. Рассмотрим систему уравнений, описывающую конкуренцию видов, численности которых x и y . Каждый из видов размножается в соответствии с логистическим законом, а при встрече (произведения в правых частях уравнений), численность как одного, так и другого вида уменьшается.

(5.22)

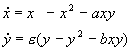
Исследуем стационарное состояние, соответствующее сосуществованию видов ( ` x , ` y ) – ненулевое для x и y . Его координаты:

. (5.23)

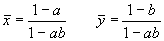
В. Вольтерра показал, что стационарное состояние (5.23) устойчиво для параметров системы a > 0, b £ 1 , построив функцию Ляпунова:

.

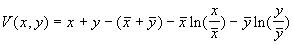
Ее производная равна

и отрицательна при малых значениях коэффициентов a , b и x , y > 0. Доказательство приведено в книге В. Вольтерра. «Математическая теория борьбы за существование» (М., 1976)

Ризниченко Г.Ю., Рубин А.Б. Математические модели биологических продукционных процессов. М., изд. МГУ, 1993

Вольтерра В. Математическая теория борьбы за существование М., Наука, 1976

Эльсгольц Л.Э. Теория дифференциальных уравнений. М., Наука, 1971

🎦 Видео

Асташова И. В. - Дифференциальные уравнения. Часть 2 - Фазовый портретСкачать

Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

Линейное дифференциальное уравнение Коши-ЭйлераСкачать

ТАУ. Matlab/SIMULINK Фазовые портреты систем нелинейных диф. уравненийСкачать

Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентамиСкачать

Кулешов А. С. - Теоретическая механика. Семинары - Фазовые портретыСкачать

Решение систем уравнений второго порядка. 8 класс.Скачать

Кривые второго порядкаСкачать

ТАУ. Matlab/SIMULINK Фазовые портреты нелинейных и линейных диф. уравненийСкачать

ЛОДУ 2 порядка c постоянными коэффициентамиСкачать

Как распознать талантливого математикаСкачать

16. Линейные неоднородные дифференциальные уравнения 2-го порядка с постоянными коэффициентамиСкачать

15. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентамиСкачать

Задача Коши ➜ Частное решение линейного однородного дифференциального уравненияСкачать

Линейное однородное дифференциальное уравнение 2-го порядка с постоянными коэффициентами.Скачать

Дифференциальные уравнения, 7 урок, Дифференциальные уравнения, допускающие понижение порядкаСкачать