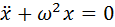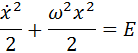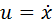Фазовый портрет системы дифференциальных уравнений online (2 видео)

Фазовые портреты «на пальцах» или что можно узнать о решениях диффура, не решая его

Очень часто в ряде наук встречается ситуация, когда модель рассматриваемого процесса сводится к дифференциальному уравнению. Причём, в большинстве реальных задач это уравнение довольно сложно решить, или совсем невозможно. И вот тут в полный голос звучит извечный вопрос: как быть?

Встречайте: фазовые портреты (они же фазовые диаграммы). Простым языком, фазовый портрет — это то, как величины, описывающие состояние системы (a.k.a. динамические переменные), зависят друг от друга. В случае механического движения это координата и скорость, в электричестве это заряд и ток, в известной популяционной задаче это количество хищников и жертв и т.д.

Чем хороши фазовые портреты? А тем, что их можно построить не решая динамические уравнения системы. В некоторых случаях построение фазового портрета становится совсем простой задачей. Однако, одновременно с этим, фазовые портреты дают вдумчивому наблюдателю очень много информации о поведении системы.

Начнём с простого примера — малых колебаний (так же называемых гармоническими). Малые колебания встречаются почти в каждой сфере естественных наук. Для определённости, будем рассматривать колебания металлического стержня, подвешенного за один из концов (частный случай так называемого физического маятника). Можно показать, что его колебания описываются следующим дифференциальным уравнением:

Где x — угол отклонения стержня от вертикали, точка над x означает производную по времени, а коэффициент перед синусом зависит от размера и массы стержня.

Если амплитуда (размах) колебаний достаточно мала, синус можно приближенно заменить его аргументом (вы ведь помните первый замечательный предел, нет?). В таком случае, уравнение принимает следующий вид:

Это уравнение легко решается регулярными методами, но, давайте, попробуем применить к нему метод фазовых портретов. Для этого, домножим уравнение на производную и проинтегрируем его один раз по времени:

Получилось выражение, первый член которого выглядит как кинетическая энергия. Это не случайно — на самом деле мы получили именно закон сохранения энергии. Постоянная Е в правой части (полная энергия системы на единицу массы) может принимать различные значения, которые соответствуют разным начальным состояниям системы.

Полученный нами закон сохранения превратился в уравнение кривой на плоскости (x,u):

Для разных значений Е мы получим разные кривые. Нарисуем несколько таких линий для разных значений энергии:

По горизонтальной оси отложена величина x, по вертикальной — u

Каждая из полученных линий называется фазовой траекторией. Когда меняется состояние системы, изображающая её точка движется по одной из этих траекторий, стрелки указывают направление движения изображающей точки.

По графику видно, что значения скорости и координаты меняются циклическим образом, то есть периодически повторяются. Отсюда можно сделать вывод, что описываемая рассмотренным уравнением система будет совершать колебания. Бинго! Именно так ведёт себя маятник, и если решить уравнение, решение будет иметь вид периодических функций (а именно — комбинации синуса и косинуса).

Следует однако помнить, что замена синуса его аргументом оправдана лишь для малых углов отклонения (от 10 градусов и меньше), поэтому мы не можем доверять тем траекториям, которые выходят за границы области, ограниченной жирными пунктирными линиями, то есть из четырех приведенных траекторий лишь оранжевая достоверно отображает реальность. Кроме того, поскольку x это угол, то его значения, соответствующие 180 и -180 градусам описывают одно и то же положение стержня, то есть правая и левая пунктирные линии (тонкие) на графике это на самом деле одна и та же линия.

Теперь, поскольку нам понятна суть, можно перейти к чему-то посложнее. Выше мы очень сильно упростили уравнение и при этом ограничили себя только малыми колебаниями. Математик бы сказал, что мы линеаризовали уравнение и пренебрегли нелинейными эффектами. Так давайте включим в рассмотрение нелинейность. Вернёмся к самому первому уравнению — с синусом. Если мы повторим с ним то, что проделали с линейным уравнением, мы получим следующий закон сохранения:

В зависимости от значения энергии, мы опять получаем разные кривые, которые приведены на следующем рисунке, причем выбраны те же значения энергии, что и на первой диаграмме, и те же цвета для линий.

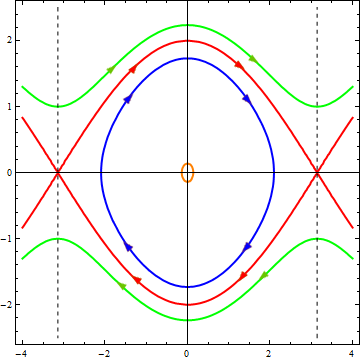
По горизонтальной оси отложена величина x, по вертикальной — u

Как видите, процессы происходящее в системе стали более разнообразными:

При малых энергиях (оранжевая и синяя траектории) существует колебательный режим, но колебания уже не являются гармоническими — фазовые траектории уже не имеют форму эллипсов.

При больших энергиях (зеленая траектория) колебаний уже нет, вместо этого мы получаем вращательное движение с переменной скоростью. И действительно, если достаточно сильно «толкнуть» стержень, он будет вращаться, замедляясь при подъёме и ускоряясь при спуске.

При определенном промежуточном значении энергии получается особый набор траекторий, которые отделяют друг от друга области соответствующие разным типам движения и поэтому называются сепаратрисами. И да, значение энергии для красной кривой было выбрано мной именно так, чтобы в нелинейном случае получилась сепаратриса. Каждая ветвь сепаратрисы это траектория, соответствующая особому типу движения. Посмотрим на диаграмму: движение начинается с очень маленькой скоростью от одного крайнего положения стержня, при приближении к положению равновесия скорость растёт, а после изображающая точка все более замедляясь уходит к крайнему положению, где и останавливается. Это соответствует тому, что мы поднимаем стержень вертикально вверх и отпускаем его, проносясь через положение равновесия он поднимается к верхней точке с другой стороны и останавливается.

А теперь давайте посмотрим насколько близки к истине наши выводы, сделанные на основе фазовых портретов. Перед вами график решения линейного уравнения:

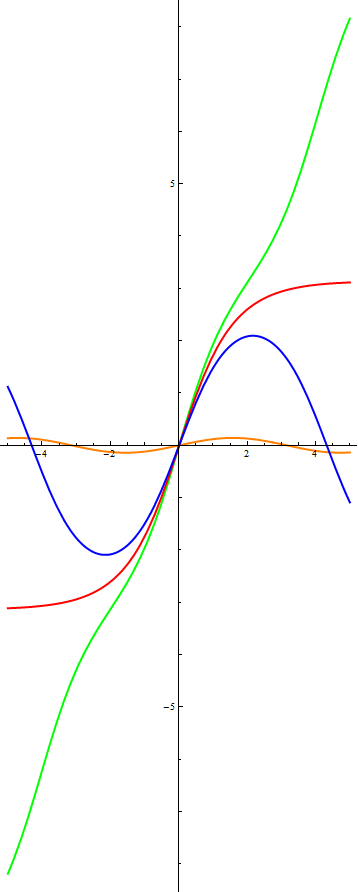
По горизонтальной оси отложено время, по вертикальной — x

Цветовая маркировка на этих графиках такая же, как и на фазовых портретах. Судить о том, насколько верные выводы были сделаны на основе фазовых портретов я предоставлю вам, дорогие читатели. Обращу ваше внимание только на один момент — колебания в линейном случае происходят синхронно — с одной и той же частотой. В нелинейном же случае, частота колебания с большей амплитудой (синяя линия) оказывается меньше, чем у колебания с малой амплитудой (оранжевая линия). Это служит еще одним подтверждением того, что нелинейные колебания не являются гармоническими.

Ну и напоследок: это всего лишь поверхностный экскурс в метод фазовых портретов, и словосочетание «на пальцах» попало в заголовок неспроста. Те же, кто решит углубиться в перипетии данного предмета, увидят, что за фазовыми портретами скрывается намного большее.

Содержание

Фазовые портреты линейных систем
Фазовые портреты линейных систем
Построение фазового портрета в 2D и 3D в Xcos
Двумерный фазовый портрет в Xcos
Построение трёхмерного графика в Xcos
Построение 3D графика с помощью контекста в Xcos
📺 Видео

Видео:Асташова И. В. - Дифференциальные уравнения. Часть 2 - Фазовый портретСкачать

Фазовые портреты линейных систем

Видео:Решение дифференциальных уравнений. Построение фазового портрета систему ДУ. Урок 47Скачать

Фазовые портреты линейных систем

На этом этапе рассмотрим фазовую траекторию и фазовый портрет линейной системы. При решении задач построения фазового портрета в линейных системах необходимо соблюдать следующую последовательность действий. Выберите систему координат так, чтобы ее начальная точка совпадала с положением равновесия системы. Создайте дифференциальное уравнение движения.

Исключить из уравнения время и интегрировать дифференциальные уравнения полученных фазовых траекторий для нахождения зависимости между отклонением системы обобщенными координатами и ее обобщенной скоростью. 4 построить интегральную кривую на фазовой плоскости при различных начальных условиях движения и найти фазовый портрет системы. 5 фазовый портрет определяет характер движения и равновесия системы. Задача 20.16.Создайте фазовый портрет гармонического генератора без затухания. Solution.

Определить закон вынужденных крутильных колебаний твердого тела, если его момент инерции относительно оси г, направленной вдоль проволоки, равен Л,. Людмила Фирмаль

Гармонические не ослабляющие осцилляторы, действие восстанавливающей силы, пропорциональное отклонению системы от ее равновесного положения, вызывают колебания, называемые свободой, и всегда стремятся вернуть систему в равновесное положение. Примеры гармонических неуплотняющих генераторов включают подпружиненную нагрузку, математический и физический маятник с малым углом отклонения который не учитывает сопротивление и электрический генератор, который состоит из емкости и индуктивности, но не имеет сопротивления.

Во всех этих случаях вид дифференциальных уравнений движения имеет вид X A x 0, 1 Где x-отклонение системы от положения равновесия или заряд электрического колебательного контура см. Главу 8, A s t-нагрузка, приложенная к пружине c-коэффициент жесткости, t-масса, длина маятника, сила тяжести, k Pa физическое ускорение где Pa —вес маятника, a —вес подвески, а —момент, л2 1 CB-для электрического колебательного контура I-индуктивность, C-емкость. Похлопывание Уравнение 1 в виде системы Если вы исключите время из этой системы, вы найдете yu k x yh y.

Единственной специальной точкой этого дифференциального уравнения является положение равновесия, когда правая часть 2 становится неопределенной, начало координат x 0 и y 0.При разделении переменной у Ю-На х ых. 3 Когда вы интегрируете 4 Где C — любая постоянная интегрирования, определяемая начальными условиями движения. Уравнение 4 представляет собой фазовый портрет системы. Это семейство эллипсов см. рис.20.3 симметрично относительно сингулярности симметрии.

Каждый эллипс-это фазовая орбита. Сингулярность центр определяется из 4 как эллипс, вырождающийся в точку при начальных условиях, соответствующих C 0. Какие эллипсы соответствуют периодическому движению системы Его параметры зависят только от начальных условий движения. Если задано начальное условие, то точка изображения представляет собой тот же эллипс, что и при перемещении по всему изображению. system. So, каждая из интегральных кривых в этом случае является всей фазовой траекторией.

Период колебаний не зависит от начальных условий движения. Поэтому любые эллипсы, представляющие точки, записываются со скоростью YЛ В то же время, идите по часовой стрелке. Отметим, что уравнение 4, в то же время, является законом сохранения механической энергии движения и потенциала рассматриваемой консервативной системы. Задача 20.17.Найти фазовый портрет гармонического датчика вязкого трения. Solution. In гармонические осцилляторы с вязким трением, сопротивление вязкое трение, электрическое сопротивление добавляется к восстанавливающей силе. Это пропорционально скорости и первой скорости в противоположном направлении.

Учитывая сопротивление, дифференциальное уравнение движения системы выглядит следующим образом X 2lL4-A x 0, 1 Где 2n a a, a — коэффициент пропорциональности сопротивления YaL — aL. Величина n имеет то же измерение, что и k, т. е. с-1, Если время измеряется в seconds. As перед тем, как представить I y, перепишем уравнение 1 в виде системы из 2 уравнений 2 Ах 3 Если исключить время из этой системы — 2pu-к X г 4 Итак, сингулярность координатного уравнения — это положение равновесия, а неопределенность справа равна 0 0. 4 является началом нарисованного part. To разделите переменные в выражении 4, внесите изменения.

Уравнение 4 принимает вид г-ых гг х-ый 2стр к. Интегрирование этого уравнения зависит от типа корня многочлена, возведенного в квадрат знаменателя с правой стороны. Поэтому рассмотрим отдельно 2 случая n k — для низкого сопротивления и n k-для высокого resistance. It также примыкает к граничному случаю n-K. Для низкого уровня resistance. In в этом случае при n k форма Интеграла 5 имеет вид Х4-2ld а 2 с ехр — — а С18, б Где AA2 — I2, C-произвольная интегральная константа.

Возвращаясь к старой переменной, т. е. r y заменяя x, находим уравнение интегральной кривой У2 2ll a2l по-2-с ехр АГС е х 7 Полученное уравнение интегральной кривой становится более заметным при переходе к новой переменной. Новая переменная становится новой декартовой координатой. После преобразования У2 2 л. ху k2×2 г ЛК 2 kgx2 Х2 y2 7 вместо С1 ехр 2 — — АГС г — -. 8 Введем полярные P и p. Х1 pCO8f, У1 p51n п. Уравнение 8 принимает вид Р схема ГФ. 9 Направление движения точки визуализации рис.

А соответствует движению по часовой стрелке. Угол Р отсчитывается в противоположном направлении. Таким образом, в уравнении 9, угол Р непрерывно уменьшается. Это означает, что радиус-вектор точки изображения p также уменьшается бесконечно. Интегральная кривая-закручивающаяся спираль рисунок а, наматывающаяся к началу координат. Каждая интегральная кривая в этом случае является фазовой траекторией. Абсолютное значение фазовой скорости остается неизменным. o V x2 2 V y2 2 Lu k2×2.

Поскольку фазовая скорость бесконечно уменьшается по мере приближения точки визуализации к ее равновесному положению, точка визуализации не может достичь начала координат за ее пределами. Выпуск 20.1-7 к. Время, но приближается асимптотически. Сингулярность в этом случае называется стационарным фокусом. В начальных условиях точки изображения стремятся к началу координат, поэтому равновесие системы, соответствующей началу координат, стабилизируется.

Так как требуется определить только вынужденные крутильные колебания шара, то решение задачи сводится к отысканию частного решения уравнения (1). Людмила Фирмаль

Линейное преобразование x1 A1x, A 5 xx не изменяет характер интегрирования curve. In дело в том, что если значения p k1 на плоскости спирали малы, то они близки к окружности Этот круг превращается в эллипс с небольшим значением n C при возврате к исходной переменной У2- — 2phu — — k2×2 со Таким образом, в плоскости xy спираль фазового локуса ближе к этому эллипсу рисунок B. Определите шаг спирали рисунок а. Из диаграммы видно, что шаг спирали равен xn-xn 1.С другой стороны, как известно, решение исходного дифференциального уравнения 1 имеет вид х ае-Р п А8- — — 11 Здесь воздух определяется начальными условиями движения.

Период колебаний равен t 2l Шаг спирали будет равен хп-ху 1 А-А- М А 1-е- для nT 1 уравнение 13 может быть приблизительно представлено расширением набора функций. 1-й- 1- 1-л — — … 12 13 Тогда шаг представляется приближенной формулой хп — хп 1 Апт. Поэтому в nT 1 шаг спирали пропорционален логарифмическому уменьшению. Если сопротивление большое. если мы интегрируем уравнение 5 для n k и введем полученный результат читать и находить г За — — 2яу4-АХА 14 Правая часть этого уравнения легко учитывается следующим образом y2 2n xy kgx y nxy- n-A8×2 — y b2x y b x , введите обозначение, чтобы сделать его кратким Б н-уя — К2,б н уя — к.

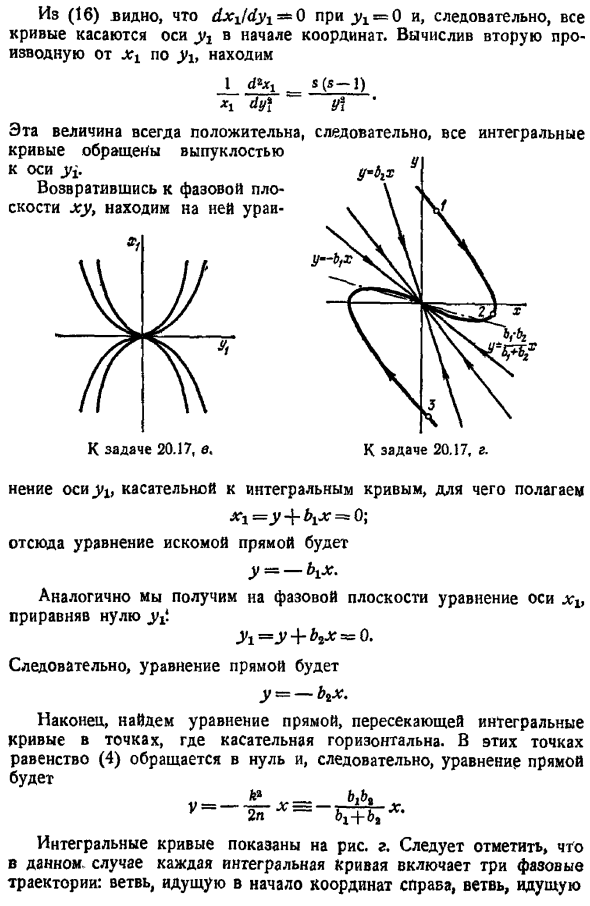
Уравнение 14 можно записать в виде Су с Су М 6 15 учитывая, что uy равно и равно ХХ г ВХ, ух г ВХ В качестве новой декартовой координаты уравнение 15, определяющее семейство интегральных кривых, принимает вид 16 где S г 6×1.Интегральная кривая показана на рисунке. С. 16 от LX СГР — O для x 0, поэтому все кривые находятся в контакте с осью Y1 в начале координат. если посчитать, то 2-я производная от Х в отношении г, Я Нет. 1 5 5-1 u и Это значение всегда положительное, и кривая выпуклая относительно оси y. Когда вы вернетесь на фазовую плоскость xy Выпуск 20.17, С. Поэтому все интегралы Выпуск 20.17, Г. 1 Y M изменение касательной оси yb к интегральной кривой, задающей M 0.

Отсюда уравнение искомой линии выглядит так — M- Аналогично получаем уравнения оси Х на фазовой плоскости. L 3 M 0- Таким образом, уравнение линии является у — ВХ. Наконец, найдите уравнение для линии, которая пересекает кривую интегрирования в точке, где касательная равна horizontal. At в этих точках уравнение 4 исчезает, и поэтому уравнение прямой выглядит так Год — б б 2Н 6, х Интегральная кривая показана на рисунке. d. обратите внимание, что в этом случае каждая кривая интегрирования содержит 3 фазовых локуса ветви к правому началу координат, ветви к левому началу координат и singularity.

В этом случае по всем фазовым траекториям точка изображения перемещается к началу координат и от сингулярного узла к стабильному узлу. Характер апериодического движения, осуществляемого исходной механической системой, легко определяется расположением точек изображения на фазовой траектории. Если точка визуализации в первый момент находится в положении, то ее скорость изначально положительна, и расстояние от положения равновесия системы визуализации увеличивается до тех пор, пока точка визуализации не пересечет ось dg. Тогда скорость будет отрицательной, и начальная система окажется асимптотически близкой к положению равновесия.

Если в первый момент точка изображения находится в положении 2, исходная система будет двигаться асимптотически Восемь х ст г- tG СТ Р Т с с Положение равновесия, поскольку отклонение системы является положительным, а скорость направлена в отрицательное направление оси X. Задача 20.18.Тело, лежащее на горизонтальной, негладкой поверхности, прикреплено к стене пружиной рисунок а. Коэффициент жесткости пружины c, максимальное значение сушильной кулоновской силы трения R. сила трения при движении постоянна по абсолютной величине и направлена в противоположную сторону от скорости. Начало отсчета выбирается в конце пружины, которая не растягивается.

Тело в первый момент освободилось, переместившись на расстояние x0 Тири без начальной скорости. Найти уравнение движения тела, а в случае 0 12—построить зависящие от времени и фазы траектории перемещений. Решение. Создайте дифференциальное уравнение движения Тело ТЯ-Щ Р 1 Знак минус соответствует положительной проекции скорости и знак плюс соответствует отрицательной проекции скорости на оси X. Показано в П К П Д SOP81 И Максимальное отклонение тела, в котором сила трения уравновешивается реакцией пружины от положения, в котором пружина не растягивается. в этом случае выражение 1 можно записать в виде пг с с х Д О 2 Или х А х Д 0 Вот, Си м к. Поставил г.

А потом… — , А х Д Отсюда Ла х-Д 1х г Или после интеграции — — х Г С. 3 Для этого интеграла знак плюс соответствует Y-y 0 и минус-Y y 0. Предположим, что первый момент 0 имеет x x0 0,а Y y 0.Сразу после начала упражнения y-x 0, а в Формуле 3 Нужно взять знак минус. Найти уравнение окружности вокруг точки. V координата x D, y 0.in в случае x-x1 объект теряет скорость и движется вверх x y 0. в Формуле 3 необходимо использовать знак плюс. Получим уравнение окружности вокруг точки A1 — D, 0.Точка xy симметрична относительно L, x0, а точка xy симметрична относительно M, xg и так далее.

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

Видео:ТАУ. Matlab/SIMULINK Фазовые портреты систем нелинейных диф. уравненийСкачать

Построение фазового портрета в 2D и 3D в Xcos

Два подхода к построению фазового портрета на примере аттрактора Рёсслера

В представленных ранее примерах, мы рассмотрели вывод графической составляющей моделируемых систем двумя способами: с помощью осциллографов CMSCOPE и CSCOPE и путём задания контекста. Однако в обоих случаях графики строились в системах координат, где на горизонтальной оси откладывались временные отсчеты, а по вертикальной – значения функции в указанные моменты времени. И, хотя вопрос разложения дифференциальных уравнений на фазовые переменные был затронут в статье, не освещенным остался вопрос построения фазового портрета. Этой, столь полезной для анализа поведения решений моделируемых систем дифференциальных уравнений, процедуре и будет посвящён данный материал.

Мы рассмотрим два подхода к построению фазовых траекторий динамической системы на примере аттрактора Рёсслера. Данная система дифференциальных уравнений выбрана не случайно. Дело в том, что при моделировании системы Рёсслера, именно фазовый портрет представляет интерес, построение же интегральных кривых, как функций времени, не даёт полной картины происходящих в системе процессов.

Аттрактор Рёсслера — это хаотический аттрактор, которым обладает система дифференциальных уравнений Рёсслера вида:

При значениях параметров ( a=b=0.2 ) и ( 2.6 leq c leq 4.2 ) уравнения Рёсслера обладают устойчивым предельным циклом. При этих значениях параметров период и форма предельного цикла совершают последовательность удвоения периода.

Сразу же за точкой ( c=4.2 ) возникает явление хаотического аттрактора. Чётко определённые линии предельных циклов расплываются и заполняют фазовое пространство бесконечным счетным множеством траекторий, обладающим свойствами фрактала. Именно случай бесконечных самоповторяющихся траекторий мы и замоделируем.

Построим блок-схему системы (1), задав параметры в контексте со значениями ( a=b=0.1, с=14 ).

Для построения трёх уравнений системы (1) нам понадобятся блоки INTEGRAL_m, BIGSOM_f, PRODUCT, CONST и GAINBLK.

Видео:Дополнительные главы ИДУ: Построение фазовых портретов | Занятие 3Скачать

Двумерный фазовый портрет в Xcos

В рамках первого подхода к построению фазового портрета, воспользуемся
блоком , который располагается на палитре «Регистрирующие устройства» и осуществляет построение графика зависимости ( y(x) ), где ( x ) отвечает за значения по оси абсцисс, а значения ( y(x) )откладываются на оси ординат.

Приступим к построению блочной диаграммы Xcos.

1. Для начала, добавьте на рабочую область 3 блока интегратора INTEGRAL_m с нулевыми начальными значениями, 4 блока BIGSOM_f, блок умножения переменных PRODUCT и блоки для задания коэффициентов CONST и GAINBLK.

Расположите указанные блоки в порядке использования в уравнениях. В результате должна получиться заготовка, приближенная к изображённой на рис. 57.

Рисунок 57. Заготовка для создания блок-схемы системы (1)

2. На построении соединительных линий между блоками Xcos для первых двух уравнений системы Рёсслера не будем подобно останавливаться, так как оно представляется легко осуществимым на основе приобретённого читателем опыта. Результат установления связей для переменных ( y, x ) отображен на рис. 58.

Рисунок 58. Первые два уравнения системы (1)

3. Сбор блок-схемы третьего уравнения системы Рёсслера нужно начать со второго слагаемого, то есть осуществить произведение переменной ( z ) и скобки ( (x-c)), см. рис. 59.

Рисунок 59. Блок схема части третьего уравнения системы (1)

4. Осталось только подвести нужные соединительные линии на регулярные входы последнего сумматора и направить его выход на соответствующий интегратор, ( z ).

Результатом данных манипуляций будет схема, блок-изображённая на рис. 60.

Рисунок 60. Блок-схема системы Рёсслера трёх диф. уравнений

5. Далее, необходимо добавить блоки для осуществления моделирования CLOCK_c, END, проведя соединительные линии и настроив внутренние параметры блоков для моделирования на протяжении 300сек.

Для вывода фазовых траекторий, добавьте блок CSCOPXY, на регулярные входы которого направьте интересующие нас переменные ( y, x ) для вывода графика ( y(x) ), а на управляющий вход – соединительную линию от индикатора отсчетов CLOCK_c.

Обратите внимание, что названия входов блока CSCOPXY иллюстрируют построение функции ( y(x) ).

В результате блок-схема, реализующая построение траекторий аттрактора Рёсслера на фазовой плоскости примет вид, такой, как показано на рис. 61.

Рисунок 61. Блок-схема моделирования системы Рёсслера

Запустите моделирование на протяжении 300сек., настройте внутренние параметры блока CSCOPXY так, чтобы странный аттрактор хорошо вписывался бы в координатную сетку, как показано на рис. 62.

Рисунок 62. Аттрактор Рёсслера на фазовой плоскости

Итак, результатом моделирования бифуркаций аттрактора Рёсслера будет фазовая траектория ( y(x) ), иллюстрирующая сценарий перехода к хаосу через каскады бифуркаций удвоения периода Фейгенбаума, субгармонические каскады и гомоклинический каскад бифуркаций.

Видео:Дифференциальные уравнения 6. Фазовые траектории. Особые точки автономных системСкачать

Построение трёхмерного графика в Xcos

Для большей наглядности результата моделирования, заменим блок CSCOPXY блоком CSCOPXY3D.

Функциональный блок располагается на палитре «Регистрирующие устройства» и служит он для отображения трёхмерной системы координат, что становится понятно из его названия.

Изменённая часть блок-схемы и результат моделирования аттрактора Рёсслера представлены на рис. 63а,б.

Рисунок 63a.Моделирование 3D системы Рёсслера — добавление блока CSCOPXY3D в блок-схему

Рисунок 63б.Результат использования Xcos блока генерации трёхмерной сетки координат

Видео:18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать

Построение 3D графика с помощью контекста в Xcos

Рассмотрим ещё один способ построения фазового портрета систем дифференциальных уравнений, теперь уже с использованием контекста и блоков буферизации данных TOWS_c.

Добавьте 3 блока буферизации TOWS_c – по одному для каждой переменной моделируемой системы.

Во внутренних параметров каждого из блоков TOWS_c укажите число запоминаемых точек = 10000 и задайте ассоциируем имена переменных x_var, y_var, z_var в соответствии с сигналами, подающимися на регулярные входы TOWS_c (см. рис. 64).

Рисунок 64. Блоки буферизации, включенные блок-схему системы (1)

Теперь значения переменных ( x,y,z ) для всех временных отсчетов записываются в одноимённые переменные x_var, y_var, z_var. Эти переменные можно использовать в контексте для построения графиков посредством стандартных Scilab – функций, например plot() и param3d().

Для того, чтобы отобразить две системы координат в одном графическом окне, добавьте в контекст следующие строки:

После запуска моделирования, появится одно графическое окно: на первой координатной сетке будут зависимости ( x(t), y(t), z(t) ), а на второй – трёхмерный график аттрактора Рёсслера. как на рис. 65.