Очень часто в ряде наук встречается ситуация, когда модель рассматриваемого процесса сводится к дифференциальному уравнению. Причём, в большинстве реальных задач это уравнение довольно сложно решить, или совсем невозможно. И вот тут в полный голос звучит извечный вопрос: как быть?
Встречайте: фазовые портреты (они же фазовые диаграммы). Простым языком, фазовый портрет — это то, как величины, описывающие состояние системы (a.k.a. динамические переменные), зависят друг от друга. В случае механического движения это координата и скорость, в электричестве это заряд и ток, в известной популяционной задаче это количество хищников и жертв и т.д.
Чем хороши фазовые портреты? А тем, что их можно построить не решая динамические уравнения системы. В некоторых случаях построение фазового портрета становится совсем простой задачей. Однако, одновременно с этим, фазовые портреты дают вдумчивому наблюдателю очень много информации о поведении системы.
Начнём с простого примера — малых колебаний (так же называемых гармоническими). Малые колебания встречаются почти в каждой сфере естественных наук. Для определённости, будем рассматривать колебания металлического стержня, подвешенного за один из концов (частный случай так называемого физического маятника). Можно показать, что его колебания описываются следующим дифференциальным уравнением:
Где x — угол отклонения стержня от вертикали, точка над x означает производную по времени, а коэффициент перед синусом зависит от размера и массы стержня.
Если амплитуда (размах) колебаний достаточно мала, синус можно приближенно заменить его аргументом (вы ведь помните первый замечательный предел, нет?). В таком случае, уравнение принимает следующий вид:
Это уравнение легко решается регулярными методами, но, давайте, попробуем применить к нему метод фазовых портретов. Для этого, домножим уравнение на производную и проинтегрируем его один раз по времени:
Получилось выражение, первый член которого выглядит как кинетическая энергия. Это не случайно — на самом деле мы получили именно закон сохранения энергии. Постоянная Е в правой части (полная энергия системы на единицу массы) может принимать различные значения, которые соответствуют разным начальным состояниям системы.
Полученный нами закон сохранения превратился в уравнение кривой на плоскости (x,u):
Для разных значений Е мы получим разные кривые. Нарисуем несколько таких линий для разных значений энергии:

По горизонтальной оси отложена величина x, по вертикальной — u
Каждая из полученных линий называется фазовой траекторией. Когда меняется состояние системы, изображающая её точка движется по одной из этих траекторий, стрелки указывают направление движения изображающей точки.
По графику видно, что значения скорости и координаты меняются циклическим образом, то есть периодически повторяются. Отсюда можно сделать вывод, что описываемая рассмотренным уравнением система будет совершать колебания. Бинго! Именно так ведёт себя маятник, и если решить уравнение, решение будет иметь вид периодических функций (а именно — комбинации синуса и косинуса).
Следует однако помнить, что замена синуса его аргументом оправдана лишь для малых углов отклонения (от 10 градусов и меньше), поэтому мы не можем доверять тем траекториям, которые выходят за границы области, ограниченной жирными пунктирными линиями, то есть из четырех приведенных траекторий лишь оранжевая достоверно отображает реальность. Кроме того, поскольку x это угол, то его значения, соответствующие 180 и -180 градусам описывают одно и то же положение стержня, то есть правая и левая пунктирные линии (тонкие) на графике это на самом деле одна и та же линия.
Теперь, поскольку нам понятна суть, можно перейти к чему-то посложнее. Выше мы очень сильно упростили уравнение и при этом ограничили себя только малыми колебаниями. Математик бы сказал, что мы линеаризовали уравнение и пренебрегли нелинейными эффектами. Так давайте включим в рассмотрение нелинейность. Вернёмся к самому первому уравнению — с синусом. Если мы повторим с ним то, что проделали с линейным уравнением, мы получим следующий закон сохранения:
В зависимости от значения энергии, мы опять получаем разные кривые, которые приведены на следующем рисунке, причем выбраны те же значения энергии, что и на первой диаграмме, и те же цвета для линий.
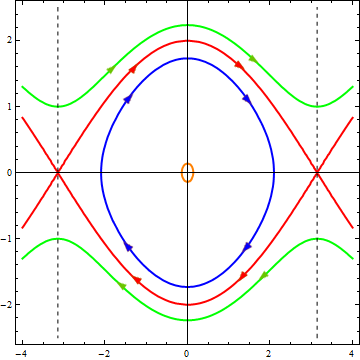
По горизонтальной оси отложена величина x, по вертикальной — u
Как видите, процессы происходящее в системе стали более разнообразными:
При малых энергиях (оранжевая и синяя траектории) существует колебательный режим, но колебания уже не являются гармоническими — фазовые траектории уже не имеют форму эллипсов.
При больших энергиях (зеленая траектория) колебаний уже нет, вместо этого мы получаем вращательное движение с переменной скоростью. И действительно, если достаточно сильно «толкнуть» стержень, он будет вращаться, замедляясь при подъёме и ускоряясь при спуске.
При определенном промежуточном значении энергии получается особый набор траекторий, которые отделяют друг от друга области соответствующие разным типам движения и поэтому называются сепаратрисами. И да, значение энергии для красной кривой было выбрано мной именно так, чтобы в нелинейном случае получилась сепаратриса. Каждая ветвь сепаратрисы это траектория, соответствующая особому типу движения. Посмотрим на диаграмму: движение начинается с очень маленькой скоростью от одного крайнего положения стержня, при приближении к положению равновесия скорость растёт, а после изображающая точка все более замедляясь уходит к крайнему положению, где и останавливается. Это соответствует тому, что мы поднимаем стержень вертикально вверх и отпускаем его, проносясь через положение равновесия он поднимается к верхней точке с другой стороны и останавливается.
А теперь давайте посмотрим насколько близки к истине наши выводы, сделанные на основе фазовых портретов. Перед вами график решения линейного уравнения:

По горизонтальной оси отложено время, по вертикальной — x
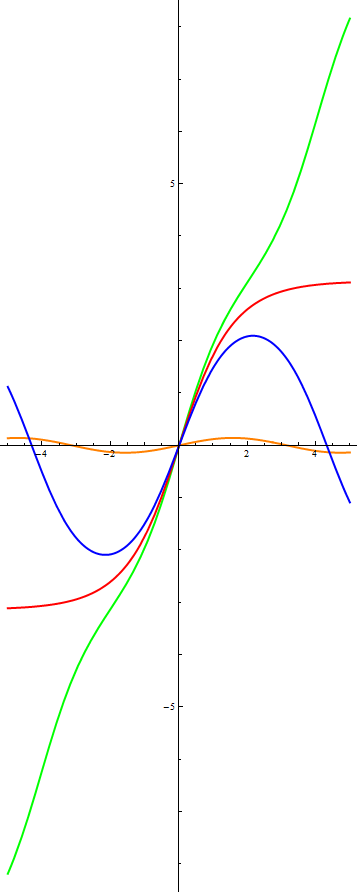
По горизонтальной оси отложено время, по вертикальной — x
Цветовая маркировка на этих графиках такая же, как и на фазовых портретах. Судить о том, насколько верные выводы были сделаны на основе фазовых портретов я предоставлю вам, дорогие читатели. Обращу ваше внимание только на один момент — колебания в линейном случае происходят синхронно — с одной и той же частотой. В нелинейном же случае, частота колебания с большей амплитудой (синяя линия) оказывается меньше, чем у колебания с малой амплитудой (оранжевая линия). Это служит еще одним подтверждением того, что нелинейные колебания не являются гармоническими.
Ну и напоследок: это всего лишь поверхностный экскурс в метод фазовых портретов, и словосочетание «на пальцах» попало в заголовок неспроста. Те же, кто решит углубиться в перипетии данного предмета, увидят, что за фазовыми портретами скрывается намного большее.
Видео:Лекция №5 Фазовые траектории автономных систем (разбор примеров)Скачать

ЛЕКЦИЯ 4
Модели, описываемые системами двух автономных дифференциальных уравнений.
Фазовая плоскость. Фазовый портрет. Метод изоклин. Главные изоклины. Устойчивость стационарного состояния. Линейные системы. Типы особых точек: узел, седло, фокус, центр. Пример: химические реакции первого порядка.
Наиболее интересные результаты по качественному моделированию свойств биологических систем получены на моделях из двух дифференциальных уравнений, которые допускают качественное исследование с помощью метода фазовой плоскости. Рассмотрим систему двух автономных обыкновенных дифференциальных уравнений общего вида
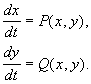
P(x,y), Q(x,y) — непрерывные функции, определенные в некоторой области G евклидовой плоскости ( x,y ‑ декартовы координаты) и имеющие в этой области непрерывные производные порядка не ниже первого.
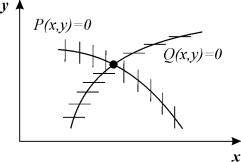
Область G может быть как неограниченной, так и ограниченной. Если переменные x, y имеют конкретный биологический смысл (концентрации веществ, численности видов) чаще всего область G представляет собой положительный квадрант правой полуплоскости:
Концентрации веществ или численности видов также могут быть ограничены сверху объемом сосуда или площадью ареала обитания. Тогда область значений переменных имеет вид:
Переменные x, y во времени изменяются в соответствии с системой уравнений (4.1), так что каждому состоянию системы соответствует пара значений переменных ( x, y) .
Изображающая точка на фазовой плоскости
 |
Обратно, каждой паре переменных ( x, y) соответствует определенное состояние системы.
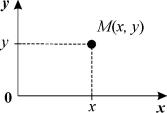
Рассмотрим плоскость с осями координат, на которых отложены значения переменных x,y. Каждая точка М этой плоскости соответствует определенному состоянию системы. Такая плоскость носит название фазовой плоскости и изображает совокупность всех состояний системы. Точка М(x,y) называется изображающей или представляющей точкой.
Пусть в начальный момент времени t=t0 координаты изображающей точки М0( x( t0) , y( t0)) . В каждый следующий момент времени t изображающая точка будет смещаться в соответствии с изменениями значений переменных x( t) , y( t) . Совокупность точек М( x( t) , y(t)) на фазовой плоскости, положение которых соответствует состояниям системы в процессе изменения во времени переменных x(t), y(t) согласно уравнениям (4.1), называется фазовой траекторией.
Совокупность фазовых траекторий при различных начальных значениях переменных дает легко обозримый «портрет» системы. Построение фазового портрета позволяет сделать выводы о характере изменений переменных x, y без знания аналитических решений исходной системы уравнений (4.1).
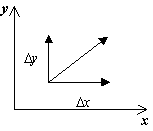
Для изображения фазового портрета необходимо построить векторное поле направлений траекторий системы в каждой точке фазовой плоскости. Задавая приращение D t>0, получим соответствующие приращения D x и D y из выражений:
Направление вектора dy/dx в точке ( x, y) зависит от знака функций P(x, y), Q(x, y) и может быть задано таблицей:
Задача построения векторного поля упрощается, если получить выражение для фазовых траекторий в аналитическом виде. Для этого разделим второе из уравнений системы (4.1) на первое:
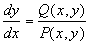
Решение этого уравнения y = y( x, c) , или в неявном виде F( x,y) =c, где с – постоянная интегрирования, дает семейство интегральных кривых уравнения (4.2) ‑ фазовых траекторий системы (4.1) на плоскости x, y.
Для построения фазового портрета пользуются методом изоклин – на фазовой плоскости наносят линии, которые пересекают интегральные кривые под одним определенным углом. Уравнение изоклин легко получить из (4.2). Положим
где А – определенная постоянная величина. Значение А представляет собой тангенс угла наклона касательной к фазовой траектории и может принимать значения от – ¥ до + ¥ . Подставляя вместо dy/dx в (4.2) величину А получим уравнение изоклин:
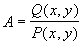
Уравнение (4.3) определяет в каждой точке плоскости единственную касательную к соответствующей интегральной кривой за исключением точки, где P (x,y) = 0, Q ( x,y) = 0, в которой направление касательной становится неопределенным, так как при этом становится неопределенным значение производной:
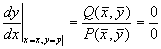
Эта точка является точкой пересечения всех изоклин – особой точкой. В ней одновременно обращаются в нуль производные по времени переменных x и y.
Таким образом, в особой точке скорости изменения переменных равны нулю. Следовательно, особая точка дифференциальных уравнений фазовых траекторий (4.2) соответствует стационарному состоянию системы (4.1), а ее координаты – суть стационарные значения переменных x, y.
Особый интерес представляют главные изоклины:
dy/dx=0, P ( x,y) =0 – изоклина горизонтальных касательных и
dy/dx= ¥ , Q ( x,y) =0 – изоклина вертикальных касательных.
Построив главные изоклины и найдя точку их пересечения (x,y), координаты которой удовлетворяют условиям:
мы найдем тем самым точку пересечения всех изоклин фазовой плоскости, в которой направление касательных к фазовым траекториям неопределенно. Это – особая точка, которая соответствует стационарному состоянию системы (рис. 4.2).
Система (4.1) обладает столькими стационарными состояниями, сколько точек пересечения главных изоклин имеется на фазовой плоскости.
Каждая фазовая траектория соответствует совокупности движений динамической системы, проходящих через одни и те же состояния и отличающихся друг от друга только началом отсчета времени.
Рис. 4.2. Пересечение главных изоклин на фазовой плоскости.
 |
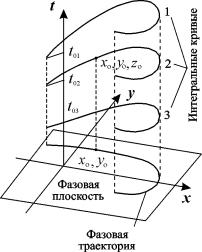
Таким образом, фазовые траектории системы – это проекции интегральных кривых в пространстве всех трех измерений x, y, t на плоскость x, y (рис.4.3).
Рис. 4.3. Траектории системы в пространстве ( x, y, t).
 |
Если условия теоремы Коши выполнены, то через каждую точку пространства x, y, t проходит единственная интегральная кривая. То же справедливо, благодаря автономности, для фазовых траекторий: через каждую точку фазовой плоскости проходит единственная фазовая траектория.
Устойчивость стационарного состояния
Пусть система находится в состоянии равновесия.
Тогда изображающая точка находится в одной из особых точек системы, в которых по определению:
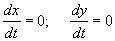
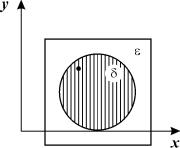
Устойчива или нет особая точка, определяется тем, уйдет или нет изображающая точка при малом отклонении от стационарного состояния. Применительно к системе из двух уравнений определение устойчивости на языке e , d выглядит следующим образом.
Состояние равновесия устойчиво, если для любой заданной области отклонений от состояния равновесия ( e ) можно указать область d ( e ) , окружающую состояние равновесия и обладающую тем свойством, что ни одна траектория, которая начинается внутри области d , никогда не достигнет границы e . (рис. 4.4)
Иллюстрация к определению устойчивости области e и d на плоскости ( x,y)
 |
Для большого класса систем – грубых систем – характер поведения которых не меняется при малом изменении вида уравнений, информацию о типе поведения в окрестности стационарного состояния можно получить, исследуя не исходную, а упрощенную линеаризованную систему.
Рассмотрим систему двух линейных уравнений:
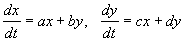
Здесь a, b, c, d — константы, x, y ‑ декартовы координаты на фазовой плоскости.
Общее решение будем искать в виде:
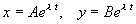
Подставим эти выражения в (4.4) и сократим на e l t :

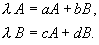
Алгебраическая система уравнений (4.6) с неизвестными A, B имеет ненулевое решение лишь в том случае, если ее определитель, составленный из коэффициентов при неизвестных, равен нулю:
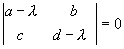
Раскрывая этот определитель, получим характеристическое уравнение системы:
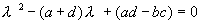
Решение этого уравнения дает значения показателя l 1,2 , при которых возможны ненулевые для A и B решения уравнения (4.6). Эти значения суть
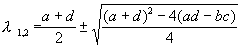
Если подкоренное выражение отрицательно, то l 1,2 комплексно сопряженные числа. Предположим, что оба корня уравнения (4.7) имеют отличные от нуля действительные части и что нет кратных корней. Тогда общее решение системы (4.4) можно представить в виде линейной комбинации экспонент с показателями l 1 , l 2 :
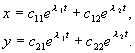
Для анализа характера возможных траекторий системы на фазовой плоскости используем линейное однородное преобразование координат, которое позволит привести систему к каноническому виду:
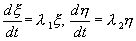
допускающее более удобное представление на фазовой плоскости по сравнению с исходной системой (4.4). Введем новые координаты ξ , η по формулам:

Из курса линейной алгебры известно, что в случае неравенства нулю действительных частей l 1 , l 2 исходную систему (4.4) при помощи преобразований (4.11) всегда можно преобразовать к каноническому виду (4.10) и изучать ее поведение на фазовой плоскости ξ , η . Рассмотрим различные случаи, которые могут здесь представиться.
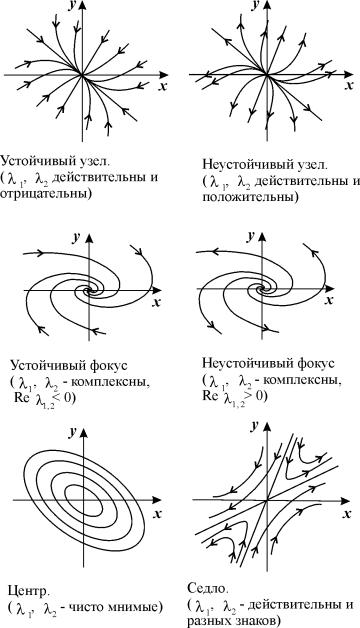
Корни λ 1 , λ 2 – действительны и одного знака
В этом случае коэффициенты преобразования действительны, мы переходим от действительной плоскости x,y к действительной плоскости ξ, η. Разделив второе из уравнений (4.10) на первое, получим :
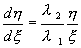
Интегрируя это уравнение, находим :
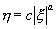
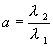
Условимся понимать под λ 2 корень характеристического уравнения с большим модулем, что не нарушает общности нашего рассуждения. Тогда, поскольку в рассматриваемом случае корни λ 1 , λ 2 – действительны и одного знака, a >1 , и мы имеем дело с интегральными кривыми параболического типа.
Все интегральные кривые (кроме оси η, которой соответствует 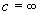
Выясним теперь направление движений изображающей точки вдоль фазовых траекторий. Если λ 1 , λ 2 – отрицательны, то, как видно из уравнений (4.10), |ξ|, |η| убывают с течением времени. Изображающая точка приближается к началу координат, никогда, однако, не достигая его. В противном случае это противоречило бы теореме Коши, которая утверждает, что через каждую точку фазовой плоскости проходит лишь одна фазовая траектория.
Такая особая точка, через которую проходят интегральные кривые, подобно тому, как семейство парабол 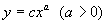
Рис. 4.5. Особая точка типа узел на плоскости канонических координат ξ, η
Состояние равновесия типа узел при λ 1 , λ 2 0 устойчиво по Ляпунову, так как изображающая точка по всем интегральным кривым движется по направлению к началу координат. Это устойчивый узел. Если же λ 1 , λ 2 > 0, то |ξ|, |η| возрастают с течением времени и изображающая точка удаляется от начала координат. В этом случае особая точка – неустойчивый узел .
На фазовой плоскости x, y общий качественный характер поведения интегральных кривых сохранится, но касательные к интегральным кривым не будут совпадать с осями координат. Угол наклона этих касательных будет определяться соотношением коэффициентов α , β , γ , δ в уравнениях (4.11).
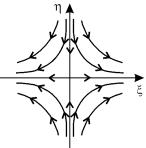
Корни λ 1 , λ 2 – действительны и разных знаков.
Преобразование от координат x,y к координатам ξ, η опять действительное. Уравнения для канонических переменных снова имеют вид (4.10), но теперь знаки λ 1 , λ 2 различны. Уравнение фазовых траекторий имеет вид :
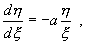
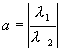
Интегрируя (4.14), находим
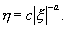
Это уравнение определяет семейство кривых гиперболического типа, где обе оси координат – асимптоты (при a=1 мы имели бы семейство равнобочных гипербол) . Оси координат и в этом случае являются интегральными кривыми – это будут единственные интегральные кривые, проходящие через начало координат. Каждая из них состоит из трех фазовых траекторий : из двух движений к состоянию равновесия (или от состояния равновесия) и из состояния равновесия. Все остальные интегральные кривые – суть гиперболы, не проходящие через начало координат (рис. 4.6) Такая особая точка носит название «седло ». Линии уровня вблизи горной седловины ведут себя подобно фазовым траекториям в окрестности седла.
Рис. 4.6. Особая точка типа седло на плоскости канонических координат ξ , η
Рассмотрим характер движения изображающей точки по фазовым траекториям вблизи состояния равновесия. Пусть, например, λ 1 >0 , λ 2 . Тогда изображающая точка, помещенная на оси ξ, будет удаляться от начала координат, а помещенная на оси η – будет неограниченно приближаться к началу координат , не достигая его за конечное время . Где бы ни находилась изображающая точка в начальный момент (за исключением особой точки и точек на асимптоте η =0), она в конечном счете будет удаляться от состояния равновесия, даже если в начале она движется по одной из интегральных кривых по направлению к особой точке .
Очевидно, что особая точка типа седла всегда неустойчива . Только при специально выбранных начальных условиях на асимптоте η =0 система будет приближаться к состоянию равновесия. Однако это не противоречит утверждению о неустойчивости системы. Если считать , что все начальные состояния системы на фазовой плоскости равновероятны, то вероятность такого начального состояния, которое соответствует движению по направлению к особой точке, равна нулю. Поэтому всякое реальное движение будет удалять систему от состояния равновесия. Переходя обратно к координатам x,y, мы получим ту же качественную картину характера движения траекторий вокруг начала координат.
Пограничным между рассмотренными случаями узла и седла является случай, когда один из характеристических показателей, например λ 1 , обращается в нуль, что имеет место, когда определитель системы – выражение ad-bc=0 (см. формулу 4.8 ). В этом случае коэффициенты правых частей уравнений (4.4) пропорциональны друг другу :
и система имеет своими состояниями равновесия все точки прямой :
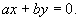
Остальные интегральные кривые представляют собой семейство параллельных прямых с угловым коэффициентом 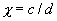
Рис. 4.7. Фазовый портрет системы, один из характеристических корней которой равен нулю, а второй отрицателен.
В этом случае при действительных x и y мы будем иметь комплексные сопряженные ξ , η ( 4.10) . Однако , вводя еще одно промежуточное преобразование, можно и в этом случае свести рассмотрение к действительному линейному однородному преобразованию. Положим :
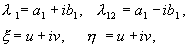
где a,b, и u,v – действительные величины. Можно показать, что преобразование от x,y к u,v является при наших предположениях действительным, линейным, однородным с детерминантом, отличным от нуля. В силу уравнений (4.10, 4.16) имеем :
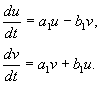
Разделив второе из уравнений на первое , получим :
которое легче интегрируется , если перейти к полярной системе координат ( r, φ ) . После подстановки 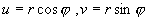
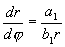
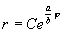
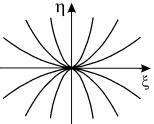
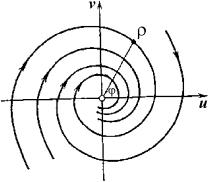
Таким образом, на фазовой плоскости u, v мы имеем дело с семейством логарифмических спиралей, каждая из которых имеет асимптотическую точку в начале координат. Особая точка, которая является асимптотической точкой всех интегральных кривых, имеющих вид спиралей , вложенных друг в друга, называется фокусом ( рис.4.8 ) .
Рис. 4.8. Фазовый портрет системы в окрестности особой точки типа фокус на плоскости координат u, v .
Рассмотрим характер движения изображающей точки по фазовым траекториям. Умножая первое из уравнений (4.17) на u , а второе на v и складывая , получаем :
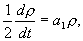
Пусть a 1 0 ( a 1 = Re λ ) . Изображающая точка тогда непрерывно приближается к началу координат, не достигая его в конечное время. Это означает, что фазовые траектории представляют собой скручивающиеся спирали и соответствуют затухающим колебаниям переменных. Это – устойчивый фокус .
В случае устойчивого фокуса, как и в случае устойчивого узла, выполнено не только условие Ляпунова, но и более жесткое требование. Именно, при любых начальных отклонениях система по прошествии времени вернется как угодно близко к положению равновесия. Такая устойчивость, при которой начальные отклонения не только не нарастают, но затухают, стремясь к нулю, называют абсолютной устойчивостью .
Если в формуле (4.18) a1 >0 , то изображающая точка удаляется от начала координат, и мы имеем дело с неустойчивым фокусом . При переходе от плоскости u,v к фазовой плоскости x , y спирали также останутся спиралями, однако будут деформированы.
Рассмотрим теперь случай, когда a 1 =0 . Фазовыми траекториями на плоскости u, v будут окружности 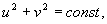
Таким образом, при a1 =0 через особую точку x= 0 , y=0 не проходит ни одна интегральная кривая. Такая изолированная особая точка, вблизи которой интегральные кривые представляют собой замкнутые кривые, в частности, эллипсы, вложенные друг в друга и охватывающие особую точку, называется центром.
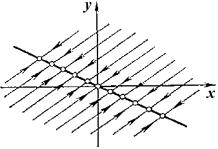
Таким образом, возможны шесть типов состояния равновесия в зависимости от характера корней характеристического уравнения (4.7). Вид фазовых траекторий на плоскости x, y для этих шести случаев изображен на рис. 4.9.
Рис. 4.9. Типы фазовых портретов в окрестности стационарного состояния для системы линейных уравнений (4.4).
Пять типов состояния равновесия грубые, их характер не изменяется при достаточно малых изменениях правых частей уравнений (4.4). При этом малыми должны быть изменения не только правых частей, но и их производных первого порядка. Шестое состояние равновесия – центр – негрубое. При малых изменениях параметров правой части уравнений он переходит в устойчивый или неустойчивый фокус.
Видео:Дифференциальные уравнения 6. Фазовые траектории. Особые точки автономных системСкачать

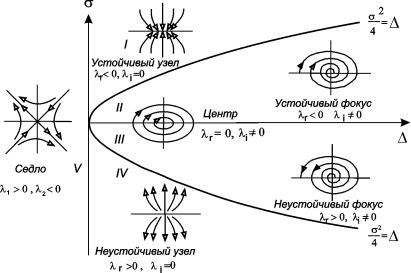
Бифуркационная диаграмма
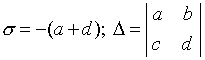
Тогда характеристическое уравнение запишется в виде:
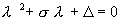
Рассмотрим плоскость с прямоугольными декартовыми координатами s , D и отметим на ней области, соответствующие тому или иному типу состояния равновесия, который определяется характером корней характеристического уравнения
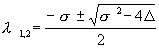
Условием устойчивости состояния равновесия будет наличие отрицательной действительной части у l 1 и l 2 . Необходимое и достаточное условие этого – выполнение неравенств s > 0, D > 0 . На диаграмме (4.15) этому условию соответствуют точки, расположенные в первой четверти плоскости параметров. Особая точка будет фокусом, если l 1 и l 2 комплексны. Этому условию соответствуют те точки плоскости, для которых 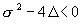
Рис. 4.10. Бифуркационная диаграмма
для системы линейных уравнений 4.4
Если коэффициенты линейной системы a, b, c, d зависят от некоторого параметра, то при изменении этого параметра будут меняться и величины s , D . При переходе через границы характер фазового портрета качественно меняется. Поэтому такие границы называются бифуркационными – по разные стороны от границы система имеет два топологически различных фазовых портрета и, соответственно два разных типа поведения.
На диаграмме видно, как могут проходить такие изменения. Если исключить особые случаи – начало координат, – то легко видеть, что седло может переходить в узел, устойчивый или неустойчивый при пересечении оси ординат. Устойчивый узел может перейти либо в седло, либо в устойчивый фокус, и т.д. Отметим, что переходы устойчивый узел – устойчивый фокус и неустойчивый узел – неустойчивый фокус не являются бифуркационными, так как топология фазового пространства при этом не меняется. Более подробно мы поговорим о топологии фазового пространства и бифуркационных переходах в лекции 6.
При бифуркационных переходах меняется характер устойчивости особой точки. Например, устойчивый фокус через центр может переходить в неустойчивый фокус. Эта бифуркация называется бифуркацией Андронова-Хопфа по именам исследовавших ее ученых. При этой бифуркации в нелинейных системах происходит рождение предельного цикла, и система становится автоколебательной (см. лекцию 8).
Пример. Система линейных химических реакций
Вещество Х притекает извне с постоянной скоростью, превращается в вещество Y и со скоростью, пропорциональной концентрации вещества Y, выводится из сферы реакции. Все реакции имеют первый порядок, за исключением притока вещества извне, имеющего нулевой порядок. Схема реакций имеет вид:
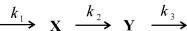
и описывается системой уравнений:
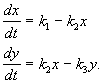
Стационарные концентрации получим, приравняв правые части нулю:
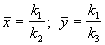
Рассмотрим фазовый портрет системы. Разделим второе уравнение системы (4.16) на первое. Получим:
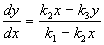
Уравнение (4.17) определяет поведение переменных на фазовой плоскости. Построим фазовый портрет этой системы. Сначала нарисуем главные изоклины на фазовой плоскости. Уравнение изоклины вертикальных касательных:
Уравнение изоклины горизонтальных касательных:
Особая точка (стационарное состояние) лежит на пересечении главных изоклин.
Теперь определим, под каким углом пересекаются координатные оси интегральными кривыми.
Если x=0, то 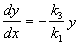
Таким образом, тангенс угла наклона касательной к интегральным кривым y=y(x), пересекающим ось ординат x=0, отрицателен в верхней полуплоскости (вспомним, что переменные x, y имеют значения концентраций, и поэтому нас интересует только правый верхний квадрант фазовой плоскости). При этом величина тангенса угла наклона касательной увеличивается с удалением от начала координат.
Рассмотрим ось y=0 . В месте пересечения этой оси интегральными кривыми они описываются уравнением
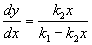
При 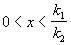
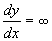
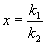
Затем при дальнейшем увеличении тангенс угла наклона уменьшается по абсолютной величине, оставаясь отрицательным и стремится к -1 при x ® ¥ . Зная направление касательных к интегральным кривым на главных изоклинах и на осях координат, легко построить всю картину фазовых траекторий.
Рис. 4.12. Фазовый портрет системы линейных химических реакций (4.15)
Видео:Асташова И. В. - Дифференциальные уравнения. Часть 2 - Фазовый портретСкачать

Фазовые траектории систем дифференциальных уравнений
Система обыкновенных дифференциальных уравнений называется автономной, если независимая переменная не входит явно в систему.
В теории автономных систем принято обозначать независимую переменную буквой t, а искомое решение — 
Ограничимся случаем n = 2 и в дальнейшем рассматриваем автономные системы второго порядка: 
Будем полагать, что правые части системы f1(x1, x2 ) , f2(x1, x2) непрерывно дифференцируемы в области 
Пусть x1=j1(t), x2= j2(t) — решение автономной системы второго порядка. Тогда уравнения 
задают в параметрической форме кривую на плоскости. Эта кривая называется фазовой кривой или фазовой траекторией системы. Плоскость, на которой расположены фазовые траектории называется фазовой плоскостью автономной системы. Для n >2 фазовые траектории располагаются в фазовом пространстве.
Если на рисунке изображено несколько фазовых кривых системы, характеризующих качественное поведение решений системы (кривые с одинаковыми асимптотами, предельными точками и пр.), то такое изображение называется фазовым портретом системы.
Интегральные кривые рассматриваемой системы изображаются в трехмерном пространстве переменных (t, x1, x2) и, если x1= f 1(t), x2= f 2(t) — решение системы, то интегральная кривая задается в параметрической форме уравнениями 
а фазовая траектория — не что иное, как проекция интегральной кривой на фазовую плоскость (плоскость (x1, x2).
ПРИМЕР 1. Фазовые кривые автономной системы.
Для фазовых кривых (фазовых траекторий) автономной системы с непрерывно дифференцируемой правой частью 

справедливы следующие утверждения:
- Если существует такая точка
, что
, то
, является решением автономной системы, т.е. соответствующая фазовая траектория — точка.
- Если точка (x1(t), x2(t)) принадлежит некоторой фазовой кривой, то при любой постоянной С точка (x1(t+С), x2(t+С)) принадлежит той же фазовой кривой.
- Две фазовые кривые либо не имеют общих точек, либо совпадают.
- Фазовая траектория, отличная от точки, есть гладкая кривая (в каждой ее точке есть ненулевой касательный вектор).
- Всякая фазовая кривая принадлежит к одному из трех типов— гладкая кривая без самопересечений, замкнутая гладкая кривая (цикл), точка.
- Если фазовая кривая, отвечающая решению
, есть гладкая замкнутая кривая, то это решение — периодическая функция.
ПРИМЕР 2. Типы фазовых кривых.
Точка 

ПРИМЕР 3. Точки покоя автономной системы.
Если в каждой точке области 



в векторной форме: 
где 

Автономная система 
полностью определяется заданием векторного поля 
Действительно, в каждой точке 
гладкой фазовой кривой

существует касательный вектор
(x'(t0 ), y'(t0 ))
равный (в силу системы) вектору 
иными словами, векторное поле 
автономной системы задает в каждой точке направление касательной к фазовой кривой системы, проходящей через эту точку.
Точки векторного поля, в которых вектор 
ПРИМЕР 4. Векторное поле автономной системы.
Исправляем ошибки: Нашли опечатку? Выделите ее мышкой и нажмите Ctrl+Enter
📺 Видео
Волков В. Т. - Дифференциальные уравнения - Фазовая плоскость. Фазовые траектории и их видыСкачать

Дополнительные главы ИДУ: Построение фазовых портретов | Занятие 3Скачать

Решение системы дифференциальных уравнений методом ЭйлераСкачать

ТАУ. Matlab/SIMULINK Фазовые портреты систем нелинейных диф. уравненийСкачать

4. Исследование фазовых траекторий.Скачать

Дифференциальные уравнения 3. Автономные системыСкачать

Асташова И. В. - Дифференциальные уравнения. Часть 2 - Лекция 11Скачать

Дифференциальные уравнения 20. Исследование поведения фазовых траекторийСкачать

18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать

Видеоурок "Системы дифференциальных уравнений"Скачать

Устойчивость 1 ОпределениеСкачать

Линейная алгебра. Алексей Савватеев и Александр Тонис. Лекция 3.5. Линеаризация систем диф.уровСкачать


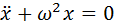




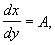
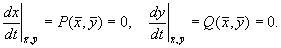
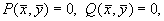
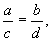
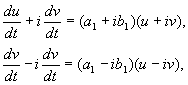
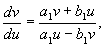
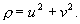
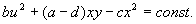
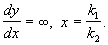
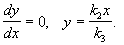
 , является решением автономной системы, т.е. соответствующая фазовая траектория — точка.
, является решением автономной системы, т.е. соответствующая фазовая траектория — точка. , есть гладкая замкнутая кривая, то это решение — периодическая функция.
, есть гладкая замкнутая кривая, то это решение — периодическая функция.