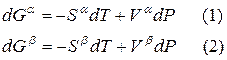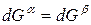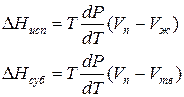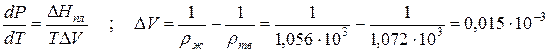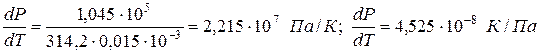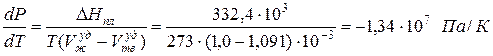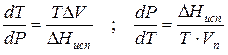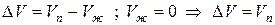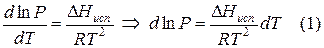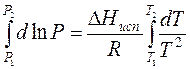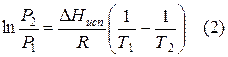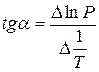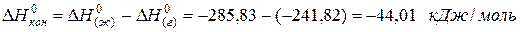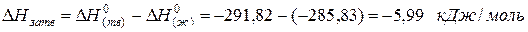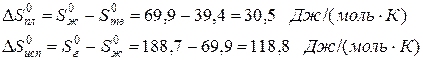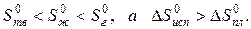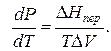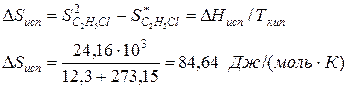Фазовые равновесия в однокомпонентных системах уравнение клапейрона клаузиуса (2 видео)

Однокомпонентные системы. Фазовые равновесия однокомпонентных систем, уравнение Клапейрона

В однокомпонентных системах могут существовать следующие фазовые равновесия (фазовые равновесия первого рода):

Кристаллическая фаза аморфная фаза.

Процесс в прямом направлении называют плавлением, а в обратном — кристаллизацией:

Аморфная фаза газообразная фаза.

Процесс в прямом направлении называют испарением (кипением), а в обратном — конденсацией:

Кристаллическая фаза газообразная фаза.

Процесс, протекающий в прямом направлении, называют возгонкой (сублимацией), а в обратном — конденсацией (десублимацией).

Для вывода уравнения, связывающего давление Р и температуру Т равновесных фаз, рассмотрим термодинамику фазового равновесия:

где а и (3 — равновесные фазы. При равновесии химические потенциалы фаз равны ра = р(3. Изменим давление и температуру системы на бесконечно малые величины dP и dT так, чтобы равновесие в системе не нарушилось. Если после изменения параметров равновесие сохранилось, то новые значения химического потенциала равновесных фаз вновь равны друг другу: р(( = рр.

Если равны значения р и р’ равновесных фаз, то равны и их изменения — dp. Для чистых веществ р — G_m, тогда dp — dG_m — -SdT + VdP

Приравняв друг к другу уравнения (3.11) и (3.12) и перегруппировав слагаемые, получаем:

Индекс «ФП» означает, что изменение S или V относится к фазовому переходу. Для фазового перехода (Г и Р = const) изменение энтропии равно:

Окончательно имеем уравнение

Уравнения (3.13) и (3.14) связывают температуру и давление равновесных фаз, они носят имя Э. П. Б. Клапейрона (уравнение Клапейрона).

Содержание

Диаграммы фазового равновесия однокомпонентных систем
Фазовые равновесия. Правило фаз Гиббса. Классификация систем. Фазовые равновесия в однокомпонентных системах. Уравнение Клапейрона-Клаузиуса. Диаграммы состояния однокомпонентных систем.
Клапейрона–Клаузиуса
💥 Видео

Видео:Физическая химия # 2. Вывод уравнения Клаузиуса-КлапейронаСкачать

Диаграммы фазового равновесия однокомпонентных систем

Теории, количественно описывающей состояние конденсированных фаз, в настоящее время не существует. По этой причине связь давления и температуры в фазах однокомпонентной системы при фазовых равновесиях устанавливают экспериментально и полученные опытные данные располагают в координатах Р = /(Т). График такой зависимости для всех фазовых равновесий индивидуального вещества называют диаграммой фазового равновесия однокомпонентной системы. На рис. 3.1 в качестве примера приведена такая диаграмма.

Здравый смысл (наш повседневный опыт) подсказывает, что при достаточно высоких давлениях и низких температурах стабильной фазой веществ является кристаллическое состояние. Кристаллические вещества чаще всего находятся в твердом агрегатном состоянии (кроме жидких кристаллов), поэтому на диаграммах вместо термина «кристаллическая фаза» обычно указывают: «твердая фаза».

При достаточно высоких температурах и низких давлениях стабильной фазой вещества является газообразная фаза: на диаграммах указывают: «газ». В промежуточных значениях Р и Т между рассмотренными фазами вещества находится в аморфном состоянии. Аморфные вещества обычно — жидкости (исключение составляют полимеры в стеклообразном или высокоэластическом состояниях — они твердые, но аморфные), поэтому на диаграммах пишут «жидкость». В дальнейшем сокращенно будем обозначать фазовые равновесия так: тв«жо о г и т. д.

Рис. 3.1. Диаграмма фазового равновесия однокомпонентной системы:

О — тройная точка; кр — критическая точка, Т_нтк — температура кипения жидкости при нормальном давлении (1 атм)

Существуют давления и температуры, при которых в равновесии одновременно находятся две фазы, эти значения Р и Т определяет уравнение Клапейрона (3.14). Проанализируем фазовые равновесия однокомпонентных систем, используя уравнение (3.14).

Равновесие твердое тело •?=> жидкость (кристаллы аморфная фаза). Для плавления (процесс в прямом направлении) уравнение Клапейрона следует записать так:

Здесь Д_ПЛУ = У_ж — У_тв — изменение объема системы при плавлении 1 моля твердого вещества (разность молярных объемов вещества в жидком и твердом состояниях). Величина Д_ПЛУ мала (ее порядок —

10 -5 —10- 6 м 3 /моль), поэтому производная — велика, а это означает,

что тангенс угла наклона касательных к кривой фазового равновесия тв ж в каждой ее точке очень велик (tga —» °°), а следовательно, и сама кривая практически вертикально направлена вверх. Это видно из рис.3.1 (линия OD). Для всех веществ, кроме воды (алмазоподобных структур), ДпдУ = У_ж — V_TB > О, Д_ПЛН > 0 (для плавления энергию следует

подводить к телу), Т > 0 (в кельвинах), тогда — > 0 и наклон линии

фазового равновесия положительный.

Одним из исключений является вода, для нее ДплУл = У_ж — V_TB У_ж), в которую она налита. Лед плавает по поверхности воды (его плотность меньше), благодаря этому факту на Земле стало возможным зарождение и существование жизни: водоемы не промерзают до дна. Следовательно, — ж отрицательный (см. рис. 3.1).

Равновесие жидкость газ (аморфная фаза газообразная фаза). Для процесса испарения (в прямом направлении) уравнение Клапейрона следует записать так:

Здесь Д_ИСПУ = V_r -У_ж — изменение объема системы при испарении 1 моля жидкости (разность молярных объемов вещества в газообразном и жидком состояниях). Для испарения Д_ИСПК велико, следовательно, dP _

производная — мала. Это означает, что наклон касательных к кривой dT

в каждой ее точке, да и наклон самой кривой фазового равновесия ж г мал (линия ОБ на рис. 3.1). Кривая ОБ монотонно возрастает с повышением температуры и заканчивается в так называемой критической точке. Критической точке соответствуют критическая температура Т_кр и критическое давление Р_кр. При Т_кр свойства равновесных пара и жидкости одинаковы (например, плотность пара равна плотности жидкости), при дальнейшем повышении температуры жидкость существовать уже не может (система будет находится в виде так называемого сверхкритического флюида).

Равновесие между жидкостью и паром является динамическим: между ними непрерывно происходит обмен молекулами, причем в единицу времени через единицу поверхности раздела фаз вылетает в пар столько же частиц, сколько их возвращается обратно. Такой пар, находящийся в равновесии с жидкостью (или твердым телом), называют насыщенным. Давление насыщенного пара вещества зависит от его природы и температуры и не зависит от давления других газообразных примесей, если они мало растворимы в данной жидкости (или в данном твердом теле). Поэтому, например, давление насыщенного пара вещества практически не зависит от внешнего давления воздуха.

Проинтегрируем уравнение (3.16) применительно к равновесию «жидкость — газ». В этом случае У_г» У_ж. Действительно, при нормальных условиях объем 1 моля жидкой воды Уж = 18 см 3 = 1,8* 10 -5 м 3 , объем одного моля водяного пара Уг = 22,4 л = 2,4-10 -2 м 3 , следовательно, вместо ДиспУ в формулу (3.16) можно подставлять Уг = У:

Предполагаем далее, что пар по своим свойствам близок к идеальному газу. Подставив в уравнение (3.17) выражение для У из уравнения Клапейрона — Менделеева (1.1) в форме

получаем (для п = 1 моль):

Уравнение (3.18) выражает зависимость давления насыщенного пара от температуры. При кипении жидкости давление насыщенного пара равно внешнему давлению, поэтому это же уравнение передает и зависимость температуры кипения жидкости от внешнего давления.

Из рис. 3.1 следует, что с понижением внешнего давления температура кипения жидкостей снижается. Этим объясняется тот факт, что высоко в горах для приготовления вареного мяса или яиц требуется существенно больше времени, чем на уровне моря (кипение воды происходит при температуре ниже 100°С). Вот почему в рационе горских народов преобладает жареное или печеное мясо, но не вареное. И наоборот, с повышением внешнего давления температура кипения жидкостей возрастает. На этом явлении основана работа скороварки: в ней приготовление пищи происходит при повышенном давлении, когда температура кипения воды превышает 100°С.

Для интегрирования уравнения (3.18) необходимо знание зависимости Д_ИСПН =/(Г). Известно, что теплота испарения с повышением температуры уменьшается вплоть до нуля при критической температуре. Однако при температурах, далеких от критической, в достаточно узком интервале температур, можно считать Д_ИСПН постоянной. Интегрируя (3.18) в предположении о постоянстве Д_ИСПН, получаем:

Уравнения вида (3.19), (3.20) называют уравнением Клаузиуса — Клапейрона.

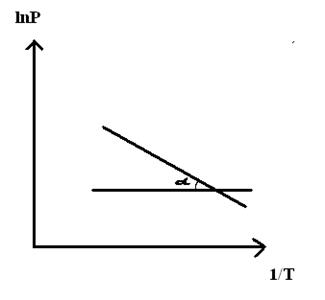
Согласно уравнению (3.19) опытные точки по зависимости давления насыщенного пара от температуры или (что одно и то же) — зависимости температуры кипения от внешнего давления в координатах 1пР = Д1/Т) должны группироваться вдоль прямой с тангенсом угла наклона, равным В = tg а = Д_ИСПН/Я (см. рис. 3.2). Константа А при этом равна отрезку, отсекаемому прямой на оси ординат.

Уравнение (3.19) служит теоретической базой для экспериментального определения теплоты испарения жидкостей (как увидим далее — и теплоты сублимации тоже). С этой целью получают экспериментальную зависимость температуры кипения от внешнего давления (откачивая в системе воздух). Полученные данные располагают в координатах 1пР от 1/Т, через опытные точки проводят прямую, вычисляют тангенс угла ее наклона и далее — Д_ИСПН.

При подобном определении теплоты испарения следует иметь в виду, что константы А и В, как и Д_ИСПН, постоянны лишь в достаточно узком интервале температур.

Можно вычислить Д_ИСПН, зная лишь два значения Р при двух значениях Т. Действительно, интегрируя уравнение (3.18) от Ру при Т_г до Р₂ при Т₂ при условии ДиспН = const, получаем:

Значение Д_ИС11Н в уравнении (3.22) зависит от величины интервала температур и оно тем ближе к истинному, чем уже этот интервал. Однако для такого вычисления Д_ИСПН требуется весьма точное измерение температуры кипения и давления пара, так как определение теплоты испарения проводят лишь по двум точкам.

Рис. 3.2. Зависимость давления насыщенного пара от температуры в линейных координатах уравнения Клаузиуса — Клапейрона

Равновесие (твердое тело) газ (кристаллическая фаза газ).

Для сублимации (процесса в прямом направлении) уравнение Клапейрона записывается так:

Здесь AcyfoV = V_r — V_TB — разность молярных объемов вещества в газообразном и твердом состояниях. Для испарения Д_ИСПК велико, а произ- dP

водная — мала, т.е. наклон касательных к кривой в каждой ее точке,

да и наклон самой кривой фазового равновесия кр г мал (линия ОС на рис. 3.1). Однако линия ОС идет несколько круче линии ОБ. Дело в том, что всегда Д_сублН > Д_ИСПН, так как теплота возгонки для чистых веществ равна сумме теплоты испарения и теплоты плавления:

Рис. 3.3. Графическая иллюстрация связи между теплотами фазовых

Это следует из применения закона Гесса к треугольнику энтальпий фазовых переходов (рис. 3.3).

Мольным объемом кристаллов по сравнению с мольным объемом газа можно пренебречь, как и при рассмотрении равновесия ж«г:

Сделав предположения, аналогичные приведенным выше, приходим к уравнению:

Оно отличается от (3.19) лишь тем, что в него вместо молярной теплоты испарения входит молярная теплота сублимации (возгонки) АсублЯ. Следовательно, и интегрирование его приведет к уравнениям, аналогичным уравнениям Клаузиуса — Клапейрона (3.19), (3.20):

Получив опытную зависимость от температуры давления насыщенного пара над твердой фазой, с помощью уравнений (2.95) и (2.96) графическим методом можно определить теплоты сублимации чистых веществ так, как это было описано выше для равновесия ж г (рис. 3.4).

Равновесие твердая фаза жидкость газ. При определенном значении Р и Т (одна точка на диаграмме) твердая, жидкая и газовая фазы могут существовать в равновесии. Геометрически эта точка находится на пересечении всех трех линий фазового равновесия (ОБ, ОС и OD). Эту точку называют тройной точкой. В таком состоянии системы все три химических потенциала фаз равны друг другу. Важно заметить, что на положение тройной точки чистого вещества мы влиять не можем. Например, в случае воды она существует при температуре 273, 1600 К и давлении 609 Па. Ни при какой другой комбинации Р и Т три фазы воды не могут сосуществовать. Это свойство позволяет использовать тройную точку при построении температурной шкалы (градусы Цельсия).

Рис. 3.4. Применение правила фаз Гиббса к диаграмме фазового равновесия однокомпонентной системе

Применим правило фаз Гиббса к диаграмме фазового равновесия однокомпонентной системы:

Вычислим число степеней свободы /в различных точках диаграммы (рис. 3.3). Система однокомпонентная, следовательно, всегда К = 1.

Во всех точках 1 Ф = 1 и, следовательно, / = 2. Это означает, что, не изменяя числа фаз (в этих точках она одна), произвольно (независимо друг от друга) можно изменять два параметра — Р и Т.

В точках 2 число равновесных фаз равно двум, т.е./ = 1. Следовательно, произвольно можно изменять только один параметр: либо Р, либо Т — изменение второго должно подстраиваться под изменение первого так, чтобы точка оставалась на кривой (число фаз оставалось равным двум).

В тройной точке О Ф = 3 (все три фазы находятся в равновесии) и / = 0: следовательно, система инвариантна, т.е. тройная точка существует при строго определенных значениях Р и Т. Если даже незначительно изменится один из параметров, то обязательно исчезнет хотя бы одна из фаз. Так, при понижении температуры закристаллизуется жидкость, а при повышении давления сконденсируется газ: в любом случае система станет двухфазной.

На рис. 3.5 и 3.6. приведены диаграммы фазового равновесия для воды и диоксида углерода (С0₂) — веществ, имеющих большое практическое значение в пищевых производствах.

Рис. 3.5. Диаграмма фазового равновесия воды

Рис. 3.6. Диаграмма фазового равновесия С0₂

Следует знать, что в случае воды далеко за пределами диаграммы, при сверхвысоких давлениях, есть несколько переходов между твердыми фазами, где одна форма кристаллической решетки превращается в другую. Некоторые из этих форм льда (они называются лед-Н, -III, -V, -VI и -VII, существование льда IV не подтвердилось) имеют высокие температуры плавления. Например, лед VII плавится при 100°С, но существует он при давлениях, превышающих 25 000 атм.

В случае С0₂ фазовая диаграмма имеет ту особенность, что атмосферное давление приходится на равновесие тв г, а это означает, что нагрев твердого диоксида углерода (сухого льда) на открытом воздухе приводит к его сублимации — он, минуя жидкость, превращается в газ. Это свойство сухого льда используют при охлаждении продуктов питания (например, мороженого). Нетрудно представить себе, какие хлопоты имели бы продавцы, если бы при нагревании сухой лед, как и обычный, превращался сначала в жидкость. Чтобы все же получить жидкую углекислоту, нужно «плавить» сухой лед при давлениях, превышающих 5,11 атм (давление в тройной точке).

Видео:Фазовые диаграммы. Тройная точка. Критическое состояние вещества. 10 класс.Скачать

Фазовые равновесия. Правило фаз Гиббса. Классификация систем. Фазовые равновесия в однокомпонентных системах. Уравнение Клапейрона-Клаузиуса. Диаграммы состояния однокомпонентных систем.

Фазовые равновесия. Правило фаз Гиббса. Классификация систем. Фазовые равновесия в однокомпонентных системах. Уравнение Клапейрона-Клаузиуса. Диаграммы состояния однокомпонентных систем.

ФАЗОВЫЕ РАВНОВЕСИЯ. ПРАВИЛО ФАЗ ГИББСА.

Фазой называется гомогенная часть гетерогенной системы, имеющая во всех точках одинаковые значения интенсивных параметров, которые изменяются скачком на границе раздела фаз.

Фазовым переходом называется переход вещества из одной фазы в другую.

Фазовыми равновесиями называют равновесия в гетерогенных системах, в которых имеют место только фазовые переходы и отсутствуют химические взаимодействия между компонентами.

При переходе из одной фазы (1) в другую фазу (2) dn_i молей i–ого компонента (например, при конденсации пара или кристаллизации осадка), энергия Гиббса каждой из фаз изменится на величину:

для фазы 1 ,

для фазы 2 .

Общее изменение энергии Гиббса равно:

. (1)

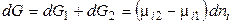
Если переход происходит в условиях равновесия при T, р = const, то

, и .

Этот вывод распространяется на любой компонент и на любую фазу системы. Итак, равновесию гетерогенных систем отвечает равенство химических потенциалов каждого компонента во всех фазах при T, p = const. Если же химический потенциал некоторого вещества в одной фазе (в одном растворе) будет больше, чем в другой фазе (в другом растворе), то вещество будет самопроизвольно переходитьиз первой фазы в другую.

Рассмотрим систему, содержащую К компонентов и состоящую из Ф фаз, находящихся в равновесии между собой. Состав каждой из фаз определяется концентрациями (К – 1) компонентов, а так как число всех фаз равно Ф, то состав всей системы определится Ф(К – 1) концентрациями всех компонентов. Для полного описания состояния системы необходимы ещё температура и давление, т. е. всего Ф (К – 1) + 2 переменных.

Условием равновесия гетерогенной системы из Ф фаз и К компонентов (как отмечалось ранее) является постоянство температуры и давления, а также равенство всех химических потенциалов каждого из компонентов во всех фазах:

. , (2)

. . (3)

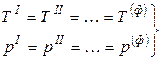
Здесь верхние индексы обозначают номера фаз, нижние индексы относятся к соответствующим компонентам.

В вышеприведенных равенствах каждое значение m является функцией температуры, давления и концентрации всех компонентов. Например, для двухкомпонентной системы:

Следовательно, каждое равенство из (4.3) (например ) даёт уравнение, связывающее переменные системы. Эти уравнения уменьшают число независимых переменных, характеризующих систему, и называются уравнениями связей.

Обозначим через f число действительно независимых переменных. Тогда

, (4)

. (5)

Последнее соотношение было получено Дж. Гиббсом и носит название уравнения (правила фаз) Гиббса. Равновесные гетерогенные системы, состоящие из любого числа фаз и любого числа веществ, подчиняются правилу фаз Гиббса. Его можно сформулировать следующим образом:

число степеней свободы равновесной термодинамической системы, на которую из внешних факторов влияют только давление и температура, равно числу компонентов системы плюс два, минус число фаз:

где К — число компонентов – веществ, наименьшее число которых необходимо и достаточно для образования всех возможных фаз данной равновесной системы. Компонент является составной частью системы и может быть выделен из нее, и существовать самостоятельно;

f — число степеней свободы – число независимых термодинамических параметров, определяющих состояние системы, изменение которых в определенных пределах не вызывает исчезновения одних и образование других фаз;

число 2 — это число внешних факторов (Р и Т), которые влияют на равновесие.

Перепишем уравнение (4.5) в виде

, (6)

тогда при находим, что

, (7)

т.е. максимальное число фаз в гетерогенной системе при равновесии равно числу компонентов плюс два.

Если р или Т = const, то правило фаз Гиббса запишется как

КЛАССИФИКАЦИЯ СИСТЕМ.

Можно подразделять системы по числу компонентов, степеней свободы и по числу фаз.

1). По числу компонентов ситемы классифицируют как

– однокомпонентные (или одинарные);

– двухкомпонентные (или двойные);

– трёхкомпонентные (или тройные) и т. д.

2). По числу фаз системы классифицируют как

– трёхфазные и т. д.

3). По числу степеней свободы (вариантности) системы классифицируют как

– безвариантные или нонвариантные ( f = 0);

– одновариантные или моновариантные ( f = 1);

– двухвариантные или бивариантные ( f = 2) и т. д.

Число компонентов определяют как наименьшее число составляющих частей системы, достаточное для образования всех её фаз. Число компонентов не равно числу составляющих частей лишь в тех случаях, когда между ними происходят химические взаимодействия (реакции) и в системе устанавливается химическое равновесие. В этом случае число компонентов равно числу составляющих частей системы минус число уравнений, связывающих концентрации составляющих частей.

Растворы, их общая характеристика, способы выражения состава растворов. Растворимость твердых веществ и газов в жидкостях. Идеальные растворы, законы Вант-Гоффа, Рауля и Генри. Криоскопия и эбулиоскопия. Диаграммы состояния раствор — пар для бинарных систем. Законы Коновалова, азеотропные смеси. Ограниченная взаимная растворимость жидкостей. Взаимно нерастворимые жидкости. Распределение вещества в двух несмешивающихся растворителях. Закон распределения Нернста-Шилова.

Растворы классифицируют

1). по степени дисперсности на

— истинные (молекулярные или атомные смеси компонентов);

— тонкие механические взвеси (суспензии и эмульсии).

2). по агрегатному состоянию на

3. с термодинамических позиций на

— предельно разбавленые (С₂ → 0);

Физическая химия изучает термодинамические и другие свойства растворов. Коллоидные растворы и тонкие механические взвеси являются предметом исследования коллоидной химии. Свойства растворителя обычно обозначаются индексом (1), а свойства растворенных веществ – индексами (2), (3) и т. д.

Способы выражения состава растворов.

Так как количество каждого компонента может быть представлено в различных единицах измерения, то и состав раствора можно выразить несколькими способами.

1). Через мольные (молярные) доли x_i:

, , (1)

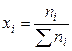
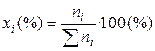
где n_i – число молей i-го компонента в растворе.

2). Через объёмные доли j_i:

, , (2)

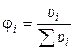
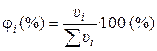
где u_i ‑ объём i-ого компонента в объёме раствора u.

3). Через массовые доли :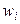

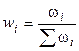
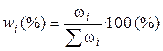
, , (3)

где ω_i – масса i-ого компонента в растворе.

4). Через молярные концентрации (молярности) С_i:

(моль/л), (4)

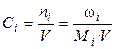
где ω_i – масса i-го компонента (г), М_i – молярная масса i-ого компонента (г/моль), V – объём раствора (л), n_i – число молей.

5). Через моляльные концентрации (моляльности) m_i:

(моль/кг). (5)

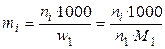
Моляльность выражает число молей i-ого компонента (растворенного вещества) в расчете на 1 кг растворителя.

6) Через молярные концентрации эквивалента (эквивалентные концентрации, нормальности) – С_i или N_i:

(моль·г-экв/л), (6)

где фактор эквивалентности f_экв показывает, какая доля молярной массы данного вещества эквивалентна одному иону водорода в данной окислительно – восстановительной реакции.

Закон Генри.

Предельно разбавленными называются такие растворы, в которых молярная доля растворенного вещества x₂ (T, x_i) которую Дж. Льюис назвал термодинамической активностью i-ого компонента в растворе. В связи с этим для реальных растворов будут иметь место два равенства:

, (39)

если пар подчиняется законам идеальных газов, и

, (40)

если рассматривать пар как реальный газ. Активность связана с мольной долей компонента через коэффициент активности :

. (41)

Величина коэффициента активности указывает на величину отклонения реальных растворов от идеальности (законов идеальных растворов).

Фазовые равновесия в однокомпонентных системах уравнение клапейрона клаузиуса

Если давление насыщенного пара над реальным раствором больше, чем над идеальным раствором того же состава (g_i > 1), то отклонения от идеальности называются положительными. Если давление насыщенного пара над реальным раствором меньше, чем над идеальным раствором того же состава (g_i

Что способствует осуществлению желаний? Стопроцентная, непоколебимая уверенность в своем.

ЧТО ПРОИСХОДИТ, КОГДА МЫ ССОРИМСЯ Не понимая различий, существующих между мужчинами и женщинами, очень легко довести дело до ссоры.

Система охраняемых территорий в США Изучение особо охраняемых природных территорий(ООПТ) США представляет особый интерес по многим причинам.

Что вызывает тренды на фондовых и товарных рынках Объяснение теории грузового поезда Первые 17 лет моих рыночных исследований сводились к попыткам вычислить, когда этот.

Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:

Видео:Фазовые равновесия | ФизхимияСкачать

Клапейрона–Клаузиуса

ТЕПЛОВЫЕ ЭФФЕКТЫ ФАЗОВЫХ ПЕРЕХОДОВ.

УРАВНЕНИЕ КЛАПЕЙРОНА – КЛАУЗИУСА.

Переход компонента из одной фазы в другую сопровождается выделением или поглощением теплоты, которую можно определить количественно на основе фундаментального уравнения термодинамики:

(*)

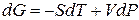
ВЫВОД И АНАЛИЗ УРАВНЕНИЯ КЛАПЕЙРОНА – КЛАУЗИУСА.

Для любого равновесного перехода вещества из одной фазы α в другую фазу β, применяя уравнение (*) к каждой из фаз, можно написать

Индексы α и β отражают принадлежность параметров к соответствующей фазе. В равновесных условиях между фазами α и β изменение энергии Гиббса отсутствует, т.е.

Приравнивая правые части уравнений 1 и 2, получим

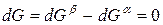
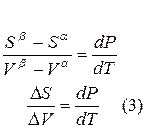
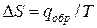
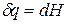
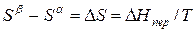
Для равновесного обратимого процесса согласно уравнениям и запишем

а уравнение (3) примет вид

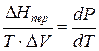
где ∆H_пер – теплота фазового перехода.

Тепловой эффект, сопровождающий фазовый переход, определяется следующим образом:

уравнение

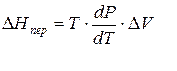
Клапейрона–Клаузиуса

где ∆V – изменение объема в результате фазового перехода; dP/dT – изменение давления в зависимости от температуры при сохранении равновесия между двумя фазами.

Уравнение Клапейрона–Клаузиуса связывает тепловой эффект процесса с изменением давления насыщенного пара, температурой и изменением объема в процессе фазового перехода.

Для процессов испарения ж→п и сублимации тв→п уравнение Клапейрона–Клаузиуса можно представить следующим образом:

где ∆H_исп , ∆H_суб – теплоты испарения и сублимации; V_п, V_ж, V_тв – мольные объемы пара, жидкости и твердого тела соответственно.

В процессе испарения и сублимации наблюдается значительное изменение удельного объема ∆V и существенное изменение величины dP/dT. При плавлении, напротив, изменение ∆V невелико, и величина dP/dT незначительна.

Пример 1. Проведем расчет по уравнению Клапейрона–Клаузиуса температуры плавления фенола Т_пл. Плотность твердого фенола ρ_тв при атмосферном давлении составляет 1,072∙10 3 кг/м 3 , а жидкого ρ_ж = 1,056∙10 3 кг/м 3 ; теплота плавления ∆H_пл = 1,045∙10 5 Дж/кг; температура замерзания 314,2 К. Определим dP/dT и температуру плавления при Р = 5,065∙10 7 Па:

Прирост температуры плавления при повышении давления на 1 атм ( 1,013∙10 5 Па) составляет 4,525∙10 -8 град/Па. При увеличении давления до 5,065∙10 7 Па температура плавления увеличивается на ∆T = (dT/dP)∆P = 4,525∙10 -8 ∙ 5,065∙10 7 = 2,29 К, т.е. составит Т_пл = 314,2+2,29 = 316,49 К.

Следует иметь в виду, что в процессе плавления у большинства веществ V_ж > V_{тв ,} тогда ∆V>0 и при повышении давления Р↑ температура плавления повышается Т↑.

Однако, такие вещества как вода (Н₂О), висмут (Bi), имеют объем твердой фазы V_тв больше, чем объем жидкой фазы V_ж уд = 10 -3 м 3 /кг и V_тв уд = 1,091·10 -3 м 3 /кг; теплота плавления ∆H_пл = 332,4 кДж/кг:

Это значение показывает, что для понижения температуры таяния льда на один градус Кельвина необходимо увеличить давление на 1,34∙10 7 Па, т.е. примерно на 134 атмосферы, что нереально, поскольку такое давление лед не выдерживает – трескается.

Таяние льда происходит в основном в результате трения и превращения работы в теплоту при скольжении конька по льду, а не за счет повышения давления на лед.

Уравнение для процесса испарения 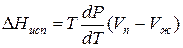можно представить в интегральном виде. Мольный объем пара значительно превосходит мольный объем жидкости, V_п >> V_{ж ,} т.е. величиной V_ж можно пренебречь. Тогда уравнение Клапейрона–Клаузиуса запишется в виде:

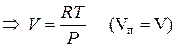
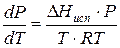
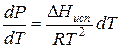
Пар подчиняется законам идеального газа: PV=RT , тогда , преобразуем уравнение, переставляя давление Р в левую часть уравнения, а dT в правую часть. Получаем:

или

Проведем интегрирование уравнения (1) в пределах от Т₁ до Т₂ и соответственно от Р₁ до Р₂ при условии, что в области невысоких давлений пара ∆Н_исп ≈ const; в результате интегрирования получим:

∆Н_исп / R = const, выносим за знак интеграла

При помощи уравнения (2) можно графически определить значения теплоты испарения, если известны давления Р₁ и Р₂ и соответствующие им температуры испарения Т₁ и Т₂ . Для этого необходимо отложить на оси абсцисс значения обратной температуры, а на оси ординат – lnP.

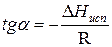
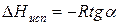
Зависимость lnP от 1/Т будет линейной, а тангенс угла наклона этой прямой равен , т.е. , а

Расчетные значения ∆Н_исп получаются с достаточной для практики точностью, не уступающей точности непосредственного измерения. Возможно использование уравнения (2) для обратного расчета, когда по значению ∆Н_исп определяют изменение давления при изменении температуры в процессе испарения.

Теплоту фазовых переходов можно определить и по величине стандартной энтальпии образования, в зависимости от фазового состояния продуктов реакции.

Пример. Лучше всего это показать на примере теплоты образования воды из газообразных кислорода и водорода, которая составляет

для водяного пара ∆Н_(г) 0 = -241,82 кДж/моль; для воды в жидком состоянии ∆Н_(ж) 0 = -285,83 кДж/моль; для льда ∆Н_(тв) 0 = -291,82 кДж/моль. Теплота конденсации воды равна:

а теплота превращения воды в лед:

Как видно, тепловой эффект фазовых переходов значительно меньше теплоты образования веществ.

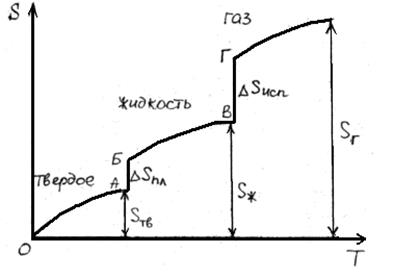
В результате фазовых переходов происходит изменение энтропии. Такие изменения в зависимости от температуры представим на рисунке.

Как известно, энтропия идеального кристалла при абсолютном нуле равна нулю. С ростом температуры атомы (ионы) флуктуировать относительно равновесного положения, число возможных способов их размещения растет, и энтропия увеличивается (ΔS>0). При достижении температуры плавления (точка А на рисунке) кристаллическая решетка разрушается скачкообразно (отрезок АБ), увеличивается термодинамическая вероятность системы W, а в соответствии с формулой S=k∙lnW (где k – постоянная Больцмана) энтропия при переходе от твердого в жидкое состояние растет. Более значительный скачок энтропии имеет место при переходе из жидкого состояния в газообразное (отрезок ВГ), когда ближний порядок расположения частиц друг относительно друга нарушается, и движение частиц становится хаотичным.

Пример. Оценим скачок энтропии на примере фазовых переходов воды:

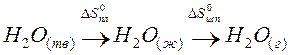
когда известны стандартные абсолютные значения энтропии S_тв 0 =39,4; S_ж 0 =69,9; S_г 0 =188,7 Дж/(моль·К).

В соответствии с рисунком для воды

По известной энтальпии фазового перехода можно рассчитать изменение энтропии в соответствии с формулой

Пример.Вычислим изменение энтропии в процессе парообразования 1 моля этилхлорида при 12,3 0 С, когда теплота испарения ∆Н_исп =24,16 кДж/моль.

Молекулярная масса 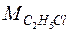= 64,5 г/моль.

В заключение отмечу, что мы рассматривали лишь фазовые переходы I рода. При фазовых переходах I рода свойства веществ, выражаемые, например, через химический потенциал, первыми производными одной из характеристических функций, изменяются скачком при непрерывном изменении соответствующих параметров: температуры, давления, объема и энтропии. При этом выделяется или поглощается теплота перехода ∆Н_пер в соответствии с уравнением Клапейрона–Клаузиуса.

Кроме них, однако, существуют фазовые переходы II рода. Они не сопровождаются выделением или поглощением теплоты, для них уравнение Клапейрона–Клаузиуса теряет смысл. Эти переходы характеризуют изменения в системе, которые не определяются объемом и запасом энергии. В этом случае первые производные одной из характеристических функций непрерывны, а вторые производные (например, теплоемкость) изменяются скачком. К фазовым переходам II рода относятся переходы парамагнетика в ферромагнетик, диэлектрика в сегнетоэлектрик, а также процессы возникновения сверхтекучести, сверхпроводимости и др.

В настоящее время насчитывается около 400 твердых минералов, для которых наблюдаются фазовые переходы II рода: рутил, анатаз, алмаз и особенно кварц, который имеет семь модификаций, причем наряду с фазовыми переходами I рода наблюдаются фазовые переходы II рода. Так, при 573 0 С и переходе модификации кварца β 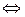α теплоемкость и коэффициент линейного расширения изменяются скачкообразно (I род), но при этом поглощается теплота 10,9 кДж/моль (II род).

\|	следующая лекция ==>
ДИАГРАММА СОСТОЯНИЯ СЕРЫ.	\|	ХАРАКТЕРИСТИКА И СВОЙСТВА РАСТВОРОВ.

Дата добавления: 2016-02-02 ; просмотров: 3225 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ