- Лаборатория автоматизации и цифровой обработки сигналов
- Построение фазовых портретов на языке Python
- Шаг 1. Реализация ОДУ в Python
- Шаг 2. Численное решение ОДУ
- Шаг 3. Генерация и вывод фазового портрета
- Шаг 4. Запуск построения
- Julia и фазовые портреты динамических систем
- Осциллятор
- Брюсселятор
- Как построить фазовый портрет в python
- Digiratory
- Лаборатория автоматизации и цифровой обработки сигналов
- Построение фазовых портретов на языке Python
- Шаг 1. Реализация ОДУ в Python
- Шаг 2. Численное решение ОДУ
- Шаг 3. Генерация и вывод фазового портрета
- Шаг 4. Запуск построения
- Фазовый портрет сигнала по точкам
- Julia и фазовые портреты динамических систем
- Осциллятор
- Брюсселятор
- 📹 Видео
Видео:Асташова И. В. - Дифференциальные уравнения. Часть 2 - Фазовый портретСкачать

Лаборатория автоматизации и цифровой обработки сигналов
Видео:Python - численное решение дифференциального уравнения 1го порядка и вывод графикаСкачать

Построение фазовых портретов на языке Python
Фазовая траектория — след от движения изображающей точки. Фазовый портрет — это полная совокупность различных фазовых траекторий. Он хорошо иллюстрирует поведение системы и основные ее свойства, такие как точки равновесия.
С помощью фазовых портретов можно синтезировать регуляторы (Метод фазовой плоскости) или проводить анализ положений устойчивости и характера движений системы.
Рассмотрим построение фазовых портретов нелинейных динамических систем, представленных в форме обыкновенных дифференциальных уравнений
В качестве примера воспользуемся моделью маятника с вязким трением:
Где (omega ) — скорость, (theta ) — угол отклонения, (b ) — коэффициент вязкого трения, (с ) — коэффициент, учитывающий массу, длину и силу тяжести.
Для работы будем использовать библиотеки numpy, scipy и matplotlib для языка Python.
Блок импорта выглядит следующим образом:
Видео:Дополнительные главы ИДУ: Построение фазовых портретов | Занятие 3Скачать

Шаг 1. Реализация ОДУ в Python
Определим функцию, отвечающую за расчет ОДУ. Например, следующего вида:
Аргументами функции являются:
- y — вектор переменных состояния
- t — время
- b, c — параметры ДУ (может быть любое количество)
Функция возвращает вектор производных.
Видео:Python - поле направлений дифференциального уравненияСкачать

Шаг 2. Численное решение ОДУ
Далее необходимо реализовать функцию для получения решения ОДУ с заданными начальными условиями:
Аргументами функции являются:
- args — Параметры ОДУ (см. шаг 1)
- y0— Начальные условия для первой переменной состояния
- dy0 — Начальные условия для второй переменной состояния (или в нашем случае ее производной)
- ts — длительность решения
- nt — Количество шагов в решении (= время интегрирования * шаг времени)
В 3-й строке формируется вектор временных отсчетов. В 4-й строке вызывается функция решения ОДУ.
Видео:Решение дифференциальных уравнений. Построение фазового портрета систему ДУ. Урок 47Скачать

Шаг 3. Генерация и вывод фазового портрета
Для построения фазового портрета необходимо произвести решения ОДУ с различными начальными условиями (вокруг интересующей точки). Для реализации также напишем функцию.
Аргументами функции являются:
- args — Параметры ОДУ (см. шаг 1)
- deltaX — Шаг начальных условий по горизонтальной оси (переменной состояния)
- deltaDX — Шаг начальных условий по вертикальной оси (производной переменной состояния)
- startX — Начальное значение интервала начальных условий
- stopX — Конечное значение интервала начальных условий
- startDX — Начальное значение интервала начальных условий
- stopDX — Конечное значение интервала начальных условий
- ts — длительность решения
- nt — Количество шагов в решении (= время интегрирования * шаг времени)
Во вложенных циклах (строки 3-4) происходит перебор начальных условий дифференциального уравнения. В теле этих циклов (строки 5-6) происходит вызов функции решения ОДУ с заданными НУ и вывод фазовая траектории полученного решения.
Далее производятся нехитрые действия:
- Строка 7 — задается название оси X
- Строка 9 — задается название оси Y
- Строка 10 — выводится сетка на графике
- Строка 11 — вывод графика (рендер)
Видео:01.02. Модель SIR. Численное решение системы дифференциальных уравнений с помощью SciPyСкачать

Шаг 4. Запуск построения
Запустить построение можно следующим образом:
Строка 1-2 — задание значений параметрам ОДУ
Строка 3 — формирование вектора параметров
Строка 4 — вызов функции генерации фазового портрета с параметрами «по умолчанию»
Строка 5 — вызов функции генерации фазового портрета с настроенными параметрами
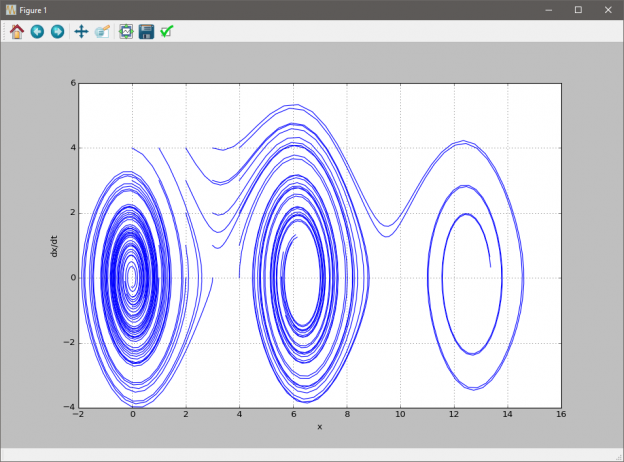
При запуске программы получаем следующий результат:
Полный текст программы под лицензией MIT (Использование при условии ссылки на источник):
Видео:Дифференциальные уравнения 6. Фазовые траектории. Особые точки автономных системСкачать

Julia и фазовые портреты динамических систем
Продолжаем осваивать молодой и перспективный язык общего назначения Julia. Но для начала нам нужна как раз таки сугубо узкая возможность применения — для решения типичных задач физики. Это самая удобная тактика освоения инструмента: чтоб набить руку, будем решать насущные проблемы, постепенно увеличивая сложность и находя способы облегчения своей жизни. Короче, будем решать дифуры и строить графики.
Для начала качаем графический пакет Gadfly, да сразу полную версию разработчика, чтоб хорошо работала с нашей Julia 1.0.1. Вбиваем в нашем REPL, JUNO или Jupyter notebook:
Не самый удобный вариант, но пока ждём обновления PlotlyJS можно ради сравнения и попробовать.
Также нужен могущественнейший инструмент для решения дифференциальных уравнений DifferentialEquations
Это самый обширный и поддерживаемый пакет, предоставляющий уйму методов решения дифуров. Теперь приступим к фазовым портретам.
Решения обыкновенных дифференциальных уравнений часто удобнее изображать не в привычном виде , а в фазовом пространстве, по осям которого откладываются значения каждой из найденных функций. При этом аргумент t входит в графики лишь параметрически. В случае двух ОДУ такой график – фазовый портрет системы, является кривой на фазовой плоскости и поэтому особенно нагляден.
Осциллятор
Динамика гармонического осциллятора с затуханием описывается следующей системой уравнений:
и независимо от начальных условий (х0, у0), приходит в состояние равновесия, точку (0,0) с нулевым углом отклонения и нулевой скоростью.
При решение принимает вид свойственный для классического осциллятора.
Разберем код. Функция принимает значения частоты и параметра затухания, а также начальные условия. Вложенная функция syst() задает систему. Для того чтоб вышло однострочно воспользовались матричным умножением. Функция solve() принимая огромное количество параметров весьма гибко настраивается для решения проблемы, но мы лишь указали метод решения — Рунге-Кутты 4 (есть ещё много других), относительную погрешность, и то, что надо сохранять не все точки, а только каждую четвертую. В переменную sol сохраняется матрица-ответ, причем, sol.t содержит вектор значений времен, а sol.u решения системы на этих временах. Все это спокойно рисуется в Plots, а для Gadfly придется укомплектовывать ответ в матрицу поудобней. Времена нам не нужны, так что возвращаем только решения.
Построим фазовый портрет:
Среди функций высокого порядка для нас особенно приметна broadcast(f, [1, 2, 3]) , которая в функцию f поочередно подставляет значения массива [1, 2, 3]. Краткая запись f.([1, 2, 3]) . Это пригодится чтобы поварьировать частоту, параметр затухания, начальную координату и начальную скорость.
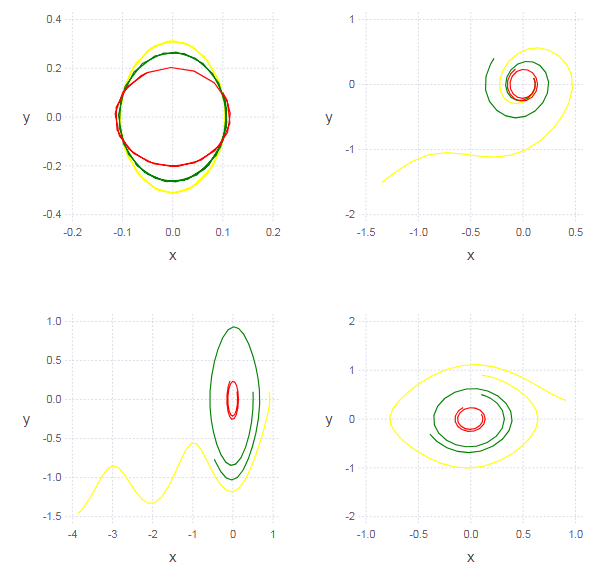
Теперь рассмотрим не малые колебания, а колебания произвольной амплитуды:
График решения на фазовой плоскости не является эллипсом (что говорит о нелинейности осциллятора). Чем меньше мы будем выбирать амплитуду колебаний (т.е. начальные условия), тем меньше будет проявляться нелинейность (поэтому-то малые колебания маятника можно считать гармоническими).
Брюсселятор
Эта модель описывает некоторую автокаталитическую химическую реакцию, в которой определенную роль играет диффузия. Модель была предложена в 1968 г. Лефевром и Пригожиным
Неизвестные функции отражают динамику концентрации промежуточных продуктов химической реакции. Параметр модели
имеет смысл исходной концентрации катализатора (третьего вещества).
Более детально, эволюцию фазового портрета брюсселятора можно наблюдать, проводя расчеты с различным параметром . При его увеличении узел будет сначала постепенно смещаться в точку с координатами (1,
), пока не достигнет бифуркационного значения
=2. В этой точке происходит качественная перестройка портрета, выражающаяся в рождении предельного цикла. При дальнейшем увеличении
происходит лишь количественное изменение параметров этого цикла.
На сегодня достаточно. В следующий раз попробуем научиться пользоваться другим графическим пакетом на новых задачах, попутно набивая руку на синтаксис Юлии. В процессе решения задач потихоньку начинают прослеживаться не то чтобы прям плюсы и минусы… скорее приятности и неудобства — этому следует посвятить отдельный разговор. И конечно хотелось бы на хабре увидеть что-то посерьезней моих игр с функциями — посему призываю джулистов поопытней рассказать о более менее серьезных проектах, это помогло бы многим и мне в частности, в изучении этого замечательного языка.
Видео:ТАУ. Matlab/SIMULINK Фазовые портреты систем нелинейных диф. уравненийСкачать

Как построить фазовый портрет в python
Видео:Решение ОДУ в PythonСкачать

Digiratory
Лаборатория автоматизации и цифровой обработки сигналов
Видео:Устойчивость 1 ОпределениеСкачать

Построение фазовых портретов на языке Python
Фазовая траектория — след от движения изображающей точки. Фазовый портрет — это полная совокупность различных фазовых траекторий. Он хорошо иллюстрирует поведение системы и основные ее свойства, такие как точки равновесия.
С помощью фазовых портретов можно синтезировать регуляторы (Метод фазовой плоскости) или проводить анализ положений устойчивости и характера движений системы.
Рассмотрим построение фазовых портретов нелинейных динамических систем, представленных в форме обыкновенных дифференциальных уравнений
В качестве примера воспользуемся моделью маятника с вязким трением:
Где (omega ) — скорость, (theta ) — угол отклонения, (b ) — коэффициент вязкого трения, (с ) — коэффициент, учитывающий массу, длину и силу тяжести.
Для работы будем использовать библиотеки numpy, scipy и matplotlib для языка Python.
Блок импорта выглядит следующим образом:
Видео:#5. Математические функции и работа с модулем math | Python для начинающихСкачать

Шаг 1. Реализация ОДУ в Python
Определим функцию, отвечающую за расчет ОДУ. Например, следующего вида:
Аргументами функции являются:
- y — вектор переменных состояния
- t — время
- b, c — параметры ДУ (может быть любое количество)
Функция возвращает вектор производных.
Видео:ТАУ. Matlab/SIMULINK Фазовые портреты нелинейных и линейных диф. уравненийСкачать

Шаг 2. Численное решение ОДУ
Далее необходимо реализовать функцию для получения решения ОДУ с заданными начальными условиями:
Аргументами функции являются:
- args — Параметры ОДУ (см. шаг 1)
- y0— Начальные условия для первой переменной состояния
- dy0 — Начальные условия для второй переменной состояния (или в нашем случае ее производной)
- ts — длительность решения
- nt — Количество шагов в решении (= время интегрирования * шаг времени)
В 3-й строке формируется вектор временных отсчетов. В 4-й строке вызывается функция решения ОДУ.
Видео:Асташова И. В. - Дифференциальные уравнения. Часть 2 - Лекция 11Скачать

Шаг 3. Генерация и вывод фазового портрета
Для построения фазового портрета необходимо произвести решения ОДУ с различными начальными условиями (вокруг интересующей точки). Для реализации также напишем функцию.
Аргументами функции являются:
- args — Параметры ОДУ (см. шаг 1)
- deltaX — Шаг начальных условий по горизонтальной оси (переменной состояния)
- deltaDX — Шаг начальных условий по вертикальной оси (производной переменной состояния)
- startX — Начальное значение интервала начальных условий
- stopX — Конечное значение интервала начальных условий
- startDX — Начальное значение интервала начальных условий
- stopDX — Конечное значение интервала начальных условий
- ts — длительность решения
- nt — Количество шагов в решении (= время интегрирования * шаг времени)
Во вложенных циклах (строки 3-4) происходит перебор начальных условий дифференциального уравнения. В теле этих циклов (строки 5-6) происходит вызов функции решения ОДУ с заданными НУ и вывод фазовая траектории полученного решения.
Далее производятся нехитрые действия:
- Строка 7 — задается название оси X
- Строка 9 — задается название оси Y
- Строка 10 — выводится сетка на графике
- Строка 11 — вывод графика (рендер)
Видео:Откуда появляются дифференциальные уравнения и как их решатьСкачать

Шаг 4. Запуск построения
Запустить построение можно следующим образом:
Строка 1-2 — задание значений параметрам ОДУ
Строка 3 — формирование вектора параметров
Строка 4 — вызов функции генерации фазового портрета с параметрами «по умолчанию»
Строка 5 — вызов функции генерации фазового портрета с настроенными параметрами
При запуске программы получаем следующий результат:
Полный текст программы под лицензией MIT (Использование при условии ссылки на источник):
Видео:Консультация по дифференциальным уравнениям №2, часть 3Скачать

Фазовый портрет сигнала по точкам

Добрый день. Стоит следующая задача: дана система из трех ДУ. Нужно решить ее численно методом.
Фазовый портрет
Добрый день. Раньше не пользовалась мэпл 13, но захотелось построить график покрасивще, чем от.

Вообщем дана такая система уравнений: left dot & = & x, -, 3y \ .
Построить фазовый портрет
Помогите пожалуйста построить фазовый портрет. Делаю по примеру, но график не строит. У меня.
Может имеется ввиду АФЧХ?
Сделали fft и стройте зависимость мнимой части от действительной.
Добавлено через 10 минут
Т.е. изображаете точки на комплексной плоскости.
Видео:Видеоурок "Системы дифференциальных уравнений"Скачать

Julia и фазовые портреты динамических систем
Продолжаем осваивать молодой и перспективный язык общего назначения Julia. Но для начала нам нужна как раз таки сугубо узкая возможность применения — для решения типичных задач физики. Это самая удобная тактика освоения инструмента: чтоб набить руку, будем решать насущные проблемы, постепенно увеличивая сложность и находя способы облегчения своей жизни. Короче, будем решать дифуры и строить графики.
Для начала качаем графический пакет Gadfly, да сразу полную версию разработчика, чтоб хорошо работала с нашей Julia 1.0.1. Вбиваем в нашем REPL, JUNO или Jupyter notebook:
Не самый удобный вариант, но пока ждём обновления PlotlyJS можно ради сравнения и попробовать.
Также нужен могущественнейший инструмент для решения дифференциальных уравнений DifferentialEquations
Это самый обширный и поддерживаемый пакет, предоставляющий уйму методов решения дифуров. Теперь приступим к фазовым портретам.
Решения обыкновенных дифференциальных уравнений часто удобнее изображать не в привычном виде , а в фазовом пространстве, по осям которого откладываются значения каждой из найденных функций. При этом аргумент t входит в графики лишь параметрически. В случае двух ОДУ такой график – фазовый портрет системы, является кривой на фазовой плоскости и поэтому особенно нагляден.
Осциллятор
Динамика гармонического осциллятора с затуханием описывается следующей системой уравнений:
и независимо от начальных условий (х0, у0), приходит в состояние равновесия, точку (0,0) с нулевым углом отклонения и нулевой скоростью.
При решение принимает вид свойственный для классического осциллятора.
Разберем код. Функция принимает значения частоты и параметра затухания, а также начальные условия. Вложенная функция syst() задает систему. Для того чтоб вышло однострочно воспользовались матричным умножением. Функция solve() принимая огромное количество параметров весьма гибко настраивается для решения проблемы, но мы лишь указали метод решения — Рунге-Кутты 4 (есть ещё много других), относительную погрешность, и то, что надо сохранять не все точки, а только каждую четвертую. В переменную sol сохраняется матрица-ответ, причем, sol.t содержит вектор значений времен, а sol.u решения системы на этих временах. Все это спокойно рисуется в Plots, а для Gadfly придется укомплектовывать ответ в матрицу поудобней. Времена нам не нужны, так что возвращаем только решения.
Построим фазовый портрет:
Среди функций высокого порядка для нас особенно приметна broadcast(f, [1, 2, 3]) , которая в функцию f поочередно подставляет значения массива [1, 2, 3]. Краткая запись f.([1, 2, 3]) . Это пригодится чтобы поварьировать частоту, параметр затухания, начальную координату и начальную скорость.
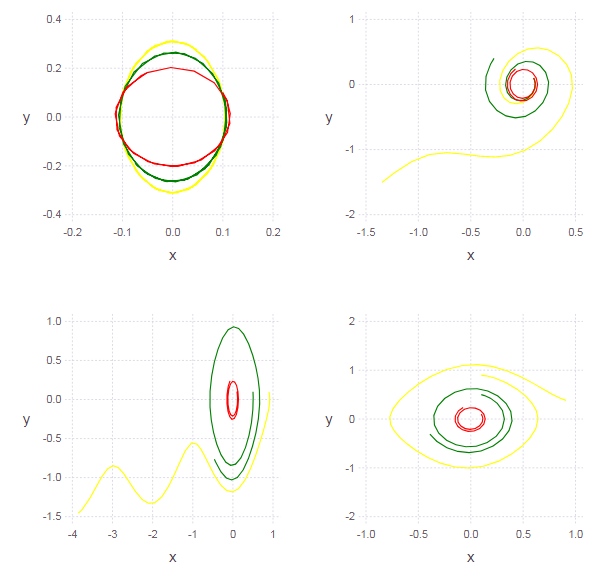
Теперь рассмотрим не малые колебания, а колебания произвольной амплитуды:
График решения на фазовой плоскости не является эллипсом (что говорит о нелинейности осциллятора). Чем меньше мы будем выбирать амплитуду колебаний (т.е. начальные условия), тем меньше будет проявляться нелинейность (поэтому-то малые колебания маятника можно считать гармоническими).
Брюсселятор
Эта модель описывает некоторую автокаталитическую химическую реакцию, в которой определенную роль играет диффузия. Модель была предложена в 1968 г. Лефевром и Пригожиным
Неизвестные функции отражают динамику концентрации промежуточных продуктов химической реакции. Параметр модели имеет смысл исходной концентрации катализатора (третьего вещества).
Более детально, эволюцию фазового портрета брюсселятора можно наблюдать, проводя расчеты с различным параметром . При его увеличении узел будет сначала постепенно смещаться в точку с координатами (1, ), пока не достигнет бифуркационного значения =2. В этой точке происходит качественная перестройка портрета, выражающаяся в рождении предельного цикла. При дальнейшем увеличении происходит лишь количественное изменение параметров этого цикла.
На сегодня достаточно. В следующий раз попробуем научиться пользоваться другим графическим пакетом на новых задачах, попутно набивая руку на синтаксис Юлии. В процессе решения задач потихоньку начинают прослеживаться не то чтобы прям плюсы и минусы… скорее приятности и неудобства — этому следует посвятить отдельный разговор. И конечно хотелось бы на хабре увидеть что-то посерьезней моих игр с функциями — посему призываю джулистов поопытней рассказать о более менее серьезных проектах, это помогло бы многим и мне в частности, в изучении этого замечательного языка.
📹 Видео
Кулешов А. С. - Теоретическая механика. Семинары - Фазовые портретыСкачать