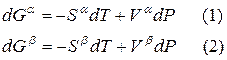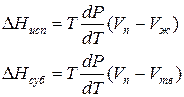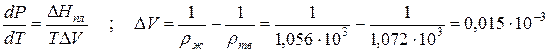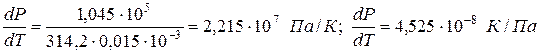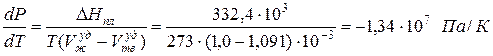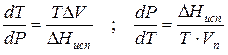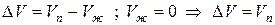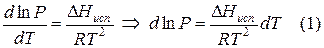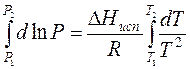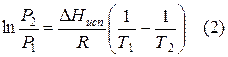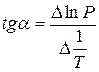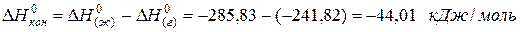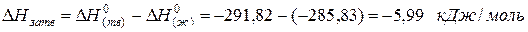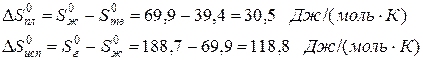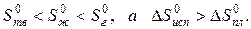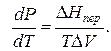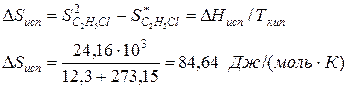Фазовые переходы уравнение клапейрона клаузиуса (4 видео)

Содержание

Клапейрона–Клаузиуса
Физическая химия
Главная > Документ
§ 3. Фазовые переходы. Уравнение Клапейрона-Клаузиуса
§ 4. Фазовые переходы первого рода. Плавление. Испарение
§ 5. Зависимость давления насыщенного пара от температуры
§ 6. Сверхкритическое состояние вещества.
КЛАПЕЙРО́НА – КЛА́УЗИУСА УРАВНЕ́НИЕ
🔥 Видео

Видео:Урок 194. Уравнение Ван-дер-ВаальсаСкачать

Клапейрона–Клаузиуса

ТЕПЛОВЫЕ ЭФФЕКТЫ ФАЗОВЫХ ПЕРЕХОДОВ.

УРАВНЕНИЕ КЛАПЕЙРОНА – КЛАУЗИУСА.

Переход компонента из одной фазы в другую сопровождается выделением или поглощением теплоты, которую можно определить количественно на основе фундаментального уравнения термодинамики:

(*)

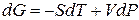
ВЫВОД И АНАЛИЗ УРАВНЕНИЯ КЛАПЕЙРОНА – КЛАУЗИУСА.

Для любого равновесного перехода вещества из одной фазы α в другую фазу β, применяя уравнение (*) к каждой из фаз, можно написать

Индексы α и β отражают принадлежность параметров к соответствующей фазе. В равновесных условиях между фазами α и β изменение энергии Гиббса отсутствует, т.е.

Приравнивая правые части уравнений 1 и 2, получим

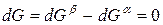
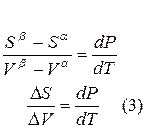
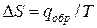
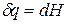
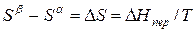
Для равновесного обратимого процесса согласно уравнениям и запишем

а уравнение (3) примет вид

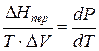
где ∆H_пер – теплота фазового перехода.

Тепловой эффект, сопровождающий фазовый переход, определяется следующим образом:

уравнение

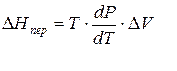
Клапейрона–Клаузиуса

где ∆V – изменение объема в результате фазового перехода; dP/dT – изменение давления в зависимости от температуры при сохранении равновесия между двумя фазами.

Уравнение Клапейрона–Клаузиуса связывает тепловой эффект процесса с изменением давления насыщенного пара, температурой и изменением объема в процессе фазового перехода.

Для процессов испарения ж→п и сублимации тв→п уравнение Клапейрона–Клаузиуса можно представить следующим образом:

где ∆H_исп , ∆H_суб – теплоты испарения и сублимации; V_п, V_ж, V_тв – мольные объемы пара, жидкости и твердого тела соответственно.

В процессе испарения и сублимации наблюдается значительное изменение удельного объема ∆V и существенное изменение величины dP/dT. При плавлении, напротив, изменение ∆V невелико, и величина dP/dT незначительна.

Пример 1. Проведем расчет по уравнению Клапейрона–Клаузиуса температуры плавления фенола Т_пл. Плотность твердого фенола ρ_тв при атмосферном давлении составляет 1,072∙10 3 кг/м 3 , а жидкого ρ_ж = 1,056∙10 3 кг/м 3 ; теплота плавления ∆H_пл = 1,045∙10 5 Дж/кг; температура замерзания 314,2 К. Определим dP/dT и температуру плавления при Р = 5,065∙10 7 Па:

Прирост температуры плавления при повышении давления на 1 атм ( 1,013∙10 5 Па) составляет 4,525∙10 -8 град/Па. При увеличении давления до 5,065∙10 7 Па температура плавления увеличивается на ∆T = (dT/dP)∆P = 4,525∙10 -8 ∙ 5,065∙10 7 = 2,29 К, т.е. составит Т_пл = 314,2+2,29 = 316,49 К.

Следует иметь в виду, что в процессе плавления у большинства веществ V_ж > V_{тв ,} тогда ∆V>0 и при повышении давления Р↑ температура плавления повышается Т↑.

Однако, такие вещества как вода (Н₂О), висмут (Bi), имеют объем твердой фазы V_тв больше, чем объем жидкой фазы V_ж уд = 10 -3 м 3 /кг и V_тв уд = 1,091·10 -3 м 3 /кг; теплота плавления ∆H_пл = 332,4 кДж/кг:

Это значение показывает, что для понижения температуры таяния льда на один градус Кельвина необходимо увеличить давление на 1,34∙10 7 Па, т.е. примерно на 134 атмосферы, что нереально, поскольку такое давление лед не выдерживает – трескается.

Таяние льда происходит в основном в результате трения и превращения работы в теплоту при скольжении конька по льду, а не за счет повышения давления на лед.

Уравнение для процесса испарения 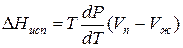можно представить в интегральном виде. Мольный объем пара значительно превосходит мольный объем жидкости, V_п >> V_{ж ,} т.е. величиной V_ж можно пренебречь. Тогда уравнение Клапейрона–Клаузиуса запишется в виде:

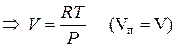
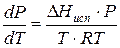
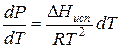
Пар подчиняется законам идеального газа: PV=RT , тогда , преобразуем уравнение, переставляя давление Р в левую часть уравнения, а dT в правую часть. Получаем:

или

Проведем интегрирование уравнения (1) в пределах от Т₁ до Т₂ и соответственно от Р₁ до Р₂ при условии, что в области невысоких давлений пара ∆Н_исп ≈ const; в результате интегрирования получим:

∆Н_исп / R = const, выносим за знак интеграла

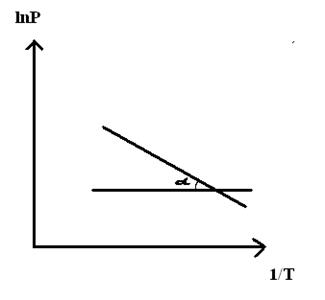
При помощи уравнения (2) можно графически определить значения теплоты испарения, если известны давления Р₁ и Р₂ и соответствующие им температуры испарения Т₁ и Т₂ . Для этого необходимо отложить на оси абсцисс значения обратной температуры, а на оси ординат – lnP.

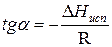
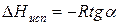
Зависимость lnP от 1/Т будет линейной, а тангенс угла наклона этой прямой равен , т.е. , а

Расчетные значения ∆Н_исп получаются с достаточной для практики точностью, не уступающей точности непосредственного измерения. Возможно использование уравнения (2) для обратного расчета, когда по значению ∆Н_исп определяют изменение давления при изменении температуры в процессе испарения.

Теплоту фазовых переходов можно определить и по величине стандартной энтальпии образования, в зависимости от фазового состояния продуктов реакции.

Пример. Лучше всего это показать на примере теплоты образования воды из газообразных кислорода и водорода, которая составляет

для водяного пара ∆Н_(г) 0 = -241,82 кДж/моль; для воды в жидком состоянии ∆Н_(ж) 0 = -285,83 кДж/моль; для льда ∆Н_(тв) 0 = -291,82 кДж/моль. Теплота конденсации воды равна:

а теплота превращения воды в лед:

Как видно, тепловой эффект фазовых переходов значительно меньше теплоты образования веществ.

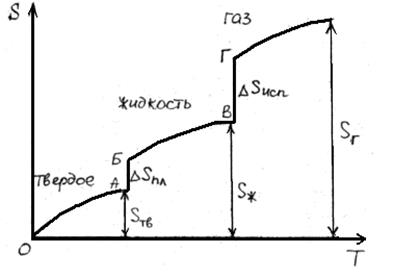
В результате фазовых переходов происходит изменение энтропии. Такие изменения в зависимости от температуры представим на рисунке.

Как известно, энтропия идеального кристалла при абсолютном нуле равна нулю. С ростом температуры атомы (ионы) флуктуировать относительно равновесного положения, число возможных способов их размещения растет, и энтропия увеличивается (ΔS>0). При достижении температуры плавления (точка А на рисунке) кристаллическая решетка разрушается скачкообразно (отрезок АБ), увеличивается термодинамическая вероятность системы W, а в соответствии с формулой S=k∙lnW (где k – постоянная Больцмана) энтропия при переходе от твердого в жидкое состояние растет. Более значительный скачок энтропии имеет место при переходе из жидкого состояния в газообразное (отрезок ВГ), когда ближний порядок расположения частиц друг относительно друга нарушается, и движение частиц становится хаотичным.

Пример. Оценим скачок энтропии на примере фазовых переходов воды:

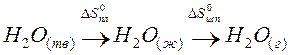
когда известны стандартные абсолютные значения энтропии S_тв 0 =39,4; S_ж 0 =69,9; S_г 0 =188,7 Дж/(моль·К).

В соответствии с рисунком для воды

По известной энтальпии фазового перехода можно рассчитать изменение энтропии в соответствии с формулой

Пример.Вычислим изменение энтропии в процессе парообразования 1 моля этилхлорида при 12,3 0 С, когда теплота испарения ∆Н_исп =24,16 кДж/моль.

Молекулярная масса 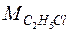= 64,5 г/моль.

В заключение отмечу, что мы рассматривали лишь фазовые переходы I рода. При фазовых переходах I рода свойства веществ, выражаемые, например, через химический потенциал, первыми производными одной из характеристических функций, изменяются скачком при непрерывном изменении соответствующих параметров: температуры, давления, объема и энтропии. При этом выделяется или поглощается теплота перехода ∆Н_пер в соответствии с уравнением Клапейрона–Клаузиуса.

Кроме них, однако, существуют фазовые переходы II рода. Они не сопровождаются выделением или поглощением теплоты, для них уравнение Клапейрона–Клаузиуса теряет смысл. Эти переходы характеризуют изменения в системе, которые не определяются объемом и запасом энергии. В этом случае первые производные одной из характеристических функций непрерывны, а вторые производные (например, теплоемкость) изменяются скачком. К фазовым переходам II рода относятся переходы парамагнетика в ферромагнетик, диэлектрика в сегнетоэлектрик, а также процессы возникновения сверхтекучести, сверхпроводимости и др.

В настоящее время насчитывается около 400 твердых минералов, для которых наблюдаются фазовые переходы II рода: рутил, анатаз, алмаз и особенно кварц, который имеет семь модификаций, причем наряду с фазовыми переходами I рода наблюдаются фазовые переходы II рода. Так, при 573 0 С и переходе модификации кварца β α теплоемкость и коэффициент линейного расширения изменяются скачкообразно (I род), но при этом поглощается теплота 10,9 кДж/моль (II род).

\|	следующая лекция ==>
ДИАГРАММА СОСТОЯНИЯ СЕРЫ.	\|	ХАРАКТЕРИСТИКА И СВОЙСТВА РАСТВОРОВ.

Дата добавления: 2016-02-02 ; просмотров: 3086 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Видео:Лекция №6 "Фазовые переходы. Газ Ван-дер-Ваальса"Скачать

Физическая химия

Главная > Документ

Информация о документе
Дата добавления:
Размер:
Доступные форматы для скачивания:

§ 3. Фазовые переходы. Уравнение Клапейрона-Клаузиуса

В системе, состоящей из нескольких фаз чистого вещества, находящихся в равновесии, возможны переходы вещества из одной фазы в другую. Такие переходы называются фазовыми переходами или превращениями агрегатных состояний.

Рассмотрим равновесный переход одного моля вещества из одной фазы (1) в другую (2), совершающийся при постоянных давлении и температуре. Энергии Гиббса ( G 1 и G 2 ) моля вещества в фазах 1 и 2 равны (условие равновесия). Следовательно:

G 2 = G 1 (III, 14)

Напишем уравнения (III, 13б) полных дифференциалов для энергии Гиббса одного моля чистого вещества в двух равновесных фазах 1 и 2:

dG 1 = V 1 dP – S 1 dT

dG 2 = V 2 dP – S 2 dT (III, 15)

Вычитая верхнее уравнение из нижнего, получим:

dG 2 – dG 1 = ( V 2 – V 1 ) dP – ( S 2 – S 1 ) dT

Изменения P и Т здесь были не независимыми, а такими, при которых сохранялось равновесие между фазами 1 и 2. Таким образом, между P и Т сохранялась функциональная связь, соответствующая фазовому равновесию. Поэтому, если G 1 = G 2 (равновесие при давлении P и температуре Т ), то G 1 + dG 1 = G 2 + dG 2 (равновесие при давлении P + dP и температуре T + dT ), т. е. dG l = dG 2 или dG 2 – dG 1 = 0. Следовательно

( V 2 – V 1 ) dP – ( S 2 – S 1 ) dT = 0

(III, 16)

Взаимное превращение, фаз рассматривалось здесь как равновесное и изотермическое, поэтому:

S 2 – S 1 =  S = = = (III, 17)

Здесь – теплота фазового превращения, поглощаемая при переходе моля вещества из фазы 1 в фазу 2; V 2 – V 1 – разность мольных объёмов двух фаз.

Из уравнений (III, 16) и (III, 17) получим:

(III, 18)

Уравнение (III, 18) называется уравнением Клапейрона — Клаузиуса и является общим термодинамическим уравнением, приложимым ко всем фазовым переходам чистых веществ, т.е. к превращениям агрегатных состояний.

При превращении одной фазы в другую такие свойства как удельный или мольный объём, внутренняя энергия и энтропия одного грамма или одного моля вещества изменяются скачкообразно. Однако отсюда не следует, что внутренняя энергия всей двухфазной системы не является в этом случае непрерывной функцией её состояния. В самом деле, система, состоявшая в начале процесса, например, из некоторого количества льда при 0°С и 1 атм, при постоянном давлении и подведении теплоты превращается в двухфазную систему лед-жидкая вода, в которой по мере поглощения теплоты масса льда постепенно и непрерывно убывает, а масса воды растет. Поэтому также постепенно и непрерывно изменяются такие свойства системы в целом как внутренняя энергия, энтальпия, энтропия и др.

§ 4. Фазовые переходы первого рода. Плавление. Испарение

Фазовые переходы, характеризующиеся равенством изобарных потенциалов двух сосуществующих в равновесии фаз и скачкообразным изменением энтропии и объема при переходе вещества из одной фазы в другую, – называются фазовыми переходами первого рода. К ним относятся агрегатные превращения – плавление, испарение, возгонка и др.

Из фазовых переходов первого рода рассмотрим плавление и испарение, представляющие более общий интерес, чем другие процессы.

Плавление. Теплота плавления – перехода твердой фазы в жидкую – всегда положительна. Объём (мольный, удельный) жидкой фазы ( V ж = V 2 ) в общем случае может быть больше или меньше объёма того же количества твердой фазы ( V т = V 1 ) . Отсюда в соответствии с уравнением (III, 18) вытекает, что величина dP / dT или обратная ей величина dT / dP , характеризующая изменение температуры с увеличением давления, может быть положительной или отрицательной. Это значит, что температура плавления может повышаться или понижаться с увеличением давления.

Так, для бензола ( t пл. = 5,4°C; = 9986 Дж / моль; V ж = 87,28 см 3 /моль; V т = 86,27 см 3 /моль ) получаем по уравнению (III, 18):

Па/К

Обратная величина dT / dP = 0,0282 К/Па. Таким образом, с ростом давления вблизи точки плавления температура плавления бензола повышается.

Величина dT / dP положительна для огромного большинства веществ. Она имеет отрицательное значение лишь для воды, висмута и немногих других веществ, для которых плотность жидкости при температуре плавления больше плотности твердой фазы и ( V ж – V т )

Испарение. Теплота испарения – перехода жидкой фазы в газообразную – так же, как и теплота плавления, положительна. В этом случае всегда объём (удельный, мольный) газа больше соответствующего объёма жидкости, т. е. в уравнении (III, 18) всегда V 2 > V 1 . Поэтому dP / dT , а значит, и dT / dP также всегда положительны. Следовательно, температура испарения всегда повышается с ростом давления.

При температурах, далеких от критической, плотность насыщенного пара во много раз меньше плотности жидкости, а обратная величина – мольный (удельный) объём пара во много раз больше мольного (удельного) объёма жидкости. Поэтому значением V 1 = V ж в уравнении (III, 18) можно пренебречь, и оно примет вид:

(III, 18a)

Если вдали от критической температуры насыщенный пар можно считать идеальным газом, тогда = RT / P , и из уравнения (III, 18) получим 1 :

(III, 19)

(III, 19а)

Теплота испарения жидкостей изменяется с температурой, не сильно убывая при средних температурах и очень сильно вблизи критической температуры, при которой = 0. Например, для Н 2 О:

, кал/г

Таблица 1. Энтальпия и энтропия испарения некоторых жидкостей при нормальной температуре кипения ( Р = 1 атм)

,
кал/моль

,
кал/моль· K

§ 5. Зависимость давления насыщенного пара от температуры

Давление насыщенного пара жидкости резко увеличивается с повышением температуры. Это видно из рис.2, на котором изображены кривые давления пара некоторых жидкостей, начинающиеся в точках плавления и оканчивающиеся в критических точках.

Рис. 2. Зависимость давления насыщенного пара некоторых жидкостей от температуры.

Функциональная зависимость давления насыщенного пара жидкости от температуры может быть выражена уравнением (III, 18), а вдали от критической температуры уравнением (III, 19).

Считая теплоту испарения (возгонки) постоянной в небольшом интервале температур, можно проинтегрировать уравнение (III, 19а)

(III, 20)

Представив уравнение (III, 20) в виде неопределенного интеграла, получим:

(III, 21),

где С – константа интегрирования.

В соответствии с этими уравнениями зависимость давления насыщенного пара жидкости (или кристаллического вещества) от температуры может быть выражена прямой линией в координатах (в этом случае тангенс наклона прямой равен ). Такая зависимость имеет место лишь в некотором интервале температур, далеких от критической.

На рис.3 изображена зависимость давления насыщенного пара некоторых жидкостей в указанных координатах, удовлетворительно укладывающаяся на прямые линии в интервале 0-100°С.

Однако уравнение (III, 21) не охватывает зависимости давления насыщенного пара от температуры во всем интервале температур – от температуры плавления до критической. С одной стороны, теплота испарения зависит от температуры, и интегрирование должно производиться с учётом этой зависимости. С другой стороны, насыщенный пар при высоких температурах нельзя считать идеальным газом. Поэтому уравнение, охватывающее зависимость P = f ( T ) в широком интервале температур, неизбежно становится эмпирическим.

Рис.3. Зависимость логарифма давления насыщенного пара некоторых жидкостей от обратной температуры.

§ 6. Сверхкритическое состояние вещества.

Сверхкритическое состояние – четвертая форма агрегатного состояния, в которое способны переходить многие органические и неорганические вещества.

Впервые сверхкритическое состояние вещества обнаружил Каньяр де ла Тур в 1822 году. Настоящий интерес к новому явлению возник 1869 году после экспериментов Т.Эндрюса. Проводя опыты в толстостенных стеклянных трубках, учёный исследовал свойства CO 2 , легко сжижающегося при повышении давления. В результате он установил, что при 31° С и 7,2 МПа , мениск – граница, разделяющая жидкость и находящийся в равновесии с ней пар, исчезает, при этом система становится гомогенной (однородной) и весь объем приобретает вид молочно-белой опалесцирующей жидкости. При дальнейшем повышении температуры она быстро становится прозрачной и подвижной, состоящей из постоянно перетекающих струй, напоминающих потоки теплого воздуха над нагретой поверхностью. Дальнейшее повышение температуры и давления не приводило к видимым изменениям.

Точку, в которой происходит такой переход, он назвал критической, а состояние вещества, находящегося выше этой точки – сверхкритическим. Несмотря на то, что внешне это состояние напоминает жидкость, в применении к нему сейчас используется специальный термин – сверхкритический флюид (от английского слова fluid , то есть «способный течь»). В современной литературе принято сокращенное обозначение сверхкритических флюидов – СКФ.

Расположение линий, разграничивающих области газообразного, жидкого и твердого состояний, а также положение тройной точки, где сходятся все три области, для каждого вещества индивидуальны. Сверхкритическая область начинается в критической точке (обозначена звездочкой), которая характеризуется непременно двумя параметрами – температурой ( Т кр . ) и давлением ( Р кр . ). Понижение либо температуры, либо давления ниже критических значений выводит вещество из сверхкритического состояния.

Факт существования критической точки позволил понять, почему некоторые газы, например, водород, азот и кислород долгое время не удавалось получить в жидком виде при повышении давления, из-за чего их называли перманентными газами (от латинского permanentis – «постоянный»). На приведённой выше диаграмме видно, что область существования жидкой фазы расположена слева от линии критической температуры. Таким образом, для сжижения какого-либо газа его необходимо сначала охладить до температуры ниже критической. У СО 2 критическая температура выше комнатной, поэтому его можно сжижать при указанных условиях, повышая давление. У азота критическая температура намного ниже: –146,95° С, поэтому, если сжимать азот, находящийся при нормальных условиях, можно достичь в конечном итоге сверхкритической области, но жидкий азот при этом образоваться не может. Необходимо сначала охладить азот ниже критической температуры и затем, повышая давление, достичь области, где возможно существование жидкости. Аналогичная ситуация для водорода, кислорода, поэтому перед сжижением их охлаждают до температуры ниже критической, и лишь затем повышают давление. Сверхкритическое состояние возможно для большинства веществ, нужно лишь, чтобы вещество не разлагалось при критической температуре. В сравнении с указанными веществами критическая точка воды достигается с большим трудом: t кр = 374,2° С и Р кр = 21,4 МПа .

Критическая точка признается как важный физический параметр вещества, такой же, как температуры плавления или кипения. Плотность СКФ исключительно низкая, например, вода в состоянии СКФ имеет плотность в три раза ниже, чем при обычных условиях. Все СКФ имеют крайне низкую вязкость.

Сверхкритические флюиды представляют собой нечто среднее между жидкостью и газом. Они могут сжиматься как газы (обычные жидкости практически несжимаемы) и, в тоже время, способны растворять многие вещества в твёрдом и жидком состояниях, что газам несвойственно. Сверхкритический этанол (при температуре выше 234° С) очень легко растворяет некоторые неорганические соли ( CoCl 2 , KBr , KI ). Диоксид углерода, закись азота, этилен и некоторые другие газы в состоянии СКФ приобретают способность растворять многие органические вещества – стеариновую кислоту, парафин, нафталин. Свойства сверхкритического СО 2 как растворителя можно регулировать – при повышении давления его растворяющая способность резко увеличивается.

Сверхкритические флюиды стали широко использовать только в 1980-х, когда общий уровень развития промышленности сделал установки для получения СКФ широко доступными. С этого момента началось интенсивное развитие сверхкритических технологий. СКФ – это не только хорошие растворители, но и вещества с высоким коэффициентом диффузии, т.е. они легко проникают в глубинные слои различных твердых веществ и материалов. Наиболее широкое применение нашёл сверхкритический СО 2 , который оказался растворителем широкого круга органических соединений. Диоксид углерода стал лидером в мире сверхкритических технологий, т.к. обладает целым комплексом преимуществ. Перевести его в сверхкритическое состояние достаточно легко ( t кр – 31° С, Р кр – 73,8 атм. ), кроме того, он не токсичен, не горюч, не взрывоопасен, к тому же, дешев и доступен. С точки зрения любого технолога он является идеальным компонентом любого процесса. Особую привлекательность ему придает то, что он является составной частью атмосферного воздуха и, следовательно, не загрязняет окружающую среду. Сверхкритический СО 2 можно считать экологически абсолютно чистым растворителем. Приведём только некоторые примеры его использования.

Кофеин – препарат, используемый для улучшения деятельности сердечно-сосудистой системы, получают из кофейных зерен даже без их предварительного измельчения. Полнота извлечения достигается за счет высокой проникающей способности СКФ. Зерна помещают в автоклав – ёмкость, выдерживающую повышенное давление, затем подают в неё газообразный СО 2 , далее создают необходимое давление (>73 атм. ), в результате СО 2 переходит в сверхкритическое состояние. Всё содержимое перемешивают, после чего флюид вместе с растворенным кофеином сливают в открытую емкость. Диоксид углерода, оказавшись в условиях атмосферного давления, превращается в газ и улетает в атмосферу, а экстрагированный кофеин остается в открытой емкости в чистом виде.

Применение СКФ оказалось весьма успешным для очистки от загрязнений электронных схем в процессе их производства, так как на них не остается никаких следов очищающего растворителя.

В связи с быстрыми темпами выработки активной части запасов легкой нефти резко возрос интерес к методам увеличения нефтеотдачи пластов. Если в 70–80 годы XX века число проектов, направленных на решение проблемы увеличения нефтеотдачи посредством нагнетания смешивающихся углеводородных растворителей, «инертных» газов и диоксида углерода было сопоставимо, то в конце XX и начале XXI столетий только метод нагнетания СО 2 имел устойчивую тенденцию роста. Эффективность применения СО 2 для повышения нефтеотдачи доказана не только экспериментальными и теоретическими работами, но и результатами многочисленных промышленных испытаний.

Не стоит забывать, что технология увеличения нефтеотдачи пластов с использованием СО 2 позволяет параллельно решать проблему консервации огромного количества выделяемого промышленностью углекислого газа.

Особенности процесса воздействия нагнетаемого CO 2 на нефтегазовую залежь зависят от его агрегатного состояния.

Превышение давления и температуры выше критических значений для углекислого газа (а это наиболее вероятная ситуация в пластовых условиях), предопределяет его сверхкритическое состояние. В этом случае CO 2 , обладающий исключительной растворяющей способностью по отношению к углеводородным жидкостям при прямом растворении в пластовой нефти, снижает её вязкость и резко улучшает фильтрационные свойства. Указанное обстоятельство даёт все основания отнести СКФ – технологии повышения нефтеотдачи пластов к одним из наиболее перспективных.

Видео:Теплофизика Л7. Фазовые переходы. Уравнение Клапейрона - Клаузиуса. Уравнение Ван-дер-ВаальсаСкачать

КЛАПЕЙРО́НА – КЛА́УЗИУСА УРАВНЕ́НИЕ

В книжной версии

Том 14. Москва, 2009, стр. 215

Скопировать библиографическую ссылку:

КЛАПЕЙРО́ НА – КЛ А́УЗИУСА УРАВНЕ́ НИЕ, уравнение, характеризующее фазовые переходы 1-го рода (плавление, испарение, сублимацию, полиморфные превращения); устанавливает связь между равновесными значениями абсолютной темп-ры $T$ и давления $p $ при фазовых переходах 1-го рода однокомпонентной системы с теплотой фазового перехода и изменением фазового объёма. К. – К. у. имеет вид: $$frac

=frac <L_>,$$ где $L_$ – удельная теплота фазового перехода $1→2, V_1$ и $V_2 $ – удельные объёмы фаз $1$ и $2$ . Производная $dp/dT$ определяет угол наклона касательной в каждой точке кривой равновесия двух фаз на фазовой диаграмме $p – T$ .