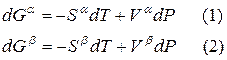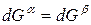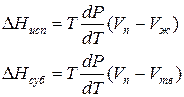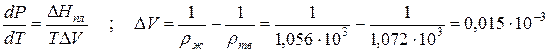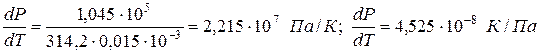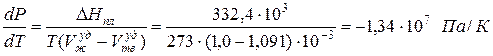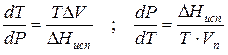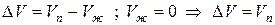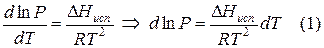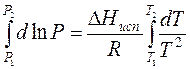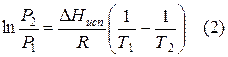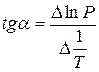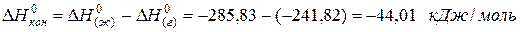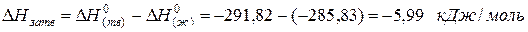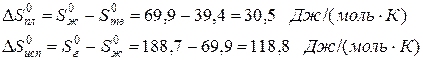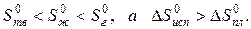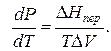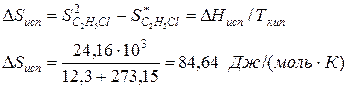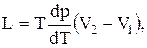ТЕПЛОВЫЕ ЭФФЕКТЫ ФАЗОВЫХ ПЕРЕХОДОВ.
УРАВНЕНИЕ КЛАПЕЙРОНА – КЛАУЗИУСА.
Переход компонента из одной фазы в другую сопровождается выделением или поглощением теплоты, которую можно определить количественно на основе фундаментального уравнения термодинамики:
(*)
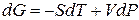
ВЫВОД И АНАЛИЗ УРАВНЕНИЯ КЛАПЕЙРОНА – КЛАУЗИУСА.
Для любого равновесного перехода вещества из одной фазы α в другую фазу β, применяя уравнение (*) к каждой из фаз, можно написать
Индексы α и β отражают принадлежность параметров к соответствующей фазе. В равновесных условиях между фазами α и β изменение энергии Гиббса отсутствует, т.е.
, 
Приравнивая правые части уравнений 1 и 2, получим
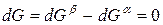
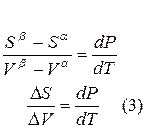
Для равновесного обратимого процесса согласно уравнениям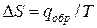 
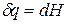
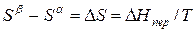
и 
запишем
,
а уравнение (3) примет вид
,
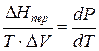
где ∆Hпер – теплота фазового перехода.
Тепловой эффект, сопровождающий фазовый переход, определяется следующим образом:
уравнение
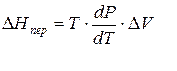
Клапейрона–Клаузиуса
где ∆V – изменение объема в результате фазового перехода; dP/dT – изменение давления в зависимости от температуры при сохранении равновесия между двумя фазами.
Уравнение Клапейрона–Клаузиуса связывает тепловой эффект процесса с изменением давления насыщенного пара, температурой и изменением объема в процессе фазового перехода.
Для процессов испарения ж→п и сублимации тв→п уравнение Клапейрона–Клаузиуса можно представить следующим образом:
где ∆Hисп , ∆Hсуб – теплоты испарения и сублимации; Vп, Vж, Vтв – мольные объемы пара, жидкости и твердого тела соответственно.
В процессе испарения и сублимации наблюдается значительное изменение удельного объема ∆V и существенное изменение величины dP/dT. При плавлении, напротив, изменение ∆V невелико, и величина dP/dT незначительна.
Пример 1. Проведем расчет по уравнению Клапейрона–Клаузиуса температуры плавления фенола Тпл. Плотность твердого фенола ρтв при атмосферном давлении составляет 1,072∙10 3 кг/м 3 , а жидкого ρж = 1,056∙10 3 кг/м 3 ; теплота плавления ∆Hпл = 1,045∙10 5 Дж/кг; температура замерзания 314,2 К. Определим dP/dT и температуру плавления при Р = 5,065∙10 7 Па:
Прирост температуры плавления при повышении давления на 1 атм ( 1,013∙10 5 Па) составляет 4,525∙10 -8 град/Па. При увеличении давления до 5,065∙10 7 Па температура плавления увеличивается на ∆T = (dT/dP)∆P = 4,525∙10 -8 ∙ 5,065∙10 7 = 2,29 К, т.е. составит Тпл = 314,2+2,29 = 316,49 К.
Следует иметь в виду, что в процессе плавления у большинства веществ Vж > Vтв , тогда ∆V>0 и при повышении давления Р↑ температура плавления повышается Т↑.
Однако, такие вещества как вода (Н2О), висмут (Bi), имеют объем твердой фазы Vтв больше, чем объем жидкой фазы Vж уд = 10 -3 м 3 /кг и Vтв уд = 1,091·10 -3 м 3 /кг; теплота плавления ∆Hпл = 332,4 кДж/кг:
Это значение показывает, что для понижения температуры таяния льда на один градус Кельвина необходимо увеличить давление на 1,34∙10 7 Па, т.е. примерно на 134 атмосферы, что нереально, поскольку такое давление лед не выдерживает – трескается.
Таяние льда происходит в основном в результате трения и превращения работы в теплоту при скольжении конька по льду, а не за счет повышения давления на лед.
Уравнение для процесса испарения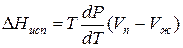 
можно представить в интегральном виде. Мольный объем пара значительно превосходит мольный объем жидкости, Vп >> Vж , т.е. величиной Vж можно пренебречь. Тогда уравнение Клапейрона–Клаузиуса запишется в виде:
Пар подчиняется законам идеального газа: PV=RT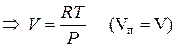 
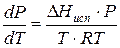
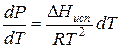
, тогда 
, преобразуем уравнение, переставляя давление Р в левую часть уравнения, а dT в правую часть. Получаем:
или
Проведем интегрирование уравнения (1) в пределах от Т1 до Т2 и соответственно от Р1 до Р2 при условии, что в области невысоких давлений пара ∆Нисп ≈ const; в результате интегрирования получим:
∆Нисп / R = const, выносим за знак интеграла
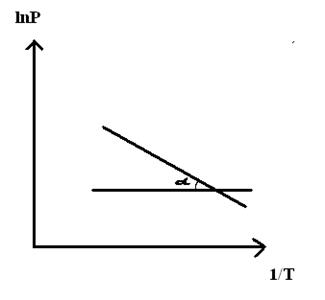
При помощи уравнения (2) можно графически определить значения теплоты испарения, если известны давления Р1 и Р2 и соответствующие им температуры испарения Т1 и Т2 . Для этого необходимо отложить на оси абсцисс значения обратной температуры, а на оси ординат – lnP.
Зависимость lnP от 1/Т будет линейной, а тангенс угла наклона этой прямой равен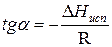 
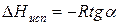
, т.е. 
, а 
Расчетные значения ∆Нисп получаются с достаточной для практики точностью, не уступающей точности непосредственного измерения. Возможно использование уравнения (2) для обратного расчета, когда по значению ∆Нисп определяют изменение давления при изменении температуры в процессе испарения.
Теплоту фазовых переходов можно определить и по величине стандартной энтальпии образования, в зависимости от фазового состояния продуктов реакции.
Пример. Лучше всего это показать на примере теплоты образования воды из газообразных кислорода и водорода, которая составляет
для водяного пара ∆Н(г) 0 = -241,82 кДж/моль; для воды в жидком состоянии ∆Н(ж) 0 = -285,83 кДж/моль; для льда ∆Н(тв) 0 = -291,82 кДж/моль. Теплота конденсации воды равна:
а теплота превращения воды в лед:
Как видно, тепловой эффект фазовых переходов значительно меньше теплоты образования веществ.
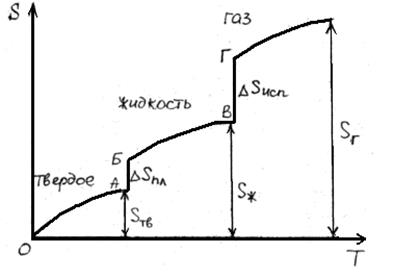
В результате фазовых переходов происходит изменение энтропии. Такие изменения в зависимости от температуры представим на рисунке.
Как известно, энтропия идеального кристалла при абсолютном нуле равна нулю. С ростом температуры атомы (ионы) флуктуировать относительно равновесного положения, число возможных способов их размещения растет, и энтропия увеличивается (ΔS>0). При достижении температуры плавления (точка А на рисунке) кристаллическая решетка разрушается скачкообразно (отрезок АБ), увеличивается термодинамическая вероятность системы W, а в соответствии с формулой S=k∙lnW (где k – постоянная Больцмана) энтропия при переходе от твердого в жидкое состояние растет. Более значительный скачок энтропии имеет место при переходе из жидкого состояния в газообразное (отрезок ВГ), когда ближний порядок расположения частиц друг относительно друга нарушается, и движение частиц становится хаотичным.
Пример. Оценим скачок энтропии на примере фазовых переходов воды:
,
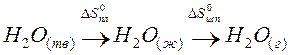
когда известны стандартные абсолютные значения энтропии Sтв 0 =39,4; Sж 0 =69,9; Sг 0 =188,7 Дж/(моль·К).
В соответствии с рисунком для воды 
По известной энтальпии фазового перехода можно рассчитать изменение энтропии в соответствии с формулой 
Пример.Вычислим изменение энтропии в процессе парообразования 1 моля этилхлорида при 12,3 0 С, когда теплота испарения ∆Нисп =24,16 кДж/моль.
Молекулярная масса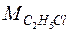 
= 64,5 г/моль.
В заключение отмечу, что мы рассматривали лишь фазовые переходы I рода. При фазовых переходах I рода свойства веществ, выражаемые, например, через химический потенциал, первыми производными одной из характеристических функций, изменяются скачком при непрерывном изменении соответствующих параметров: температуры, давления, объема и энтропии. При этом выделяется или поглощается теплота перехода ∆Нпер в соответствии с уравнением Клапейрона–Клаузиуса.
Кроме них, однако, существуют фазовые переходы II рода. Они не сопровождаются выделением или поглощением теплоты, для них уравнение Клапейрона–Клаузиуса теряет смысл. Эти переходы характеризуют изменения в системе, которые не определяются объемом и запасом энергии. В этом случае первые производные одной из характеристических функций непрерывны, а вторые производные (например, теплоемкость) изменяются скачком. К фазовым переходам II рода относятся переходы парамагнетика в ферромагнетик, диэлектрика в сегнетоэлектрик, а также процессы возникновения сверхтекучести, сверхпроводимости и др.
В настоящее время насчитывается около 400 твердых минералов, для которых наблюдаются фазовые переходы II рода: рутил, анатаз, алмаз и особенно кварц, который имеет семь модификаций, причем наряду с фазовыми переходами I рода наблюдаются фазовые переходы II рода. Так, при 573 0 С и переходе модификации кварца β 
α теплоемкость и коэффициент линейного расширения изменяются скачкообразно (I род), но при этом поглощается теплота 10,9 кДж/моль (II род).
| | | следующая лекция ==> | |
| ДИАГРАММА СОСТОЯНИЯ СЕРЫ. | | | ХАРАКТЕРИСТИКА И СВОЙСТВА РАСТВОРОВ. |
Дата добавления: 2016-02-02 ; просмотров: 3224 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Видео:Фазовые диаграммы. Тройная точка. Критическое состояние вещества. 10 класс.Скачать
Фазовые равновесия и фазовые переходы. Уравнение Клапейрона-Клаузиуса
Сначала рассмотрим условия равновесия изолированной двухфазной однокомпонентной системы вода-пар, на которую действует только всестороннее давление. Общее условие равновесия этой системы есть:
где г|’ и Г|» — энтропии соответственно воды и пара. С помощью уравнения (2.38) перепишем соотношение (6.9) в виде:
Учитывая, что экстенсивные параметры системы подчинены следующим уравнениям связей:
предыдущее выражение можно записать в виде:
Из этого уравнения находятся следующие частные условия фазового равновесия однокомпонентной системы:
Если T=const и p=const, то эти три условия можно записать в виде одного равенства химических потенциалов вещества в фазах:
При равенстве же двух фаз разных веществ должны выполняться условия
где верхний индекс означает фазу, а нижний — компонент, т. е. равенство температур и давлений в фазах. На химические потенциалы никаких условий в этом случае не накладывается, так как обмена частицами между такими фазами быть не может.
Из формул (6.10) и (6.12) можно сделать общий вывод, что при равновесии гетерогенной системы из п фаз с к компонентами температура, давление и химические потенциалы каждого компонента во всех фазах одинаковы.
Это позволяет определить количество фаз (состоящих из нескольких компонентов), способных одновременно находится в равновесии (число независимых переменных гетерогенной системы), которые можно изменять, не нарушая ее равновесия. Эта задача была решена Дж. Гиббсом, который установил, что в системе из к компонент одновременно в равновесии может находиться не больше, чем к+2 Лазы:
Выражение (6.13) называется правилом фаз Гиббса. Это правило получено для гетерогенной системы, на которую действует только одна сила давления. Соотношение (6.13) можно записать в виде:
где / — число термодинамических степеней свободы системы (число независимых переменных, которые могут быть произвольно изменены без нарушения равновесия гетерогенной системы).
При равновесии двух фаз (я=2) системы с одним компонентом (Л=1) число степеней свободы f=. Этот вывод можно получить и из равенства (6.11), которое связывает температуру и давление в фазах. Одну из них можно взять за независимую переменную, тогда получим зависимость давления от температуры при равновесии: 
На Тр-плоскости это будет соответствовать кривой равновесия фаз. При этом точки, лежащие по обеим сторонам этой кривой, представляют собой различные однородные состояния тела.
При равновесии трех фаз одного и того же вещества, например лед-вода-пар, число степеней свободы j= 0, т. е. равновесие в этом случае достигается только в одной точке на 7р-плоскости (рис. 6.1). Температуру и давление в этой точке можно получить из следующих уравнений: 
Состояние, определяемое этими значениями переменных Т и р, называется тройной точкой. Тройная точка для пресной воды имеет следующие значения: 7H),0100 o С при р=509 Па. Для морской воды температура тройной точки выше температуры замерзания примерно на такую же величину.
При равновесном переходе вещества из одной фазы в другую, как и при фазовом равновесии, температура, давление и химический потенциал вещества в фазах одинаковы. В то же время имеются такие термические и калорические величины, которые при одних фазовых переходах терпят разрыв, при других — непрерывны. Поэтому различают прерывные и непрерывные фазовые переходы. Прерывные превращения называются фазовыми переходами первого рода. При этих переходах скачком изменяется удельный объем (плотность) вещества (см. например рис. 1.4) и поглощается (или выделяется) теплота. К фазовым переходам первого рода относятся плавление, кристаллизация, кипение и т. д.
Рис. 6.1. Диаграмма фазовых состояний. Сплошные линии — пресная вода, пунктирные — морская вода с соленостью 35 епс
Непрерывные фазовые переходы называются фазовыми переходами второго рода. При этих переходах скачком изменяются теплоемкость при постоянном давлении, сжимаемость, коэффициент теплового расширения и т. д.
Найдем уравнение, характеризующее фазовые переходы первого рода. Для этого воспользуемся условием равенства химических потенциалов при равновесии двух фаз (6.11). Дифференцируя (6.11), получим:
Производные, входящие в это выражение найдем, используя уравнения Гиббса-Дюгема (2.48) для одной частицы, которое выглядит таким образом:
где г) и V — энтропия и объем одной частицы. Уравнение (6.15) является дифференциальным уравнением кривой равновесия и называется уравнением Клапейрона-Клаузиуса. При изобарических процессах уравнение (6.15) можно выразить через разность энтальпий, если воспользоваться выражением (2.33):
Чаще уравнение (6.15) записывают в виде:
где Х = 7’ (г)»-г|’) — скрытая теплота перехода (теплота испарения, сублимации, плавления) на грамм (моль) вещества. При изобарических процессах — Х = Н» — Н’. Отсюда видно, что при переходе вещества, например, воды из фазового состояния с большей энтальпией в фазовое состояние с меньшей происходит отдача излишков энтальпии, а при обратном переходе необходимое количество энтальпии поступает из-за пределов термодинамической системы. Величина А. называется «скрытой» теплотой потому, что при переходе, например, жидкости в пар это тепло от жидкости «отнимается», но не происходит одновременного непосредственного нагрева окружающей воздушной среды. Нагрев может происходить только при обратном фазовом переходе — конденсации водяного пара, и этот процесс может происходить в другое время и в другом месте.
Как видно из (6.16), уравнение Клапейрона-Клаузиуса связывает между собой теплоту перехода, изменение (скачок) объема и наклон кривой равновесия в точке перехода. Основное применение уравнения (6.16) состоит в вычислении удельных теплот испарения, плавления, сублимации.
Уравнение Клапейрона-Клаузиуса вида
используется для вычисления изменения температуры фазового перехода (например, температуры замерзания).
Ранее условия равновесия описывались нами без учета поверхностных явлений. Теперь включим в рассмотрение эти процессы.
Видео:Коробов М. В. - Физическая химия. Часть 1 - Фазовые диаграммы. Фазовые переходыСкачать
Фазовые переходы I и II рода. Диаграммы состояния. Уравнение Клапейрона — Клаузиуса
Фаза вещества — это физически и химически однородная часть неоднородной системы, отделенная от других частей поверхностью раздела.
Причем различные агрегатные состояния одного и того же вещества — его разные фазы (но понятие “фаза” — шире, чем понятие “агрегатное состояние”).
В пределах одного агрегатного состояния вещество может находиться в разных фазах.
В системе может быть одновременно несколько агрегатных состояний и, следовательно, несколько фаз.
Пример: лед, вода, пар — 3 фазы.
Переход вещества из одной фазы в другую называется фазовым переходом.
Пример: лед 
вода пар.
Основное свойство фазового перехода: он всегда связан с качественными изменениями свойств вещества.
— переходы, связанные с изменением агрегатного состояния вещества;
— переходы, связанные с изменениями состава, строения и свойств вещества;
— переход кристаллического вещества из одной модификации в другую.
Различают фазовые переходы двух родов.
Фазовый переход I рода— сопровождается поглощением или выделением определенного количества тепла, которое называется теплотой фазового перехода.
Пример : плавление, кристаллизация.
Эти переходы характеризуются изменением энтропии S и объема V, но постоянством температуры Т.
Фазовый переход II рода –это процесс, не связанный с поглощением или выделением теплоты и изменением объема.
Фазовые переходы II рода характеризуются: постоянством объема и энтропии. При этих переходах скачком меняется теплоемкость.
Общая трактовка фазового перехода II рода дана Ландау.
Фазовые переходы II рода связаны с изменением симметрии. Выше точки перехода система, как правило, обладает более высокой симметрией.
Примеры: 1)с достижением приблизительно t=700 0 C железо (Fe) переходит из ферромагнитной фазы в парамагнитную.
2) при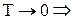 
металл становится сверхпроводником.
3) He — I при Т = 2,9 К переходит в He — II и становится сверхтекучим.
Если система однокомпонентна, т.е. состоит из химически однородного вещества, то понятие фазы совпадает с понятием агрегатного состояния. В зависимости от соотношения между средней кинетической энергией и средней потенциальной энергией оно может находиться в одном из трех агрегатных состояний: твердом, жидком, газообразном. Это определяется внешними условиями Т и р => фазовые превращения также определяются Т и р.
Для геометрического изображения фазовых превращений используют диаграмму состояний, на которой в координатах р и Т (рис.7.10) задается зависимость между температурой фазового перехода и давлением в виде кривых:
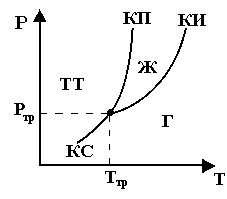
делящих поле на три части, соответствующие условиям существования :
газообразной Г фаз.
Кривые называются кривыми фазового равновесия: любая точка на них – равновесие двух фаз.
Точка, в которой пересекаются три кривые КП, КИ, КС и которая определяет условия сосуществования трех фаз, называется тройной точкой.
Любое вещество имеет только одну тройную точку.
Пример: Вода: Ттр = 273,16 К.
Термодинамика дает метод расчета кривой равновесия двух фаз одного и того же вещества.
Уравнение Клапейрона -Клаузиуса — термодинамическое уравнение, описывающее процесс перехода вещества из одной фазы в другую. Согласно этому уравнению теплота фазового перехода L ( например, теплота испарения или теплота плавления) при равновесно протекающем процессе равна :
где Т — температура перехода (процесс изотермический) — при переходе из одной фазы в другую,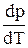 
изменение давления с температурой по кривой фазового равновесия , V2 — V1 — изменение объема при переходе из фазы в фазу.
💥 Видео
Лекция №5 "Фазовые переходы" (Попов П.В.)Скачать
Физика 10 класс: Уравнение Клапейрона-МенделееваСкачать
Физическая химия # 2. Вывод уравнения Клаузиуса-КлапейронаСкачать
8.9 Типы фазовых переходовСкачать
Физика 10 класс. Агрегатные (фазовые) переходы.Скачать
Грибов В. А. - Термодинамика и статистическая физика - Фазовые переходыСкачать
Лекция 14 Эпизод 2 Фазовые переходы первого и второго родаСкачать
Лекция №6 "Фазовые переходы. Газ Ван-дер-Ваальса"Скачать
Агрегатные состояния, фазовые переходы 8 класс, физикаСкачать
Фазовые переходы 1-го и 2-го рода. Группа ИС 19-3, студент Буераков НикитаСкачать
Теплофизика Л7. Фазовые переходы. Уравнение Клапейрона - Клаузиуса. Уравнение Ван-дер-ВаальсаСкачать
Уравнение КЛАПЕЙРОНА-КЛАЗИУСА | МОЛЕКУЛЯРКА (лекция) - КАРАВАЕВ В. А. ФизФак МГУСкачать
Фазовые переходы IIого родаСкачать
Физика. МКТ: Уравнение Менделеева-Клапейрона для идеального газа. Центр онлайн-обучения «Фоксфорд»Скачать
Грибов В.А. - Термодинамика и статистическая физика I - Фазовые переходы 2-го родаСкачать
Уравнение Ван дер Ваальса. Часть 3. Внутренняя энергия реального газа. Фазовые переходы 1 рода.Скачать
ФАЗОВЫЕ переходы II рода. Газ ВАН-ДЕР-ВААЛЬСА | МОЛЕКУЛЯРКА (лекция) - КАРАВАЕВ В. А. ФизФак МГУСкачать
Бушина Т. А. - Молекулярная физика - Фазовые переходыСкачать
