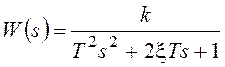Фазовое пространство в дифференциальных уравнениях (8 видео)

Фазовое пространство в дифференциальных уравнениях

При изучении закона движения материальной точки с массой удобно пользоваться векторной формой записи уравнений. Итак, пусть — закон движения материальной точки в пространстве , где — время. Это значит, что в момент времени точка имеет радиус-вектор , или, что все равно, координаты . Если точка массы движется под действием заданной силы (вектора) , то по закону Ньютона и механическому смыслу второй производной функция должна удовлетворять уравнению движения

. (1)

Векторное уравнение (1) эквивалентно системе трех скалярных уравнений

(2)

где ,, — проекции вектора на оси координат ,,.

Если считать неизвестными не только координаты точки ,,, но и проекции скорости

то мы получим систему из шести уравнений первого порядка

(3)

Векторное уравнение (1) можно также записать в виде системы двух векторных уравнений, если скорость считать неизвестной векторной функцией:

, (1’)

где — вектор с проекциями ,,.

Если ввести в рассмотрение вектор

то уравнение (1) или система (3) эквивалентны одному векторному уравнению первого порядка

(4)

в шестимерном пространстве, причем вектор

Шестимерное пространство точек

в физике называют фазовым, а кривую в шестимерном пространстве, являющуюся решением (4), называют фазовой траекторией.

Фазовое пространство – это пространство состояний движения точки по кривой.

Первые три координаты характеризуют положение точки в трехмерном пространстве , а остальные три координаты характеризуют ее скорость .

Приведенная терминология дает так называемую кинетическую интерпретацию системы уравнений.

Систему (3), или, что то же самое, (4) называют динамической системой.

Для выделения одной траектории необходимо задать начальные условия:, т.е. начальное положение точки и ее начальную скорость. Другими словами, интегральная кривая должна проходить через точку шестимерного пространства.

Таким образом, физические задачи приводят нас к необходимости рассмотрения систем дифференциальных уравнений.

Рассмотрим произвольную систему дифференциальных уравнений первого порядка вида

, (5)

где — искомые функции, а — известные функции, заданные на некотором множестве точек — мерного пространства.

Нас будут интересовать решения системы (5), удовлетворяющие начальным условиям

, (6)

где — заданная точка — мерного пространства.

Систему (5) (решенную относительно производных искомых функций!) называют нормальной (см. § 1.12, 1.13).

Если функции не зависят явно от независимого переменного , то система называется автономной нормальной системой

. (7)

Если ввести векторы в мерном пространстве

то систему (5) можно записать в виде

, (5’)

а начальные условия (6)- в форме

. (6’)

Автономную систему можно записать так:

. (7’)

Автономную систему можно интерпретировать следующим образом. В каждой точке некоторого множества n-мерного пространства определен вектор

Этим определено на указанном множестве поле векторов.

Решение описывает определенную траекторию движения точки в n-мерном пространстве, причем вектор скоростив момент ее прохождения через , совпадает с вектором.

Пространство размеренности n точек, в котором интерпретируются решения автономной системы (7’) в виде траекторий, называется фазовым пространством системы.

Траектории называются фазовыми траекториями, векторы — фазовыми скоростями.

Вопрос существования решения нормальной системы был рассмотрен в § 1.12.

Копирование информации со страницы разрешается только с указанием ссылки на данный сайт

Содержание

Фазовое пространство в дифференциальных уравнениях
Понятие о фазовом пространстве. Метод фазовой плоскости
Страницы работы
Содержание работы
🔍 Видео

Видео:Размышляю над Хаосом и Равновесием - ДиффурыСкачать

Фазовое пространство в дифференциальных уравнениях

Система обыкновенных дифференциальных уравнений называется автономной, если независимая переменная не входит явно в систему.
В теории автономных систем принято обозначать независимую переменную буквой t, а искомое решение — .
Ограничимся случаем n = 2 и в дальнейшем рассматриваем автономные системы второго порядка:

Будем полагать, что правые части системы f₁(x₁, x₂ ) , f₂(x₁, x₂) непрерывно дифференцируемы в области , т.е. справедлива теорема существования и единственности. Название автономная система оправдано тем, что решение само управляет своим изменением, поскольку производные dx₁/dt и dx₂/dt зависят только от x₁ и x₂. Автономные системы называют также динамическими системами.

Пусть x₁=j₁(t), x₂= j₂(t) — решение автономной системы второго порядка. Тогда уравнения

задают в параметрической форме кривую на плоскости. Эта кривая называется фазовой кривой или фазовой траекторией системы. Плоскость, на которой расположены фазовые траектории называется фазовой плоскостью автономной системы. Для n >2 фазовые траектории располагаются в фазовом пространстве.

Если на рисунке изображено несколько фазовых кривых системы, характеризующих качественное поведение решений системы (кривые с одинаковыми асимптотами, предельными точками и пр.), то такое изображение называется фазовым портретом системы.

Интегральные кривые рассматриваемой системы изображаются в трехмерном пространстве переменных (t, x₁, x₂) и, если x₁= f ₁(t), x₂= f ₂(t) — решение системы, то интегральная кривая задается в параметрической форме уравнениями

а фазовая траектория — не что иное, как проекция интегральной кривой на фазовую плоскость (плоскость (x₁, x₂).

ПРИМЕР 1. Фазовые кривые автономной системы.

Для фазовых кривых (фазовых траекторий) автономной системы с непрерывно дифференцируемой правой частью
, ,
справедливы следующие утверждения:

Если существует такая точка , что , то , является решением автономной системы, т.е. соответствующая фазовая траектория — точка.
Если точка (x₁(t), x₂(t)) принадлежит некоторой фазовой кривой, то при любой постоянной С точка (x₁(t+С), x₂(t+С)) принадлежит той же фазовой кривой.
Две фазовые кривые либо не имеют общих точек, либо совпадают.
Фазовая траектория, отличная от точки, есть гладкая кривая (в каждой ее точке есть ненулевой касательный вектор).
Всякая фазовая кривая принадлежит к одному из трех типов— гладкая кривая без самопересечений, замкнутая гладкая кривая (цикл), точка.
Если фазовая кривая, отвечающая решению , есть гладкая замкнутая кривая, то это решение — периодическая функция.

ПРИМЕР 2. Типы фазовых кривых.

Точка , в которой правая часть системы обращается в нуль,, называется положением равновесия системы. Положение равновесия называют также точкой покоя автономной системы.

ПРИМЕР 3. Точки покоя автономной системы.

Если в каждой точке области задан n-мерный вектор
,, то говорят, что в области G задано векторное поле. Запишем автономную систему второго порядка

в векторной форме:

где
,
Автономная система

полностью определяется заданием векторного поля
.
Действительно, в каждой точке

гладкой фазовой кривой

существует касательный вектор
(x'(t₀ ), y'(t₀ ))
равный (в силу системы) вектору
,
иными словами, векторное поле

автономной системы задает в каждой точке направление касательной к фазовой кривой системы, проходящей через эту точку.
Точки векторного поля, в которых вектор — нулевой, называют особыми точками векторного поля. Таким образом, точки покоя автономной системы — это особые точки векторного поля.

ПРИМЕР 4. Векторное поле автономной системы.

Исправляем ошибки: Нашли опечатку? Выделите ее мышкой и нажмите Ctrl+Enter

Видео:Дифференциальные уравнения 6. Фазовые траектории. Особые точки автономных системСкачать

Понятие о фазовом пространстве. Метод фазовой плоскости

Страницы работы

Содержание работы

Лекция 11.Понятие о фазовом пространстве. Метод фазовой плоскости.

Фазовое пространство, или пространство состояний системы, это n—мерное пространство, координатами в котором являются фазовые переменные (переменные состояния) системы. Размерность фазового пространства соответствует размерности системы, то есть порядку системы дифференциальных уравнений в нормальной форме (форме Коши), описывающих данную систему.

В общем случае для нелинейной системы такая модель имеет вид:

i=1,2. n, (11.1)

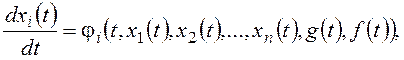
где j_i – нелинейные функции; x_i – фазовые переменные системы; g, f– задающее и возмущающее воздействия (возможно, векторные функции).

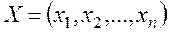
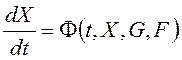
Если использовать вектор фазовых переменных , можно записать эту модель в векторной форме:

. (11.2)

Аргумент t в уравнениях (11.1)-(11.2) присутствует только для нестационарных систем.

В n—мерном фазовом пространстве (рис. 51) начальному моменту времени для процесса в системе t₀ соответствует точка, отображающая начальное состояние системы X 0 =(x₁₀,x₂₀,…,x_n₀). Каждому последующему моменту времени t>t₀ будет соответствовать другая точка, координаты которой – текущие значения фазовых переменных. Ее называют изображающей точкой. Решению же уравнений (11.1)-(11.2) x_i(t), i=1,2. n, соответствует некоторая непрерывная кривая, которую называют фазовой траекторией процесса в системе. Стрелкой на фазовой траектории показывают направление увеличения времени.

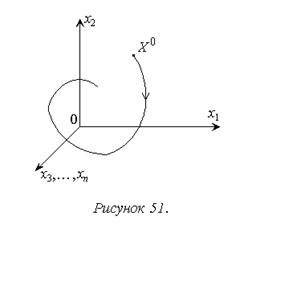
Дополнительно отметим, что значения правых частей уравнений (11.1) дают проекции вектора скорости движения изображающей точки по фазовой траектории для любого рассматриваемого момента времени.

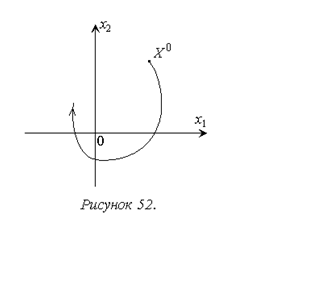
Для решения практических задач использовать отображение процесса в системе в многомерном фазовом пространстве, как правило, не удается. Поэтому наиболее распространенным вариантом использования рассматриваемого аппарата является метод фазовой плоскости, когда рассматриваются только две переменные состояния системы и фазовые траектории представляют собой плоские кривые (рис. 52). Очевидно, метод фазовой плоскости позволяет получить полную картину процесса только для систем второго порядка. Для таких систем он в основном и применяется.

В большинстве случаев при использовании метода фазовой плоскости входные сигналы g и f принимают равными нулю и рассматривают процессы, вызванные начальными отклонениями фазовых переменных от установившихся значений. Для стационарной системы второго порядка система уравнений (11.1) при этом примет вид:

. (11.3)

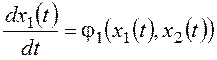
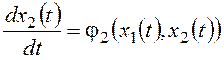
Совокупность фазовых траекторий, полученных для различных начальных условий, называют фазовым портретом системы.

Отметим, что при использовании математической модели системы физический смысл фазовых переменных не учитывается. Поэтому даже для системы второго порядка формально могут рассматриваться различные пары (x₁, x₂) с соответствующими заменами переменных в уравнениях (11.3). Выбор фазовых переменных проводится в зависимости от решаемой задачи для удобства ее решения.

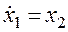
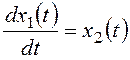
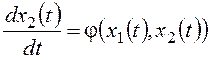
Наиболее распространенный вариант выбора фазовых переменных предусматривает непосредственную связь между ними следующего вида . Тогда уравнения (11.3) упрощаются:

. (11.4)

Удобство такой модели при использовании метода фазовой плоскости определяется тем, что для нее вертикальная координата является производной от горизонтальной. Вследствие этого фазовые траектории подчиняются следующим правилам:

1. В верхней полуплоскости движение изображающей точки по фазовой траектории возможно только слева направо, в нижней — только в обратном направлении.

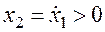
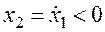
Объясняется это правило тем, что для верхней полуплоскости , то есть при нахождении здесь изображающей точки ее горизонтальная координата обязательно увеличивается. Для нижней полуплоскости и справедливо обратное.

2. Фазовые траектории пересекают горизонтальную ось только под прямым углом.

В точках пересечения с горизонтальной осью 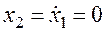, то есть при пересечении оси горизонтальная координата изображающей точки не изменяется, и касательная к фазовой траектории направлена вертикально.

3. Фазовые траектории не могут пересекаться.

Это правило справедливо для систем второго порядка при любом выборе фазовых переменных, если только уравнения системы не содержат переменных во времени входных сигналов. Во всяком случае, оно справедливо для моделей вида (11.3)-(11.4), которые для любой точки фазового пространства дают однозначные значения составляющих вектора скорости движения изображающей точки.

Рассмотрим некоторые примеры, демонстрирующие связь фазовых траекторий с временными характеристиками и основанный на ней способ построения фазовых траекторий.

Для колебательного звена с передаточной функцией

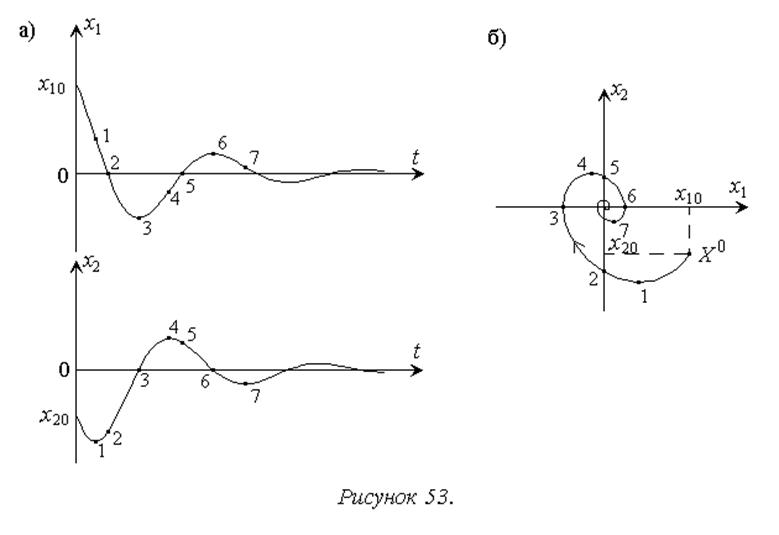
при отсутствии входного сигнала состояние равновесие устойчиво и совпадает с началом координат, переходный же процесс возбуждается начальными условиями для выходного сигнала и его производной, которые обозначим соответственно x₁ и x₂. Законы изменения x₁ и x₂ показаны на рис. 53а. На их графики нанесены точки, соответствующие экстремумам и нулям рассматриваемых функций. Соответствующие точки являются основой для построения фазовой траектории на плоскости с координатами x₁ и x₂ (рис. 53б).

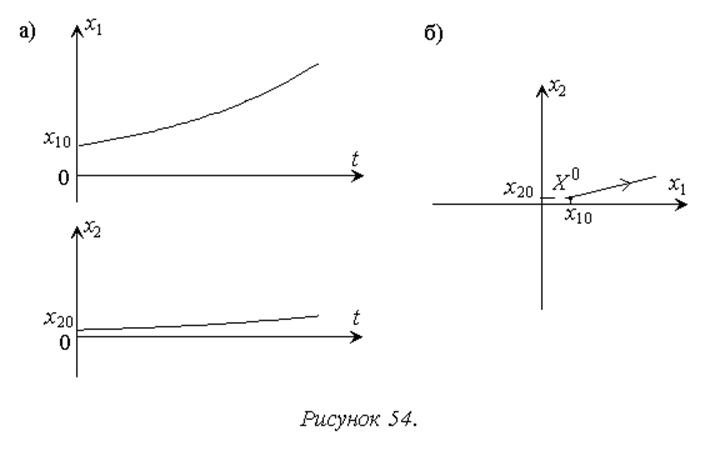
Ниже приведено аналогичное построение для неустойчивого апериодического звена с передаточной функцией .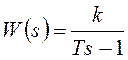

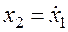
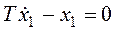
В качестве фазовых координат выбираются выходной сигнал звена x₁ и его производная . При отсутствии входного сигнала рассматривается процесс, инициируемый начальными условиями. Дифференциальное уравнение звена примет вид:

Его решение: Tp-1=0, , .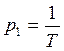

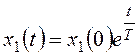
Закон изменения производной получим дифференцированием:

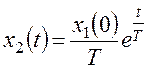
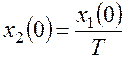
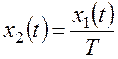
Таким образом, вертикальная координата начальной точки для фазовой траектории: , а уравнение фазовой траектории является уравнением прямой, проходящей через начало координат: . Фазовая траектория показана на рисунке 54.

Вернемся к системе уравнений (11.3). Состояниям равновесия системы соответствует постоянство фазовых переменных, то есть обращение в ноль их производных. Для линейной системы возможно только одно состояние равновесия. У нелинейной системы их может быть несколько. Каждому состоянию равновесия соответствует некоторая точка на фазовой плоскости.

На основе (11.3) может быть получено единое дифференциальное уравнение фазовой траектории:

. (11.5)

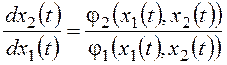
Его правая часть дает угол наклона касательной к фазовой траектории, то есть направление вектора скорости изображающей точки. Это справедливо для любой точки фазовой плоскости, за исключением точек, соответствующих состояниям равновесия. Для них правые части уравнений (11.3) обращаются в ноль, и в правой части уравнения (11.5) возникает неопределенность. Поэтому такие точки называют особыми точками на фазовой плоскости.

Рассмотренный выше способ построения фазовых траекторий требует получения законов изменения фазовых переменных x₁(t) и x₂(t). Это обеспечивается путем решения систем уравнений вида (11.4) или (11.5). Для нелинейных систем здесь в большинстве случаев требуется применение приближенных численных методов. При этом построение фазового портрета системы связано с многократным решением уравнений.

Поэтому часто более удобным оказывается анализ особых точек и особых линий на фазовой плоскости, позволяющий составить достаточно полное представление о фазовом портрете и отражаемых им свойствах системы.