Теория и примеры решения функциональных уравнений
Просмотр содержимого документа
«Элементарное введение в функциональные уравнения»
1.Функциональные уравнения. Их свойства и методы решения. 5
1.1 Определение и примеры функциональных уравнений. 5
1.2 Методы решения функциональных уравнений. 8
2. Решение функциональных уравнений Коши на множестве Q рациональных чисел. 13
2.1 Решение уравнения вида f(x+y)=f(x)+f(y) на Q. 13
2.2 Решение уравнения вида f(x+y)=f(x)∙f(y) на Q. 15
2.3 Решение уравнения вида f(x∙y)=f(x)+f(y) на Q. 17
2.4 Решение уравнения вида f(x∙y)=f(x)∙f(y) на Q. 19
3. Решение функциональных уравнений Коши на R. 22
3.1 Решение уравнения вида f(x+y)=f(x)+f(y) на оси R. 22
3.2 Решение уравнения вида f(x+y)=f(x)∙f(y) на оси R. 23
4. Решение функциональных уравнений Коши в измеримых функциях. 25
5. Класс уравнений типа Коши. 27
Список использованных источников. 30
Курсовая работа посвящена изучению функциональных уравнений, весьма общему классу уравнений, в которых искомой является некоторая функция.
К функциональным уравнениям по существу относятся дифференциальные уравнения, интегральные уравнения, уравнения в конечных разностях; следует, однако, отметить, что название функциональные уравнения обычно не относят к уравнениям этих типов. Под функциональными уравнениями в узком смысле слова понимают уравнения, в которых искомые функции связаны с известными функциями одного или нескольких переменных при помощи операции образования сложной функции. Функциональные уравнения можно также рассматривать как выражение свойства, характеризующего тот или иной класс функций.
Функциональное уравнение — это уравнение, в котором неизвестными являются функции (одна или несколько). Например,
Некоторые функциональные уравнения знакомы нам еще из школьного курса это f(x) = f(-x), f(-x) = — f(x), f(x+T) = f(x), которые задают такие свойства функций, как чётность, нечётность, периодичность.
Задача решения функциональных уравнений является одной из самых старых в математическом анализе. Они появились почти одновременно с зачатками теории функций. Первый настоящий расцвет этой дисциплины связан с проблемой параллелограмма сил. Ещё в 1769 году Даламбер свёл обоснование закона сложения сил к решению функционального уравнения
(1)
То же уравнение и с той же целью было рассмотрено Пуассоном в 1804 году при некотором предположении аналитичности, между тем как в 1821 году Коши (1789 – 1857) нашёл общие решения
Ряд геометрических задач, приводящих к функциональным уравнениям, рассматривал английский математик Ч. Баббедж (1792—1871). Он изучал, например, периодические кривые второго порядка, определяемые следующим свойством для любой пары точек кривой: если абсцисса второй точки равна ординате первой, то ордината второй точки равна абсциссе первой. Пусть такая кривая является графиком функции у = f(х); (х, f(х)) — произвольная ее точка. Тогда, согласно условию, точка с абсциссой f(х) имеет ординату х. Следовательно,
(2)
Функциональному уравнению (2) удовлетворяют, в частности, функции: ,
1. Функциональные уравнения. Их свойства и методы решения
1.1 Определение и примеры функциональных уравнений
Функциональные уравнения — весьма общий класс уравнений, в которых искомой является некоторая функция. К функциональным уравнениям, по существу, относятся дифференциальные уравнения, интегральные уравнения, уравнения в конечных разностях. Следует, однако, отметить, что название «функциональные уравнения» обычно не относят к уравнениям этих типов. Под функциональными уравнениями в узком смысле слова понимают уравнения, в которых искомые функции связаны с известными функциями одного или нескольких переменных при помощи операции образования сложной функции. Функциональные уравнения можно также рассматривать как выражение свойства, характеризующего тот или иной класс функций.
Например, функциональное уравнение f (x) = f (-x) характеризует класс чётных функций, функциональное уравнение f(-x) = -f(x) – класс нечетных; функциональное уравнение f (x + 1) = f (x) — класс функций, имеющих период 1, и т.д.
Одним из простейших функциональных уравнений является уравнение
f (x + у) = f (x) + f (y).
Непрерывные решения этого функционального уравнения имеют вид:
Однако в классе разрывных функций это функциональное уравнение имеет и иные решения. С рассмотренным функциональным уравнением связаны
f (x + у) = f (x) f (y),
непрерывные решения которых имеют соответственно вид e Cx , C∙lnx, x a (x 0).
Т.о., эти функциональные уравнения могут служить для определения показательной, логарифмической и степенной функций. В теории аналитических функций функциональные уравнения часто применяются для введения новых классов функций.
Например, двоякопериодические функции характеризуются функциональными уравнениями:
f (z + а) = f (z) и f (z + b) = f (z),
автоморфные функции — функциональными уравнениями:
где <sa> — некоторая группа дробно-линейных преобразований.
Если функция известна в некоторой области, то знание для неё функционального уравнения позволяет расширить область определения этой функции. Например, функциональное уравнение f (x + 1) = f (x) для периодических функций позволяет определить их значение в любой точке по значениям на отрезке [0, 1]. Этим часто пользуются для аналитического продолжения функций комплексного переменного. Например, пользуясь функциональным уравнением Г (z + 1) = z∙Г (z) и зная значения гамма-функции Г(z) в полосе 0 Re z
Условия симметрии, имеющиеся в какой-либо физической задаче, обусловливают определённые законы преобразования решений этой задачи при тех или иных преобразованиях координат. Этим определяются функциональные уравнения, которым должно удовлетворять решение данной задачи. Значение соответствующих функциональных уравнений во многих случаях облегчает нахождение решений.
Решения функциональных уравнений могут быть как конкретными функциями, так и классами функций, зависящими от произвольных параметров или произвольных функций.
Для некоторых функциональных уравнений общее решение может быть найдено, если известны одно или несколько его частных решений. Например, общее решение функционального уравнения
где j(x) — произвольная функция, а w(x) — частное решение этого функционального уравнения
Для решения функциональных уравнений их во многих случаях сводят к дифференциальным уравнениям. Этот метод даёт лишь решения, принадлежащие классу дифференцируемых функций.
Другим методом решения функциональных уравнений является метод итераций. Этот метод даёт, например, решение уравнения Абеля:
где a(x) — заданная функция и связанного с ним уравнения Шрёдера:
А. Н. Коркин доказал, что если a(х) — аналитическая функция, то уравнение Абеля имеет аналитическое решение. Эти результаты, нашедшие применение в теории групп Ли, привели в дальнейшем к созданию теории итераций аналитических функций. В некоторых случаях уравнение Абеля решается в конечном виде [1].
Видео:Функциональные уравнения ➜ Найдите f(x), если 2f(x+2)+f(4-x)=2x+5Скачать

Функциональные уравнения: Часть 1
Эта трилогия статьей будет посвящена функциональным уравнениям. В данной статье попытаемся понять что такое функциональное уравнение и с чем его едят. В следующих статьях рассмотрим конкретные методы решения более сложных функциональных уравнений(метод подстановок, и подобное).
Функциональное уравнение — уравнение, связующее значение функции в одной точке с её значениями в других точках.
Другими словами, в функциональных уравнениях место неизвестного занимает функция. Для примера, рассмотрим такое функциональное уравнение:
$$display$$2f(x)=2$$display$$ Тут интуитивно хочется разделить обе части уравнения на 2, что сработает и мы узнаем ответ: $$display$$2f(x)=2 Rightarrow f(x)=1$$display$$ Значит ответом на функциональное уравнение может быть только значение f(x), или похожее (это обычно указывают в условии задачи).
Рассмотрим некое функциональное уравнение, где с обоих сторон будут стоят функции. $$display$$4f(x)=2f(x)+2x Rightarrow 2f(x)=f(x)+x Rightarrow f(x)=x$$display$$ Стоит отметить что функция всегда имеет под собой число ($inline$f(x)=x+2, f(1)=3, f(5)=7$inline$, а значит можно производить над ними арифметические операции. Давайте рассмотрим функциональное уравнение из двумя переменными. Задание : найти все функции $inline$f: mathbb rightarrow mathbb$inline$ для каких $inline$4f(x+y)=f(x)+f(y)+2$inline$. В случаях из двумя переменными необходимо припустить что $inline$x=y=0$inline$, из этого мы узнаем значение $inline$f(0)$inline$.
$inline$x=y=0$inline$
$inline$4f(0)=2f(0)+2$inline$
$inline$2f(0)=2 Rightarrow f(0)=1$inline$
Узнав значение $inline$f(0)$inline$, приравниваем $inline$y$inline$ к нулю. Таким образом узнаем значение $inline$f(x)$inline$
$inline$y=0$inline$
$inline$4f(x)=f(x)+f(0)+2$inline$
$inline$3f(x) = 3 Rightarrow f($inline$f(x)=kx$inline$x)=1 $inline$
Ответ: $inline$ f(x)=1 $inline$
При такого вида уравнениях обязательно необходимо предполагать что $inline$x=y=0$inline$, но не всегда $inline$x=0vee y=0$inline$. Существуют такие аналоги как: $inline$x=y, x=f(y), . $inline$. К примеру, $inline$4f(x-y)=f(x)+f(y)+2$inline$. Подставляем $inline$x=y=0$inline$, получаем $inline$4f(0)=2f(0)+2 Rightarrow f(0)=1$inline$, тогда $inline$x=y$inline$ значит $inline$4f(0)=2f(x)+2$inline$, разделим обе части уравнения на 2 получим что $inline$2f(0)=f(x)+1 Rightarrow f(x)=1+2f(0) Rightarrow f(x)=3$inline$, произведем проверку, которая показывает что $inline$f(x)=3$inline$ есть решением данного функционального уравнения.
Теорема 1. Функциональное уравнение Коши $inline$f(x+y)=f(x)+f(y)$inline$ удовлетворяют все линейные функции вида $inline$f(x)=kx$inline$ (1)
Теорема 2. Функциональное уравнение $inline$f(x+y)=f(x)f(y)$inline$ удовлетворяют все показательные функции вида $inline$f(x)=k^$inline$ (2)
Теорема 3. Функциональное уравнение $inline$f(xy)=f(x)+f(y)$inline$ удовлетворяют все логарифмические функции вида $inline$f(x)=log_k (x)$inline$ (3)
Теорема 4. Функциональное уравнение $inline$f(xy)=f(x)f(y)$inline$ удовлетворяют все степенные функции вида $inline$f(x)=x^$inline$ (4)
Доведем их.
$$display$$(1) f(x+y)=a(x+y), f(x)+f(y) = ax+ay Rightarrow f(x+y)=f(x)+f(y)$$display$$
$$display$$(2) f(x+y)=a^, f(x)f(y) = a^a^ Rightarrow f(x+y)=f(x)f(y)$$display$$
$$display$$(3) f(xy)=log_a (xy), f(x)+f(y)=log_a(x)+log_a(y) Rightarrow f(xy)=f(x)+f(y)$$display$$
$$display$$(4) f(xy)=(xy)^, f(x)f(y) = x^y^ Rightarrow f(xy)=f(x)f(y)$$display$$
Теорема 5. Уравнения Йенсена $inline$f(frac)=frac, f(x)=kx+b$inline$, доводиться аналогично предыдущим.
Рассмотрим такую задачу: Найдите все линейные функции вида $inline$f(x)=ax, $inline$$inline$f: mathbb rightarrow mathbb$inline$ для которых правильно $inline$4(f(x-y)+f(x+y)+1)=2f(x)+f(y-1)$inline$.
Воспользуемся теоремой 1.
$inline$4(f(x-y)+f(x+y)+1) = 4(f(x)-f(y)+f(x)-f(y)+1) = 4$inline$
$inline$4=2f(x)+f(y-1)$inline$
Тут ключевой момент. Нельзя подставлять $inline$x=y=0$inline$, так как ничего не получиться. Необходимо подставить $inline$x=0, y=x+1$inline$, тогда мы сможем узнать $inline$f(0)$inline$.
$$display$$4=2f(0)+f(0) Rightarrow 4=3f(0) Rightarrow f(0)=frac$$display$$. Тогда подставляем $inline$x=y-1$inline$, и получаем $inline$4=2f(x)+f(x) Rightarrow 4=3f(x) Rightarrow f(x)=frac$inline$
Ответ: $inline$f(x)=frac$inline$
Видео:Разностное функциональное уравнение решено двумя способами.Скачать

Исследовательская работа «Функциональные уравнения»
В работе рассматриваются понятие функционального уравнения, история их изучения, способы решения и практическое применение. Актуальность работы заключается в том, что эта тема в школьном курсе математики не изучается в виду её сложности, а при поступлении в престижные ВУЗы, на предметных олимпиадах такие задачи встречаются.
Видео:Как решить функциональное уравнение f(x)+f(1/(1−x))=x, где f(x) определена везде, кроме точек 0 и 1?Скачать

Скачать:
| Вложение | Размер |
|---|---|
| funktsionalnye_uravneniya.zip | 2.42 МБ |
Видео:Старт Интенсива по функциональным уравнениям | Функциональные уравнения-1. Основные приёмыСкачать

Предварительный просмотр:
МБОУ «Средняя общеобразовательная школа № 11 с углубленным изучением отдельных предметов ЗМР РТ»
Автор работы: Багаутдинова Альбина,
ученица 11 «А» класса СОШ № 11
Научный руководитель: Петрова Ирина Владимировна,
I. Понятие функционального уравнения. 4
II. Способы решения функциональных уравнений. 6
- Простейшие функциональные уравнения. 6
- Решение функциональных уравнений методом подстановки. 7
- Решение функциональных уравнений методом Коши. 16
- Использование значений функции в некоторых точках. 18
- Уравнение относительно f(x). 19
- Графическое решение функциональных уравнений. 19
Список использованной литературы………………………………. ….. 22
Одно из важнейших математических умений, которым должны овладеть учащиеся средней школы, − умение решать уравнения. Корень уравнения находят в одно или более действий, многие текстовые задачи решаются алгебраическим способом, то есть уравнения одновременно сами по себе являются задачами и способами решения задач, умение решать которые необходимы всем учащимся школы. Но во время решения тренировочных заданий мне попалось уравнение, которое я решить не смогла. Как я узнала позже от учителя, это было функциональное уравнение.
Что же такое функциональные уравнения? И какие способы их решения существуют? Эти вопросы заинтересовали меня, и я решила провести исследование.
Актуальность работы заключается в том, что эта тема в школьном курсе математики не изучается в виду её сложности, а при поступлении в престижные ВУЗы, на олимпиадах, в заданиях части С ЕГЭ такие задачи встречаются.
Цель работы — выяснить, что является функциональным уравнением, найти способы решения и научиться применять их на практике.
1. Изучение и анализ литературы;
2. Поиск способов решения функциональных уравнений;
3.Применение полученных знаний при решении функциональных уравнений.
Структура работы: введение, понятие функционального уравнения, способы решения функциональных уравнений, примеры решения функциональных уравнений, заключение.
- Понятие функционального уравнения
Функциональное уравнение – это уравнение, которое содержит одну или несколько неизвестных функций (с заданными областями определения и значений).
Функция f(x) называется решением данного функционального уравнения, если она удовлетворяет ему при всех значениях аргумента в области её определения.
Решить функциональное уравнение – это, значит, найти все функции, которые тождественно ему удовлетворяют.
Функциональные уравнения возникают в самых различных областях математики, обычно в тех случаях, когда требуется описать все функции, обладающие заданными свойствами. Термин функциональное уравнение обычно используется для уравнений, несводимых простыми способами к алгебраическим уравнениям. Эта несводимость чаще всего обусловлена тем, что аргументами неизвестной функции в уравнении являются не сами независимые переменные, а некоторые данные функции от них.
Некоторые функциональные уравнения знакомы нам еще из школьного курса. Это уравнения f(x) = f(-x), f(-x) = — f(x), f(x+T) = f(x), которые задают такие свойства функций, как чётность, нечётность, периодичность. Простым видом функциональных уравнений является реккурентное соотношение , знакомое нам по теме Последовательности, которое , говоря формально, содержит неизвестную функцию от целых чисел и оператор сдвига . ( пример реккурентного соотношения: ).
Задача решения функциональных уравнений является одной из самых старых в математическом анализе. Они появились почти одновременно с зачатками теории функций. Первый настоящий расцвет этой дисциплины связан с проблемой параллелограмма сил. Ещё в 1769 году Даламбер свёл обоснование закона сложения сил к решению функционального уравнения
То же уравнение и с той же целью было рассмотрено Пуассоном в 1804 году при некотором предположении аналитичности, между тем как в 1821 году Коши (1789 – 1857) нашёл общие решения этого уравнения, предполагая только непрерывность f(x):
Даже известная формула неевклидовой геометрии для угла параллельности
была получена Н. И. Лобачевским (1792 – 1856) из функционального уравнения
которое он решил методом, аналогичным методу Коши. Это уравнение можно привести к уравнению
Ряд геометрических задач, приводящих к функциональным уравнениям, рассматривал английский математик Ч. Баббедж (1792—1871). Он изучал, например, периодические кривые второго порядка, определяемые следующим свойством для любой пары точек кривой: если абсцисса второй точки равна ординате первой, то ордината второй точки равна абсциссе первой. Пусть такая кривая является графиком функции у = f(х) ; (х, f(х)) — произвольная ее точка. Тогда, согласно условию, точка с абсциссой f(х) имеет ординату х. Следовательно,
Функциональному уравнению (3) удовлетворяют, в частности, функции:
Одними из простейших функциональных уравнений являются уравнения Коши
Эти уравнения Коши подробно изучил в своём (Курсе Анализа), изданном в 1821 году. Непрерывные решения этих четырёх основных уравнений имеют соответственно вид
В классе разрывных функций могут быть и другие решения. Уравнение (4) ранее рассматривалось Лежандром и Гауссом при выводе основной теоремы проективной геометрии и при исследовании гауссовского закона распределения вероятностей.
Функциональное уравнение (4) было опять применено Г. Дарбу к проблеме параллелограмма сил и к основной теореме проективной геометрии; его главное достижение − значительное ослабление предположений. Мы знаем, что функциональное уравнение Коши (4) характеризует в классе непрерывных функций линейную однородную функцию f(x) = ax . Дарбу же показал, что всякое решение, непрерывное хотя бы в одной точке или же ограниченное сверху (или снизу) в произвольно малом интервале, также должно иметь вид f(x) = ax. Дальнейшие результаты по ослаблению предположений следовали быстро один за другим (интегрируемость, измеримость на множестве положительной меры и даже мажорируемость измеримой функцией). Возникает вопрос: существует ли хоть одна какая-нибудь аддитивная функция (т. е. удовлетворяющая (4)), отличная от линейной однородной. Найти такую функцию действительно нелегко! В ходе работы мы покажем, что при рациональных x значения любой аддитивной функции должны совпадать со значениями некоторой линейной однородной функции, т. е. f(x) = ax для x Q. Казалось бы, что тогда f(x) = ax для всех действительных x. Если f(x) — непрерывна, то это действительно так, если же данное предположение отбросить — то нет. Первый пример отличного от f(x) = ax разрывного решения функционального уравнения (4) построил в 1905 году немецкий математик Г. Гамель с помощью введённого им базиса действительных чисел.
Многие функциональные уравнения не определяют конкретную функцию, а задают широкий класс функций, т. е. выражают свойство, характеризующее тот или иной класс функций. Например, функциональное уравнение f(x+1) = f(x) характеризует класс функций, имеющих период 1, а уравнение f(1+x) = f(1-x) — класс функций, симметричных относительно прямой x = 1 , и т. д.
- Способы решения функциональных уравнений
2.1 Простейшие функциональные уравнения
Решение простейших функциональных уравнений основано на применении простейших свойств различных функций.
Рассмотрим примеры решения простейших функциональных уравнений и неравенств.
1. Пусть функция у =f(х) возрастает на R. Решите:
а) уравнение f(3х + 2) = f(4х 2 + х);
б) неравенство f(3х – 48) ≤ f(-х 2 + х).
а) f(3х + 2) = f(4х 2 + х)
Есть такая теорема: если функция возрастает (убывает) на промежутке Х, то каждое своё значение она принимает в единственной точке. Поэтому,
х 1 =1 и х 2 = -0,5
Ответ: х 1 =1 и х 2 = -0,5.
б) f(3х – 48) ≤ f(-х 2 + х);
2. Пусть функция у =f(х) убывает на R. Решите неравенство
Решаем также как и в предыдущем задании, только меняем знак у неравенства, так как функция убывает на R.
3. Решить для всех где f принимает вещественные значения .
Положим : . Тогда и .
Теперь, положим :
Квадрат вещественного числа неотрицателен, и сумма неотрицательных чисел равна нулю тогда и только тогда когда оба числа равны 0. Значит для всех x и является единственным решением этого уравнения.
Ответ: х = 0, у = 0.
- Решение функциональных уравнений методом подстановки
Заменяя некоторые переменные функционального уравнения либо конкретными значениями, либо какими-либо другими выражениями пытаемся либо упростить это уравнение, либо привести его к такому виду, что дальнейшее решение станет очевидным. Особенность применяемого метода как раз и состоит в том, что в ряде случаев он позволяет отыскать решения в классе всевозможных функций.
1. Найдите все функции, определённые на множестве , удовлетворяющие соотношению .
Придадим x значение . Получим
Из уравнения (1) выразим и подставим в уравнение (2).
Проверим, действительно ли функция f(x) удовлетворяет уравнению .
2. Найти функцию, удовлетворяющую уравнению
2) Подставим в исходное уравнение, получим
3)Заменим z на получим
или после преобразований в правой части уравнения:
4)Итак, получили два уравнения:
5)Умножим обе части 1-го уравнения на (-2) и сложим со 2-ым уравнением, получим:
3. Пусть — некоторое действительное число. Найти функцию f(x) , определённую для всех x ≠ 1 и удовлетворяющую уравнению
,где g – заданная функция, определённая при x ≠ 1 .
Решение: При замене
решением которой при a 2 ≠ 1 является функция
4. Найти решение системы функциональных уравнений относительно неизвестных функций f(x) и g(x) :
В первом уравнении сделаем подстановку 2x = 1/z .
и первое уравнение принимает вид:
В результате получаем систему уравнений:
решение которой g(x) = 1/x, f(x) = x+1 .
Ответ: g(x) = 1/x, f(x) = x+1.
5. Найдите все функции f: R R , которые при всех х, у € R удовлетворяют уравнению f(х+у)=х+уf(х)+(1-х)у . (1)
Пусть f − функция удовлетворяющая уравнению (1). Поскольку (1) выполняется при всех значениях переменных х и у , то оно будет выполнятся и при конкретных значениях этих переменных. Подставив, например, у = 0 в исходное уравнение, мы получим f(х)=х. Это равенство должно выполнятся при любом действительном х .
Таким образом, (1) => f(х)≡х или, иными словами, никакая функция кроме f(х)≡х не может удовлетворять уравнению (1). Это, тем не менее, не доказывает, что функция f(х)≡х является решением функционального уравнения (1). Непосредственная проверка показывает, что найденная функция действительно удовлетворяет уравнению при всех х,у € R .
6. Найдите все функции f: R R , которые при всех х, у € R удовлетворяют уравнению f(х+у)=х+уf(х)+(1-sin х)у . (2)
Точно также, как и в предыдущей задаче, устанавливаем, что для функции f, которая удовлетворяет (2), должно выполнятся тождество f(х)≡х. Однако, подставив функцию f(х)=х в (2), мы тождества не получим. Поскольку никакие другие функции также не могут быть решениями (2), то данное уравнение решений не имеет.
- Найдите все функции f: R R , которые при всех х, у € R удовлетворяют уравнению
f(х+у 2 +2у+1) = у 4 +4у 3 +2ху 2 +5у 2 +4ху+2у+х 2 +х+1. (3)
Поскольку мы хотим получить значение f(х) , попробуем избавится от слагаемого у 2 +2у+1 под знаком функции. Уравнение у 2 +2у+1=0 имеет одно решение у=-1 . Подставляя у= -1 в (3) получаем f(х)= х 2 -х+1 .
Ответ: f(х)= х 2 -х+1.
- Найдите все функции f: R R , которые при всех х, у € R удовлетворяют уравнению
f((х 2 +6х+6)у)=у 2 х 4 +12у 2 х 3 +48у 2 х 2 -4ух 2 +72у 2 х-24ух+36у 2 -24 (4)
Как и в прошлой задаче, мы хотим получить под знаком функции свободную переменную ( х или у ). В данном случае, очевидно, проще получить у . Решив уравнение х 2 +6х+6)у=0 относительно х получаем х 1 = -1, х 2 = -5 . Подстановка любого из этих значений в (4) дает нам f(у)=у 2 -4у .
9. Решите следующие функциональные уравнения.
в) f(x+y)+f(x-y)=2f(x)cos y
а) Положим у=1/x. Тогда f(1/y) + 2f(y) =3/y и f(y)+2f(1/y)=3y. Отсюда f(y)= 2/y – y.
б) Положим y=x-1/x , затем z=y-1/y. Получим систему трёх линейных уравнений относительно f(x), f(y), f(z), з которой находим
в) Положив у=π/2, получаем f(х+π/2) +f(x-π/2)=0 для любого х, откуда f(x+π)= — f(x). Заменив у на у+π/2, получаем
заменив теперь х- π/2 на х, имеем:
и с учетом предыдущего:
Положив х=0, получаем отсюда и из исходного уравнения:
Таким образом, искомая функция должна иметь вид a cos y +b sin y, где a,b – константы.
Решение: 1 ) Заменим на , получим или .
2)Умножим обе части уравнения из п.1 на (-2) и сложим с исходным уравнением:
Решение: 1)Заменим в уравнении н а , получим 2 .
2) Умножим обе части исходного уравнения 2 на (-2) и сложим с уравнением 2 ,
1) Заменим в уравнени е на , .
2)Умножим уравнение н а и вычтем из уравнения , получим —
1)Заменим в уравнении на получим .
2)Выразим из исходного уравнения , получим
3)Подставим в уравнение , получим .
1.Заменим н а , получим
2.Умножим обе части уравнения на и вычтем из уравнения
Решение: 1)Пусть , тогда уравнение принимает вид:
2)Пусть тогда исходное уравнение принимает вид:
3)Умножим обе части уравнения из п.1 на 2, а обе части уравнения из п.2 на (-3) и почленно сложим получившиеся уравнения:
1) Замени м н а , получим или .
2)Умножим обе части уравнения из п.1 на (-2) и сложим с исходным уравнением:
2.3. Решение функциональных уравнений методом Коши
1. Найдите функцию , определённую на множестве натуральных чисел, удовлетворяющую условию , где d — некоторое действительное число.
Будем решать это уравнение по схеме, которая в математике называется методом Коши.
1. Найдём выражения для Получим , , .
2. Этот “эксперимент” подсказывает, что , где .
3. Проверим, действительно ли выполняется равенство , где . Применим для доказательства метод математической индукции.
1). Проверим, выполняется ли равенство при x=1 : — верно.
2). Предположим, что равенство верно при , где , т.е. — верно.
3). Докажем, что из этого следует равенство для x=n. Т.к. , то при x=n получим или ; . Значит, равенство верно для любого натурального n . Таким образом, решением заданного функционального уравнения будет функция , где f(1)- произвольное число.
2. Уравнение Коши
Найдите все непрерывные функции, удовлетворяющие условию .
Будем находить решение функционального уравнения постепенно, т.е. сначала найдём его решение, если является натуральным числом, затем – целым, потом рациональным и, наконец, — действительным.
1. Пусть y=x. Тогда .
2. При , получим , , …
3. Методом математической индукции доказываем, что при натуральных значениях . (1)
4. При x=1 получим . — постоянное число. Обозначим его через . Значит, для , имеем .
5. Положим в равенстве (1) , где , получим . Отсюда или . Обозначив через , получим . Значит, при положительном и рациональном x мы получим . Предполагая, что функция — непрерывна, получим , при , .
6. Возьмём в равенстве . Получим . Отсюда .
7. Возьмём в этом равенстве . Получим или .
Т.к. , то , т.е. . Итак, для любого действительного решением уравнения будет функция .
3. Найдите непрерывные функции , удовлетворяющие условию . (1)
Попробуем свести это уравнение к функциональному уравнению Коши с непрерывным решением . Пусть у=0 , тогда . Так как — постоянное число, обозначим его через и получим . Придадим теперь х значение . Получим . Из уравнения (1) получим или (2). Решением уравнения (1) является функция . Значит, решением уравнения (2) будет функция .
4. Найдите все непрерывные решения уравнений Коши:
a) f (хy) = f(x) + f(y) (x, y € R );
б) f(x + y) = f(xy) (x, y€ R);
в) f(x + y) = f(x)f(y) (x, y€. R).
a) Пусть вначале x > 0. Положим g(x) = f(e х ). Тогда g(x + y) = f(e х+у ) = f(e х e у ) = f(e х ) + f(e у ) =
=g(x) + g(y), т. е. g(x) удовлетворяет аддитивному уравнению Коши. Так как e х и f(x) непрерывны, то и g(x) непрерывна и имеет вид cx, где c- константа. Тогда f(x) имеет вид c ln x.
В частности, f(1) = 0. Положив x = y = -1, получаем f(1) = 2f(-1), откуда f(-1) = 0. Для произвольного x
б) Положив y = 0, получаем f(x) = f(0), т.е. f(x) ≡ const. Очевидно, что любая
в) Если f(x) = 0 для некоторого x, то f(z) = f(x)f(z-x) = 0 для любого z. В противном случае функция, будучи непрерывной, всюду имеет один и тот же знак. Так как f(2x) = (f(x)) 2 , то этот знак положителен и можно рассмотреть непрерывную
функцию g(x) := lnf(x). Имеем g(x+y) = ln(f(x)f(y)) = ln f(x)+ln f(y) = g(x)+g(y),
т.е. выполнено аддитивное уравнение Коши. Отсюда g(x) = cx для некоторого c, и
f(x) = e сх . Таким образом, либо f(x)≡ 0, либо f(x) ≡е сх .
- Использование значений функции в некоторых точках
Иногда бывает невозможно найти подстановку, которая бы значительно упрощала бы вид уравнения. Однако, если зафиксировать одну из свободных переменных, некоторые члены уравнения могут также оказаться фиксированными. Для них можно ввести удобные обозначения и использовать при решении как обычные константы. Если эти константы войдут в ответ, проверка покажет, какие их значения являются допустимыми.
1. Решить уравнение f(x+f(y))=xy.
Подстановка у=0 даёт f(x+f(0))=0 . На первый взгляд пользы мало, так как мы не знаем, чему равно f(0) . Обозначим f(0)=с , тогда получаем f(х+с)= 0. сделав замену переменной t=x+c (подстановка х=t-c ), получаем f(с)=0 , но такая функция, очевидно, не удовлетворяет исходному уравнению, поэтому решений нет.
2. Решить уравнение f(x+f(y))=x+у
Снова сделаем подстановку у=0 и обозначим с=f(0) , получим f(х+с)=х . Замена t=х+с дает f(t)=t-c . Несмотря, на то, что точное значение с нам известно, мы уже знаем, что лишь функция вида f(х)=х-с , где c=const , могут удовлетворять уравнению при всех х,у. чтобы найти с, подставим найденную функцию в исходное уравнение (заодно таким образом сделаем проверку):
Отсюда видим, что равенство f(x+f(y))=x+у для всех х,у при с = 0 и только при нем. Поэтому ответ f(x)=x.
- Решить уравнение f( x – f(y)) = x – y.
Решая это уравнение аналогично предыдущему, получим f(x) = x+c.
Если теперь сделать проверку, окажется, что
f(x — f(y)) = f(x — (y + c)) = (x — (y + c)) + c = x – y, для всех x; y; c € R .
Поэтому ответом будет семейство функций f ( x ) = x + c; c € R .
- Уравнение относительно f(x)
- Найти все f : R R такие, что (f(x))² = 1
Рассматривая это как уравнение относительно неизвестного f(х) , получаем
Может показаться, что ответом будут две функции, f(х)=1, f(х)=-1 . Однако, это не так. Рассмотрим, например функцию
Несложно видеть, что данная функция удовлетворяет уравнению. Какой же смысл придать совокупности? Поскольку исходное равенство должно выполнятся для всех х € R, то и совокупность также должна выполняться для всех х € R, то есть для каждого х имеет место одно из равенств. Однако, неверным будет предположение, что одно из равенств выполняется сразу для всех х. Как мы увидели на примере, для одних х может выполняться одно из равенств, а для других – другое.
Попробуем охарактеризовать множество функций, задаваемое данным уравнением. Пусть А – множество тех х , для которых выполнено первое равенство. Тогда для всех остальных х должно быть выполнено второе. Мы видим, что множество А однозначно задает функцию f:
Ответ: E(f) = , где Е(f) обозначает множество значений f.
- Найти все f: R R такие, что ( f ( x ) + f ( y ))² = ( x + y ) ² .
Подстановка x = y = 0 дает f(0) = 0.
Подставив теперь у = 0, получим (f(x))² = x² .
Как мы уже знаем, для каждого х € R существуют две возможности:
f(x) = x или f(x) = -x. Однако в этом случае не все функции f с f ( x ) = ± x
будут решениями. Именно докажем, что лишь функции (x) = x и f(x) = -x удовлетворяют данному условию. Если f не совпадает ни с одной из этих функций, то найдутся такие x; y ≠ 0, что f(x) = x, f(y) = -y . Тогда подставив их в исходное уравнение, получим (x-y)² = (x+y)², откуда следует, что xy = 0 . Получили противоречие. Остается проверить, что указанные функции удовлетворяют уравнению при всех х, у € R.
- Графическое решение функционального уравнения
При каких а и b для функции f(х)=a|x-b| +3a|x-b | выполнено условие при всех действительных х : f(х)=f(f(х)) ?
- При а=0 функция f(х)=0, и уравнение, очевидно, удовлетворяется.
- Пусть а>0, тогда при больших х>0 функция f(х)=а(х-b)+3a(x-b )=4ax-a(b+3b )>0
По рис.1 определяем, что возможно только равенство f(х)=х, если значения х достаточно велики и х>0. Конкретно, х>max.
Следовательно, возможные значения для параметров a и b определяются из системы:
которая имеет два решения:
При а=1/4, b=-1/3 получаем функцию
Ее график (рис.2) является графическим решением уравнения f(х)=f(f(х))
- Теперь предположим, что а
Следовательно, возможные значения для параметров а и b определяются из системы
которая имеет два решения
Если a=-1/4, b=0, то функция f(х)=-|х| удовлетворяет уравнению f(х)=f(f(х))
Если a=-1/4, b=-1/3, тогда получаем функцию
А вот ее график (рис. 3) не является графическим решением уравнения f(х)=f(f(х)).
Целью данной работы было изучение понятия Функциональные уравнения, поиск способов решения и их практическое применение. В результате проведенных исследований я пришла к выводу, что термин функциональное уравнение обычно используется для уравнений, несводимых простыми способами к алгебраическим уравнениям. Не зная методов их решения, решить их практически невозможно. Хотя функциональными уравнениями ученые – математики занимаются с очень давних пор, этому курсу так и не нашлось достойного места в школьных математических программах. А жаль. Ведь решение отдельных функциональных уравнений требует достаточно глубокого понимания предмета и прививает любовь к самостоятельной творческой работе.
Вопросы, рассмотренные в работе, не только расширяют кругозор, но и несут обучающую функцию, так как при поступлении в престижные Вузы, на олимпиадах, в заданиях части С ЕГЭ такие задачи встречаются, что только подчеркивает значимость выбранной темы.
📽️ Видео
Как решить функциональное уравнение f(x+f(y+xy))=(y+1)f(x+1)−1?Скачать

Интересное функциональное уравнение, или как я проучил барыгуСкачать

Функциональное уравнение 2f(1-x)+1=xf(x)Скачать

🚀Часть 1. Функциональные уравнения: Погружаемся глубже в математику🔮Скачать

Функциональное уравнение в явном виде (МехМат 2008)Скачать

Найти f(x). Функциональное уравнениеСкачать

Показательная зависимость 4. Функциональное уравнениеСкачать

Функциональное уравнение f(x+y)=f(x)f(y).Скачать

Функциональное уравнение для крепких. #математика #алгебра #олимпиада #функция #simplemathСкачать

Функциональное уравнение с американской олимпиадыСкачать

Функциональное уравнение на функцию двух переменных.Скачать
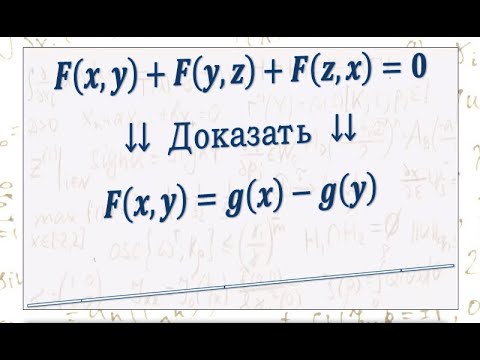
Функциональные уравнения (теория и примеры для ДВИ)Скачать

Решить функциональное уравнениеСкачать

Видеоквант: Функциональные уравненияСкачать

Функциональное уравнение 3f(2x+1)=f(x)+5x | Математический анализ | КАК РЕШАТЬ?Скачать

Математика 10 класс. Занятие 19. Функциональные уравненияСкачать

