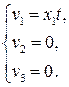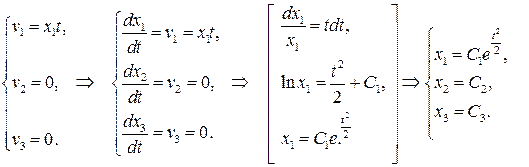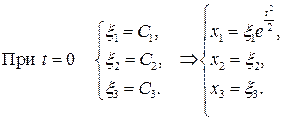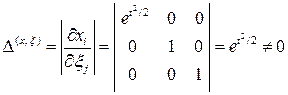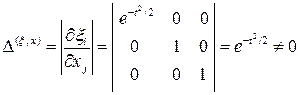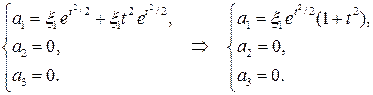Эйлеровы или лагранжевы координаты использованы при выводе уравнений буссинеска

Лекция 1 Лагранжево и эйлерово описание сплошной срелы

В конце приведены примеры и задачи

Просмотр содержимого документа
«Лагранжево и эйлерово описание сплошной срелы»

Сплошная среда. Описание

Сплошная среда– модель вещества, в которой распределение массы, сил, импульса, энергии(и их потоков) и всех параметров(плотностей, скоростей, перемещений, температур, давлений, напряжений и т.д.), определяет состояние и движение этого вещества, определяет непрерывно дифференцируемыми функциями по пространственным координатам и времени, заданных во всех точках рассматриваемого объема и во все моменты времени из рассматриваемого интервала за исключением отдельных поверхностей, линий или точек.

под материальной точкой в механике сплошной среды понимается частица среды (вещества) вокруг нее(точки) как центра масс, частица с характерным размером порядка δr, объемом δV=O((δr)3), массой ρδV. Причем ее размер с одной стороны очень мал по сравнению с харак-терным размером исследуемого процесса или тела (δr lat), т.е. указанная частица содержит огромное число молекул

Лагранжево и эйлерово описания сплошной среды

описать сплошную среду —значит задать ее числовые характеристики. Это м сделать, по кр мере,2 способами: привязывать х-ку к частице в данный мом времени и привяз х-ку к т пр-ва, в кот в данный момент нах частица. Эти 2 способа наз, соотв, лагранжевым и эйлеровым описанием спл среды. Таким обр, в лагранжевом подходе все х-ки задаются в переменных (x, t) О W₀ × R, а в эйлеровом — в переменных (x, t) О <W_t × <t>: t О R>. Соотв, координаты (x, t) называют лагранжевыми координатами (или переменными), а (x, t) — эйлеровыми.

Эти два описания, эквивалентны. Если известна некоторая характеристика F в лагранжевом описании, то м найти ее представление в эйлеровом, и наоборот. Например, если v L (x, t) и v E (x, t) — лагранжево и эйлерово представления скорости, то, очевидно, v L (x, t) = v E (g(x, t), t),), и, наоборот, v E (x, t) = v L (g – 1 (x, t), t).

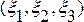
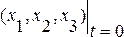
В качестве лагранжевых координат частицы обычно используют пространственные координаты т , в кот эта частица находится в нач момент времени

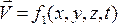
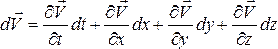
скорость жидкости в разл точках простран­ства д б функцией 4 перем х, у, z, t, назы­ваемых переменными Эйлера,, а ее дифференциал равняться

.

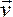
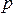
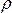
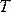
Движение сплошной среды и происходящие процессы описываются полями физических величин (скорости , давления , плотности , температуры и т.д.).

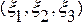
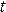
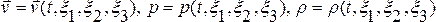
Лагранжев подход.Если эти величины рассматриваются как функции лагранж коорди-нат и времени , то описание называется лагранжевым или материальным. Т е, если и т. д., то это лагранж описание движения спл среды. При этом подходе события описываются как происходящие с индивидуальными частицами.

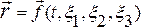
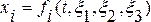
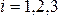
Основной кинематической характеристикой при лагранжевом описании является закон движения спл среды, т.е. зависимость пространственных координат от лагранжевых и времени: или в координатной записи , где .

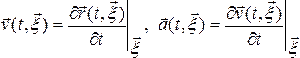
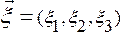
Тогда скорость и ускорение частиц сплошной среды опр соот: , где вектор .

скорость изменения нек величины в индивидуальной частице сплошной среды (т. е. при фиксированных значениях лагранжевых координат) называется индивидуальной, или матери-альной, или полной производной по времени от величины и обозначается

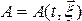
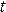
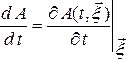
При лагранжевом описании (т.е., когда ) полная производная вел по времени по опред

В движущейся среде приращ dx, dy, dz не явл неза­висимыми, а соответственно равны

, , . Поэтому справедливо равенство:

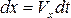
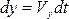
где – оператор Гамильтона (набла).Это озн, что полное ускорение индивиду жид­кой частицы, нах в момент времени t в т простр-­ва с коорди x, y, z, состоит из 2 частей: локального ускорения , обусловл изменением скорости по вре­мени в данной точке, и конвективного ускор , обусловл неоднородн поля скоростей в окрестности данной точки и связанного с этим обстоятельством конвективного переноса

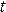
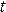
Эйлеров подход.При эйлеровом описании (пространств описании) физ величина рассм как ф пространств к-т и времени . При этом подходе события описываются как происхо-дящие в точке пространства. Основной кинематич х=кой при эйлеровом описании является поле скорости , где . Вектор скор — это скорость частицы спл среды, кот в мом нах в т пр-ва с к=тами .

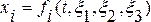
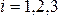
переход от лагранжева описания к эйлеровому, н соотн, выр закон движения , где , разрешить относительно лагранжевых координат, т. е. найти функции , где . Тогда для любой величины , лагранжево описание которой изв, эйлерово описание находится как сложная функция .

Переход от эйлерова опис к лагранжевому: ннайти реш системы обыкн дифф уравнений

, где 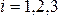(0.1.0) с нач усл .

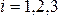
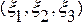
Получ реш , и есть закон движ спл среды, а — лагранжевы к-ты частиц. Тогда для любой вел , эйлерово опис кот изв, лагранж опис нах как сложная функция .

Выч полной произв 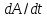вел по времени при эйлер опис ( т. е., когда ):

исп:опр закона движения среды , 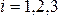,опре комп-т вектора скорости тогда по опр полной производной имеем:

т. е., ,или в сокр записи , где — вектор градиента вел , — вектор скорости среды.

Получ ф-ла для полной производной вел при эйлеровом описании м так: скорость изм вел в индивидуальной ч-це спл среды при эйлер опис= скорости изменения вел в той точке эйлерова пр=ва, в кот в данный момент находится индивид частица ( слаг ), плюс скорость изменения величины за счет переноса в данную т пространств изм вел в рез макроскопического движения сплощной среды (слаг )

. Производная Лагранжа (конвективная производная), —опред изм парам данной функции в т <displaystyle <vec >> в мом времени t при конвекции (движении среды с определённой скоростью <displaystyle <vec >(<vec >,t)> Явл одним из слаг производной Лагранжа (субстанциональной производной) и м б найд путём действия оператора <displaystyle (<vec >cdot nabla )> на скалярную либо векторную функцию (тут — оператор набла).

это производная, взятая в з-ти от с-мы координат, движущейся со скоростью u и часто исп в гидроаэромеханике и классич механике. Она определена как от скалярной функции координат и времени, так и от векторной :

где — это оператор набла, а обозначает частную производную по t.

Верно следующее тождество, когда берётся производная Лагранжа от интеграла:

Док-во через п-ло диф сложных функций для частных произв. В тензорной нотации (с согл суммир Эйнштейна), можно записать:

На примере поля плотности ρ и поля скоростей рассм некот общие характеристики полей.

Поле ρ = ρ(х_1; х₂, х₃), характеризующее данный процесс или движение, м б стационарным dρ/dt=0 (установившим) или нестационарным dρ/dt≠0 (неустановивш). Одно и то же движение м б как установивш, так и неустановивш, все зависит от выбора системы к-т, относит кот изучается движение. Поэтому установившееся (стационарное) движение — понятие относительное.

Для любого векторного поля используют понятие векторных линий.

Дано изменение температуры среды в эйлеровых координатах ,

Опр локальную производную по времени отв ∂T/∂t= — kV

определить конвективную производную. .Отв: Vxk

Задачи Эйлерово и лагранжево описание движения спл среды

пр 0 Для нек момента времени закон движения сплошной среды задан уравн:

Опр поле перемещ в лагранжевых и эйлеровых к-тах Опр обратный закон движения
. Перемещения , -радиусы-векторы текущего и начального положения.

в лагранжевых координатах

в эйлеровых координатах

Пр 1. Дано эйлерово описание движения сплошной среды

Требуется найти его лагранжево описание.

Реш.Зададим материальные координаты так, что в начальный момент движения они были равны геометрическим т.е. при . Учитывая определение скорости и начальные условия, имеем задачу Коши для системы уравнений

, .Решим эту задачу.

Закон движения в лагранжевых переменных найден.Таким обр, чтобы перейти от эйлерова опи-сания к лагранжевому, надо составить систему и решить ее с учетом начальных условий . Убедимся что и – взаимнооднозн зав-ти, т.е. в любой момент времени в любой точке пространства находится только 1 материальная частица. Для этого надо вычислить якобиан и убедиться, что он никогда не обращается в нуль.

для любого момента времени.

След, за-ть взаимнооднозначна. Известно что . Отсюда следует, что обратная зависимомть также взаимнооднозначна. В этом можно убедиться непосредственно, вычислив якобиан обратного преобразования

для любого момента времени.

Найдем выражение для скорости и ускорения в лагранжевых переменных. Чтобы выразить скорость, достаточно геометрические координаты заменить на материальные, используя для этого закон движения в лагранжевых переменных. Получим

Найдем ускорение, которое вычисляется как материальная производная скорости. (при лагранжевом описании материальная производная совпадает с частной производной по времени.

Пр2 Дано лагранж описание движения тогда эйлерова описание имеет вид

Дано плоское поле скоростей

найти закон движения частиц в лагранжевых переменных.

З 4.1.2.Дан лагранжев закон движения:

Найти компоненты скорости в эйлеровом описании.

З 4.1.3.Дан лагранжев закон движения:

1)Найти якобиан перехода к эйлер переменным. 2) Найти скорость в лагранжевых переменных.

3) Найти ускорение в лагранжевых переменных. 4) Перейти к эйлерову описанию (выр через ). 5) Найти якобиан перехода к лагранж перем. 6) Найти скорость и ускорение в эйлеровых переменных. 7) Зная поле скоростей в эйлеровых переменных перейти к лагранжевому описанию.

З 4.1.4.Задано поле скоростей в переменных Лагранжа:

1) Показать, что переход к перем Эйлера возможен. Найти компоненты скорости и ускорения в перем Эйлера. 2) Рассм поле скоростей в перем Эйлера, получ в п 1, как усл задачи, перейти к перем Лагранжа и получить закон движения.

З 4.1.8.Движение среды происходит по закону

Пров, что числа для индивид частицы имеют смысл коорд , , т пр-ва, в кот она нах в мом. Найти поля скорости и ускорения в лагранж описании. Какая частица в момент времени находится в т с коорд?

З 4.1.10.В момент рассм функции

обратные закону движения

Каков смысл их значений? Чему равны индивидуальные производные ?

З 4.1.11.Найти поля скорости и ускор в лагранжевом и эйлеровом описаниях, если движение среды происх по з-ну

а) трехосное растяжение тела:;

б) простой сдвиг:;

в) однородная деформация при одновременном вращении тела с закрепленной точкой:

З 4.1.12.Ввести лагранжевы координаты и найти закон движения сплошной среды, если оно происх с полем скорости

З 4.1.13.Ввести лагранжевы коорд и найти закон движ спл среды, если поле скорости имеет вид:

З 4.1.14.Задан закон движения сплошной среды

Показать, что траектории – окружности, а величины скорости постоянны. Определить связь между и и константами и .

З 4.1.15.Дано поле скоростей в лагранжевом описании

. Найти компоненты ускорения.

З 4.1.16.В каком случае и материальная производная нек параметра совпадает с частной производной этого параметра по времени?

5. Задано поле скоростей v1= x1+2×2, v2=4×1– x2, v3=0. Привести его через масштабы. Найти поле ускорений в эйлеровых переменных; опр законы движения частиц в эйлеровых и лагранжевых переменных; найти поля скорости и ускорений частиц в лагранжевых переменных.

З 4.1.17.В электромагнитном континууме напряженность магнитного поля , гдеи – конст, и движение задано полем скоростей. Определить скорость изменения напряженности магнитного поля для частицы, расположенной в момент в точке.

З 4.1.18.Напряженность электрического поля в облпсти, занятой движущейся жидкостью, , гдеи – конст. Скорость жидкости задана к-тами. Найтив т.

4) Х – лагранжева координата, х – эйлерова координата

4) Индивидуальный объем в виде линейного отрезка движется со скоростью v. Температура отрезка изменяется линейно от T_o до T_к и не меняется во времени. Описать изменение температуры отрезка с позиций Эйлера и Лагранжа.

Х – лагранжева координата, х – эйлерова координата. В начальный момент времени лагранжевы и эйлеровы координаты совпадают

Описание с позиций Лагранжа Описание с позиций Эйлера

, ,т.е. скорость с течен времени в лагражевых к-тах не меняется

Связь лагранжевых и эйлеровых координат в данной задаче , т.е.

Подставим это выражение в уравнение для температуры в лагранжевых координатах

Видео:Принцип наименьшего действия #2 - Уравнение Эйлера-ЛагранжаСкачать

Переход от эйлерова описания к лагранжевому и обратно

Эйлерово и лагранжево описание являются равносильными и нужно уметь переходить от одного описания к другому. Рассмотрим этот вопрос на примере.

Пример 1. Дано эйлерово описание движения сплошной среды

Требуется найти его лагранжево описание.

Решение.

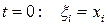
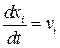
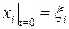
Зададим материальные координаты так, что в начальный момент движения они равны геометрическим, т.е. при . Учитывая определение скорости и начальное условие, имеем задачу Коши для системы уравнений

,

.

Решим эту задачу.

Закон движения в лагранжевых переменных найден.

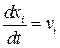
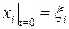
Таким образом, чтобы перейти от эйлерова описанию к лагранжевому, необходимо составить систему и решить ее с учетом начальных условий .

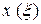
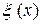
Убедимся, что и – взаимнооднозначные зависимости, т.е. в любой момент времени в любой точке пространства находится только одна материальная частица. Для этого нужно вычислить якобиан и убедиться, что он никогда не обращается в нуль.

для любого момента времени.

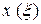
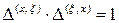
Следовательно, зависимость взаимнооднозначная. Известно, что . Отсюда следует, что обратная зависимость также взаимнооднозначная. В этом можно убедиться и непосредственно, вычислив якобиан обратного преобразования

для любого момента времени.

Найдем выражения для скорости и ускорения в лагранжевых переменных. Чтобы выразить скорость, достаточно геометрические координаты заменить на материальные, используя для этого закон движения в лагранжевых переменных. Получим

Найдем ускорение, которое вычисляется как материальная производная скорости. Напомним, что при лагранжевом описании материальная производная совпадает с частной производной по времени.

Пример 2. Дано лагранжево описание движения сплошной среды

Требуется найти его эйлерово описание.

Решение.

Учитывая определение скорости и начальное условие, имеем задачу Коши для системы уравнений:

,

.

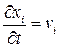
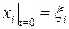
Подставим в систему заданное выражение для скорости и проинтегрируем по времени. Получим, проделав несложные выкладки, эйлерово описание:

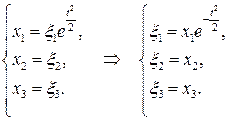
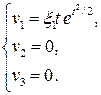
Найдем ускорение, которое вычисляется как материальная производная скорости :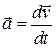

.

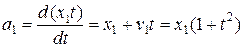
Можно вычислить иначе:

,

.

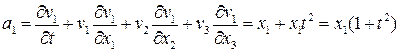
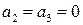
Третий путь состоит в том, чтобы вычислить ускорение в лагранжевых переменных (см. Пример 1), и потом заменить в его выражении материальные координаты на геометрические, как выше было сделано для скорости.

Видео:Уравнение ЛагранжаСкачать

Переменные Лагранжа и Эйлера

Видео:Уравнение касательной в точке. Практическая часть. 1ч. 10 класс.Скачать

Переменные Лагранжа и Эйлера

• Переменная Лагранжа. Для выбранного объема сплошных сред каждая точка (малая частица) в фиксированный момент (например, f = 0) имеет координаты x0, y0, z0 или другие параметры a, b, которые являются функцией этих координат Есть с «= F1 (* = 1)> r = r (a, b, c, / ). Рассмотренная ранее кинематика в одной точке использовала эту точечную лагранжеву переменную. Параметры a, b и c не использовались. Это потому, что нет другого смысла отличать проблемный момент.

Оставалась только временная зависимость координат точки или ее радиус-вектора. Для непрерывного носителя вы можете выбрать определенные точки, установив параметры a, b и c. Разные значения этих параметров соответствуют разным точкам на сплошной среде. Если движение непрерывной среды задается лагранжевыми переменными, скорость и ускорение этих переменных определяются обычными точечными кинематическими уравнениями. v = drfdt или vx = dx / dt; vf = dy / dt; vz = dz / dt; a = dv / dt == d2r / dt2, ax = d2x / 8t2; a ,, -d2y1d12; az-d2zl8t2. Производная по времени от i вычисляется для фиксированных значений переменных a, b и c, поэтому существует смещение.

Изменяя начальное условие бесконечно малым, а начальное вращение вокруг оси бесконечно близким к Оа0, породия превращается в небольшую замкнутую кривую, бесконечно близкую к вершинам малой оси. Людмила Фирмаль

Значения x, y, z или r также можно различить для каждой переменной a, b, c. В методе Лагранжа предметом исследования является точка движущихся сплошных сред. Переменная Эйлера. В механике сплошных сред, особенно в жидкостях и газах, а также в теории поля, в основном используются метод Эйлера и соответствующие переменные Эйлера. Метод Эйлера не учитывает точку пространства, занимаемую движущимися сплошными средами, а не неподвижные точки сплошных сред. Независимыми переменными являются время I и декартовы координаты точки M в пространстве x, y, z или другие параметры, которые характеризуют различные точки в пространстве.

Четыре независимые переменные x, y, z и t называются переменными Эйлера. Различные векторы и скалярные величины, характеризующие сплошные среды, такие как скорость и ускоритель Плотность считается функцией этих переменных. Для сплошных сред исследуются поля скалярных и векторных величин, характеризующих движущиеся сплошные среды, и их свойства. Изучите распределение этих величин в точке пространства, занятой сплошной средой, и изменение во времени. Из известного векторного поля скорости сплошной среды, заданного переменной Эйлера v = v (x, y, z, t), можно определить векторное поле ускорения a для этих переменных. Получите соответствующее выражение.

Переменное непрерывное движение среды Эйлера считается известным, если заданы поля скоростей этих переменных. Согласно определению ускорения точки сплошной среды в любой точке пространства A / (x, y, z) в момент времени t следует учитывать положение этой точки сплошной среды в момент времени t + Dm. В этой точке, благодаря движению сплошной среды, она находится в другой точке пространства Mt с координатами x + Dx, y + ky, z + Az и скоростью в соответствии с координатами этой новой точки в пространстве M и времени t + Dm.

Это становится. Поскольку изменение координат рассматриваемой точки сплошной среды в Дх, Ду, Дз произошло из-за изменения времени Д / lim l * m l * m X7 = Vl ‘(1) Увеличивает скорость r с помощью ряда степеней величин Dx, Dy, Dz, Dg. t> j = i> (x + Ax, y + Dy, z + Dz, f + D /) = d (x, y, z, r) ++ (dvldx) Ml & x + (dvldy) M ‘, & y + (Dvldz) M » & z + (dvldt) M ‘, & t + … Производные индексы M и t указывают, что они взяты в точке M (x, y, z) в пространстве в момент времени t. Согласно определению ускорения а точки сплошной среды в точке пространства М момента I, Остальные термины в серии исчезнут в определенных пределах.

• Подставляя (1) для (2) и для краткости, опуская индекс Миг производной. А = (dv / dt) + vx (dv / dx) + vf (dv / du) + vz (dv / dz) (3) В проекции на оси координат ax = dvx / 8t + vx (8vx / 8x) + vy (8 vx / 8y) + vt (8 vx / 8z); af = 8vy / 8t + vx (dvy / 8x) + vf (dvy / dy) + vz (8vy / dz);> (3 ‘) az = 8 vz / 5t + vx (5 vjdx) + vy (dvx / dy) + vz (8 vz / 8z). Используя векторное уравнение (3), если поле скорости известно, вычисляется поле переменного ускорения Эйлера. Эта формула включает группу dv / dt, которая является локальной производной вектора скорости, и vx (8vldx) + vy (dv / 8y) + + vz (8v / 8zj, конвекционная производная этого вектора).

Выражается во времени, т.е. ускорение, Dv / Dt. Локальная производная dv / dt характеризует изменение вектора скорости v в точке M (x, y, z) в пространстве вследствие одноразового изменения констант x, y, z. Полная производная от Dv / Dt равна локальной производной от dv / dt в точке пространства, где мгновенная скорость равна нулю. Группа членов, представляющих производную конвекции, учитывает изменение вектора скорости, вызванное движением точки рассмотрения сплошной среды самой движущейся средой.

Это положение равновесия считается устойчивым, если начальное отклонение стержня от положения равновесия достаточно мало. Людмила Фирмаль

Рассмотрим особые случаи. 1. Если v = v (x, y, z), т. Е. Поле скоростей стационарно, 8v / 8t = 0 и a = Dv / Dt = vx (dvldx + vAdvl8y + vz (8v / dz . 2. Когда v = vp, dv / 8x = 8v / dy = 8v / dz = 0 и a = Dv / Dt = dv / 8t. 3. Когда v = const, dv / 8t = O, dv / dx = dv / dy = ^ dv / dz = Q и a = Dv / Dt = 0. Уравнение (3) вычисляет полную или существенную производную по времени переменной Эйлера для любого вектора или скалярной величины, которая характеризует сплошную среду. Например, предположим, что известно поле скалярной плотности p (x, y, z, /) сплошной среды. Аргумент, аналогичный приведенному при выводе формулы ускорения, приводит к полной производной от p по времени t. Dp / Dt = 8p / dt + vx (5p / dx) + vy (8p / dd ‘) + vz (8p / dz).

Если сплошная среда не движется, то есть если ax = 1> y = r = 0, то согласно (3) полная производная по времени от векторной или скалярной функции, характеризующей сплошную среду, равна локальной производной. Преобразовав производную конвекции в (3), можно получить другое уравнение ускорения (формула Лэмба-Громекко). Где rotf — вектор скорости вихря, а V — символический оператор Гамильтона. i, J и A — единичные векторы, ориентированные вдоль декартовой оси координатных осей. Вихревая формула вектора скорости F j L £ d_ d Sx do cTz vx vy vz В будущем также будет использоваться вектор a>.

Это определяется как половина вектора скорости вихря. w = 1/2 r ° t «’ — (6) Проекция на координатные оси Чтобы прояснить физический смысл понятия rotv, рассмотрим несколько примеров расчета по заданному полю скорости. Пример 1. Непрерывная среда с постоянной скоростью оси Ox Векторная формула (5) _ Sv, Sv, _ _ Sv, Sv, Q ’= a7-a7 = O; = Q1 = g_ ^ = 0. Выполните плоское движение, параллельное v (рисунок 104). vx = o = const; in, = 0; существует «R = 0 и вихрь I = go1»: Рис. 104 Рисунок 105 Рисунок 106 Рис. 107 В результате fl = rotii = 0 в каждой точке пространства, занятого движущейся сплошной средой. Пример 2. Сплошная среда создает плоскую ось Ox со скоростью и распределением.

Параллельно (рисунок 105). Вот так. nxi + £ 1Д + Оск = Пример 3. Точка сплошной среды движется по круговой траектории, центр которой находится на оси Oz, а скорость которой обратно пропорциональна радиусу круга (рис. 106). То есть p = l / g, где n = const. У нас есть: -vsin 0) = 2в> о- В результате. A = go1b = 2

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

🔍 Видео

Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

Как решать уравнения с модулем или Математический торт с кремом (часть 1) | МатематикаСкачать

Решение биквадратных уравнений. 8 класс.Скачать

Уравнения Лагранжа второго родаСкачать

Уравнения Лагранжа второго рода. Задача 1Скачать

УРАВНЕНИЕ ОКРУЖНОСТИ. ЗАДАНИЕ 18 (С5). АРТУР ШАРИФОВСкачать

Уравнение Эйлера - bezbotvyСкачать

Основы вариационного исчисления | уравнение Эйлера Лагранжа | 1Скачать

№9. Элементы вариационного исчисления. Уравнения Лагранжа-Эйлера.Скачать

Билеты №32, 33 "Уравнения Максвелла"Скачать

Геометрический смысл производной. Уравнение касательнойСкачать

Уравнение состояния идеального газа. 10 класс.Скачать

Контрольная работа. Уравнения с МОДУЛЕМСкачать

Курс по ОДУ: Уравнения Клеро и Лагранжа | Занятие 8Скачать

Уравнение с модулемСкачать

Метод Лагранжа & Метод Бернулли ★ Решение линейных неоднородных дифференциальных уравненийСкачать

Алгебра 8 класс (Урок№19 - Уравнение х² = а.)Скачать