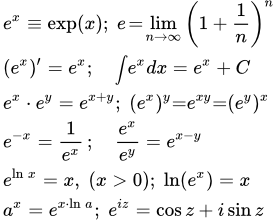В данной публикации мы рассмотрим, что такое экспонента, как выглядит ее график, приведем формулу, с помощью которой задается экспоненциальная функция, а также перечислим ее основные свойства.
- Определение и формула экспоненты
- График экспоненты
- Экспонента, е в степени х
- Определение
- Число e
- График экспоненты
- Формулы
- Частные значения
- Свойства экспоненты
- Область определения, множество значений
- Экстремумы, возрастание, убывание
- Обратная функция
- Производная экспоненты
- Интеграл
- Комплексные числа
- Выражения через гиперболические функции
- Выражения через тригонометрические функции
- Разложение в степенной ряд
- Что такое экспонента в математике для чайников
- Для чего используется экспонента?
- Экспоненциальный рост
- Что такое второй замечательный предел
- Как определить число е?
- Сумма ряда
- Формула Муавра — Стирлинга
- Как запомнить число е
- Интересные факты
- Число Непера и число Эйлера
- Число е – это не просто число
- Понятие экспоненциального роста
- Приглядимся поближе
Видео:Как решать дробно-рациональные уравнения? | МатематикаСкачать

Определение и формула экспоненты
Экспонента – это показательная функция, формула которой выглядит следующим образом:
Экспоненциальная функция (так часто называют экспоненту) может быть определена:
Через предел (lim):
Через степенной ряд Тейлора:
Видео:Что же это такое - ЧИСЛО Е и экспонента ??? Простым языком!)Скачать

График экспоненты
Ниже представлен график экспоненциальной функции
Как мы видим график (синяя линия) является выпуклым, строго возрастающим, т.е. при увеличении x увеличивается значение y .
Асимптотой является ось абсцисс, т.е. график во II четверти координатной плоскости стремится к оси Ox , но никогда не пересечет и не коснется ее.
Пересечение с осью ординат Oy – в точке , так как
Касательная (зеленая линия) к экспоненте проходит под углом 45 градусов в точке касания.
Видео:Функция ExpСкачать

Экспонента, е в степени х
Видео:Как решать уравнения с модулем или Математический торт с кремом (часть 1) | МатематикаСкачать

Определение
Экспоненту обозначают так , или .
Число e
Основанием степени экспоненты является число e . Это иррациональное число. Оно примерно равно
е ≈ 2,718281828459045.
Число e определяется через предел последовательности. Это, так называемый, второй замечательный предел:
.
Также число e можно представить в виде ряда:
.
Видео:Логарифм с нуля до уровня про. Уравнения, неравенства и параметр. Профильный ЕГЭСкачать

График экспоненты
На графике представлена экспонента, е в степени х.
y ( x ) = е х
На графике видно, что экспонента монотонно возрастает.
Видео:Решение тригонометрических уравнений. Подготовка к ЕГЭ | Математика TutorOnlineСкачать

Формулы
Основные формулы такие же, как и для показательной функции с основанием степени е .
Выражение показательной функции с произвольным основанием степени a через экспоненту:
.
Частные значения
Пусть y ( x ) = e x . Тогда
.
Видео:Определение exp(z). Формула Эйлера.Скачать

Свойства экспоненты
Экспонента обладает свойствами показательной функции с основанием степени е > 1 .
Область определения, множество значений
Экспонента y ( x ) = e x определена для всех x .
Ее область определения:
– ∞ .
Ее множество значений:
0 .
Экстремумы, возрастание, убывание
Экспонента является монотонно возрастающей функцией, поэтому экстремумов не имеет. Основные ее свойства представлены в таблице.
| y = е х | |
| Область определения | – ∞ |
| Область значений | 0 |
| Монотонность | монотонно возрастает |
| Нули, y = 0 | нет |
| Точки пересечения с осью ординат, x = 0 | y = 1 |
| + ∞ | |
| 0 |
Видео:✓ Число e на пальцах | Ботай со мной #054 | Борис Трушин |Скачать

Обратная функция
Видео:Трансцендентное (Логарифмическое) Уравнение из сборника олимпиадных задач Э.Н.БалаянаСкачать

Производная экспоненты
Производная е в степени х равна е в степени х:
.
Производная n-го порядка:
.
Вывод формул > > >
Видео:#40. ЛОГАРИФМИЧЕСКОЕ УРАВНЕНИЕ, ЗАДАНИЕ 13 ИЗ ПРОФИЛЬНОГО ЕГЭ ПО МАТЕМАТИКЕСкачать

Интеграл
Видео:Алгебра 7 Линейное уравнение с одной переменнойСкачать

Комплексные числа
Действия с комплексными числами осуществляются при помощи формулы Эйлера:
,
где есть мнимая единица:
.
Видео:Линейное уравнение с одним неизвестным.Скачать

Выражения через гиперболические функции
Видео:Логарифмы с нуля за 20 МИНУТ! Introduction to logarithms.Скачать

Выражения через тригонометрические функции
Видео:Решите уравнение ➜ ДВИ до ЕГЭСкачать

Разложение в степенной ряд
Использованная литература:
И.Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.
Автор: Олег Одинцов . Опубликовано: 25-02-2014 Изменено: 09-06-2018
Видео:1. Что такое дифференциальное уравнение?Скачать

Что такое экспонента в математике для чайников
Экспонента (экспоненциальная функция) — это математическая функция вида y = e×, или у = exp(x), или у = Exp(x) (где основанием степени является число е).
е — это число Эйлера, у него бесконечное количество цифр после запятой, оно трансцендентное и иррациональное. Оно равно округлённо 2,72 (а полностью — 2,718281828459045. ).
Трансцендентным число называется, если оно не удовлетворяет ни одному алгебраическому уравнению. Иррациональным — если его нельзя представить в виде дроби m/n, где n не равно 0.
Несмотря на свою бесконечность, число е является константой. То есть значением, которое никогда не изменяется.
Показательная функция — это математическая функция вида y = a×.
График экспоненты выглядит следующим образом:
Видео:Решение логарифмических уравнений #shortsСкачать

Для чего используется экспонента?
Экспонента применяется и в физике, и в технике, и в экономике, особенно при решении задач, связанных с процентами.
Видео:Уравнение касательной в точке. Практическая часть. 1ч. 10 класс.Скачать

Экспоненциальный рост
Мы используем термин экспоненциальный рост, чтобы сказать о стремительном росте чего-либо. Словосочетание чаще всего употребляется по отношению к росту популяции людей или животных/птиц.
Видео:Математический анализ. Алексей Савватеев и Александр Тонис. Лекция 13.4. Вычисление exp(i)Скачать

Что такое второй замечательный предел
Швейцарский математик Якоб Бернулли (1655–1705 гг.) вывел число е, когда пытался решить финансовый вопрос. В частности, он пытался понять, как должны начисляться проценты на сумму вклада в банке, чтобы это было наиболее прибыльно для владельца денег.
Он также пытался понять, есть ли лимит у дохода, получаемого в процентах, или он будет увеличиваться бесконечно.
Решая эту задачу, он использовал предел последовательности, а именно второй замечательный предел. Формулу для вычисления числа е можно записать следующим образом (где n — это число, стремящееся к бесконечности):
То есть числу е равняется предел, где n стремится к бесконечности, от 1, плюс 1, разделённый на n, и всё возвести в степень n.
Если подставить в данную формулу вместо n какую-нибудь очень большую цифру, можно получить очень хорошее приближение к е.
Например, подставим 1.000.000 и посчитаем на калькуляторе:
(1 + 1/1000000) ^ 1000000 = 2.7182804691
Как видите, с n = 1.000.000 мы получили достаточно хорошее приближение, с правильными 5 знаками после запятой.
Видео:Интеграл (1-x)*exp(-x)*ln(x)Скачать

Как определить число е?
Помимо второго замечательного предела, существуют и другие способы для определения числа е:
- через сумму ряда;
- через формулу Муавра — Стирлинга;
- другие.
Сумма ряда
Существует мнение, что этот метод использовал сам Эйлер, когда высчитывал е.
Можно получить приближение е, рассчитав первые 7 частей этой суммы:
И эти вычисления дали нам следующий результат:
Этот метод дал нам точных 4 знака после запятой, и его достаточно легко запомнить.
Формула Муавра — Стирлинга
Также называется просто формула Стирлинга:
И в этом случае чем больше n, тем точнее будет результат.
Видео:ЧТО ТАКОЕ МОДУЛЬ ЧИСЛА? #shorts #егэ #огэ #математика #профильныйегэСкачать

Как запомнить число е
Можно легко запомнить 9 знаков после запятой, если заметить удивительную закономерность: после «2,7» число «1828» появляется дважды (2,7 1828 1828). В 1828 году родились Лев Толстой и Жюль Верн, а Франц Шуберт умер.
Хотите дальше? Можно и дальше! 15 знаков после запятой! Последующие цифры — это градусы углов в равнобедренном прямоугольном треугольнике ( 45°, 90°, 45°): 2,7 1828 1828 45 90 45.
Интересные факты
Экспоненциальную функцию также называют экспонента.
Показательная функция — это функция вида y=a×, где a — заданное число (основание), x — это переменная.
А если основание = е, с переменной x, то математически логарифм записывается как ln, а не как log. И его называют натуральный логарифм (логарифм с основанием е):
Логарифмическая функция, что обратная к показательной функции y = a×, a > 0, a≠1, пишется как 
Производная и первообразная экспоненциальной функции равны ей самой, т. е. (e×)’ = e×, но (a×)’ = (a×)*ln(a).
Якобу Бернулли в расчётах помогал его брат Иоганн. Один из кратеров на Луне носит их имя.
Число Непера и число Эйлера
Число Непера или Неперово число, число Эйлера — это названия для одного и того же числа е.
Шотландский математик Джон Непер придумал логарифмы. Так как число е является основанием натурального логарифма (ln x), то этому числу присвоили имя математика из Шотландии. Хотя Непер и не вычислял его.
Сам символ e был придуман в 1731 году швейцарским математиком Леонардом Эйлером. Эйлер занимался вычислениями алгоритмов и вывел его основание. А точнее основание натурального логарифма, которым и является число е.
Изобретение логарифмов в XVII веке (1614 год) шотландским математиком Джоном Непером стало одним из важнейших событий в истории математики.
Узнайте также, что такое Число Пи и Логарифм.
Константу впервые вычислил швейцарский математик Якоб Бернулли в ходе решения задачи о предельной величине процентного дохода. Он обнаружил, что если исходная сумма $1 и начисляется 100% годовых один раз в конце года, то итоговая сумма будет $2. Но если те же самые проценты начислять два раза в год, то $1 умножается на 1,5 дважды, получая $2,25 (т. е. 1$*50%=1,5$, затем 1,5$*50%=2,25$). Начисления процентов раз в квартал (4 раза в год, т. е. каждый квартал к новой полученной сумме прибавляем 25%) получаем $2,44140625, и так далее. Бернулли показал, что если частоту начисления процентов бесконечно увеличивать, то процентный доход в случае сложного процента будет равен числу 2,718.
Число e всегда волновало меня — не как буква, а как математическая константа. Что число е означает на самом деле?
Разные математические книги и даже моя горячо любимая Википедия описывает эту величественную константу совершенно бестолковым научным жаргоном:
Математическая константа е является основанием натурального логарифма.
Если заинтересуетесь, что такое натуральный логарифм, найдете такое определение:
Натуральный логарифм, ранее известный как гиперболический логарифм, является логарифмом с основанием е, где е – иррациональная константа, приблизительно равная 2.718281828459.
Определения, конечно, правильные. Но понять их крайне сложно. Конечно, Википедия в этом не виновата: обычно математические пояснения сухи и формальны, составляются по всей строгости науки. Из-за этого новичкам сложно осваивать предмет (а когда-то каждый был новичком).
С меня хватит! Сегодня я делюсь своими высокоинтеллектуальными соображениями о том, что такое число е, и чем оно так круто! Отложите свои толстые, наводящие страх математические книжки в сторону!
Число е – это не просто число
Описывать е как «константу, приблизительно равную 2,71828…» — это все равно, что называть число пи «иррациональным числом, приблизительно равным 3,1415…». Несомненно, так и есть, но суть по-прежнему ускользает от нас.
Число пи — это соотношение длины окружности к диаметру, одинаковое для всех окружностей. Это фундаментальная пропорция, свойственная всем окружностям, а следовательно, она участвует в вычислении длины окружности, площади, объема и площади поверхности для кругов, сфер, цилиндров и т.д. Пи показывает, что все окружности связаны, не говоря уже о тригонометрических функциях, выводимых из окружностей (синус, косинус, тангенс).
Число е является базовым соотношением роста для всех непрерывно растущих процессов. Число е позволяет взять простой темп прироста (где разница видна только в конце года) и вычислить составляющие этого показателя, нормальный рост, при котором с каждой наносекундой (или даже быстрее) всё вырастает еще на немного.
Число е участвует как в системах с экспоненциальным, так и постоянным ростом: население, радиоактивный распад, подсчет процентов, и много-много других. Даже ступенчатые системы, которые не растут равномерно, можно аппроксимировать с помощью числа е.
Также, как любое число можно рассматривать в виде «масштабированной» версии 1 (базовой единицы), любую окружность можно рассматривать в виде «масштабированной» версии единичной окружности (с радиусом 1). И любой коэффициент роста может быть рассмотрен в виде «масштабированной» версии е («единичного» коэффициента роста).
Так что число е – это не случайное, взятое наугад число. Число е воплощает в себе идею, что все непрерывно растущие системы являются масштабированными версиями одного и того же показателя.
Понятие экспоненциального роста
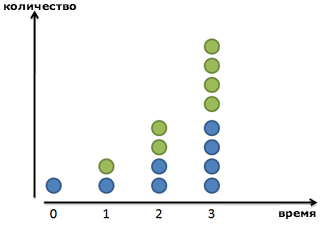
Давайте начнем с рассмотрения базовой системы, которая удваивается за определенный период времени. Например:
- Бактерии делятся и «удваиваются» в количестве каждые 24 часа
- Мы получаем вдвое больше лапшинок, если разламываем их пополам
- Ваши деньги каждый год увеличиваются вдвое, если вы получаете 100% прибыли (везунчик!)
И выглядит это примерно так:
Деление на два или удваивание – это очень простая прогрессия. Конечно, мы можем утроить или учетверить, но удваивание более удобно для пояснения.
Математически, если у нас есть х разделений, мы получаем в 2^x раз больше добра, чем было вначале. Если сделано только 1 разбиение, получаем в 2^1 раза больше. Если разбиений 4, у нас получится 2^4=16 частей. Общая формула выглядит так:
Другими словами, удвоение – это 100% рост. Мы можем переписать эту формулу так:
Это то же равенство, мы только разделили «2» на составные части, которыми в сущности и является это число: начальное значение (1) плюс 100%. Умно, да?
Конечно, мы можем подставить и любое другое число (50%, 25%, 200%) вместо 100% и получить формулу роста для этого нового коэффициента. Общая формула для х периодов временного ряда будет иметь вид:
Это просто означает, что мы используем норму возврата, (1 + прирост), «х» раз подряд.
Приглядимся поближе
Наша формула предполагает, что прирост происходит дискретными шагами. Наши бактерии ждут, ждут, а потом бац!, и в последнюю минуту они удваиваются в количестве. Наша прибыль по процентам от депозита магическим образом появляется ровно через 1 год. На основе формулы, написанной выше, прибыль растет ступенчато. Зеленые точки появляются внезапно.
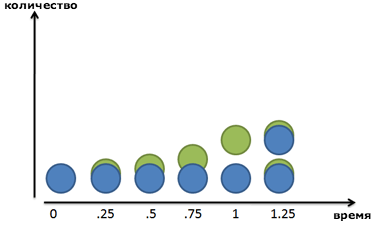
Но мир не всегда таков. Если мы увеличим картинку, мы увидим, что наши друзья-бактерии делятся постоянно:
Зеленый малый не возникает из ничего: он медленно вырастает из синего родителя. После 1 периода времени (24 часа в нашем случае), зеленый друг уже полностью созрел. Повзрослев, он стает полноценным синим членом стада и может создавать новые зеленые клеточки сам.
Эта информация как-то изменит наше уравнение?
Не-а. В случае с бактериями, полусформированные зеленые клетки все же не могут ничего делать, пока не вырастут и совсем не отделятся от своих синих родителей. Так что уравнение справедливо.