- Список вопросов теста
- Методы решения систем линейных алгебраических уравнений (СЛАУ) с примерами
- Методы решения систем линейных алгебраических уравнений (СЛАУ)
- Метод Крамера
- Матричный способ решения СЛАУ
- Метод Гаусса
- Ранг матрицы. Теорема Кронекера-Капелли
- Следствия из теоремы Кронекера — Капелли
- Методы Зейделя и простой итерации
- Методы решения систем линейных алгебраических уравнений
- Метод простых итераций
- Готовые работы на аналогичную тему
- Метод Зейделя
- Точные и приближенные методы решения систем линейных уравнений. Метод итераций
- 🎬 Видео
Видео:Решение системы линейных уравнений графическим методом. 7 класс.Скачать

Список вопросов теста
Вопрос 1
В чем выражается обычно относительная погрешность?
Варианты ответов
- В процентах (%)
- В процентах на единицу (%/ед.)
- В штуках (шт)
- В х (х)
Вопрос 2
Метод позволяющий получить корни системы с заданной точностью путем сходящихся бесконечных процессов
Варианты ответов
- точный метод
- итерационный метод
- метод Зейделя
- относительный метод
Вопрос 3
Этот метод является наиболее распространенным приемом решения систем линейных уравнений, алгоритм последовательного исключения неизвестных
Варианты ответов
- метод Гаусса
- метод обратный матриц
- аналитический метод
- ведущий метод
Вопрос 4
В чем заключается задача отделения корней?
Варианты ответов
- В установлении количества корней
- В установлении количества корней, а так же наиболее тесных промежутков, каждый из которых содержит только один корень.
- В установлении корня решения уравнения
- В назначении количества корней
Вопрос 5
К методам уточнения корней относится
Варианты ответов
- Метод дихотомии (метод половинного деления)
- Метод хорд
- Метод касательных
- Метод аппроксимации
Вопрос 6
Как иначе называют метод бисекций?
Варианты ответов
- Метод половинного деления
- Метод хорд
- Метод коллокации
- Метод пропорциональных частей
Вопрос 7
Отделение корней можно выполнить двумя способами:
Варианты ответов
- аналитическим и систематическим
- аналитическим и графическим.
- приближением и отделением
- систематическим и графическим
Вопрос 8
Суть комбинированного метода хорд и касательных?
Видео:Метод Крамера за 3 минуты. Решение системы линейных уравнений - bezbotvyСкачать

Методы решения систем линейных алгебраических уравнений (СЛАУ) с примерами
Содержание:
Видео:ПОСМОТРИ это видео, если хочешь решить систему линейных уравнений! Метод ПодстановкиСкачать

Методы решения систем линейных алгебраических уравнений (СЛАУ)
Метод Крамера
Определение: Системой линейных алгебраических уравнений (СЛАУ) называется выражение
Определение: Определитель, составленный из коэффициентов при неизвестных, называется главным определителем системы
Крамер предложил следующий метод решения СЛАУ: умножим главный определитель на 
Второй столбец умножим на 



Согласно записи СЛАУ первый столбец получившегося определителя представляет собой столбец свободных коэффициентов, т.е.
Определение: Определитель 
Поступая аналогично тому, как описано выше, найдем все вспомогательные определители СЛАУ:
31. Для того чтобы найти вспомогательный определитель i, надо в главном определителе СЛАУ заменить столбец i на столбец свободных коэффициентов.
Определение: Полученные выше соотношения называются формулами Крамера. Используя формулы Крамера, находят неизвестные величины 
- если главный определитель системы отличен от нуля (
), то система имеет единственное решение;
- если главный определитель системы равен нулю (
), а хотя бы один из вспомогательных определителей отличен от нуля (
или
, или, . или
), то система не имеет решений (деление на нуль запрещено);
- если все определители системы равны нулю (
), то система имеет бесчисленное множество решений.
Пример:
Решить СЛАУ методом Крамера
Решение:
Прежде всего, обращаем внимание на то, что в последнем уравнении переменные записаны в неправильном порядке, в этом случае говорят, что СЛАУ записана в ненормализованном виде. Нормализуем СЛАУ, для чего запишем неизвестные в последнем уравнении системы в правильном порядке, чтобы одноименные неизвестные были записаны друг под другом
Найдем главный определитель СЛАУ (раскрываем по первой строке)
Так как главный определитель системы отличен от нуля, то СЛАУ имеет единственное решение. Найдем три вспомогательных определителя
Воспользуемся формулами Крамера
Замечание: После нахождения решения СЛАУ надо обязательно провести проверку, для чего найденные числовые значения неизвестных подставляется в нормализованную систему линейных алгебраических уравнений.
Выполним проверку 
Матричный способ решения СЛАУ
Для решения СЛАУ матричным способом введем в рассмотрение матрицу, составленную из коэффициентов при неизвестных 

Тогда СЛАУ можно записать в матричном виде 





Пример:
Решить СЛАУ матричным способом
Решение:
Введем в рассмотрение следующие матрицы
Найдем матрицу 
Пример:
Решение:
Найдем алгебраические дополнения всех элементов 


Отсюда находим, что х = 1; y = l; z = l.
Метод Гаусса
Метод Гаусса или метод исключения неизвестных состоит в том, чтобы за счет элементарных преобразований привести СЛАУ к треугольному виду. Покажем использование расширенной матрицы, составленной из коэффициентов при неизвестных и расширенной за счет столбца свободных коэффициентов, для приведения СЛАУ к треугольному виду на примере системы, рассматриваемой в этой лекции. Расширенная матрица для СЛАУ имеет вид:
Замечание: В методе Гаусса желательно, чтобы первая строка расширенной матрицы начиналась с единицы.
Обменяем в расширенной матрице первую и вторую строки местами, получим 

Умножим элементы первой строки на (—1) и прибавим к соответствующим элементам третьей строки 

Из первого уравнения находим, что х = 1.
Вывод: Из вышеизложенного материала следует, что вне зависимости от
способа решения СЛАУ всегда должен получаться один и тот же ответ.
Замечание: После нахождения решения СЛАУ надо обязательно выполнить проверку, то есть подставить полученные значения неизвестных в заданную СЛАУ и убедиться в тождественности левой части всех равенств системы соответствующим правым частям. Отметим, что задание СЛАУ всегда верно, то есть, если проверка показывает нарушение оговоренной тождественности, то надо искать ошибку в проведенных вычислениях.
Ранг матрицы. Теорема Кронекера-Капелли
Определение: Рангом матрицы 
Если 
При вычислении ранга необходимо начинать вычислять миноры 2 порядка, затем миноры 3 порядка и так далее, пока не будут найдены миноры, обращающиеся в нуль. Если все миноры порядка p равны нулю, то и все миноры, порядок которых больше p, равны нулю.
Пример:
Найти ранг матрицы
Решение:
Очевидно, что среди миноров второго порядка есть миноры отличные от нуля, например, 


Теорема Кронекера-Капелли (критерий совместности СЛАУ). Для совместности системы линейных алгебраических уравнений (СЛАУ) необходимо и достаточно, чтобы ранг расширенной матрицы совпадал с рангом основной матрицы, составленной из коэффициентов при неизвестных величинах.
Видео:Математика без Ху!ни. Метод Гаусса.Скачать

Следствия из теоремы Кронекера — Капелли
Следствие: Если ранг матрицы совместной системы равен числу неизвестных, то система имеет единственное решение (то есть она определенная).
Следствие: Если ранг матрицы совместной системы меньше числа неизвестных, то система имеет бесчисленное множество решений (т.е. она неопределенная).
В случае неопределенной системы решения ищут следующим образом: выбираются главные неизвестные, число которых равно рангу, а остальные неизвестные считаются свободными; далее главные неизвестные выражаются через свободные и получают множество решений, зависящих от свободных неизвестных. Это множество решений называется общим решением системы. Придавая свободным неизвестным различные произвольные значения, получим бесчисленное множество решений, каждое из которых называется частным решением системы.
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Скалярное произведение и его свойства
- Векторное и смешанное произведения векторов
- Преобразования декартовой системы координат
- Бесконечно малые и бесконечно большие функции
- Критерий совместности Кронекера-Капелли
- Формулы Крамера
- Матричный метод
- Экстремум функции
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Telegram и логотип telegram являются товарными знаками корпорации Telegram FZ-LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Видео:Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Методы Зейделя и простой итерации
Вы будете перенаправлены на Автор24
Методы Зейделя и простой итерации — это методы решения систем линейных алгебраических уравнений при помощи итераций.
Видео:Решение системы линейных уравнений с двумя переменными способом подстановки. 6 класс.Скачать

Методы решения систем линейных алгебраических уравнений
Методы решения систем линейных алгебраических уравнений подразделяются на прямые, являющиеся точными, и итерационные, которые являются приближёнными. Прямые методы базируются на исполнении не бесконечного количества арифметических действий. В качестве примера таких методов можно привести метод обратной матрицы, метод Гаусса, метод Гаусса-Жордана, метод прогонки для трех диагональных матриц и так далее. Сущность итерационных методов состоит в том, чтобы путём последовательных приближений найти решение системы с требуемой точностью. Наиболее распространёнными итерационными методами считаются метод простых итераций и метод Зейделя. Они фактически являются эквивалентными, но конечно имеют и отличия.
Данные предполагают наличие больших расчетных объемов, однако это не мешает им обладать достаточно простой структурой. Как отмечалось выше, в итерационных методах за счет предыдущих приближений могут быть получены новые приближения, и, в случае удовлетворения системой условию сходимости, эти приближения имеют всё меньше отличий от аналитического решения.
В итерационных методах обычно присутствуют следующие основные этапы:
- Приведение исходной системы вида $ ¯A * ¯x = ¯b $ к итерационной форме.
- Осуществление проверки условия сходимости.
- Реализация решения системы выбранным методом.
Видео:Решение систем уравнений методом подстановкиСкачать

Метод простых итераций
Для систем общего вида должно выполняться тождество m = n, где m — это число уравнений в системе, а n — это количество неизвестных.
То есть, нет смысла в решении не доопределенных (m меньше n) и переопределенных (m больше n) систем уравнений, так как их можно свести за счёт элементарных алгебраических преобразований к нормальным (m=n) системам линейных уравнений. Иначе говоря, когда присутствует «ненормальная» система уравнений, то перед началом использования метода простых итераций, следует преобразовать её в нормальную.
Готовые работы на аналогичную тему
Систему линейных уравнений можно записать в матричной форме, где:
- A является матрицей коэффициентов.
- b является вектором свободных членов.
- x является вектором неизвестных.
В качестве примера рассмотрим следующую систему:
Рисунок 1. Система уравнений. Автор24 — интернет-биржа студенческих работ
Представим её в матричной форме:
Рисунок 2. Система уравнений в матричной форме. Автор24 — интернет-биржа студенческих работ
Первый этап итерационного метода заключается в преобразовании исходной системы, то есть матрицы А и вектора b в итерационную форму, где С и d являются итерационными формами исходных данных.
Преобразование в итерационный вид может быть реализована по следующим формулам:
$c_ = -a_ / a_$ $D_i = b_i / a_$ где i, j = 1,2,3…
Необходимо заметить, что диагональные компоненты новой матрицы обнуляются, хотя должны быть равны -1. В результате для рассматриваемой системы получается:
Рисунок 3. Матрица. Автор24 — интернет-биржа студенческих работ
Если выполнять преобразование исходной системы к итерационной форме, то она не удовлетворит условию сходимости:
Рисунок 4. Формула. Автор24 — интернет-биржа студенческих работ
То есть отдельные элементы матрицы C оказываются больше единицы. А по условию сходимости, приведённому выше, очевидно, что, если хотя бы один элемент будет больше единицы, то условие не выполнится, и решение системы путем простых итераций найти невозможно. Прежде чем осуществлять этапы итерационных методов, следует привести исходную систему к виду, в котором все диагональные компоненты будут максимальными по модулю в своих строках. Лишь при этом виде матрицы коэффициентов будет выполняться условие сходимости.
Очевидно, что в рассматриваемом примере третий элемент третьей строки по модулю больше других. Его следует оставить неизменным. Необходимо поменять местами первую и вторую строки, а далее умножить строку, ставшую первой, на минус единицу и сложить её с новой второй строкой. В результате получится:
Рисунок 5. Матрица. Автор24 — интернет-биржа студенческих работ
Теперь при подстановке в формулы итерационная форма получится верной и второй этап, то есть проверка условия сходимости, может быть успешно пройден. Если же система не проходит эту проверку, то приближения не будут сходиться к реальному решению, и ответ получен не будет. Если же условие сходимости исполняется, то стратегия метода простых итераций может быть применена и можно переходить к третьему этапу. В конечном счете будет получена система линейных алгебраических уравнений в итерационной форме:
Рисунок 6. Система линейных уравнений. Автор24 — интернет-биржа студенческих работ
Здесь $x_1, x_2, x_3$ являются приближениями, которые получаются на текущем шаге итерации за счет приближений, найденных на предыдущей итерации — $x^0_1, x^0_2, x^0_3$.
Итерационный процесс по методу простых итераций продолжается до тех пор, пока вектор приближений не придёт к необходимой точности, то есть, пока не исполнится условие выхода:
$Max|x_i – x^0_i|$ ∠ $ε$
Здесь ε является требуемой точностью.
Видео:Урок СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ С ДВУМЯ ПЕРЕМЕННЫМИ 7 КЛАСССкачать

Метод Зейделя
Как уже отмечалось выше, метод простых итераций и метод Зейделя, по своей сути, являются идентичными. Разница заключается в том, что в методе Зейделя вычисление вектора приближений на текущей итерации выполняется с применением данных, которые были получены ни только на предыдущей, но и на исполняемой итерации. Это означает, что элемент x1 определяется через x2 и x3, величины которых были рассчитаны на предыдущей итерации, а последующий элемент x2 уже рассчитывается на основании x1, найденного именно на текущей итерации, и x3, вычисленного на предыдущей. Иначе говоря, данные в методе Зейделя для определения вектора X используются в процессе расчётов по мере их вычисления. А в методе простых итераций применяются данные, которые были получены именно на предыдущей итерации.
На основании этого отличия можно сделать вывод о том, что метод Зейделя имеет лучшую сходимость в сравнении с методом простых итераций, поскольку для него характерна тенденция применения приближений, которые получаются по ходу процесса и являются наиболее близкими к конечному результату.
Ниже представлена программная реализация метода Зейделя:
Procedure Zeidel(C:array of array of real;d:array of real;n:integer);
Видео:15. Однородная система линейных уравнений / фундаментальная система решенийСкачать

Точные и приближенные методы решения систем линейных уравнений. Метод итераций
Численный метод решения задачи называется точным, если при точном выполнении всех требуемых действий мы получаем точное решение системы. При этом имеется в виду, что все коэффициенты, данные и параметры задачи представляют собой точные значения. Заметим, что методы Гаусса и Жордана — Гаусса, основанные на процессе исключения неизвестных, являются точными.
Если же в результате точного выполнения всех требуемых действий и точном значении всех входящих в условие задачи данных, коэффициентов и параметров получается приближенный результат, то метод называется приближенным. Все рассмотренные в гл. 2 численные методы нахождения корней уравнения являются приближенными.
В случае применения приближенного метода, помимо погрешностей данных, коэффициентов и параметров задачи и погрешностей округления в промежуточных действиях, на окончательный результат всегда влияет и погрешность самого метода.
К числу приближенных методов относится и метод итераций, применимый и к решению систем линейных уравнений. Несмотря на то что данный метод является приближенным, он обладает такими качествами, которые делают его весьма выгодным с вычислительной точки зрения.
Далее кратко рассмотрим метод итераций (к слову, он гораздо проще реализуется в среде Microsoft Excel, чем метод Жордана — Гаусса). Сущность метода изложим на примере системы трех линейных уравнений с тремя неизвестными.
Пусть дана система трех линейных уравнений с тремя неизвестными. Для применения метода итераций приведем систему к виду
Систему вида (3.14) будем называть системой нормального вида. Пусть (х0; j0; z0) есть некоторое грубо приближенное решение системы. Назовем эту совокупность чисел начальным приближением. Если какое-либо грубое приближение неизвестно, то за него можно взять вообще произвольную совокупность значений неизвестных и принять его за начальное приближение. Часто за начальное приближение берут совокупность свободных членов: (Dp, Dp, D3). Подставим числа х0, у0, 2 о в правые части системы (3.14). В левых частях системы (3.14) получаем некоторые значения переменных х, у, z. Обозначим иххьуь zx и назовем первым приближением. Подставив числа х1; уг, zx в правые части системы (3.14), получим второе приближение: х2, y2, z2. Этот процесс можно осуществлять неограниченно. При некоторых условиях, налагаемых на коэффициенты Аь В ь Ci,A2,. С3, к-е приближение хк, ук, zk при возрастании к будет становиться сколь угодно близким к истинному решению системы (х; у*; z»).
Мы говорим в этом случае, что итерационный процесс сходится. Значит, проведя процесс достаточно большое число раз, мы получим приближенное решение системы.
Заметим, что систему (3.14) и аналогичные системы п линейных уравнений с п неизвестными можно записать в матричном виде. Обозначим
Тогда систему (3.14) и аналогичные ей системы п линейных уравнений с п неизвестными можно записать так:
Сформулируем теперь достаточные условия сходимости итерационного процесса.
Достаточные условия сходимости итерационного процесса:
- 1. Сумма модулей элементов каждой строки матрицы А (сумма модулей коэффициентов каждого уравнения системы (3.14)) меньше единицы.
- 2. Сумма квадратов всех элементов каждой строки матрицы А (сумма квадратов коэффициентов каждого уравнения системы (3.14)) меньше единицы.
Найдите решение системы линейных алгебраических уравнений
методом итераций с точностью до 10 -7 .
Найдем сумму модулей коэффициентов при неизвестных в каждом уравнении.
В первом уравнении: 0,12 + 0,18 + 0,08 = 0,38.
Во втором уравнении: 0,15 + 0,06 + 0,11 = 0,32.
В третьем уравнении: 0,04 + 0,10 + 0,09 = 0,23.
Для каждого из уравнений эта сумма меньше единицы, значит, итерационный процесс сходится, и мы можем получить приближенное решение системы методом итераций. Откроем файл «Численные методы линейной алгебры» (Microsoft Excel). Переименуем лист 3 в лист «Метод итераций». Объединим ячейки А1—F1 и поместим туда надпись Начальное приближение. Объединим ячейки Gl—II и поместим туда надпись Матрица системы. В ячейку Л поместим надпись Свободные члены. В ячейки диапазона G2—14 поместим матрицу Л системы, а в ячейки диапазона J2—J4 — свободные члены системы. В ячейку А2 поместим х0=, в ячейку С2 поместим у0=, в ячейку F2 поместим z0=. В ячейки В2, D2 и F2 поместим начальные приближения решения, равные свободным членам системы: -0,64; 0,26; 1,34 соответственно.
Теперь в ячейку АЗ поместим х1=, в ячейку СЗ поместим у1=, в ячейку F3 поместим zl=. В ячейку ВЗ поместим формулу =$G$2*B2+$H$2*D2+$I$2*F2+$J$2 , в ячейку D3 поместим формулу
=$G$3*B2+$H$3*D2+$I$3*F2+$J$31, а в ячейку F3 — формулу
Рис. ЗА. Решение систем линейных уравнений методом итераций
| =$G$4*B2+$H$4*D2+$I$4*F2+$J$4 1. Скопируем ячейки диапазона A3—F3 и последовательно вставляем их вниз до тех пор, пока два соседних значения в каждом из столбцов не станут равными. Эти значения и будут нужными приближениями. Исправляем нумерацию индексов в нужных ячейках столбцов А, С и Е и получаем значения (рис. 3.4):
Округляя полученные значения до семи знаков после запятой, получаем приближенное решение задачи: х
🎬 Видео
Решение системы уравнений методом ГауссаСкачать

Матричный метод решения систем уравненийСкачать

Общее, частное, базисное решение системы линейных уравнений Метод ГауссаСкачать

Как ЛЕГКО РЕШАТЬ Систему Линейный Уравнений — Метод СложенияСкачать

Система линейных уравнений. Общее решение. Метод ГауссаСкачать

9 класс, 11 урок, Методы решения систем уравненийСкачать

метод Гаусса СИСТЕМА ЛИНЕЙНЫХ УРАВНЕНИЙ решение СЛАУСкачать

12. Метод Гаусса решения систем линейных уравнений. Часть 1.Скачать

МЕТОД ГАУССА 😉 #егэ #математика #профильныйегэ #shorts #огэСкачать

Математика без Ху!ни. Метод Гаусса. Совместность системы. Ранг матрицы.Скачать

Метод Гаусса решения систем линейных уравненийСкачать







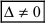 ), то система имеет единственное решение;
), то система имеет единственное решение;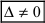 ), а хотя бы один из вспомогательных определителей отличен от нуля (
), а хотя бы один из вспомогательных определителей отличен от нуля ( 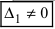 или
или 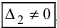 , или, . или
, или, . или 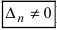 ), то система не имеет решений (деление на нуль запрещено);
), то система не имеет решений (деление на нуль запрещено);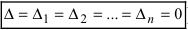 ), то система имеет бесчисленное множество решений.
), то система имеет бесчисленное множество решений.
























