Этот человек французский математик он придумал теорию уравнений и изобрел координаты кто это

Видео:Математика это не ИсламСкачать

Возникновение системы координат

Система координат – гениальное изобретения человеческого ума. Начало было положено ученым Гиппархом, предложившим ввести географическое координаты.

Намного позднее в17 веке французский математик Рене Декарт систематизировал научные знания и тем самым стал основоположником на данный момент самой известной и применяемой системой координат – ортонормированной.

Видео:Когнитивная наука как конвергентное знание. Татьяна ЧерниговскаяСкачать

Рене Декарт и его система

Фундаментальные идеи Декарта были изложены в книге «Геометрия». Впервые Декарт применил в геометрии алгебраические методы. Именно в этой книге он ввел понятие прямоугольная система координат.

Видео:Человек, который познал бесконечность / Фильм о выдающемся математике .Скачать

Примеры прямоугольных систем координат

• система координат на плоскости;
• система координат в пространстве.

Декартова система координат включает в себя две взаимно перпендикулярные оси координат.

Для каждой из которых выбрано определенное направление на плоскости или в пространстве и пересекаются они в точке, обозначаемой как начало координат.

Видео:Студенты российского вуза разработали вечный двигатель #вечныйдвигатель #изобретенияСкачать

Рене Декарт

Фото Все

Видео Все

Рене Декарт — Фильм из цикла «Философы» («Filosofos»)

Декарт философия кратко

Андрей Гасилин: «Рационализм Рене Декарта»

Видео:Разочарование в стероидахСкачать

Рене Декарт — биография

Рене Декарт – философ, механик, математик, физик, физиолог, создавший аналитическую геометрию и современную алгебраическую символику.

Cogito, ergo sum – я мыслю, следовательно, я существую. Эта фраза сделала бессмертным Рене Декарта. После него осталось огромное наследие, причем в абсолютно разных отраслях науки, ему принадлежит открытие алгебраической символики, применяемой и сейчас, он оставил свой след в геометрии, физике и рефлексологии, но именно эта фраза содержит главную философскую идею, которой он придерживался всю жизнь.

Детство

Родился Рене Декарт 31 марта 1596 года в городе Лаэ, провинция Турень. Сейчас этот город носит его имя. Отец мальчика – Иоахим Декарт, принадлежал к обедневшему дворянскому роду. Он состоял в парламенте, занимал должность судьи бретонского Высшего суда городка Ренн. Дома он бывал только шесть месяцев в году, остальное время находился на службе. Мама Рене – Жанна Брошар, дочь наместника короля в провинции.

Рене был самым младшим из трех сыновей. Мама умерла, когда он был годовалым малышом, поэтому воспитанием всех трех детей занималась бабушка по материнской линии.

С раннего детства мальчик отличался повышенной любознательностью и пытливым умом, но физически он был очень слаб. Первым учебным заведением Рене стала иезуитская коллегия Ла Флеш. Все ученики подчинялись строгим правилам этого учреждения, и только для Декарта делали некоторые поблажки. Например, ему разрешали подольше поспать, в отличие от других учеников.

Портрет Рене Декарта

Образовательный процесс в этом заведении строился на религиозной направленности, впрочем, как и во всех ему подобных. Рене стремился к знаниям, он дорожил учебой, но вскоре он начал сомневаться в искренности философских авторитетов.

После завершения учебы в коллегии, молодой человек уехал в Пуатье, где продолжил обучение в области права и спустя некоторое время стал бакалавром. Потом юноша недолго живет в столице, в 1617-м записывается в армию. Он сражался в Голландии, где в те годы бушевала революция, потом их часть перебросили в Прагу. Во время пребывания в Голландии, состоялась встреча Декарта и физика Исаака Бекмана.

Затем молодой человек возвращается в Париж, выдвигает свои революционные идеи, так не понравившиеся иезуитам. Опасаясь их преследования, Рене уехал в Голландию, откуда не выезжал на протяжении двадцати лет. Всю свою жизнь Декарт страдал от гонений и нападок церкви, которая отвергала его прогрессивные идеи, никак не соответствующие уровню развития тогдашней науки.

Философия

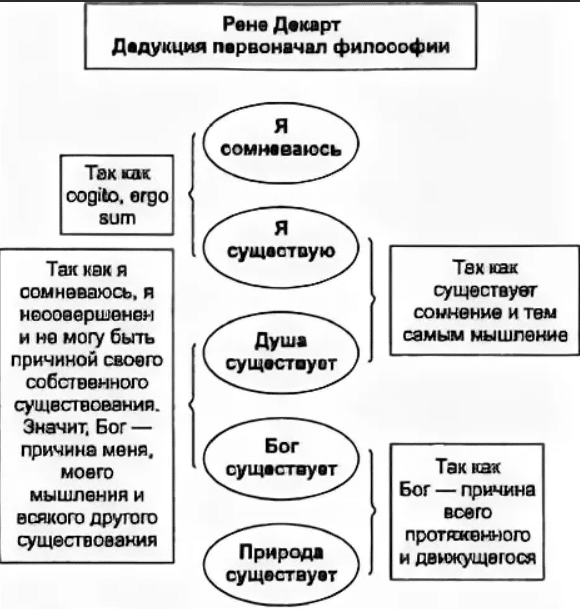
В философских изысканиях Рене Декарт придерживался дуализма – он верил в существование двух субстанций: материальной и идеальной. Каждое из этих начал он считал самостоятельным. Помимо этого он придерживался концепции, что в мире существуют два вида сущностей – мыслящие и протяженные, и что обе они сформированы Богом. Для формирования их, Бог использует одинаковые законы, материя создается одновременно с движением, покоем и сохранением субстанций.

Одним из универсальных методов познания Декарт считал рационализм. Ученый придерживался мнения, что человек является господствующей силой над природой. Рене считал, что именно несовершенство человека и его непохожесть на Бога сковывает возможности его разума. Эти рассуждения Декарта впоследствии стали основой для закладки рационализма.

Ученый исходил из того, что нельзя считать общепризнанные знания и суждения правдивыми и безошибочными, он призывал сомневаться во всем. Известная фраза «Я мыслю – следовательно, я существую» вызвана именно этими сомнениями.

По мнению философа, каждый может усомниться в существовании не только собственной телесной оболочки, но и окружающего его мира в целом. Однако сомнение от этого никуда не денется.

Видео:СУРДИН и САВВАТЕЕВ: Неземные математики / Плоская Земля / Математика и война. Неземной подкастСкачать

Секреты мира

Видео:Алексей Савватеев против мифов о математике // Наука противСкачать

Все открытия впереди!

Видео:Уравнение, которое меняет взгляд на мир [Veritasium]Скачать

Кто изобрел оси координат

Видео:Оператор набла (оператор Гамильтона) и оператор ЛапласаСкачать

Кто придумал систему координат?

Система координат – гениальное изобретения человеческого ума. Начало было положено ученым Гиппархом, предложившим ввести географическое координаты.

Намного позднее в17 веке французский математик Рене Декарт систематизировал научные знания и тем самым стал основоположником на данный момент самой известной и применяемой системой координат – ортонормированной.

Рене Декарт и его система

Фундаментальные идеи Декарта были изложены в книге «Геометрия». Впервые Декарт применил в геометрии алгебраические методы. Именно в этой книге он ввел понятие прямоугольная система координат.

Примеры прямоугольных систем координат

• система координат на плоскости;
• система координат в пространстве.

Декартова система координат включает в себя две взаимно перпендикулярные оси координат.

Для каждой из которых выбрано определенное направление на плоскости или в пространстве и пересекаются они в точке, обозначаемой как начало координат.

Видео:Теория струн. Темная материя и Теория почти всего.Скачать

История возникновения координат на плоскости

История возникновения координат на плоскости

История возникновения координат и системы координат начинается очень давно, первоначально идея метода координат возникла ещё в древнем мире в связи с потребностями астрономии, географии, живописи. Древнегреческого ученого Анаксимандра Милетского (ок. 610-546 до н. э.) считают составителем первой географической карты. Он четко описывал широту и долготу места, используя прямоугольные проекции.

Более чем за 100 лет до н.э греческий ученый Гиппарх предложил опоясать на карте земной шар параллелями и меридианами и ввести теперь хорошо известные географические координаты: широту и долготу и обозначить их числами.

Идея изображать числа в виде точек, а точкам давать числовые обозначения зародилась в далекой древности. Первоначальное применение координат связано с астрономией и географией, с потребностью определять положение светил на небе и определенных пунктов на поверхности Земли, при составлении календаря, звездных и географических карт. Следы применения идеи прямоугольных координат в виде квадратной сетки (палетки) изображены на стене одной из погребальных камер Древнего Египта.

Основная заслуга в создании современного метода координат принадлежит французскому математику Рене Декарту. До наших времён дошла такая история, которая подтолкнула его к открытию. Занимая в театре места, согласно купленным билетам, мы даже не подозреваем, кто и когда предложил ставший обычным в нашей жизни метод нумерации кресел по рядам и местам. Оказывается эта идея осенила знаменитого философа, математика и естествоиспытателя Рене Декарта (1596-1650)– того самого, чьим именем названы прямоугольные координаты. Посещая парижские театры, он не уставал удивляться путанице, перебранкам, а подчас и вызовам на дуэль, вызываемыми отсутствием элементарного порядка распределения публики в зрительном зале. Предложенная им система нумерации, в которой каждое место получало номер ряда и порядковый номер от края, сразу сняла все поводы для раздоров и произвела настоящий фурор в парижском высшем обществе.

Научное описание прямоугольной системы координат Рене Декарт впервые сделал в своей работе «Рассуждение о методе» в 1637 году. Поэтому прямоугольную систему координат называют также — Декартова система координат. Кроме того, в своей работе «Геометрия» (1637), открывшей взаимопроникновение алгебры и геометрии, Декарт ввел впервые понятия переменной величины и функции. «Геометрия» оказала огромное влияние на развитие математики. В декартовой системе координат получили реальное истолкование отрицательные числа.

Кроме математики интересы Декарта распространялись на физику, где он дал четкую формулировку закона инерции, открыл закон преломления световых лучей на границе двух различных сред («Диоптрика», 1637).

Вклад в развитие координатного метода внес также Пьер Ферма, однако его работы были впервые опубликованы уже после его смерти. Декарт и Ферма применяли координатный метод только на плоскости. Координатный метод для трёхмерного пространства впервые применил Леонард Эйлер уже в XVIII веке.

Видео:Самая простая нерешённая задача — гипотеза Коллатца [Veritasium]Скачать

Система координат — это. Что такое Система координат?

Система координат — комплекс определений, реализующий метод координат, то есть способ определять положение точки или тела с помощью чисел или других символов. Совокупность чисел, определяющих положение конкретной точки, называется координатами этой точки.

В математике координаты — совокупность чисел, сопоставленных точкам многообразия в некоторой карте определённого атласа.

В элементарной геометрии координаты — величины, определяющие положение точки на плоскости и в пространстве. На плоскости положение точки чаще всего определяется расстояниями от двух прямых (координатных осей), пересекающихся в одной точке (начале координат) под прямым углом; одна из координат называется ординатой, а другая — абсциссой. В пространстве по системе Декарта положение точки определяется расстояниями от трёх плоскостей координат, пересекающихся в одной точке под прямыми углами друг к другу, или сферическими координатами, где начало координат находится в центре сферы.

В географии координаты — широта, долгота и высота над известным общим уровнем (например, океана). См. географические координаты.

В астрономии координаты — величины, при помощи которых определяется положение звезды, например, прямое восхождение и склонение.

Небесные координаты — числа, с помощью которых определяют положение светил и вспомогательных точек на небесной сфере. В астрономии употребляют различные системы небесных координат. Каждая из них по существу представляет собой систему полярных координат на сфере с соответствующим образом выбранным полюсом. Систему небесных координат задают большим кругом небесной сферы (или его полюсом, отстоящим на 90° от любой точки этого круга) с указанием на нём начальной точки отсчёта одной из координат. В зависимости от выбора этого круга системы небесных координат называлась горизонтальной, экваториальной, эклиптической и галактической.

Наиболее используемая система координат — прямоугольная система координат (также известная как декартова система координат).

Координаты на плоскости и в пространстве можно вводить бесконечным числом разных способов. Решая ту или иную математическую или физическую задачу методом координат, можно использовать различные координатные системы, выбирая ту из них, в которой задача решается проще или удобнее в данном конкретном случае. Известным обобщением системы координат являются системы отсчёта и системы референции.

Список наиболее распространённых систем координат

Основные системы

В этом разделе даются разъяснения к наиболее употребляемым системам координат в элементарной математике.

Декартовы координаты

Основная статья: Прямоугольная система координат

Расположение точки P на плоскости определяется декартовыми координатами с помощью пары чисел :

• — расстояние от точки P до оси y с учетом знака
• — расстояние от точки P до оси x с учетом знака

В пространстве же необходимо уже 3 координаты :

• — расстояние от точки P до плоскости yz
• — расстояние от точки P до плоскости xz
• — расстояние от точки P до плоскости xy

Полярные координаты

Основная статья: Полярная система координат

В полярной системе координат положение точки определяется расстояние до центра координат и углом радиус-вектора с осью Ox.

Термин «полярные координаты» используется только на плоскости, в пространстве применяются цилиндрические и сферические системы координат.

Цилиндрические координаты

Основная статья: Цилиндрическая система координат

Цилиндрические координаты — трехмерный аналог полярных, в котором точка P представляется трехкомпонентным кортежем . В терминах декартовой системы координат,

• (радиус) — расстояние от оси z к точке P,
• (азимут или долгота) — угол между положительной («плюсовой») частью оси x и прямой линии, мысленно проведённой от полюса до точки P, спроектирован на xy-плоскость
• (высота) — расстояние (с учетом знака) от xy-плоскости до точки P.

Примечание: в литературе можно встретить пометку z для h; это не принципиально, но нужно следить, какие отметки применяются.

Полярные координаты имеют один недостаток: значение θ теряет смысл, если r = 0.

Цилиндрические координаты полезны для изучения систем, симметричных вокруг некой оси. Например, длинный цилиндр в декартовых координатах имеет уравнение , тогда как в цилиндрических оно выглядит как r = c

Сферические координаты

Основная статья: Сферическая система координат

Сферические координаты — трехмерный аналог полярных

Обозначения, принятые в Америке

В сферической системе координат, расположение точки P определяется тремя компонентами: . В терминах декартовой системы координат,

• (радиус) — это расстояние от точки Р до полюса,
• (широта или полярный угол) — угол между z-осью и прямой, проведённой из полюса до точки P
• (азимут или долгота) — угол между положительной («плюсовой» x-осью и проекцией прямой, проведённой из полюса до точки P на xy-плоскость.

Примечание: в литературе можно встретить пометку φ или θ, а также r для ρ;

Сферическая система координат также имеет недостаток: φ теряет смысл если ρ = 0, также и θ теряет смысл, если ρ = 0 или φ = 0 или φ = 180°.

Для построения точки по её сферическими координатами, нужно: от полюса отложить отрезок, равный ρ вдоль положительной z-оси, вернуть его на угол φ вокруг оси y в направлении положительной x-оси, и вернуть на угол θ вокруг z-оси в направлении положительной y-оси.

Сферические координаты полезны при изучении систем, симметричных вокруг точки. Так, уравнение сферы в декартовых координатах выглядит как , тогда как в сферических становится намного проще: .

Европейские обозначения

В Европе принято использовать другие обозначения. Положение точки задаётся числами: , Где r — расстояние от точки до начала координат, — полярный угол, который изменяется в пределах от 0 до π, — Азимутальный угол, который изменяется в пределах от 0 до 2π. То есть, в европейской системе, которая применяется также и в России, обозначения для углов переставлены по сравнению с американской.

Переход из одной системы координат в другую

Декартовы и полярные

где u0 — функция Хевисайда с , а sgn — функция signum . Здесь функции u0 и sgn используются как «логические» переключатели, аналогичные по значению операторам «если .. то» (if…else) в языках программирования. Некоторые языки программирования имеют специальную функцию atan2 (y, x), которая находит правильный θ в необходимом квадранте, определённом x и y.

Декартовы и цилиндрические

Декартовы и сферические

Уравнения для американских обозначений

Цилиндрические и сферические

См. также

Литература

• Гельфанд И. М., Глаголева Е. Г., Кириллов А. А. Метод координат. Издание пятое, стереотипное. Серия: Библиотечка физико-математической школы. Математика. Выпуск 1. М.: Наука, 1973.

Ссылки

• Факультативное занятие по математике на тему: «Разные системы координат»

Видео:Переставь одну цифру! Задача на логикуСкачать

Декартова система координат — это. Что такое Декартова система координат?

Прямоугольная, или декартова система координат — наиболее распространённая система координат на плоскости и в пространстве.

Прямоугольная система координат на плоскости

Прямоугольная система координат на плоскости образуется двумя взаимно перпендикулярными осями координат X’X и Y’Y. Оси координат пересекаются в точке O, которая называется началом координат, на каждой оси выбрано положительное направление.Положительное направление осей (в правосторонней системе координат) выбирают так, чтобы при повороте оси X’X против часовой стрелки на 90° её положительное направление совпало с положительным направлением оси Y’Y. Четыре угла (I, II, III, IV), образованные осями координат X’X и Y’Y, называются координатными углами (см. Рис. 1).

Положение точки A на плоскости определяется двумя координатами x и y. Координата x равна длине отрезка OB, координата y — длине отрезка OC в выбранных единицах измерения. Отрезки OB и OC определяются линиями, проведёнными из точки A параллельно осям Y’Y и X’X соответственно. Координата x называется абсциссой точки A, координата y — ординатой точки A. Записывают так: A(x, y).

Если точка A лежит в координатном угле I, то точка A имеет положительные абсциссу и ординату. Если точка A лежит в координатном угле II, то точка A имеет отрицательную абсциссу и положительную ординату. Если точка A лежит в координатном угле III, то точка A имеет отрицательные абсциссу и ординату. Если точка A лежит в координатном угле IV, то точка A имеет положительную абсциссу и отрицательную ординату.

Прямоугольная система координат в пространстве

Прямоугольная система координат в пространстве образуется тремя взаимно перпендикулярными осями координат OX, OY и OZ. Оси координат пересекаются в точке O, которая называется началом координат, на каждой оси выбрано положительное направление, указанное стрелками, и единица измерения отрезков на осях. Единицы измерения одинаковы для всех осей. OX — ось абсцисс, OY — ось ординат, OZ — ось апликат. Положительное направление осей выбирают так, чтобы при повороте оси OX против часовой стрелки на 90° её положительное направление совпало с положительным направлением оси OY, если этот поворот наблюдать со стороны положительного направления оси OZ. Такая система координат называется правой. Если большой палец правой руки принять за направление X, указательный за направление Y, а средний за направление Z, то образуется правая система координат. Аналогичными пальцами левой руки образуется левая система координат. Правую и левую системы координат невозможно совместить так, чтобы совпали соответствующие оси (см. Рис. 2).

Положение точки A в пространстве определяется тремя координатами x, y и z. Координата x равна длине отрезка OB, координата y — длине отрезка OC, координата z — длине отрезка OD в выбранных единицах измерения. Отрезки OB, OC и OD определяются плоскостями, проведёнными из точки A параллельно плоскостям YOZ, XOZ и XOY соответственно. Координата x называется абсциссой точки A, координата y — ординатой точки A, координата z — аппликатой точки A. Записывают так: A(a, b, c).

Прямоугольная система координат (любой размерности) также описывается набором ортов, сонаправленных с осями координат. Количество ортов равно размерности системы координат и все они перпендикулярны друг другу.

В трёхмерном случае такие орты обычно обозначаются i j k или ex ey ez . При этом в случае правой системы координат действительны следующие формулы с векторным произведением векторов:

История

Впервые прямоугольную систему координат ввел Рене Декарт в своей работе «Рассуждение о методе» в 1637 году. Поэтому прямоугольную систему координат называют также — Декартова система координат. Координатный метод описания геометрических объектов положил начало аналитической геометрии. Вклад в развитие координатного метода внес также Пьер Ферма, однако его работы были впервые опубликованы уже после его смерти. Декарт и Ферма применяли координатный метод только на плоскости.

Координатный метод для трёхмерного пространства впервые применил Леонард Эйлер уже в XVIII веке.

🔥 Видео

Алексей Савватеев. Политика, математика и Бог.Скачать

Почему существует Вселенная | ALIСкачать

Почему простые числа образуют спирали? [3Blue1Brown]Скачать

Та самая девочка в твоём классе 🤮😍 #shortsСкачать

Лекция Алексея Семихатова «Жизнь после Хиггса».Скачать

Олег Тиньков тогда и сейчас, с приходом успеха.Скачать

👽Он хочет выглядеть как пришелец. Black Alien ProjectСкачать

ТЕХНИКА БЕЗОПАСНОСТИ. Вид Грубейшего Нарушения ТРЕБОВАНИЙ ТБ при работе на СТАНКАХ.Скачать