- Основные понятия о линейных дифференциальных уравнениях второго порядка и их решениях
- Линейное однородное дифференциальное уравнение второго порядка и его решение
- Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами: теория и практика
- Решить линейное однородное дифференциальное уравнение с постоянными коэффициентами самостоятельно, а затем посмотреть решение
- Если y1 и y2 два линейно независимых решения дифференциального уравнения
- Линейные дифференциальные уравнения второго порядка.
- 💡 Видео
Видео:Линейное неоднородное дифференциальное уравнение с постоянными коэффициентами 4y''-y=x^3-24x #1Скачать

Основные понятия о линейных дифференциальных уравнениях второго порядка и их решениях
Линейным дифференциальным уравнением второго порядка называется уравнение вида
где y — функция, которую требуется найти, а p(x) , q(x) и f(x) — непрерывные функции на некотором интервале (a, b) .
Если правая часть уравнения равна нулю ( f(x) = 0 ), то уравнение называется линейным однородным уравнением. Таким уравнениям и будет в основном посвящена практическая часть этого урока. Если же правая часть уравнения не равна нулю ( f(x) ≠ 0 ), то уравнение называется линейным неоднородным уравнением (смотрите отдельный урок).
В задачах от нас требуется разрешить уравнение относительно y» :
Линейные дифференциальные уравнения второго порядка имеют единственное решение задачи Коши.
Видео:Задача Коши ➜ Частное решение линейного однородного дифференциального уравненияСкачать

Линейное однородное дифференциальное уравнение второго порядка и его решение
Рассмотрим линейное однородное дифференциальное уравнение второго порядка:
Если y 1 (x) и y 2 (x) — частные решения этого уравнения, то верны следующие высказывания:
1) y 1 (x) + y 2 (x) — также является решением этого уравнения;
2) Cy 1 (x) , где C — произвольная постоянная (константа), также является решением этого уравнения.
Из этих двух высказываний следует, что функция
также является решением этого уравнения.
Возникает справедливый вопрос: не является ли это решение общим решением линейного однородного дифференциального уравнения второго порядка, то есть таким решением, в котором при различных значениях C 1 и C 2 можно получить все возможные решения уравнения?
Ответ на этот вопрос следуюший: может, но при некотором условии. Это условие о том, какими свойствами должны обладать частные решения y 1 (x) и y 2 (x) .
И это условие называется условием линейной независимости частных решений.
Теорема. Функция C 1 y 1 (x) + C 2 y 2 (x) является общим решением линейного однородного дифференциального уравнения второго порядка, если функции y 1 (x) и y 2 (x) линейно независимы.
Определение. Функции y 1 (x) и y 2 (x) называются линейно независимыми, если их отношение является константой, отличной от нуля:
Однако установить по определению, являются ли эти функции линейно независимыми, часто очень трудоёмко. Существует способ установления линейной независимости с помощью определителя Вронского W(x) :

Если определитель Вронского не равен нулю, то решения — линейно независимые. Если определитель Вронского равен нулю, то решения — линейно зависимымые.
Пример 1. Найти общее решение линейного однородного дифференциального уравнения 
Решение. Интегрируем дважды и, как легко заметить, чтобы разность второй производной функции и самой функции была равна нулю, решения должны быть связаны с экспонентой, производная которой равна ей самой. То есть частными решениями являются 

Так как определитель Вронского
не равен нулю, то эти решения линейно независимы. Следовательно, общее решение данного уравнения можно записать в виде

Видео:Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентамиСкачать

Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами: теория и практика
Линейным однородным дифференциальным уравнением второго порядка с постоянными коэффициентами называется уравнение вида
где p и q — постоянные величины.
На то, что это уравнение второго порядка, указывает наличие второй производной от искомой функции, а на его однородность — нуль в правой части. Постоянными коэффициентами называются уже упомянутые выше величины.
Чтобы решить линейное однородное дифференциальное уравнение второго порядка с постоянными коэффициентами, нужно сначала решить так называемое характеристическое уравнение вида
которое, как видно, является обычным квадратным уравнением.
В зависимости от решения характеристического уравнения возможны три различных варианта решения линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами, которые сейчас разберём. Для полной определённости будем считать, что все частные решения прошли проверку определителем Вронского и он во всех случаях не равен нулю. Сомневающиеся, впрочем, могут проверить это самостоятельно.
Корни характеристического уравнения — действительные и различные
Иными словами, 

Пример 2. Решить линейное однородное дифференциальное уравнение

Решение. Характеристическое уравнение имеет вид 





Пример 3. Решить линейное однородное дифференциальное уравнение

Решение. Характеристическое уравнение имеет вид 





Корни характеристического уравения — вещественные и равные
То есть, 

Пример 4. Решить линейное однородное дифференциальное уравнение

Решение. Характеристическое уравнение 



Пример 5. Решить линейное однородное дифференциальное уравнение

Решение. Характеристическое уравнение 




Корни характеристического уравнения — комплексные
То есть, 



Пример 6. Решить линейное однородное дифференциальное уравнение

Решение. Характеристическое уравнение 





Пример 7. Решить линейное однородное дифференциальное уравнение

Решение. Характеристическое уравнение 





Решить линейное однородное дифференциальное уравнение с постоянными коэффициентами самостоятельно, а затем посмотреть решение
Пример 8. Решить линейное однородное дифференциальное уравнение

Пример 9. Решить линейное однородное дифференциальное уравнение

Видео:Линейное однородное дифференциальное уравнение 2-го порядка с постоянными коэффициентами.Скачать

Если y1 и y2 два линейно независимых решения дифференциального уравнения
Если же это тождество выполняется лишь при , то указанные функции , , . называются линейно независимыми на отрезке .
Для случая двух функций критерий линейной независимости можно записать в более простом виде: Функции , будут линейно независимыми на отрезке , если их отношение на данном отрезке тождественно не равно постоянной:
В противном случае, при 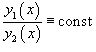
Пусть n функций , , . имеют производные порядка. Определитель
называется определителем Вронского или вронскианом для указанной системы функций.
Теорема . Если система функций , , . линейна зависима на отрезке , то ее определитель Вронского тождественно равен нулю на этом отрезке.
Отсюда следует, что если определитель отличен от нуля хотя бы в одной точке отрезка , то функции , , . будут линейно независимыми. Это свойство определителя Вронского позволяет выяснить, являются ли найденные решения однородного дифференциального уравнения линейно независимыми.
Совокупность двух линейно независимых частных решений линейного однородного дифференциального уравнения второго порядка образует его фундаментальную систему решений .
Если , − фундаментальная система решений, то общее решение уравнения второго порядка представляется в виде
где , − произвольные постоянные.
Заметим, что по заданной фундаментальной системе решений , можно построить соответствующее однородное дифференциальное уравнение. Для случая второго порядка такое уравнение выражается через определитель в виде:
Итак, как указано выше, общее решение однородного дифференциального уравнения второго порядка является линейной комбинацией двух линейно независимых частных решений , этого уравнения.
Очевидно, что частные решения зависят от коэффициентов дифференциального уравнения. Формула Лиувилля-Остроградского устанавливает связь между вронскианом , построенном на базе частных решений , , и коэффициентом в дифференциальном уравнении.
Пусть − определитель Вронского решений , линейного однородного дифференциального уравнения 2-го порядка
К сожалению, общего метода отыскания частного решения не существует. Обычно это можно сделать путем подбора.
Если известно частное решение линейного однородного уравнения второго порядка, то его можно преобразовать к линейному уравнению первого порядка с помощью подстановки и последующей замены .
Другой способ понижения порядка основан на использовании формулы Лиувилля-Остроградского. Здесь также одно частное решение должно быть известно. Соответствующие примеры разобраны ниже.
где , и − непрерывные функции на отрезке .
Соответствующее однородное уравнение записывается в виде
Метод вариации постоянных (или метод Лагранжа) используется для построения общего решения неоднородного уравнения, когда известно общее решение ассоциированного с ним однородного уравнения.
Пусть общее решение однородного уравнения 2-го порядка выражается через фундаментальную систему решений и :
где C1, C2 − произвольные постоянные. Идея данного метода состоит в том, что вместо постоянных C1 и C2рассматриваются функции и , которые подбираются таким образом, чтобы решение удовлетворяло неоднородному уравнению.
Производные неизвестных функций и можно определить из системы уравнений
Применяя метод вариации параметров, важно помнить, что функция должна соответствовать дифференциальному уравнению, приведенному к стандартному виду, т.е. коэффициент перед старшей производной должен быть равен 1.
Далее, зная производные и , можно найти и сами функции и :
Тогда общее решение исходного неоднородного уравнения будет выражаться формулой
Теперь воспользуемся методом вариации постоянных и построим общее решение неоднородного уравнения. Будем рассматривать параметры C1 и C2 как функции от переменной x. Производные этих функций определяются из системы уравнений
В результате получаем общее решение неоднородного уравнения в виде
Видео:Решите уравнение ★ y'-2y=e^(2x) ★ Линейное дифференциальное уравнение 1-го порядкаСкачать
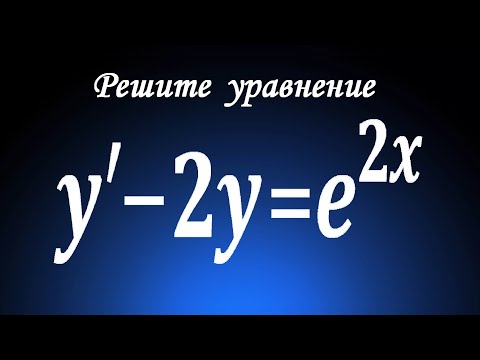
Линейные дифференциальные уравнения второго порядка.
Линейное однородное дифференциальное уравнение (ЛОДУ) второго порядка записывают как:

а линейное неоднородное дифференциальное уравнение (ЛНДУ) второго порядка записывают как:

где функции f(x), p(x) и q(x) являются непрерывными на интервале интегрирования X.
Для понимания того, в каком виде необходимо искать общее решение линейных однородных дифференциальных уравнений и линейных неоднородных дифференциальных уравнений второго порядка необходимо сформулировать 2 теоремы:
Общее решениее y0 ЛОДУ 




Общим решением y ЛНДУ 




- y0=C1⋅y1+C2⋅y2 — является общим решением ЛОДУ
, где y1 и y2 – являются его линейно независимыми частные решения,
- а
— является общим решением ЛНДУ
, где
— является любым из частных решений уравнения, а y0— является общим решением соответствующего линейного однородного дифференциального уравнения.
Теперь рассмотрим методы определения y1, y2 и 
В самых элементарных примерах эти функции вычисляются методом подбора. Линейно независимые функции y1 и y2 чаще всего определяют из наборов:
Проверить линейную независимость функций y1 и y2 можно при помощи определителя Вронского:

Если функции линейно независимы на интервале X, значит, определитель Вронского не равен нулю для всех x из промежутка X.
Например, функции y1 = 1 и y2 = x являются линейно независимыми для всех действительных значений x, потому что

Функции y1 = sinx и y2 = cosx тоже являются линейно независимыми на R, потому что
А функции y1 = — x — 1 и y2 = x + 1 являются линейно зависимыми на интервале (-∞; +∞), потому что
В общем случае определение функций y1, y2 и 
Если удастся подобрать нетривиальное (не равное нулю) частное решение y1 линейного однородного дифференциального уравнения 2-го порядка 

Разберем метод на примере.
Необходимо вычислить общее решение ЛОДУ 2-го порядка 
Хорошо видно, что y1 = x оказывается частным решением исходного уравнения 
откуда 
Вспоминая правило дифференцирования произведения и свойства неопределенного интеграла, получаем

Интегрируем обе части равенства:
произведя потенцирование, записываем общее решение исходного уравнения

где С – является произвольной постоянной.
Т.к. мы принимали 

где F(x) является одной из первообразных функции 
В элементарных функциях первообразная F(x) не выражается.
Решая ЛНДУ второго порядка 

Тогда общее решение линейного однородного дифференциального уравнения будет выглядеть так:
Варьируя произвольные постоянные, общим решением линейного неоднородного дифференциального уравнения принимаем
Производные неизвестных функции C1(x) и C2(x) вычисляются из системы уравнений

а функции C1(x) и C2(x) вычисляются при дальнейшем интегрировании.
💡 Видео
ЛЕКЦИЯ 1.4. Линейно независимые решения и Теорема об общем решенииСкачать

Линейное дифференциальное уравнение первого порядка (1-x^2)*y'-xy=1Скачать

ЛОДУ 2 порядка c постоянными коэффициентамиСкачать

ЛЕКЦИЯ 1.5. Решение однородных линейных дифференциальных уравнений 2-го порядка (с примерами)Скачать

15. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентамиСкачать

Теорема о структуре общего решения линейного однородного дифференциального уравненияСкачать

Однородное линейное дифференциальное уравнение. Алгоритм решенияСкачать

ЛЕКЦИЯ 1.1. Однородные линейные дифференциальные уравнения 2-го порядка: введениеСкачать

Неоднородные линейные дифференциальные уравнения второго порядкаСкачать

Линейные неоднородные дифференциальные уравнения II порядкаСкачать

Линейные однородные дифференциальные уравнения n-го порядка с постоянными коэффициентамСкачать

Лукьяненко Д. В. - Дифференциальные уравнения - Лекция 5Скачать

Линейное неоднородное дифференциальное уравнение - bezbotvyСкачать

Однородные линейные дифференциальные уравнения второго порядкаСкачать



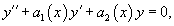
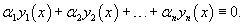
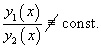
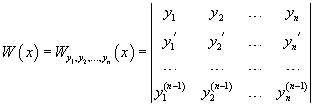
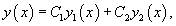
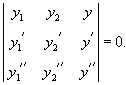
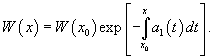
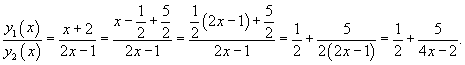
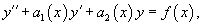
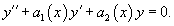

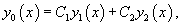
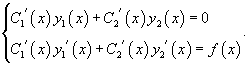
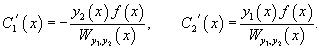
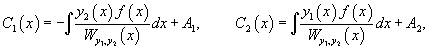
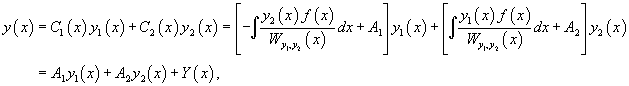
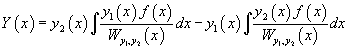
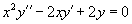
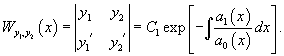
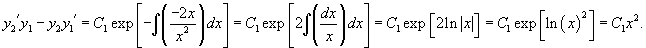
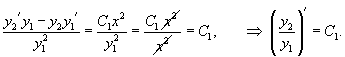
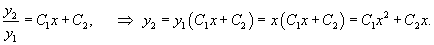
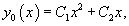
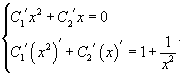
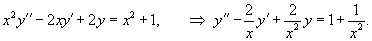
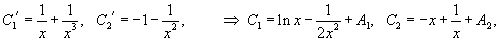
 — является общим решением ЛНДУ
— является общим решением ЛНДУ 




