Если взять в качестве отрезка локализации отрезок 1 2 решение уравнения

Видео:Алгоритмы. Нахождение корней уравнений методом деления отрезка пополам.Скачать

Решение тестов, помощь в закрытии сессии студентам МТИ, Синергии, ГТЕП, Московской Академии Предпринимательства

Видео:Решение тригонометрических уравнений. Подготовка к ЕГЭ | Математика TutorOnlineСкачать

Вычислительная математика тест МОИ и Синергии

Тест Синергии и Московского Открытого Института «Вычислительная математика» Цена 500р.

У числа а*=0,089600 значащие цифры-

Если известно приближенное значение а*=6178 и граница абсолютной погрешности а*=5,6, то можно записать, что а= …

Функция задана своими значениями в узлах х0, х1, …, хn, по этим значениям построены интерполяционные многочлены Ньютона Nn(x) и Лагранжа Ln(x) с оценкой погрешности интерполяции… соответсвенно; тогда…

Округление числа с заданной точностью

Расхождение между точным и приближенным числовым значением+

Результат использования неточных методов вычисления

Сравнивая между собой скорости сходимости метода Якоби (простой итерации) и метода Зейделя, можно утверждать, что…

Метод Зейделя сходится быстрее метода Якоби

Метод Якоби сходится быстрее метода Зейделя

Скорости сходимости этих методов совпадают

Скорости сходимости этих методов сопоставитель нельзя+

Если известны значения фукнции в 7-ми точках, то многочлен Ньютона… степени можно построить, используя все значения функции

Оценка погрешности в методе Рунге- Кутты 4-го порядка точности решения задачи Коги имеет вид

Приближенное значение корня Xn- это такое значение, для которого

Для функции f(x)=e2x верно выражение

Оценка погрешности в методе Эйлера решения задачи Коши имеет вид

Оценка погрешности метода хорд имеет вид

Расчетные формулы метода Якоби (простой итеграции) имеют вид

Верными цифрами числа а*=1,1671, заданного с погрешностью …а*=0,03 являются

Функции f(x)=x5 вычисляется в точке x*=2.02, тогда величина погрешности bf(x*) приближенно равна

Элементарная квадратурная формула трапеции для интеграла… имеет вид

Чтобы число а* содержало ровно 5 верных цифр в узком смысле, нужно найти его с относительной погрешностью

Оценка погрешности в методе Адамса решения задачи Коши имеет вид

Погрешность численного решения задачи определяется

Числом уравнений, составляющих метод решения задачи

Погрешностью представления вещественных числе в ЭВМ

Чувствительностью вычислительного алгоритма к погрешностям округления+

Обусловленностью решаемой задачи

Конечная разность вперед 1-го порядка определяется следующим образом

Отрезок локализации корня уравнения f(x)=0 это отрезок

Содержащий только один корень уравнения+

Границы которого- корни уравнения

Содержащий по крайней мере один корень уравнения

Содержащий все корни уравнения

Если взять в качестве отрезка локализации отрезок [1; 2] решение уравнения x4-6x+9=0

Можно найти методом половинного деления, так как функция непрерывна+

Нельзя найти методом половинного деления, так как уравнение решается только прямым методом

Нельзя найти методом половинного деления, так как условия применимости метода не выполняются

Можно найти методом половинного деления, так как отрезок локализации указан правильно

Функция f(x,y)=3*y-5*x3 вычисляется в точке (x*,y*)= (0.23; 0.31), тогда величина погрешности f(x*, y*) приближенно равна

Нормой матрицы А, согласованной с нормой вектора х, называется величина

Расчетная формула метода Ньютона имеет вид

Достаточное условие сходимости метода Якоби (простой итерации) можно выразить как

Результат округления числа а*=0,026974 до трех значащих цифр равен

Пусть уравнение f(x)=0 преобразованно к виду, удобному для итерации x=f(x)- тогда для сходимости метода простой итерации в некоторой окрестности корня должно выполняться условие

Интерполирование многочленом Лагранжа 2-ой степени обеспечивает порядок… точности по h

Погрешность численного решения задачи определяется

• 33.333%обусловленностью решаемой задачи
• 33.333%чувствительностью вычислительного алгоритма к погрешностям округления
• 33.333%погрешностью представления вещественных чисел в ЭВМ

Сигналы, зарегистрированные на материальном носителе называются…

Функция задана своими значениями в узлах . По этим значениям строят интерполяционные многочлены Ньютона и Лагранжа . Какое утверждение верно:

Функция задана своими значениями в узлах . По этим значениям строят интерполяционные многочлены Ньютона и Лагранжа с погрешностями интерполяции и соответственно. Какое утверждение верно:

Построение интерполирующей функции, в общем случае, подчиняется условию:

Равенства интерполирующей и интерполируемой функций в конечном множестве точек из интервала приближения

Построение полинома наилучшего равномерного приближения (n-го порядка) непрерывной функции на конечном интервале [a,b] предполагает достижение:

Минимума максимального (по модулю) уклонения полинома от приближаемой функции на конечном множестве точек из интервала приближения

Единственность решения задачи полиномиального интерполирования обеспечивается:

выполнением условий интерполирования в n+1 (n-порядок полинома) точке из интервала приближения

Качество построения интерполяционного полинома оценивается:

Максимумом модуля уклонения полинома от приближаемой функции в узлах сетки

Процесс полиномиального интерполирования сходится равномерно, если

Стремится к нулю величина максимума модуля разности полинома и приближаемой функции на интервале приближения при неограниченном росте порядка полинома

На каком из рисунков представлена функция уклонения , соответствующая полиному наилучшего равномерного приближения пятого порядка?

Отрезок ряда Тейлора для функции f(x), содержащий n+1 слагаемое, является

Интерполяционным полиномом n-го порядка, построенным на сетке, содержащей один узел кратности n+1

Максимум модуля уклонения интерполяционного полинома от приближаемой функции в сравнении с максимумом модуля уклонения полинома наилучшего равномерного приближения может быть:

Только не меньше

Сплайн является «естественным» если:

Оценка погрешности сплайн-интерполирования вида : , где и справедлива для:

Для фундаментального кубического сплайна

На каком из рисунков представлена функция уклонения, соответствующая интерполяционному полиному 6-го порядка, построенному на чебышевской сетке:

Нормальная система метода наименьших квадратов это:

Система линейных алгебраических уравнений для нахождения коэффициентов приближающего многочлена

Функция интерполируется по точкам . Оценить теоретическую погрешность интерполяции на отрезке

Для погрешности интерполяции многочленом Лагранжа первой степени справедлива оценка:

Известны значения функции в 7-ми точках. Многочлен Ньютона какой степени можно построить по этой таблице, используя все значения функции?

Интерполирование многочленом Ньютона 5-ой степени обеспечивает порядок точности по :

Функция задана таблицей . Cреднеквадратичное уклонение многочлена :

Является ли интерполяционным сплайном многочлен степени N, построенный по заданным значениям функции в узлах

Да, это сплайн степени n дефекта 0

Конечная разность вперед порядка определяется следующим образом:

Интерполирование многочленом Лагранжа 2-ой степени обеспечивает порядок точности по :

Среднеквадратичное уклонение многочлена от функции, заданной в точках – это:

Величина погрешности интерполяции функции в точке при интерполировании по узлам приближенно равна:

Граничные условия естественного кубического сплайна S(x) имеют вид:

Функция задана своими значениями в узлах . По этим значениям строят интерполяционные многочлены Ньютона и Лагранжа . Какое утверждение верно:

Функция интерполируется по точкам . Оценить теоретическую погрешность интерполяции на отрезке [0, 1]

Какой из приведенных ниже многочленов является интерполяционным для функции, заданной таблицей :

Функция задана таблицей своих значений в точках . Многочлен Лагранжа какой степени можно построить по этой таблице, используя все значения функции?

Величина погрешности интерполяции функции в точке при интерполировании по узлам приближенно равна:

Качество приближения функции интерполяционным полиномом может оцениваться:

• величиной среднеквадратичного уклонения полинома от приближаемой функции на интервале приближения
• максимумом уклонения полинома от приближаемой функции на интервале приближения

Процесс полиномиального интерполирования непрерывной функции:

• всегда сходится на какой-либо системе сеток
• может расходиться на любой из сеток (в зависимости от свойств функции)

Полиномиальное интерполирование на чебышевской сетке:

• всегда сходится на какой-либо системе сеток
• может расходиться на любой из сеток (в зависимости от свойств функции)

Чебышевское интерполирование это:

• это интерполирование на сетке из (n+2) узлов
• построение полинома n-го порядка, имеющего равные по модулю и последовательно изменяющие знак уклонения в заранее заданных n+2 точка if из интервала приближения

Полином является полиномом наилучшего равномерного приближения на [a,b] непрерывной функции если:

• существует такая последовательность из (n+2) точек , в которых справедливы следующие соотношения и if
• он осуществляет чебышевскую интерполяцию на экстремальном базисе

• реализовать сходящийся процесс интерполирования
• использовать интерполяционную функцию для вычисления производных приближаемой функции
• решить задачу интерполирования полиномами невысоких степеней

Полином наилучшего среднеквадратичного приближения функции f(x), заданной на множестве точек : i=0,1,2, …, N, можно получить:

• посредством поиска экстремума (минимума) функци
• посредством нахождения нормального псевдорешения системы линейных уравнений

Полином Лагранжа и полином Ньютона, построенные на одних и тех же узловых точках

Кубический сплайн и функция Лагранжа, построенные на одних и тех же узловых точках

могут отличаться при других значений аргумента

Полином Ньютона и кубический сплайн, построенные на одних и тех же узловых точках

Задача отыскания приближения к корню уравнения с заданной точностью состоит в поиске числа , удовлетворяющего условию:

Метод бисекции является:

Итерационным методом решения уравнения

Апостериорная оценка погрешности для метода простой итерации имеет вид:

Методом Ньютона решается уравнение:

Расчетная формула имеет вид:

Радиус интервала неопределенности простого корня уравнения можно вычислить по формуле:

Уравнение имеет вид: Что можно сказать о корнях функции:

Первый корень – кратный, второй – простой

Оценка погрешности в методе бисекции имеет вид:

Критерий окончания для метода простой итерации имеет вид:

Расчетная формула метода Ньютона имеет вид:

Число обусловленности задачи нахождения простого корня имеет вид:

Приближенное значение корня — это такое значение, для которого выполняется условие:

Абсолютная погрешность не превышает

Дано уравнение: . Применяется метод Ньютона с начальным приближением . С какой точностью будет получен корень уравнения после 2-х шагов по методу Ньютона :

Для достижения точности применяют следующий критерий окончания метода бисекций :

Пусть уравнение преобразовано к виду удобному для итерации . Условие сходимости метода простой итерации: в некоторой — окрестности корня должно выполняться условие:

Известен радиус неопределенности простого корня уравнения. С какой точностью можно вычислить корень :

Сколько вещественных корней имеет уравнение :

Первая и вторая производная функции f(x) должны сохранять свой знак для уточнения корня методами:

1. Какие из приведенных методов относятся к методам решения нелинейного уравнения:

• 33.333% Метод Ньютона
• 33.333% Метод деления пополам
• 33.333% Метод хорд

1. Что из перечисленного НЕ относится к методу простой итерации

• 50% метод хорд
• 50% метод половинного деления

является методом расчета определенного интеграла

Метод Ньютона — это метод уточнения корня.

Метод постой итерации, в котором устанавливается требование равенства нулю для первой производной от величины (f(x)-x), называется методом Ньютона

Правило рунге оценки погрешности для формул прямоугольников и трапеций имеет вид

Обратная задача теории погрешностей-это Округление числа с заданной точностью и вычисление общей погрешности Определение погрешности, с которой допустимо использовать аргументы, так чтобы погрешность функции не превосходит заданной величины Получение точного значения числа, зная его приближенное значение и величину погрешности

результат округления числа 0.026974 до трех значащих цифр равен

Погрешность-это… Округление числа с заданной точностью Расхождение между точным и приближенным числовым значением Результат использования неточных методов вычисления

результат округления числа 0.05695 до трех значащих цифр равен

Подинтегральная функция интерполируется многочленом 1-й степени, построенным по значениям функции в концах отрезка интегрирования- при интегрировании этого многочлена получается элементарная формула Симпсона Трапеций Левых прямоугольников Центральных прямоугольников

Сравнивая между собой скорости сходимости метода Якоби (простой итерации) и метода Зейделя, можно утверждать, что Метод Зейделя сходится быстрее метода Якоби Метод Якоби сходится быстрее метода Зейделя Скорости сходимости с этих методов совпадают Скорости сходимости этих методов сопоставить нельзя

Расчетные формулы метода Якоби (простой интеграции) имеют вид

Достаточное условие сходимости метода Якоби (простой итерации) можно выразить как

Правило четной цифры при округлении означает, что если при округлении Отбрасываемые цифры составляют четное число, то последняя оставляемая цифра остается без изменения Цифра старшего отбрасываемого разряда четная, то предыдущая цифра остается без изменения, иначе увеличивается на единицу Отбрасываемые цифры составляют ровно половину единицы последнего оставляемого разряда, то последняя оставляемая цифра остается без изменения, если она четная, и увеличивается на единицу, если не четная

Норма вектора x = (10, -10, 0, -1) равна … Тип ответа: Одиночный выбор 21 10 1

Значащая цифра называется верной если … Тип ответа: Одиночный выбор относительная погрешность числа не превосходит 50% абсолютная погрешность числа не превосходит половины единицы разряда, в котором стоит значащая цифра она отлична от нуля

Приближенное число = 0,0410 задано со всеми верными цифрами в широком смысле — тогда относительная погрешность числа равна … Тип ответа: Одиночный выбор 0.00001% 2.5% 0.25% 0.03%

Задача отыскания приближения к корню уравнения с заданной точностью состоит в поиске числа , удовлетворяющего условию:

Машинный эпсилон — это:

Относительная погрешность представления вещественных чисел в ЭВМ

Как соотносятся машинный нуль и машинный эпсилон ?

Машинный эпсилон больше машинного нуля

Какой из приведенных ниже алгоритмов даст верный результат вычисления выражения (1.0е-3 +1 — 1) в машинной системе с основанием 10, числом разрядов в мантиссе равном 3 и округлением посредством отбрасывания разрядов.

АЛГОРИТМ 1. fl[fl(1.0e-3 +1) — 1]

АЛГОРИТМ 2. fl[fl(1.0e-3) — fl(1-1)]

Обратный анализ ошибок позволяет

Получить оценку близости решенной задачи к исходной (той, которую хотели решить)

Результат округления до трех значащих цифр числа усечением:

Приближенное число задано со всеми верными цифрами. Относительная погрешность числа равна:

Функция вычисляется в точке (округление произведено по дополнению). Величина погрешности приближенно равна:

Для числа известно приближенное значение и граница абсолютной погрешности . Правильная запись:

Дана функция . Какое неравенство неверное:

Значащие цифры числа :

Функция вычисляется в точке , причем погрешность каждого аргумента составляет 2%. Величина погрешности приближенно равна:

Какое неравенство верное:

Верными цифрами числа , заданного с погрешностью , являются:

Два приближенных числа и заданы со всеми верными цифрами. Выберите неверное утверждение:

Числа и заданы с одинаковой точностью

Чему равно относительное число обусловленности задачи вычисления функции , если аргумент :

С какой относительной погрешностью нужно найти число , чтобы оно содержало ровно 5 верных цифр:

Два приближенных числа и заданы со всеми верными цифрами. Выберите верное утверждение:

Числа заданы с одинаковой относительной погрешностью

Функция вычисляется в точке (округление произведено по дополнению). Величина погрешности приближенно равна:

Чему равно абсолютное число обусловленности задачи вычисления функции , если аргумент :

Машинный нуль –это:

Минимальное представимое в ЭВМ положительное число

Функция вычисляется в точке (округление произведено по дополнению). Величина погрешности приближенно равна:

Метод бисекции является:

Итерационным методом решения уравнения

Множество машинных чисел

• 50%дискретно
• 50%ограничено и сверху и снизу

В вычислительных алгоритмах для формирования критериев останова итерационных процессов, оценки обусловленности задачи следует использовать

• 50%машинный эпсилон
• 50%константы, задаваемые пользователем

Ошибка дискретизации это:

• 33.333%ошибка, связанная с переходом к дискретным независимым переменным в мат. Модели
• 33.333%ошибка, порождаемая при переходе от непрерывной мат. модели к дискретной
• 33.333%разность значений точного решения системы уравнений непрерывной мат.модели и значения точного решения системы уравнений дискретной мат.модели

Численный метод корректен, если он

• 50%ее решение непрерывно по исходным данным
• 50%ее решение существует и единственно

Функция приближается интерполяционным многочленом Ньютона 1-й степени по узлам xi, xi+1 , тогда коэффициент при старшей степени x: … Тип ответа: Одиночный выбор

Оценка погрешности в методе половинного деления имеет вид: … Тип ответа: Одиночный выбор

Видео:1,2 Решение нелинейных уравнений методом хордСкачать

Фрагмент решения задачи 2.1

ЛАБОРАТОРНАЯ РАБОТА № 2.

РЕШЕНИЕ НЕЛИНЕЙНЫХ УРАВНЕНИЙ

Цель: сформировать навыки решения нелинейных уравнений численными методами.

Отчетпо лабораторной работе должен содержать следующие материалы по каждой задаче:

1) постановка задачи;

2) необходимый теоретический материал;

3) результаты вычислительного эксперимента;

4) анализ полученных результатов;

5) графический материал (если необходимо);

6) тексты программ.

Варианты заданий к задачам 2.1-2.10 даны в ПРИЛОЖЕНИИ 2.A.

Основные теоретические сведения

1.1.Пусть задана непрерывная функция f(x) и требуется найти корни уравнения

на всей числовой оси или на некотором интервале .

Всякое значение , удовлетворяющее условию , называется корнем уравнения (1), а способ нахождения этого значения — решением уравнения (1).

Численное решение уравнения проводится в два этапа:

1 этап. Отделение корней уравнения.

2 этап. Уточнение интересующих корней с заданной точностью ε.

Отделение корней – это определение их наличия, количества и нахождение для каждого их них достаточно малого отрезка [a,b], которому он принадлежит.

Уточнение корня – это вычисление интересующего корня с заданной точностью e.

Расчетные формулы методов решения нелинейного уравнения .

Метод дихотомии (половинного деления, бисекций):

x = (a+b)/2 , если ¦(a) ·¦(x)>0 => x * Î [x,b] => a=x, иначе x * Î [a, x] => b=x

Оценка количества итераций n, требуемых для достижения требуемой точности ε (на заданном отрезке [a,b]):

Условие завершения вычислений : длина отрезка не превышает заданную точность и значение функции близко к 0 с заданной точностью:

Метод простых итераций (метод последовательных приближений).

Условие сходимости

Условие завершения итерационного процесса:

Упрощенный метод Ньютона: , n=0,1,…

Условие окончания расчета:

,

где −корректирующее приращение или поправка.

Условие сходимости итерационного процесса:

Метод ложного положения: , n=0,1,…;

c-фиксированная точка из окрестности корня

Метод секущих: , n=0,1,…

Метод Стеффенсена: , n=0,1,…

Модифицированный метод Ньютона для поиска кратных корней:

, n=0,1,…, m=1,2,…

Индивидуальные задания

Задача 2.1. Даны два уравнения f(x)=0 и g(x)=0. Найти с точностью все корни уравнений, содержащиеся на отрезке [a, b]. Для решения задачи использовать метод бисекции.

ПОРЯДОК РЕШЕНИЯ ЗАДАЧИ:

1. Найти аналитическое решение уравнения f(x)=0.

2. Локализовать корни f(x)=0 графически.

3. Найти корни уравнения f(x)=0 с точностью с помощью метода бисекции.

4. Найти корни уравнения f(x)=0 с точностью .

5. Аналогично п. 1-4 попытаться найти корни уравнения g(x)=0. Объяснить полученные результаты.

Фрагмент решения задачи 2.1.

=0, [a,b]=[0,]

Аналитическое решение задачи:

, =1.31811607652818, =1.738244406014586

Численное решение задачи: Локализация корней для численного решения задачи:

(на примере работы пакета MATHCAD)

bisec

Встроенная функция пакета MATHCAD

— задание начального приближения

Значение корня отличается от найденного с помощью функции bisec , так как по умолчанию величина погрешности при работе встроенных функций равна 0.001.

Переопределим параметр для задания погрешности

Значение корня с заданной точностью 1.3181160717.

bisec

Значение корня с заданной точностью 1.7382444060, число итераций 32.

— задание начального приближения

.

Значения корней в пределах заданной точности совпадают.

Задача 2.2.Найти указанный в варианте корень уравнения f(x)=0 с точностью , двумя способами.

а) Использовать метод бисекции. Предварительно определить отрезок локализации [a, b].

b) Использовать метод Ньютона. В качестве начального приближения для метода Ньютона взять середину отрезка локализации из п. а).

Сравнить число итераций в п. a), b).

Задача 2.3.Локализовать корни уравнения f(x)=0 и найти их с точностью , используя метод простой итерации. К виду x=j(x), удобному для итераций, уравнение f(x)=0 привести двумя способами.

a) Преобразовать уравнение к виду x=x-af(x), где a=2/(M+m), , а x принадлежит отрезку локализации [a, b].

b) Любым другим преобразованием уравнения. Проверить достаточное условие сходимости метода.

Использовать критерий окончания итерационного процесса вида , где в п. a) q=(M-m)/(M+m), в п. b) .

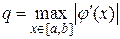
Сравнить число итераций и значения величины q в п. a), b).

Задача 2.4.Локализовать корни уравнения f(x)=0. Найти их с точностью , используя методы простой итерации и Ньютона. Сравнить скорость сходимости методов (по числу итераций).

Задача 2.5.Найти приближенно корень уравнения f(x)=0, принадлежащий отрезку [a,b], с точностью , используя модификацию метода Ньютона для случая кратного корня при значениях m=1,2,3,4,5. По числу итераций определить кратность корня.

Задача 2.6.(ИНДИВИДУАЛЬНОЕ ДОМАШНЕЕ ЗАДАНИЕ)

Локализовать корни уравнения f(x)=0. Найти их с точностью и , используя метод Ньютона и метод, указанный в индивидуальном варианте. Сравнить скорость сходимости методов (по числу итераций) для каждого значения .

Задача 2.7.Локализовать корни уравнения f(x)=0. Найти их с точностью и , используя метод Ньютона, упрощенный метод Ньютона и метод секущих. Сравнить скорость сходимости методов (по числу итераций) для каждого значения .

Задача 2.8.(ИНДИВИДУАЛЬНОЕ ДОМАШНЕЕ ЗАДАНИЕ)

Найти приближенно все (в том числе комплексные) корни уравнения f(x)=0 с точностью , используя метод Ньютона.

УКАЗАНИЕ. Для поиска комплексных корней следует использовать комплексные начальные приближения.

Задача 2.9.(ИНДИВИДУАЛЬНОЕ ДОМАШНЕЕ ЗАДАНИЕ)

a)Локализовать корни уравнения f(x)=0. Уточнить их с точностью , используя метод Ньютона. Для поиска кратного корня и определения его кратности следует использовать модификацию метода Ньютона для случая кратного корня с m=1,2,3. При любых ли начальных приближениях такой метод сходится?

b) Рассмотреть уравнение f(x)+d=0, где 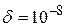. Найти корень кратности 1, используя метод Ньютона. Применить для нахождения кратного корня соответствующую модификацию* метода Ньютона. Удается ли найти кратный корень? Если нет, то использовать метод Ньютона с комплексными начальными приближениями. Сохранился ли кратный корень? Объяснить результаты.

Задача 2.10.(ИНДИВИДУАЛЬНОЕ ДОМАШНЕЕ ЗАДАНИЕ)

Функция y=f(x) задана неявно уравнением F(x,y)=0. На отрезке [1, 5] построить таблицу значений функции y=f(x) с шагом h=0.5, применяя один из методов численного решения нелинейного уравнения (с точностью ). Построить график функции y=f(x) на заданном отрезке.

ПРИЛОЖЕНИЕ 2.A.

ВАРИАНТЫ ЗАДАНИЙ К ЛАБОРАТОРНОЙ РАБОТЕ 2

Таблица к задаче 2.1

N	f(x)	g(x)	[a, b]
2.1.1
2.1.2
2.1.3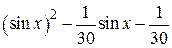
2.1.4
2.1.5
2.1.6
2.1.7.			[5,25]
2.1.8			[0.1,10]
2.1.9			[0.1,2]
2.1.10
2.1.11
2.1.12
2.1.13			[0,3]
2.1.14			[0,2]
2.1.15			[0,3]
2.1.16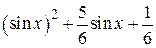
2.1.17
2.1.18
2.1.19
2.1.20
2.1.21
2.1.22			[0.001,3]
2.1.23			[0.1,35]
2.1.24			[0.01,3]
2.1.25
2.1.26			[-0.5,1.5]
2.1.27			[-1.5,0]
2.1.28			[1,3]
2.1.29			[0,3]
2.1.30			[0,5]

Таблица к задаче 2.2 Таблица к задаче 2.3

N	f(x)	Найти корень	N	f(x)
2.2.1		отрицательный	2.3.1
2.2.2		положительный	2.3.2
2.2.3		положительный	2.3.3
2.2.4		наибольший по модулю	2.3.4
2.2.5		все корни	2.3.5

Таблица к задаче 2.4

f(x)
N
2.4.1	4.545004	-3.055105	-18.06895	4.002429	4.722482
2.4.2	-2.656764	-3.406111	10.89372	-1.752935	-3.423612
2.4.3	-4.556062	2.93309	9.274868	-10.32081	0.422098
2.4.4	7.809249	16.28542	-2.771356	-27.95304	-11.33921
2.4.5	-13.0072	60.24546	-122.0716	105.6798	-30.19201

Таблица к задаче 2.5

N	f(x)	[a, b]
2.5.1		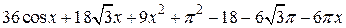[0.8,1.2]
2.5.2		[0.3,0.7]
2.5.3		[0.5,1]
2.5.4		[0,1]
2.5.5		[0,0.7]

Таблица к задаче 2.6 Таблица к задаче 2.7

N	f(x)	Метод*	N	f(x)
2.6.1		упрощенный метод Ньютона	2.7.1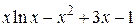
2.6.2		метод ложного положения	2.7.2
2.6.3		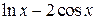метод простой итерации	2.7.3
2.6.4		метод секущих	2.7.4
2.6.5		метод Стеффенсена	2.7.5

Таблица к задаче 2.8 Таблица к задаче 2.9

N	f(x)	N	f(x)
2.8.1		2.9.1
2.8.2		2.9.2
2.8.3		2.9.3
2.8.4		2.9.4
2.8.5		2.9.5

Таблица к задаче 2.10

N	F(x,y)
2.10.1	, ,
2.10.2	, ,
2.10.3	, ,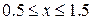
2.10.4	, ,
2.10.5	, ,

Контрольные вопросы

1. Опишите этапы численного решения уравнений

2. Опишите схему алгоритма отделения корней

3. Перечислите алгоритмы уточнения корней уравнения

4. Опишите методы уточнения корней уравнения

5. Опишите схему алгоритма метода бисекций (дихотомии)

6. Как рассчитать количество итераций n, требуемых для достижения требуемой точности ε

7. Объясните алгоритм решения нелинейного уравнения методом
простых итераций

8. Объясните схему алгоритма метода Ньютона

9. Объясните формулы итерационных процессов численного решения уравнений

1. Амосов А.А., Дубинский Ю.А., Копченова Н.В. Вычислительные методы для инженеров. М.: Высшая школа, 1994.

Видео:Три способа отбора корней в задании 13 ЕГЭ профильСкачать

Сходимость метода Ньютона

Выясним основные условия сходимости последовательности значений , вычисляемых по формуле (2.15), к корню уравнения (2.1). Предполагая, что дважды непрерывно дифференцируема, разложим в ряд Тейлора в окрестности k-го приближения

Разделив последнее соотношение на и перенеся часть слагаемых из левой части в правую, получим:

Учитывая, что выражение в квадратных скобках согласно (2.15) равно , переписываем это соотношение в виде

Из (2.16) следует оценка

Очевидно, что ошибка убывает, если

Полученное условие означает, что сходимость зависит от выбора начального приближения.

Оценка (2.17) характеризует скорость убывания погрешности для метода Ньютона: на каждом шаге погрешность пропорциональна квадрату погрешности на предыдущем шаге. Следовательно, метод Ньютона обладает квадратичной сходимостью.

Видео:5. Решение волнового уравнения на отрезке методом ФурьеСкачать

Выбор начального приближения в методе Ньютона

Как следует из условия (2.18) сходимость итерационной последовательности, получаемой в методе Ньютона, зависит от выбора начального приближения . Это можно заметить и из геометрической интерпретации метода. Так, если в качестве начального приближения взять точку (рис. 2.9), то на сходимость итерационного процесса рассчитывать не приходится.

Если же в качестве начального приближения выбрать точку , то получим сходящуюся последовательность.

В общем случае, если задан отрезок , содержащий корень, и известно, что функция монотонна на этом отрезке, то в качестве начального приближения можно выбрать ту границу отрезка , где совпадают знаки функции и второй производной . Такой выбор начального приближения гарантирует сходимость метода Ньютона при условии монотонности функции на отрезке локализации корня.

Видео:Тригонометрические уравнения. ЕГЭ № 12 | Математика | TutorOnline tutor onlineСкачать

1 Численный метод решения нелинейных уравнений

Видео:Я теряю корни ★ 99 ошиблись ★ Решите уравнение ★ x^x=(1/2)^(1/2)Скачать

1.1 Область локализации корней

В общем виде любое уравнение одной переменной принято записывать так , при этом корнем (решением) называется такое значение x*, что оказывается верным тождеством. Уравнение может иметь один, несколько (включая бесконечное число) или ни одного корня. Как легко видеть, для действительных корней задача отыскания решения уравнения легко интерпретируется графически: корень есть такое значение независимой переменной, при котором происходит пересечение графика функции, стоящей в левой части уравнения f ( x ), с осью абсцисс.

Например , для уравнения выполним преобразование и приведем его к виду f(x)= 0 т.е. . График этой функции представлен на рисунке 1. Очевидно, что данное уравнение имеет два действительных корня – один на отрезке [-1, 0] , а второй – [1, 2].

Рисунок 1. График функции

Таким образом, можно приблизительно определять область локализации корней уравнения. Заметим, что отделить корень можно не единственным образом: если корень отделён на каком-либо отрезке, то годится и любой меньший отрезок, содержащий этот корень. Вообще говоря, чем меньше отрезок, тем лучше, но при этом не следует забывать о том, что на отделение корня на меньших отрезках также тратятся вычислительные усилия, и, быть может, весьма значительные. Таким образом, часто для начала довольствуются весьма широким отрезком, на котором корень отделён.

Некоторые виды уравнений допускают аналитическое решение. Например, степенные алгебраические уравнения степени n при n ≤ 4. Однако, в общем виде, аналитическое решение, как правило, отсутствует. В этом случае, применяются численные методы. Все численные методы решения уравнений представляют собой итерационные алгоритмы последовательного приближения к корню уравнения. То есть, выбирается начальное приближение к корню x ₀ и затем с помощью итерационной формулы генерируется последовательность x ₁, x ₂, …, x_k сходящаяся к корню уравнения .

Видео:Как решать Диофантовы уравнения ★ 9x+13y=-1 ★ Решите уравнение в целых числахСкачать

1.2 Критерии сходимости при решении уравнений

Ø Абсолютная погрешность — абсолютное изменение приближения на соседних шагах итерации

Ø Относительная погрешность — относительное изменение приближения на соседних шагах итерации

Ø Близость к нулю вычисленного значения левой части уравнения (иногда это значение называют невязкой уравнения, так как для корня невязка равна нулю)

Видео:Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

1.3 Метод половинного деления (метод дихотомии)

Метод половинного деления основан на последовательном делении отрезка локализации корня пополам.

Для этого выбирается начальное приближение к отрезку [ a , b ], такое, что f ( a ) × f ( b ) — середине отрезка [ a , b ]. Если он противоположен знаку функции в точке a, то корень локализован на отрезке [ a , c ], если же нет – то на отрезке [ c , b ]. Схема метода дихотомии приведен на рис у нке 2.

Рисунок 2. Последовательное деление отрезка пополам и приближение к корню

Алгоритм метода дихотомии можно записать так:

1. представить решаемое уравнение в виде

2. выбрать a, b и вычислить

3. если f(a) × f( с ) то a=a; b = c иначе a = c; b=b

4. если критерий сходимости не выполнен, то перейти к п. 2

Видео:Метод Ньютона (метод касательных) Пример РешенияСкачать

Пример решения уравнения методом дихотомии

Найти решение заданного уравнения методом дихотомии с точностью до 10 -5 .

Пример создания расчетной схемы на основе метода дихотомии на примере уравнения: на отрезке [1, 2]

Данный метод заключается в проверке на каждой итерации условия:

если f ( a ) × f (с) и выбор соответствующего отрезка для следующей итерации.

Рисунок 3. Последовательность итераций метода дихотомии при поиске корня уравнения на отрезке [1, 2]

a ) схема расчета (зависимые ячейки); b) режим отображения формул;

Для нашего примера итерационная последовательность для нахождения решения принимает вид:

Точность до пятой значащей цифры достигается за 20 итераций.

Скорость сходимости этого метода является линейной.

При выполнении начального условия он сходится к решению всегда.

Метод половинного деления удобен при решении физически реальных уравнений, когда заранее известен отрезок локализации решения уравнения.

Видео:Метод Фурье для неоднородного уравнения теплопроводностиСкачать

2 Решение уравнений , используя “Подбор параметра ”

Используя возможности Excel можно находить корни нелинейного уравнения вида f(x)=0 в допустимой области определения переменной. Последовательность операций нахождения корней следующая:

1. Производится табулирование функции в диапазоне вероятного существования корней;

2. По таблице фиксируются ближайшие приближения к значениям корней;

3. Используя средство Excel Подбор параметра, вычисляются корни уравнения с заданной точностью.

При подборе параметра Excel использует итерационный (циклический) процесс. Количество итераций и точность устанавливаются в меню Сервис/Параметры/вкладка Вычисления. Если Excel выполняет сложную задачу подбора параметра, можно нажать кнопку Пауза в окне диалога Результат подбора параметра и прервать вычисление, а затем нажать кнопку Шаг, чтобы выполнить очередную итерацию и просмотреть результат. При решении задачи в пошаговом режиме появляется кнопка П родолжить — для возврата в обычный режим подбора параметра.

Видео:Как составить уравнение прямой, проходящей через две точки на плоскости | МатематикаСкачать

2.1 Пример решения уравнения, используя “Подбор параметра”

Например , найдем все корни уравнения 2x 3 -15sin(x)+0,5x-5=0 на отрезке [-3 ; 3].

Для локализации начальных приближений необходимо определить интервалы значений Х, внутри которых значение функции пересекает ось абсцисс, т.е. функция меняет знак. С этой целью табулируем функцию на отрезке [–3; 3] с шагом 0,2, получим табличные значения функции. Из полученной таблицы находим, что значение функции трижды пересекает ось Х, следовательно, исходное уравнение имеет на заданном отрезке все три корня.

Рисунок 4. Поиск приближенных значений корней уравнения

Выполните команду меню Сервис/Параметры, во вкладке Вычисления установите относительную погрешность вычислений E=0,00001, а число итераций N=1000, установите флажок Итерации.

Выполните команду меню Сервис/Подбор параметра. В диалоговом окне (рисунок 9) заполните следующие поля:

þ Установить в ячейке : в поле указывается адрес ячейки, в которой записана формула правой части функции;

þ Значение : в поле указывается значение, которое должен получить полином в результате вычислений, т.е. правая часть уравнения (в нашем случае 0);

þ Изменяя значение : в поле указывается адрес ячейки (где записано начальное приближение), в которой будет вычисляться корень уравнения и на которую ссылается формула.

Рисунок 5. Диалоговое окно Подбор параметра для поиска первого корня

После щелчка на ОК получим значение первого корня -1,65793685 .

Выполняя последовательно операции аналогичные предыдущим, вычислим значения остальных корней: -0,35913476 и 2,05170101 .

Видео:1.1 Решение нелинейных уравнений метод деления отрезка пополам (бисекций) Мathcad15Скачать

3 Решение уравнений и систем уравнений, используя надстройку “Поиск решения”

Для решения уравнений можно также использовать команду Поиск решения, доступ к которой реализуется через пункт меню Сервис/Поиск решения.

Последовательность операций нахождения корней следующая:

1. Найти приближенное значение корня уравнения

2. Открыть диалог Поиск решения и установить следующие параметры (рисунок 10):

þ в поле У становить целевую ячейку ввести адрес ячейки, содержащей формулу (левую часть уравнения);

þ установить переключатель в положение ‘ значению’ и ввести значение 0 (правая часть уравнения);

þ в поле Изменяя ячейки ввести адреса изменяемых ячеек, т.е. аргумента x целевой функции,;

þ в поле Ограничения с помощью кнопки Д обавить ввести все ограничения, которым должен отвечать результат поиска (область поиска корня уравнения);

þ для запуска процесса поиска решения нажать кнопку В ыполнить.

þ Для сохранения полученного решения необходимо использовать переключатель С охранить найденное решение в открывшемся окне диалога Результаты поиска решения.

Рисунок 6. Диалоговое окно Поиск решения

Полученное решение зависит от выбора начального приближения. Поиск начальных приближений рассмотрен выше.

Рассмотрим некоторые Опции, управляющие работой Поиска решения, задаваемые в окне Параметры (окно появляется, если нажать на кнопку Параметры окна Поиск решения):

þ Максимальное время — ограничивает время, отведенное на процесс поиска решения (по умолчанию задано 100 секунд, что достаточно для задач, имеющих около 10 ограничений, если задача большой размерности, то время необходимо увеличить).

þ Относительная погрешность — задает точность, с которой определяется соответствие ячейки целевому значению или приближение к указанным ограничениям (десятичная дробь от 0 до 1).

þ Неотрицательные значения — этим флажком можно задать ограничения на переменные, что позволит искать решения в положительной области значений, не задавая специальных ограничений на их нижнюю границу.

þ Показывать результаты итераций — этот флажок позволяет включить пошаговый процесс поиска, показывая на экране результаты каждой итерации.

þ Метод поиска — служит для выбора алгоритма оптимизации. Метод Ньютона был рассмотрен ранее. В Методе сопряженных градиентов запрашивается меньше памяти, но выполняется больше итераций, чем в методе Ньютона. Данный метод следует использовать, если задача достаточно велика и если итерации дают слишком малое отличие в последовательных приближениях.

Рисунок 7. Вкладка Параметры окна Поиск решения

Видео:СЛОЖИТЕ ДВА КОРНЯСкачать

3.1 Пример решения уравнения, используя надстройку “Поиск решения”

Например , найдем все корни уравнения 2x 3 -15sin(x)+0,5x-5=0 на отрезке [-3 ; 3]. Для локализации начальных приближений необходимо определить интервалы значений Х, внутри которых значение функции пересекает ось абсцисс, т.е. функция меняет знак. С этой целью табулируем функцию на отрезке [–3;3] с шагом 0,2, получим табличные значения функции. Из полученной таблицы находим, что значение функции трижды пересекает ось Х, следовательно, исходное уравнение имеет на заданном отрезке все три корня. На рисунке 12 представлен пример заполнения окна Поиск решения для нахождения первого корня на отрезке [-2; -1].

Рисунок 8. Пример решения уравнения при помощи надстройки Поиск решения

Видео:Как найти корни уравнения в Excel с помощью Подбора параметраСкачать

Задание 1. Решение уравнений численным методом

На листе 1 (название листа: Численные методы) для заданного уравнения вида f(x)=0 (Таблица 1. Индивидуальные задания ) реализовать итерационные расчетные схемы методов, указанных в Таблице 1 для нахождения хотя бы одного корня на заданном интервале. Количество итераций просчитать, оценивая , .

Видео:Решение квадратных уравнений. Дискриминант. 8 класс.Скачать

Задания 2. Решение уравнений встроенными средствами “Подбор параметра” и “Поиск решения”

На листе 2 (название листа: Подбор Поиск) для заданного уравнения вида f(x)=0 (Таблица 1. Индивидуальные задания) на заданном интервале и с некоторым шагом (шаг выбрать самостоятельно) построить таблицу значений функции f(x) и определить количество корней уравнения и выделить интервалы, на которых находятся корни. Построить график функции. Уточнить на заданных интервалах с точностью до 10 -6 корни уравнения с помощью встроенных средств: Подбор параметра, Поиск решения

🎥 Видео

Как решают уравнения в России и СШАСкачать

Отделение корней уравнений аналитическим методом. Уточнение корней методом половинного деленияСкачать

Как решить уравнение #россия #сша #америка #уравненияСкачать

5.1 Задача Штурма-ЛиувилляСкачать