Если в уравнение любое из слагаемых перенести из одной части другую при этом (3 видео)

Как репетитор по математике борется с ошибками переноса слагаемых

М не очень часто доводилось исправлять ученические ошибки, казалось бы не поддающихся какому-либо разумному объяснению и анализу. Опытному репетитору по математике хорошо знакомы ситуации, когда дети совершают промахи в казалось бы, в совершенно простых ситуациях. «Как тут можно ошибиться», — спросит начинающий репетитор? Кажется, что выполнить задание правильно куда проще, чем вносить какие-то необъяснимые и нелогичные изменения в записанное.

Профессия «репетитор по математике» — очень сложное ремесло, однако это не должно пугать или оправдывать неудачи. Хороший репетитор находиться в постоянном поиске причин появления ошибок, пробует новые и совершенствует испытанные подходы к их устранению. Как минимизировать частоту появления ошибок?

Рассмотрим типичную проблему при работе репетитора по математике в 6 классе с очень слабым учеником: при решении линейного уравнения школьник хронически ошибается в переносах слагаемых из одной части равенства в другую. Причем страдают не только плюсы с минусами. Пропадают числа, буквы и даже знаки «равно». Ох, чего только я не насмотрелся в ученических тетрадях.

Сами же школьники сетуют на невнимательность, что конечно имеет место быть, но невнимательность часто является следствием появления каких-либо визуальных, звуковых, логических или физических помех при работе.

Как репетитору по математике в 6 классе бороться с ними внутри данной темы? И откуда приходят помехи? Как правило слабый ученик имеет довольно низкие физиологические показатели фиксации внимания на сложном для 6 класса графическом объекте, коим, как это ни странно звучит, является уравнение. В сочетании с параллельно производимой операцией вынужденного переписывания равенства с одновременной его трансформацией, ребенку просто не хватает ресурса контроля за производимыми действиями. Как поступить репетитору по математике в подобной ситуации? Отказаться в 6 классе от переписывания? Я решаю проблему так:

Содержание

Репетитор по математике на карточках
Линейные уравнения. Решение линейных уравнений. Правило переноса слагаемого.
Перенос одной части уравнения в другую правила
Основные приемы решения уравнений.
Уравнения с двумя переменными
Свойства уравнений с двумя переменными:
📹 Видео

Репетитор по математике на карточках

На какой-то период задания должны быть свободны от письма. К нескольким уравнениям, включенным в планы урока, репетитором составляются специальные карточки с изображенными на них слагаемыми. Из них складывается левая и правая часть уравнения и выкладывается перед учеником на стол. На обороте каждой карточки репетитора по математике дублируются эти же слагаемые, но с другими знаками. К примеру, если ребенку нужно перенести 5х из правой части в левую он переносит 5х через знак «=» и переворачивает ее обратной стороной вверх. Получается «- 5х» Такой ход выполнения задания освобождает ребенка от переписывания объекта (уравнения) и позволяет собрать внимание на одной единственной операции, то есть на самом переносе.

Безусловно, репетитору по математике не следует увлекаться карточными играми, ибо все равно нужно вырабатывать умение выполнять действия в процессе письма. Однако на первых порах методика «конструктора ЛЕГО» проявляет большую эффективность, ибо позволяет собрать внимание ученика на главном содержании изучаемой темы. От этого перенос быстрее и лучше запоминается. После того, как ученик проявит уверенность в ответах, репетитор по математике сможет приступить к отработке оформления.

А.Н. Колпаков. Автор подхода — репетитор по математике в Строгино. Москва

Видео:Решение уравнений. Как переносить слагаемые из одной части уравнения в другую. Математика 6 классСкачать

Линейные уравнения. Решение линейных уравнений. Правило переноса слагаемого.

Правило переноса слагаемого.

При решении и преобразовании уравнений зачастую возникает необходимость переноса слагаемого на другую сторону уравнения. Заметим, что слагаемое может иметь как знак «плюс», так и знак «минус». Согласно правилу, перенося слагаемое в другую часть уравнения, нужно изменить знак на противоположный. Кроме того, правило работает и для неравенств.

Примеры переноса слагаемого:

Сначала переносим 5x из левой части уравнения в правую:

Далее переносим (−6) из правой части в левую:

Обратите внимание, что знак «+» изменился на «-», а знак «-» на «+». При этом не имеет значения, переносимое слагаемое число или переменная, либо выражение.

Переносим 1-е слагаемое в правую сторону уравнения. Получаем:

Обратите внимание, что в нашем примере слагаемое — это выражение (−3x 2 (2+7x)). Поэтому нельзя отдельно переносить (−3x 2 ) и (2+7x), так как это составляющие слагаемого. Именно поэтому не переносят (−3x 2 ⋅2) и (7x). Однако мы модем раскрыть скобки и получить 2 слагаемых: (−3x‑⋅2) и (−3×2⋅7x). Эти 2 слагаемых можно переносить отдельно друг от друга.

Таким же образом преобразовывают неравенства:

Собираем каждое число с одной стороны. Получаем:

2-е части уравнения по определению одинаковы, поэтому можем вычитать из обеих частей уравнения одинаковые выражения, и равенство будет оставаться верным. Вычитать нужно выражение, которое в итоге нужно перенести в другую сторону. Тогда по одну сторону знака «=» оно сократится с тем, что было. А по другую сторону равенства выражение, которое мы вычли, появится со знаком «-».

Это правило зачастую используется для решения линейных уравнений. Для решения систем линейных уравнений используются другие методы.

Видео:Виды уравнений. Свойства уравнений. Перенос слагаемых из одной части уравнения в другую. Алгебра 7.Скачать

Перенос одной части уравнения в другую правила

Видео:Вся суть уравнений за 1 секунду. Хватит путать знаки в уравнениях!Скачать

Основные приемы решения уравнений.

1. Перенос слагаемых из одной части уравнения в другую.

Переход от уравнения

f(x) = g(x) + m(x) (1)
к уравнению

f(x) — m(x) = g(x) (2)
называют переносом слагаемых из одной части уравнения в другую.

Перенос слагаемых из одной части уравнения в другую — это преобразование уравнения всегда приводит к равносильному уравнению, т. е., каковы бы ни были функции f(х), m(х), g(x), мы имеем (1)(2).

В самом деле, пусть a — корень уравнения (1), т. е. соотношение

f(a) + m(a) = g(a) = g(a) + m(a) (3)
представляет собой верное числовое равенство. Это означает, что ринадлежит области определения каждой из функций f . слагаемого — х и — 2 получается равносильное уравнение х 4 = х 2 .

Пример 2.
x 2 + lgx = x + lgx х 2 = х. Уравнение x 2 = х имеет корня х₁ = 1, х₂ = 0, тогда как уравнение x 2 + lgx = x + lgx имеет единственный корень х = 1 (число х = 0 не является корнем уравнения x 2 + lgx = x + lgx, так при х = 0 левая и правая части этого уравнения не определены). Таким образом, уравнение х 2 = х не равносильно уравнению х 2 + lgx = x + lgx, а лишь является следствием этого уравнения. Появление постороннего корня х = 0 при переходе от уравнения x 2 + lgx = x + lgx к уравнению х 2 = х связано с тем, что при этом переходе расширяются множества на которых были определены функции, стоящие в левой и правой частях первого уравнения: в уравнении x 2 + lgx = x + lgx левая и правая части определены при х > 0, а в уравнении х 2 = х,при всех х. Очевидно, обратный переход, т. е. переход от уравнения х 2 = х к уравнению х 2 + lg х = х + lgx вообще недопустим, так как этот переход ведет к потере корня х = 0.

Обозначим через М множество, на котором определены функции f(х) и g(x), стоящие в левой и правой частях уравнения f(x) = g(x) (т.е. пересечение областей определения функций f (х) и g(x). Тогда, если множество М содержится в области определения функции m(х), то уравнение f(x) + m(x) — m(x) = g(x) равносильно уравнению f(x) =g(x). При этих условиях f(x) + m(x) = g(x) + m(x)f(x) = g(x).

3. Умножение обеих частей уравнения на одно и то же выражение.

Переход от уравнения

f(x) = g(x) (8)
к уравнению

f(x)p(x) = g(x)p(x). (9)
называют умножением обеих частей уравнения на одно и тоже выражение.

По поводу этого перехода можно высказать следующие утверждения:

1) Если в каждой точке, где определены обе функции f(x), g(x) определена также и функция p(x) (иначе говоря, Если в каждой точке, где определены обе функции f(x), g(x) определена также и функция p(x)), то уравнение (9) является следствием уравнения (8) или (8)(9)

2) Если в каждой точке, где определены обе функции f(x), g(x) определена также и функция p(x) и в каждой точке указанного множества функция p(x) отлична от нуля, то уравнения (8) и (9) равносильны, т. е. (8)(9).

Заметим, что в общем случае переход от уравнения (9) к уравнению (8) может привести как к появлению посторонних корней, так и к потере корней.

Рассмотрим уравнение x 2 — x = 0. Умножив обе части этого уравнения на, мы получим уравнение= 0, которое не является следствием исходного. В самом деле, исходное уравнение имеет корни х₁ = 0, х₂ = 1, а уравнение= 0 — лишь корень х = 1. Потеря корня связана с тем, что функция — не определена при. х = 0, а как раз это значение х является корнем заданного уравнения.

Такой переход применяется довольно часто при решении уравнений. Естественно, возникает вопрос: можно ли утверждать, что уравнение (*) равносильно дизъюнкции уравнений (**)

Иными словами, можно ли получить «множество всех корней уравнения (*), решив все уравнения (**) и объединив их корни? Ответ на этот вопрос дает следующая теорема.

Эта теорема лежит в основе часто применяемого метода разложения уравнения на множители.

Пример 4. x 6 + 3x 5 — x 4 — 3x 3 = 0,

x 3 (x 3 + 3x 2 — x — 3) =0,

x 3 ((x 3 + 3x 2 ) — (x + 3)) =0,

x 3 (x 2 (x + 3) — (x + 3)) =0,

x 3 (x + 3)(x 2 — 1) =0,

x 3 (x + 3)(x — 1)(x + 1) =0.

Уравнение x 6 +3x 5 — x 4 — 3x 3 = 0 равносильно дизъюнкции уравнений x 3 = 0, x + 3 =0, x + 1 = 0, x — 1 = 0 и имеет следующие корни:

Следующий пример показывает, что в общем случае уравнение (*) не равносильно дизъюнкции уравнений (**).

Пример 5. Пусть f₁(х) = х 2 — 1, f₂(х) =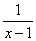. Тогда уравнение f₂(х) = 0 не имеет корней, уравнение f₁(х) = 0 имеет два корня х₁ = 1, х₂ = — 1, а уравнение f₁(х) f₂(х) = 0 имеет только один корень х₁ = -1, так как при х = 1 левая часть этого уравнения не определена.

Теорема 2. Каждый корень уравнения f₁(x)·f₂(x)·. ·f_n(x) = 0 является корнем одного из уравнений f₁(x) = 0, f₂(x) = 0. f_n(x) = 0.

Иначе говоря, дизъюнкция уравнений (**) есть следствие уравнения (*). Из этой теоремы вытекает, что если мы найдем все корни уравнений (**), то среди этих корней будут содержаться все корни уравнения (*) и, быть может, некоторые числа, не являющиеся корнями уравнения (*). Посторонними для уравнения (*) будут те значения х, полученные при решении уравнений (**), для которых хотя бы одна из функций f₁(х), f₂(x), . f_n(x) не определена.

3 а м е ч а н и е. Выше было отмечено, что переход от уравнения
f(x)p(x) = g(x)p(x) к уравнению f(x) = g(x) в общем случае недопустим.

При решении уравнения обычно поступают так. Вместо уравнения
f(x)p(x) = g(x)p(x) рассматривают уравнение (f(x)-g(x))p(x)=0, которое эквивалентно исходному уравнению, т. е. уравнению f(x)p(x) = g(x)p(x).

В свою очередь дизъюнкция уравнений f(x) — g(x) = 0, p(x) = 0 является следствием уравнения (f(x) — g(x))p(x) = 0. Таким образом, если мы решим уравнения f(x) — g(x) = 0, p(x) = 0, а звтем объединим их корни, и проверкой (подстановкой в уравнение (f(x)p(x) = g(x)p(x) отсеем лишние корни, то тем самым мы найдем все корни искомого уравнения.

Пример 6. sinx·ctg2x·arcsin(x — 1)·lg(x — 1) = 0.

Решая каждое уравнение в отдельности, имеем следующее:

sinx = 0, корни этого уравнения x =k, где kZ;

ctg2x = 0, корни этого уравнения: x =+pn, где nZ;

arcsin(x — 1) = 0, корни этого уравнения: x = 1;

lg(x — 1) = 0, корни этого уравнения: x = 2

Те из этих корней, которые принадлежат области определения левой части исходного уравнения, являются корнями исходного урапвнения.

Запишем области определения функций:

M₁ = D(sinx) = (-; +),

M₂ = D(ctg2x) = (-; +), x+m, mZ,

M₄ = D(lg(x — 1)) = (1; +).

Область определения M левой части исходного уравнения является пересечение множеств M₁, M₂, M₃, M₄.
M = (1; )(; 2]. Из всех найденных корней множеству М, т. е. области определения левой части исходного уравнения, принадлежит корень 2. Корнем исходного уравнения является число 2.

5. Переход от уравнения f(x)= g(x) к уравнению [f(х)] n = [g(х)] n . Такой переход нередко используется при решении уравнений, особенно при решении иррациональных уравнений.

Пусть функции f(х) и g(x) определены на множестве М (т. е. множество М содержится в области определения каждой из функций f(x), g(x)) и n — произвольное натуральное число. Будем предполагать, что М — некоторое множество действительных чисел и что на этом множестве функции f (х) и g(x) принимают действительные значения. Мы можем утверждать следующее:

В общем случае переход от уравнения [f(x>] n = [g(x)] n к уравнению f(x) = g(x) не допустим, так как такой переход может привести к потере корней.

Пример 7. Решите уравнение= x + 1.

Решение. Возводя обе части уравнения в квадрат, получим уравнение

2x 2 + 5x — 3 = x 2 + 2x + 1, являющееся следствием уравнения. Полученное уравнение равносильно уравнению х 2 + 3х — 4 = 0, корнями которого являются числа х₁ = -4, х₂ = 1. Проверка показывает, что корень x₁ = — 4 является посторонним для уравнения исходного иррационального уравнения, а корень х₂= 1 удовлетворяет уравнению обоим уравнениям. Таким образом, уравнение исходное заданное уравнение имеет единственный корень х = 1.

Более общим, чем рассмотренный в пятом примере, является переход от уравнения f(x) = g(x) к уравнению m(f(x)) = m(g(x)), где m(t) — некоторая заданная функция. Заметим сразу, что в общем случае такой переход недопустим. В самом деле, пусть Е₁ и Е₂,—множества значений соответственно функций f(x) и g(x) и Е — общая часть (т. е. пересечение) множеств E₁ и Е₂. Если функция m(t) не определена на множестве Е, то уравнение m(f(x)) = m(g(x))не имеет решений, в то время как исходное уравнение могло иметь решения. Если же множество Е содержится в области определения функции m(t), то, как легко доказать, f(x) = g(x)m(f(x)) = m(g(x)). Если же, кроме того, функция m(t) монотонна, то f(x) = g(x) m(f(x) = m(g(x)).

Видео:Решение уравнений ( подобные слагаемые ) . 6 класс .Скачать

Уравнения с двумя переменными

Равенства, содержащие две переменные, называют уравнениями с двумя переменными. Если при изучении уравнений с одной переменной говорят о их корнях, то, имея уравнение с двумя переменными, говорят о парах чисел — его решениях.

Пару значений переменных, обращающую уравнение в верное равенство, называют решением уравнения с двумя переменными.

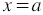
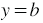
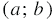
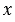
Факт того, что пара чисел , является решением уравнения, условились записывать так: является решением уравнения. При такой записи на первом месте обязательно ставят значение той переменной, которая по алфавиту идет первой, в нашем случае это значение переменной . При этом уравнение с двумя переменными может иметь как бесконечно много решений, так и не иметь не одного.

Решить уравнение с двумя переменными — это значит найти все его решения или показать, что оно не имеет решений.

Свойства уравнений с двумя переменными:

Если к обеим частям данного уравнения прибавить (или из обеих их частей вычесть) одно и то же число, то получим уравнение, имеющее те же решения, что и данное.
Если какое-либо слагаемое перенести из одной части уравнения в другую, изменив при этом его знак на противоположный, то получим уравнение, имеющее те же решения, что и данное.
Если обе части уравнения умножить (разделить) на одно и то же отличное от нуля число, то получим уравнение, имеющее те же решения, что и данное.

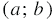
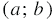
Как говорилось выше решением уравнения с двумя переменными является пара чисел, например , то мы можем изобразить это решение в виде точки М на координатной плоскости. Если мы изобразим все решения уравнения, то получим график уравнения.

Графиком уравнения с двумя переменными называют геометрическую фигуру, состоящую из всех тех, и только тех точек координатной плоскости, координаты которых (пары чисел) являются решениями данного уравнения.

Если какая-то фигура является графиком уравнения, то выполняются два условия:

все решения уравнения являются координатами точек, принадлежащих графику;
координаты любой точки, принадлежащей графику, — это пара чисел, которая является решением данного уравнения.

Поделись с друзьями в социальных сетях: