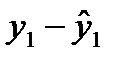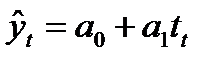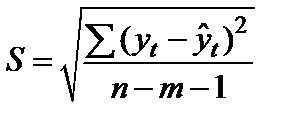Поможем написать любую работу на аналогичную тему
Уравнение тренда представляет собой Y=32,5 – 4,6t. В среднем за год в исследуемом периоде признак изменяется на
Уравнение тренда представляет собой Y=32,5 – 4,6t. В среднем за год в исследуемом периоде признак изменяется на
Уравнение тренда представляет собой Y=32,5 – 4,6t. В среднем за год в исследуемом периоде признак изменяется на
Видео:Лабораторная работа Прогнозирование по уравнению трендаСкачать
Компоненты временного ряда
ТЕМА 5. МЕТОДЫ АНАЛИЗА ВРЕМЕННЫХ РЯДОВ
Лекция 9. Компоненты временного ряда. Модели тренда. Индексы сезонности.
Основная цель анализа временных рядов – прогнозирование будущего состояния объекта (процесса), получение базовой информации для принятия управленческих решений. Для реализации прогноза необходима модель, адекватно описывающая поведение ряда. Выбор конкретной модели определяется характером изменения уровней ряда, присутствием тех или иных компонент.
Компоненты временного ряда
Уровни рядов динамики формируются под влиянием множества факторов. Одни из них действуют стабильно на протяжении длительного периода времени и формируют основную тенденцию временного ряда, которая называется трендом.
Ряд факторов влияют на уровни ряда с определенной периодичностью, циклически (экономические циклы, циклы солнечной активности и т.п.). Для обнаружения и анализа влияния циклических факторов необходимы достаточно длинные временные ряды.
Повторяющиеся колебания уровней внутри года – результат влияния сезонных факторов.
Влияние случайных факторов на уровни ряда происходит без какой-либо периодичности, и, следовательно, не поддается измерению.
Исходя из вышесказанного, уровень временного ряда может быть представлен как функция четырех компонент:
,(9.1)
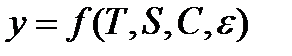
где T – трендовая компонента; S – сезонная компонента; C – циклическая компонента;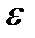 
– случайная компонента.
Чем сильнее влияние не трендовых компонент, тем сложнее выявить и описать основную тенденцию ряда, а именно это является центральной задачей при построении моделей временных рядов.
Сгладить влияние на уровни ряда не трендовых компонент позволяет процедура выравнивания временных рядов. Суть этой процедурысостоит в замене фактических уровней изучаемого ряда теоретическими. Теоретические уровни –это уровни, в той или иной мере очищенные от влиянияне трендовых компонент и полученные врезультате определенных расчетов, преобразований исходного ряда.
В арсенале статистикидва приема выравнивания временных рядов: механическое выравнивание и аналитическое.
Механическое выравнивание может быть осуществлено:
« Методом укрупнения интервалов. Данный метод предполагает объединение временных периодов и расчет по ним либо суммарных значений показателей, либо средних величин. Например, если ряд был представлен данными по месяцам, то выравнивание будет заключаться в объединении уровней и представлении ряда данными по кварталам. Укрупнение временных интервалов приведет к снижению степени колеблемости уровней и к более отчетливому проявлению тенденции.
« Метод скользящей средней.Данный метод предполагает расчет среднего уровня за определенный временной интервал (например, 3-5 лет), и дальнейшее скольжение интервала по временному ряду (напомним, что в средних величинах происходит взаимопогашение влияния случайных факторов). Полученные средние (выровненные) значения уровней относятся к середине интервала, по которому рассчитываются средние. Так, если период скольжения три года, первая средняя величина будет рассчитана:
, а полученное среднее значение будет отнесено ко второму периоду. Далее рассчитывается средняя величина следующих 3-х уровней:
, полученное значение будет отнесено к третьему периоду ряда и т.д.
Если период скольжения – четная величина, то применяют метод центрирования. Этот прием выражается в подсчете средней арифметической величины из значений, полученных по двум шагам скольжения.
Увеличение периода скольжения позволяет более отчетливо проявиться основной тенденции, однако результатом является существенно укороченный временной ряд, что неблагоприятно может сказаться на качестве трендовой модели.
Аналитическое выравнивание позволяет не только выявить основную тенденцию ряда, но и получить аналитическую форму тренда в виде уравнения.
Уравнение (модель) тренда – это парное уравнение регрессии, в качестве фактора в котором выступает время (t).Переменная «t» задается простой последовательностью чисел от 1 до n. В общем виде уравнение может быть записано:
, (9.2)
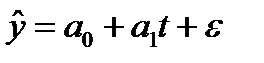
где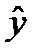 
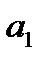
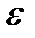
– зависимая переменная, условное среднее значение уровней временного ряда; 
и 
– параметры уравнения тренда; t– независимая переменная, фактор-время; 
— случайная составляющая.
Расчет параметров трендовой модели осуществляется с использованием метода наименьших квадратов (о котором говорилось в теме регрессионного анализа).
Центральной проблемой построения трендовой модели является выбор типа уравнения тренда, наилучшим образом описывающего основную тенденцию изучаемого ряда. Для решения этой задачи могут быть использованы:
· графическое представление временного ряда;
· метод конечных разностей;
· формализованный подход, т.е. метод критериев.
При графическом представлении временных рядов по оси абсцисс откладываются периоды или моменты времени, по оси ординат – значения уровней ряда. Расположение эмпирической линии тренда на графике позволяет выдвинуть гипотезу о типе уравнения тренда.
Метод конечных разностей основан на свойствах математических функций и анализе показателей изменения уровней временных рядов. Так, если примерно постоянными являются первые разности (абсолютные приросты), для описания тренда можно воспользоваться полиномом первой степени (линейной функцией). Если примерно постоянны вторые разности (показатели ускорения), то следует использовать полином второй степени и т.д.
В настоящее время выбор функции, для описания тренда, как правило, формализован, т.е. осуществляется с использованием статистических критериев на базе пакетов прикладных программ. Аналитик одновременно строит несколько уравнений тренда, а затем, исходя из значений определенных критериев, выбирает одно, дающее лучшую аппроксимацию.
В качестве критериев выбора модели тренда могут быть использованы следующие характеристики:
1. Минимальная сумма квадратов отклонений теоретических значений уровней ряда (полученных на основе уравнения тренда) от фактических:
, (9.3)
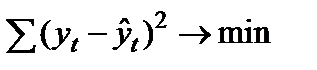
где yt– фактическое значение уровня ряда периода t; 
— теоретическое значение уровень ряда периода t.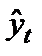
2. Минимальная величина остаточной дисперсии (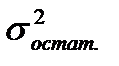 
) 
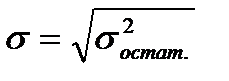
или минимальное значение среднеквадратической ошибки уравнения тренда 
.
3. Минимальное значение средней ошибки аппроксимации:
. (9.4)
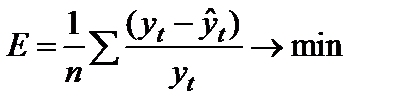
4. Максимальное значение F-критерия Фишера, оценивающего значимость уравнения в целом (см. тему регрессионного анализа):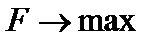 
.
5. Максимальное значение коэффициента детерминации, характеризующего долю объясненной дисперсии в общей дисперсии результативного признака: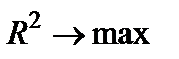 
.
Продолжая анализировать динамику показателя обеспеченности жильем, построим три уравнения тренда, используя линейную функцию, параболу второго порядка и экспоненту. Результаты расчетов, выполненных в пакете STATISTICA, представлены в таблицах 9.1, 9.2, 9.3 (структура и анализ таблиц трендовых моделей аналогичны таблицам парных уравнений регрессии.См. соответствующую лекцию.).
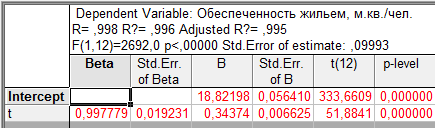
Таблица 9.1 — Линейный тренд временного ряда показателей общей площади жилых помещений, приходящейся в среднем на одного жителя, м.кв./чел.
Графа «В» таблицы содержит значения параметров уравнения, t- статистика позволяет оценить статистическую значимость параметров модели. В верхней части таблицы приведены значения коэффициента корреляции (R), коэффициента детерминации (R?=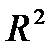 
), скорректированного коэффициента детерминации (AdjustedR?) и F — критерия Фишера (F).
Уравнение может быть записано: y = 18,82 + 0,34 t.
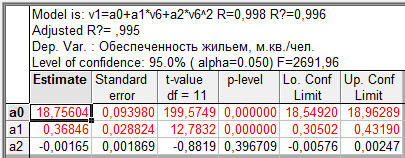
Таблица 9.2 — Параболический тренд временного ряда показателей общей жилой площади, приходящейся в среднем на одного жителя, м.кв./чел.
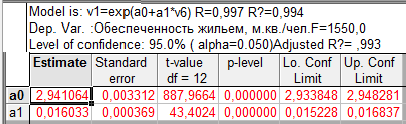
Расчет характеристик, содержащихся в таблицах 9.2 и 9.3, выполнен в процедуре нелинейного оценивания программыSTATISTICA, в этих таблицах значения параметров уравнения находятся в графе Estimate, в двух последних графах дополнительно приводятся значения границ доверительных интервалов для генеральных параметров.
Таблица 9.3 — Экспоненциальный тренд временного ряда показателей общей жилой площади, приходящейся в среднем на одного жителя, м.кв./чел.
Для анализа результатов расчетов и выбора модели тренда построим сводную таблицу 9.4.
Таблица 9.4 — Оценка статистической значимости параметров и уравнений тренда
| Уравнение тренда |  |  |  |  |  |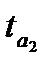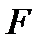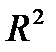
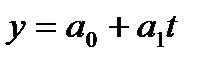 | 333,66 | 51,88 | — | 2692,0 | 0,995 |
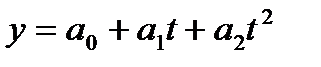 | 199,58 | 12,78 | 0,88 | 2691,96 | 0,995 |
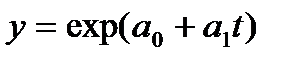 | 887,97 | 43,40 | — | 1550,0 | 0,994 |
Параметры линейной и экспоненциальной моделей статистически значимы, поскольку расчетное значение t — статистики для каждого параметра больше табличного значения t — статистики с учетом принятого уровня значимости и соответствующего числа степеней свободы ( 
(0,05; 12)=2,179). Расчетные значения F — критерия, также превышающие табличное значение ( 
(1,12)=4,75), следовательно, уравнения в целом и значения коэффициента детерминации статистически значимы, т.е. данные модели позволяют объяснить существенную часть вариации зависимой переменной — показателя обеспеченности жильем населения России.
В уравнении полинома второго порядка параметр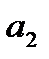 
статистически не значим, поскольку 
(0,88) (2,11)=3,98), оно не может быть использовано для прогнозирования значений зависимой переменной.
Выбор между двумя статистически значимыми уравнениями осуществляется на основе значений коэффициентов детерминации, характеризующих долю объясненной дисперсии в общей дисперсии зависимой переменной. Предпочтение следует отдать линейной модели, которой соответствует большее значение коэффициента детерминации ( 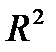=0,995).
Уравнение тренда может бытьпризнано моделью, пригодной для прогнозирования, если оно отвечает следующим требованиям:
· уравнение в целом статистически значимо (оценка по F-критерию);
· все параметры уравнения статистически значимы (оценка по t-статистике);
· в остатках уравнения отсутствует автокорреляция.
Процедуры оценки статистической значимости уравнения в целом и его параметров подробно рассмотрены в разделе КРА. Остановимся на оценке автокорреляции в остатках модели.
Остатки– это разность между фактическими значениями уровней временного ряда и выровненными (теоретическими) значениями, полученными по уравнению тренда.
Фактические уровни: Теоретические
(выровненные) уровни: Остатки:
y1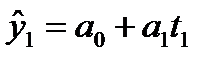 
y2 
y3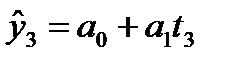 
…… ………………………. ……………..
yt 
Рисунок 9.1 — Определение величины остатков модели временного ряда
Автокорреляция остатков – это зависимость остатков периода t от остатков предшествующих периодов (t-i). Если построенное уравнение обеспечивает удовлетворительную аппроксимацию, то отклонения от тренда (остатки) должны носить случайный характер и в их последовательности не должно быть корреляции.
Исследование автокорреляции остатков трендовой модели имеет особое значение, если ставится задача прогнозирования поведения временного ряда. Дело в том, что наличие автокорреляции свидетельствует о наличии тенденции в остатках, т.е. о сохранении в них части полезной информации. Поскольку основная задача построения трендовой модели – как можно более полно описать основную тенденцию изучаемого ряда – сохранение тенденции в остатках, говорит о том, что модель не может быть признана пригодной для получения прогнозаудовлетворительногокачества.
Оценка автокорреляции в остатках может быть проведена на основе коэффициентов автокорреляции, либо с использованием специального критерия — критерияДарбина-Уотсона.
Если остатки периода t обозначить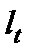 
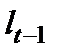
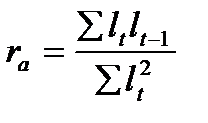
, а остатки предшествующего периода 
, то коэффициент автокорреляции, предложенный М. Езекиэлом и К. Фоксом, будет рассчитываться:
. (9.5)
Коэффициент автокорреляции изменяется в пределах: 
, как и обычный парный коэффициент корреляции. Близость значения коэффициента к нулю означает отсутствие автокорреляции, к единице – наличие автокорреляции в остатках.
По достаточно большим временным рядам могут быть рассчитаны коэффициенты автокорреляции разных порядков, т.е. коэффициенты, оценивающие зависимость не только между остатками соседних периодов, но между остатками, разделенными двумя, тремя и большим числом временных интервалов. Интервал, разделяющий зависимые остатки, называют лагом. Величина лага определяет порядок коэффициента автокорреляции. Последовательность коэффициентов автокорреляции разного порядка называется автокорреляционной функцией, которая характеризует зависимость величины коэффициентов автокорреляции от величины лага.
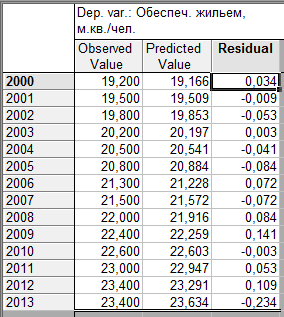
В таблице 9.5 приведены фактические (ObservedValue), теоретические (PredictedValue), т.е. рассчитанные по линейной модели, значения показателя обеспеченности жильем и величины остатков (Residual), равные разности значений двух первых столбцов.
Таблица 9.5 — Фактические, теоретические уровни и остатки линейного тренда временного ряда показателей общей жилой площади, приходящейся в среднем на одного жителя, м.кв./чел.
Для оценки автокорреляции остатков рассчитаем коэффициенты автокорреляции. Поскольку анализируемый временной ряд содержит всего 14 уровней, то рассчитаем коэффициенты лишь трех порядков: первого, который покажет степень корреляционной зависимости между смежными значениями остатков; второго, т.е. будет дана оценка зависимости между остатками, разделенными двумя годами; третьего порядка — оценка корреляционной связи между остатками с интервалом в три года.
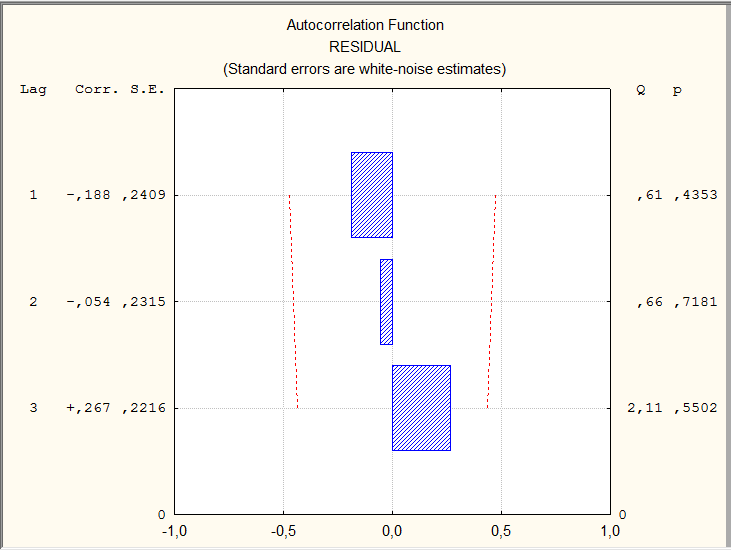
Автокорреляционная функция остатков линейной модели и ее графическое отображение представлены на рисунке 9.2.
Рисунок 9.2 — Автокорреляционная функция остатков линейной модели временного ряда показателей общей жилой площади, приходящейся в среднем на одного жителя, м.кв./чел.
Графическое отображение коэффициентов автокорреляции (прямоугольники) сопровождается числовыми значениями этих характеристик (графа Corr.): коэффициент автокорреляции первого порядка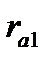 
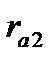
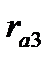
= — 0,188, второго 
= -0,054, третьего 
=0,267. На порядок коэффициентов автокорреляции указывает величина лага (Lag). Статистическую значимость коэффициентов можно оценить, рассчитав t — статистику:
(9.6)
где: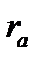 
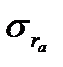
– коэффициент автокорреляции, 
— стандартная ошибка коэффициента автокорреляции (графаS.E.).
В результате расчетов получены следующие величины t — статистики: 
=0,78, 
=0,23 и 
=1,2. Все значения t — статистики не превышают табличного значения ( (0,05)=2,179), которое находится по таблице распределения Стьюдента, поскольку объем данных менее 30. Таким образом, полученные значения коэффициентов автокорреляции статистически не значимы. Проведенная оценкаговорит об отсутствии автокорреляции в остатках линейной модели тренда. Этот вывод подтверждается и графическим представлением автокорреляционной функции: величины коэффициентов, представленные прямоугольниками, не выходят за пределы доверительных интервалов, обозначенных пунктирными линиями.
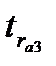
Рассмотрим еще один метод оценки автокорреляции в остатках — критерий Дарбина-Уотсона (D-W). Используя введенные ранее обозначения (см. 9.5), критерий может быть рассчитан следующим образом:
. (9.10)
Между критерием Дарбина-Уотсона и коэффициентом автокорреляции существует следующее соотношение: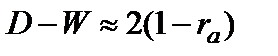 
.
Исходя из этого соотношения, очевидно, что если:
Таким образом, значение критерия может изменяться в пределах:
. (9.11)
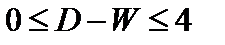
Близость D-W к 0 и к 4 означает присутствие автокорреляции в остатках, к 2 – ее отсутствие.
КритерийДарбина-Уотсона табулирован. По таблицам, исходя из числа уровней динамического ряда и числа факторов в уравнении тренда, находят границы значения критерия: 
, 
— нижняя и верхняя границы критерия.
— автокорреляция в остатках присутствует;
— автокорреляция в остатках отсутствует;
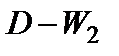
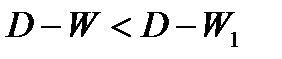
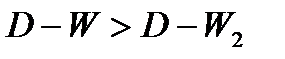
Если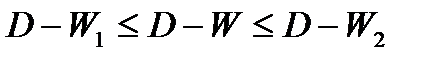 
— возникает ситуация неопределенности, которая требует дальнейшего исследования ряда в условиях увеличения объема данных, или использования иного типа модели.
Оценивая остатки линейной модели рассматриваемого примера, в программе STATISTICA было получено значение критерия Дарбина-Уотсона=1,91. Табличные значения верхней и нижней границ критерия (см. приложение . )следующие: = 1,05, =1,35. Поскольку расчетное значение критерия (1,91) превышает верхнюю границу табличного значения (1,35), подтверждается вывод об отсутствии автокорреляции в остатках модели тренда временного ряда показателей общей жилой площади, приходящейся в среднем на одного жителя, м.кв./чел.
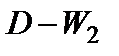
Таким образом, весь комплекс требований, необходимых для признания модели тренда пригодной для прогнозирования, выполнен: уравнение тренда статистически значимо, параметры статистически значимы, в остатках модели отсутствует автокорреляция.
Регрессионную модель тренда, отвечающую всем формальным требованиям, можно использовать для оценки величины переменной y в последующие периоды времени t. Чтобы получить, так называемый, точечный прогноз при заданном значении t, вычисляется значение построенной функции регрессии в точке t.
В рассматриваемом примере исходный временной ряд включал 14 уровней (данные с 2000 по 2013 годы), следовательно, точечный прогноз может быть выполнен на 15-й период(на 2014 год) и дальнейшие периоды. Подставляя в уравнение значение t=15 (y=18,82 + 0,34*15), получаем, что прогнозируемое среднее значение показателя обеспеченности жильем в России в 2014 году составит 23,92 м.кв./чел.
Однако следует помнить, что уравнение тренда описывает лишь общую тенденцию изменения показателя. Фактическая реализация событий отличается от прогнозируемой. Совпадение фактических и прогнозных значений маловероятно. Уравнение тренда всегда содержит ошибку, которую принято оценивать среднеквадратической (стандартной) ошибкой тренда:
где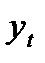 
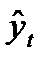
— фактическое значение уровня ряда периода t; 
— значение уровня ряда периода t, рассчитанное по уравнению тренда; n – число уровней ряда; m – число факторов, включенных в уравнение;n-m-1 –число степеней свободы остаточной дисперсии.
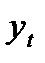
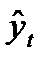
Как видим, средняя ошибка тренда – это корень квадратный из остаточной дисперсии, которая оценивает степень колеблемости уровней временного ряда ( ) относительно тренда ( ). Среднеквадратическая ошибка тренда, таким образом, характеризует: насколько в среднем отличаются значения уровней ряда, рассчитанные на основе уравнения, от их фактических значений.
С учетом ошибки тренда может быть рассчитан доверительный интервал прогноза:
(9.13)
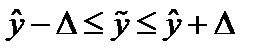
где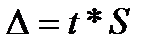 
—предельная ошибка;t – коэффициент доверия, величина которого находится по таблице Стьюдента, исходя из принятого исследователем уровня значимости и соответствующего числа степеней свободы (n-m-1).
При выполнении расчетов с использованием специализированных компьютерных программ, величина ошибки определяется в одной процедуре с расчетом значений параметров уравнения. В таблице 9.1 представлено значение стандартной ошибка линейного тренда (St.Errorofesimate): S=0,0999. Величина коэффициента доверия, исходя из уровня значимости 0,05 и числа степеней свободы 12 (14-1-1), равна 2,179 (см. прил. Табл. Стьюд.), тогда
2,179 * 0,0999 = 0,218. Доверительный интервал будет рассчитан: 
и окончательно — 
. Таким образом, с вероятностью 0,95 можно утверждать, что в среднем показатель обеспеченности жильем в регионах России в 2014 году будет не ниже 23,7 и не выше 24,14 квадратных метров на человека (заметим, что фактическое значение показателя в 2014 году по данным Росстата составило 23,7 квадратных метра на человека).
Прогнозирование на основе временных рядов называют экстраполяцией — продлением в будущее тенденции, сложившейся в прошлом. Следовательно, доверять результатам прогнозирования можно при условии, что факторы, повлиявшие на формирование тенденции в прошлом, неизменно будут действовать и в будущем. Еще один практический совет, выработанный статистикой: период упреждения, т.е. период на который делается прогноз, не должен превышать 1/3 длины ряда, на основе которого построена модель.
Видео:Прогнозирование в Excel с помощью линий трендаСкачать
Ответы на тесты по теме Статистика
Для более эффективного поиска следует вводить 2-3 ключевых слова из вопроса .
уравнение тренда имеет вид у = 66,61+7,57 t на сколько в среднемежегодно изменялся анализируемый показатель
увеличивался на 7,57
Остатки модели тренда — это
разность между фактическим и теоретическим значениями уровней ряда
Остатки модели тренда – это
продлением в будущее.
—> для выравнивания временного ряда характеризующего изменение количества машин в автопарке за ряд лет, использовано уравнение тренда вида Y=a+bt. Параметр b характеризует
срдний годовой абсолютный прирост
при прогнозировании на основе уравнения тренда в качестве значения независимой переменной используется
порядковый номер периода на который.
по данным о динамике ВВП России за 11 лет (в млрд дол по ППС) получено уравнение тренда y=1815,41+167,95t чему равен прогноз объема ВВП по уравнению на следуюзий период
3662,86( не правильно) 3830,81
прогнозирование на основе урвнения тренда возможно, если
выполняются все перечисленные условия
при каком из ниже приведенных значений t что параметр модели тренда значим
Задача. На основе временного ряда показателей оборота малых предприятий в России за период с 2009 по 2014 годы получена модель тренда: y=15958,27+1815,40*t Величина стандартной ошибки оценивания — 810. 12 млрд.руб.
28666,07 млрд. руб
По данным о динамике ВВП США в период с 2000 по 2014 года построена линейная модель тренда: y=9806,37+498,84*t
Значение x x x 353,93
Задача. По данным о динамике ВВП США в период с 2000 по 2014 годы построена линейная модель тренда y=9806.37 + 498.84 * t и получены значения характеристик (192,31 21,15 69675677 125265)
Значение X X 556,23 X
Для выравнивания временного ряда, характеризующего изменение количества машин в автопарке за ряд лет, использовано уравнение тренда вида: Y=a+bt. Параметр b характеризует
средний годовой абсолютный прирост
выполняются все перечисленные условия
Для выравнивания временного ряда, характеризующего изменение количества машин в автопарке за ряд лет, использовано уравнение тренда вида: Y=a+bt. Параметр b характеризует:
средний годовой абсолютный прирост
При каком из ниже приведенных значений t — статистики можно утверждать, что параметр модели тренда статистически значим:
Остатки модели тренда – это:
разность между фактическими и теоретическими значениями уровней ряда
По данным о динамике ВВП России за 11 лет (в млрд. дол. по ППС) получено уравнение тренда: yt=1815,41+167,95t. Чему равен прогноз объема ВВП по уравнению на следующий период
По данным о динамики ВВП США в период с 2000 по 2014 годы построена линейная модель тренда: и получены значения характеристик:
Задача. На основе временного ряда показателей оборота малых предприятий в России за период с 2009 по 2014 годы получена модель тренда:
Видео:Быстрое прогнозирование в Microsoft ExcelСкачать
Лабораторная работа №6. Анализ динамических рядов
Лабораторная работа №6. Анализ динамических рядов
При исследовании многих природных и производственных процессов возникает задача анализа в динамике событий и их последовательностей, которые не поддаются методам стандартного математического анализа, поскольку зависят от случайных факторов. Основными задачами в таких исследованиях являются детальное изучение этих процессов, выделение их существенных характеристик, которое может привести к возможности прогнозирования развития этих процессов в будущем. Также представляет интерес выделение внутренних закономерностей, которым подчинено развитие этих процессов.
Временной ряд (динамический ряд, ряд динамики) – это последовательно измеренные через некоторые промежутки времени данные о значении какого-либо параметра исследуемого процесса (или нескольких параметров, в этом случае говорят о многомерном временном ряде).
Временной ряд состоит из двух элементов:
— периода времени, за который или по состоянию на который приводятся числовые значения;
— числовых значений показателя, называемых уровнями ряда.
Временные ряды бывают детерминированными (получены на основе значений некоторой неслучайной функции, например, ряд последовательных данных о количестве дней в месяцах) и случайными (результат реализации некоторой случайной величины).
Классификация временных рядов проводится по следующим признакам.
• По характеру показателя, для которого определяются уровни:
— детерминированные ряды, которые получены на основе значений некоторой неслучайной функции, например, ряд последовательных данных о количестве дней в месяцах;
— случайные ряды, представляющие собой реализацию некоторой случайной величины.
• По форме представления уровней:
— ряды абсолютных величин;
— ряды средних величин.
• По характеру временного показателя:
— моментные ряды, в которых уровни характеризуют значение показателя по состоянию на определенные моменты времени;
— интервальные ряды, уровни которых характеризуют значение показателя за определенные периоды времени. Важная особенность интервальных временных рядов абсолютных величин заключается в возможности суммирования их уровней.
• По расстоянию между датами и интервалами времени:
— полные или равноотстоящие ряды, если даты регистрации или окончания периодов следуют друг за другом с равными интервалами;
— неполные или неравноотстоящие ряды, если принцип равных интервалов не соблюдается или имеются пропущенные значения.
При изучении рядов динамики обычно решают следующие задачи:
1. Вычислить числовые и функциональные характеристики ряда (описательные методы).
2. Определить, имеется ли некоторая неслучайная, закономерная компонента, описывающая тенденцию (тренд) процесса.
3. Определить, нет ли регулярных, колебательных “сезонных” компонент, которые связаны с периодическими естественными колебаниями параметров случайного процесса.
4. Выделить и описать основные колебания случайного процесса вокруг тренда, в случае необходимости удалить влияние второстепенных факторов.
5. Дать прогноз развития случайной процесса на ближайшее будущее и указать степень уверенности в этом прогнозе.
Следует иметь в виду, что при изучении рядов динамики необходимо соблюдение ряда условий:
• Статистические данные должны быть сопоставимы по территории, кругу охватываемых объектов, единицам измерения, времени регистрации, ценам, методологии расчета. Сопоставимость по территории означает, что данные по странам и регионам, границы которых изменились, должны быть пересчитаны в старых пределах. Сопоставимость по кругу охватываемых объектов означает сравнение совокупностей с равным числом элементов. Сопоставимость обеспечивается так называемым смыканием рядов динамики. При этом абсолютные уровни могут заменяться относительными, иногда делают пересчет в условные абсолютные уровни и т. п.
• Числовые уровни рядов динамики должны быть упорядоченными во времени. Не допускается анализ рядов с пропусками отдельных уровней (неполных динамических рядов), если же такие пропуски неизбежны, то их восполняют условными расчетными значениями.
• Временные ряды применяются только для краткосрочного прогнозирования (чаще всего на 1 период вперед).
• Для анализа и прогноза необходима достоверная информация о развитии исследуемого явления минимум за пять периодов.
Числовые характеристики динамических рядов
• Интенсивность изменений уровней ряда во времени характеризуют аналитические показатели. Различают базисные (изменение относительно начального уровня ряда) и цепные (изменение относительно предыдущего уровня) показатели:
Табл.6.1. Аналитические показатели ряда динамики
Абсолютный прирост Di
Коэффициент роста Кр
Коэффициент прироста Кпр
Темп прироста Тпр
Абсолютное значение одного процента прироста А
• Ряд динамики в целом характеризуют средние показатели:
Средний уровень ряда:
— для полного интервального ряда абсолютных величин:
;
— для полного интервального ряда относительных и средних величин средний уровень должен определяться с учетом информации, связанной с осредняемым:
, если 
— соответствующая абсолютная величина;
— для моментного динамического ряда:
;
в частности, для полного моментного ряда:
.
Средний абсолютный прирост:
.
Средний коэффициент (темп) роста:
.
Средний коэффициент (темп) прироста:
, 
.
Пример 6.1. Имеются данные о числе пожаров (тыс. случаев) в России в 1974-1988 гг. Вычислить характеристики динамического ряда.
Решение. Прежде всего классифицируем данный динамический ряд: это полный интервальный ряд абсолютных величин.
Перенесем данные в Еxcel, расположив их в два столбца. Добавим также столбец «№ периода», начиная с 0.
Для аналитических показателей подготовим две таблицы – для базисных и цепных показателей, по периодам начиная с 1, и вычислим соответствующие показатели в таблице по формулам в таблице 6.1, результат будет выглядеть так:
Вычислим теперь средние показатели.
Поскольку мы имеем дело с полным интервальным рядом абсолютных величин, средний уровень ряда вычисляем по самой простой формуле среднего арифметического уровней, используя функцию СРЗНАЧ:
Средний абсолютный прирост также вычислить просто:
Для вычисления среднего коэффициента роста воспользуемся функцией ПРОИЗВЕД, а для извлечения корня применим возведение в степень 1/n:
Анализ тренда динамического ряда
Перейдем теперь к задачам собственно анализа временного ряда и прогнозирования.
В общем виде временной ряд представляют, в зависимости от задачи, в виде аддитивной (6.1) или мультипликативной (6.2) модели, на основании которой дается прогноз:
(6.1)
(6.2)
где 
— детерминированная составляющая, 
— стохастическая (случайная) составляющая.
В детерминированную составляющую могут входить три элемента:
— эволюционная составляющая — характеризует основную тенденцию развития исследуемого объекта (тренд)
— сезонная составляющая — показывает колебания показателя в течение года.
— циклическая составляющая — формируется под воздействием долговременных циклических факторов
Стохастическая составляющая формируется под воздействием большого числа случайных факторов, не отражаемых в прогнозной модели.
Выделение тренда может быть произведено тремя методами:
1. Укрупнение интервалов. Ряд динамики разделяют на некоторое достаточно большое число равных интервалов. Если средние уровни по интервалам не позволяют увидеть тенденцию развития явления, переходят к расчету уровней за большие промежутки времени, увеличивая длину каждого интервала (одновременно уменьшается количество интервалов).
2. Метод скользящей средней. В этом методе исходные уровни ряда заменяются средними величинами, которые получают из данного уровня и нескольких симметрично его окружающих. Целое число уровней, по которым рассчитывается среднее значение, называют интервалом (окном) сглаживания. Интервал может быть нечетным (3, 5, 7 и т. д. точек) или четным (2, 4, 6 и т. д. точек).
При нечетном сглаживании полученное среднее арифметическое значение закрепляют за серединой расчетного интервала.
При четном сглаживании:
— определяют нецентрированные скользящие средние по четному числу уровней,
— вычисляют центрированные скользящие средние как смежные парные средние нецентрированных скользящих средних и относят их к соответствующим периодам или моментам времени.
3. Аналитическое выравнивание. Под этим понимают построение уравнения регрессии
.
Вид уравнения регрессии выбирают так, чтобы оно давало содержательное объяснение изучаемого процесса; основываясь на характере изменения цепных темпов роста, чаще всего выбирают линейную, параболическую, экспоненциальную зависимость или линеаризуемые функции (полулогарифмическую, степенную, гиперболы). Следует помнить, что для достаточной надежности уравнения тренда, как правило, на каждый параметр должно иметься 6-7 моментов или интервалов. Но анализ длинных рядов динамики не всегда возможен, поскольку основная тенденция ряда могла изменяться из-за каких-то внешних причин. Поэтому предпочтение отдается функциям с малым числом параметров
Методы выравнивания можно комбинировать, например, построив уравнение регрессии по уровням, сглаженным методом скользящей средней. Обычно это делают для выявления сезонности, выбирая окно сглаживания равным периоду предполагаемой сезонности (например, год для выявления внутригодичной сезонности).
При аналитическом выравнивании обычно данные временные моменты (например, годы) заменяют на условные моменты времени (например, 1,2,… или 0,1,2…). Кроме того, для простоты вычислений часто условные моменты выбирают так, чтобы их сумма была равна 0 (например, -5,-4,-3,-2,-1,0,1,2,3,4,5)
В Excel аналитическое выделение тренда осуществляется теми же методами, что и построение уравнения регрессии в корреляционно-регрессионном анализе.
Выбор наилучшего уравнения тренда осуществляется по следующим критериям:
• Чем больше значение коэффициента детерминации R2, тем точнее уравнение тренда описывает вариацию уровней динамического ряда. Влияние случайного фактора оценивается как (1-R2)
• Чем больше величина F-критерия, тем предпочтительнее данное уравнение тренда. Если значение F-критерия меньше критического, то уравнение не пригодно для описания тренда и прогнозирования
• Существует (и реализовано в различных статистических пакетах) множество методик анализа остатков 
на случайность. Неслучайность остатков означает либо что выбрано неподходящее уравнение тренда, либо что ряд имеет периодичности, которые затем выявляют специальными методами анализа.
Один из способов визуальной проверки качества уравнения регрессии заключается в анализе графиков остатков.
Другой способ предоставляет критерий Дарбина-Уотсона DW, позволяющий оценить автокорреляцию остатков:
.
При заданном уровне значимости, числе уровней динамического ряда и числе параметров при t в уравнении тренда находят табличные критические значения критерия.
Если ral>0 , то при DW DW2 нет автокорреляции остатков, уравнение можно использовать.
📽️ Видео
Удалили с экзамена ОГЭ Устное Собеседование shorts #shortsСкачать
Парная регрессия: линейная зависимостьСкачать
Самая ЛУЧШАЯ СТРАТЕГИЯ Для Определения СМЕНЫ ТРЕНДА! Обучение ВОЛНОВОМУ АНАЛИЗУ!Скачать
Основы трейдинга: шесть признаков разворота трендаСкачать
Как определить разворот тренда на бирже? Признаки разворота тренда на графике. ТрейдингСкачать
Excel для полных чайников Урок 16 Линия трендаСкачать
Решение тригонометрических уравнений. Подготовка к ЕГЭ | Математика TutorOnlineСкачать
Почти никто не решил ➜ Найдите сторону треугольникаСкачать
Как торговать по линиям тренда | Фишки + примеры сделокСкачать
Линии тренда. Как построить линии тренда. Что такое линия тренда.Скачать
Как проверяют учеников перед ЕНТСкачать
Расчет коэффициента корреляции в ExcelСкачать
Эконометрика. Моделирование временных рядов. Построение аддитивной модели.Скачать
Почему никто не стареет? | Тренд на вечную молодость зашел слишком далеко...Скачать
Простой прогноз продаж в Excel с учетом сезонностиСкачать
Явные признаки начала ТРЕНДА/БОКОВИКА. Трейдинг. Прогноз РЫНКА от В.Гаевского и К.ЦарихинаСкачать
Временные ряды и прогнозированиеСкачать
