О чем эта статья:
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Видео:Решение квадратных уравнений. Дискриминант. 8 класс.Скачать

Определение квадратного неравенства
Неравенство — алгебраическое выражение, в котором используются знаки ≠, , ≤, ≥.
Числовое неравенство — это такое неравенство, в записи которого по обе стороны от знака находятся числа или числовые выражения.
Решение — значение переменной, при котором неравенство становится верным.
Решить неравенство значит найти множество, для которых оно выполняется.
Квадратное неравенство выглядит так:
 |
где x — переменная,
Квадратное неравенство можно решить двумя способами:
- графический метод;
- метод интервалов.
Видео:Решение квадратных неравенств | МатематикаСкачать

Решение неравенства графическим методом
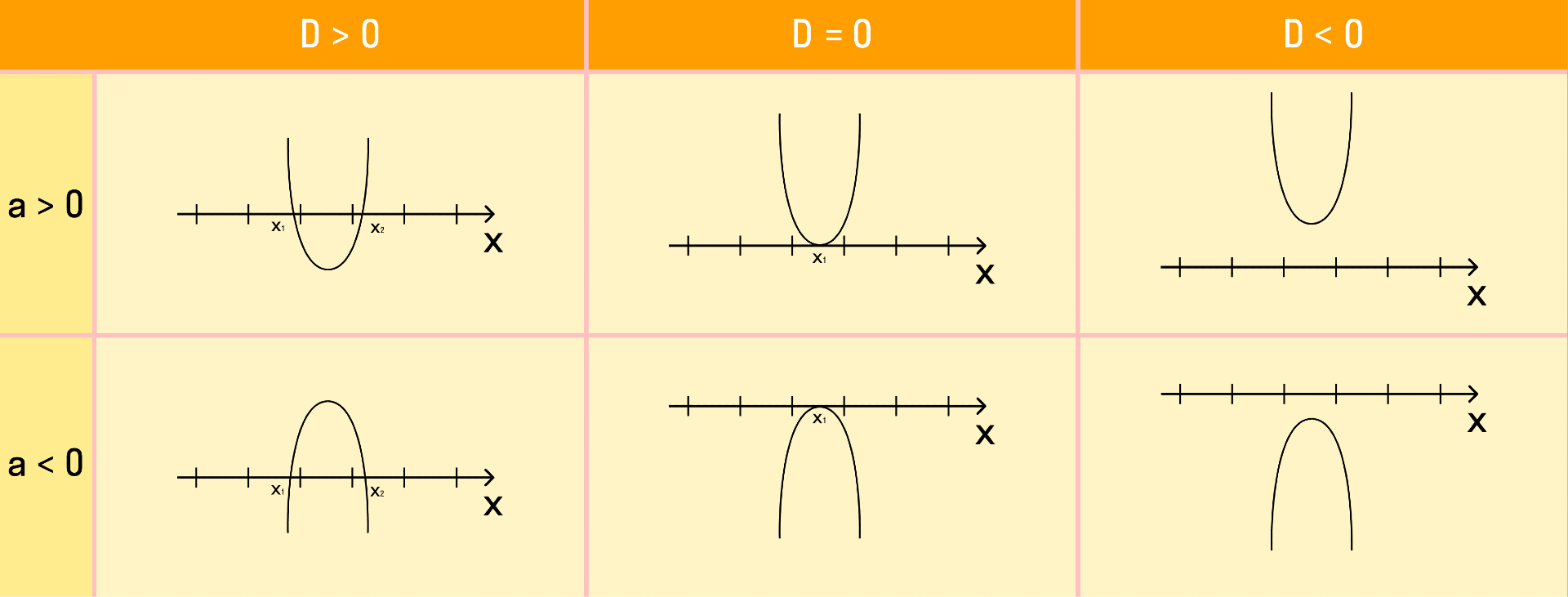
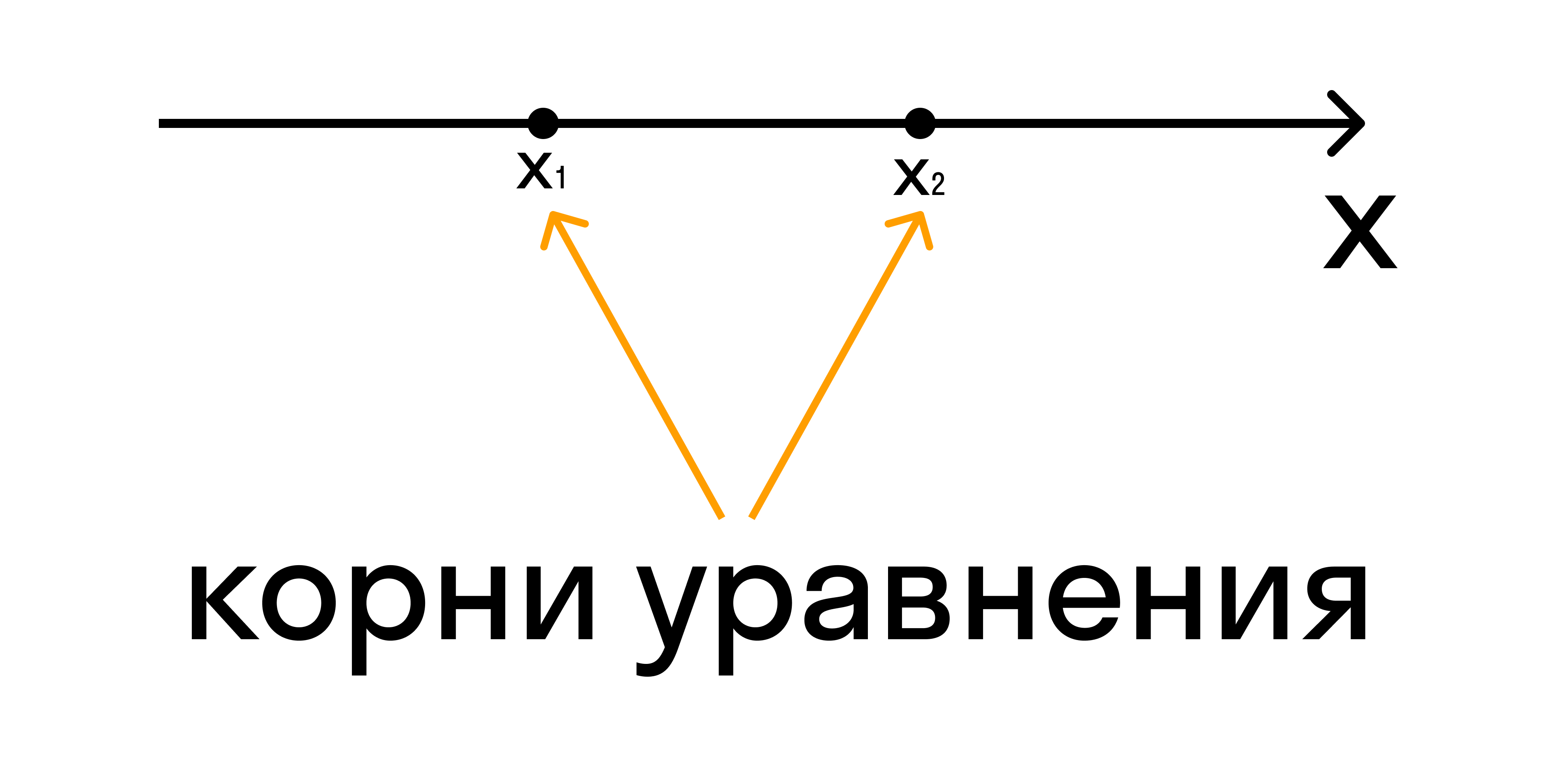
При решении квадратного неравенства необходимо найти корни соответствующего квадратного уравнения ax 2 + bx + c = 0. Чтобы найти корни, нужно найти дискриминант данного уравнения.
Как дискриминант влияет на корни уравнения:
- D = 0. Если дискриминант равен нулю, тогда у квадратного уравнения есть один корень;
- D > 0. Если дискриминант больше нуля, тогда у квадратного уравнения есть два различных корня;
- D 2 + bx + c.
Если требуется найти числовой промежуток, на котором квадратный трехчлен ax 2 + bx + c больше нуля, то этот числовой промежуток находится там, где парабола лежит выше оси ОХ.
Если нужно найти числовой промежуток, на котором квадратный трехчлен ax 2 + bx + c меньше нуля — это числовой промежуток, где парабола лежит ниже оси ОХ.
Если квадратное неравенство нестрогое, то корни входят в числовой промежуток. А если строгое — не входят.
Обучение на курсах по математике в онлайн-школе Skysmart сделает сложные темы понятными, а высокий балл на экзаменах — достижимым!
Видео:Неполные квадратные уравнения. Алгебра, 8 классСкачать

Решение неравенства методом интервалов
Метод интервалов — это специальный алгоритм, который предназначен для решения рациональных неравенств.
Рациональное неравенство имеет вид f(x) ≤ 0, где f(x) — рациональная функция. При этом знак может быть любым: >, 2 + bx + c из левой части квадратного неравенства.
Изобразить координатную прямую и при наличии корней отметить их на ней.
Если неравенство строгое, нужно отметить корни пустыми (выколотыми) точками. Если нестрогое — обычными точками. Именно эти точки разбивают координатную ось на промежутки.
Если неравенство со знаком 2 + 4x — 5, его корнями являются числа -5 и 1, они разбивают числовую ось на три промежутка: (-∞, -5), (-5, 1) и (1, +∞).
Определим знак трехчлена x 2 + 4x — 5 на промежутке (1, +∞). Для этого вычислим значение данного трехчлена при некотором значении x из этого промежутка. Можно брать любое значение переменной, главное — чтобы вычисления были простыми. В нашем случае, возьмем x = 2. Подставим его в трехчлен вместо переменной x:
- 2 2 + 4 * 2 — 5 = 4 + 8 — 5 = 7.
7 — положительное число. Это значит, что любое значение квадратного трехчлена на интервале (1, +∞) будет положительным. Так мы определили знак плюс.
Определим знаки на оставшихся двух промежутках. Начнем с интервала (-5, 1). Из этого интервала можем взять x = 0 и вычислить значение квадратного трехчлена при этом значении переменной:
- 0 2 + 4 * 0 — 5 = 0 + 0 — 5 = -5.
Так как -5 — отрицательное число, то на этом интервале все значения трехчлена будут отрицательными. Так мы определили знак минус.
Осталось определиться со знаком на промежутке (-∞, -5). Возьмем x = -6, подставляем:
- (-6) 2 + 4 * (-6) — 5 = 36 — 24 — 5 = 7.
Следовательно, искомый знак — плюс.
Можно расставить знаки быстрее, если запомнить эти факты:
Видео:Отрицательный дискриминантСкачать

Плюс или минус: как определить знаки
Можно сделать вывод о знаках по значению старшего коэффициента a:
если a > 0, последовательность знаков: +, −, +,
если a 0, последовательность знаков: +, +,
если a 2 — 7 не имеет корней и на промежутке (−∞, +∞) его значения отрицательны, так как коэффициент при x 2 есть отрицательное число -4, и свободный член -7 тоже отрицателен.
- Когда квадратный трехчлен при D > 0 имеет два корня, то знаки его значений на промежутках чередуются. Это значит, что достаточно определить знак на одном из трех промежутков и расставить знаки над оставшимися промежутками, чередуя их. В результате возможна одна из двух последовательностей: +, −, + или −, +, −.
- Если квадратный трехчлен при D = 0 имеет один корень, то этот корень разбивает числовую ось на два промежутка, а знаки над ними будут одинаковыми. Это значит, что достаточно определить знак над одним из них и над другим поставить такой же. При этом получится, либо +, +, либо −, −.
- Когда квадратный трехчлен корней не имеет (D
Теперь мы знаем пошаговый алгоритм. Чтобы закрепить материал потренируемся на примерах и научимся использовать метод интервалов для квадратных неравенств.
Пример 1. Решить неравенство методом интервалов: x^2 — 5x + 6 ≥ 0.
Разложим квадратный трехчлен на множители.
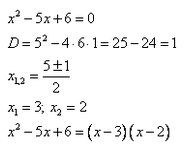
Неравенство примет вид:
Проанализируем два сомножителя:
Первый: х — 3. Этот сомножитель может поменять знак при х = 3, значит при х 0 принимает положительные значения: х — 3 > 0.
Второй: х — 2. Для этого сомножителя такая «знаковая» точка: х = 2.
Вывод: знак произведения (х — 3) * (х — 2) меняется только при переходе переменной через значения х = 3 и х = 2.
В этом весь смысл метода интервалов: определить интервалы значений переменной, на которых ситуация не меняется и рассматривать их как единое целое.
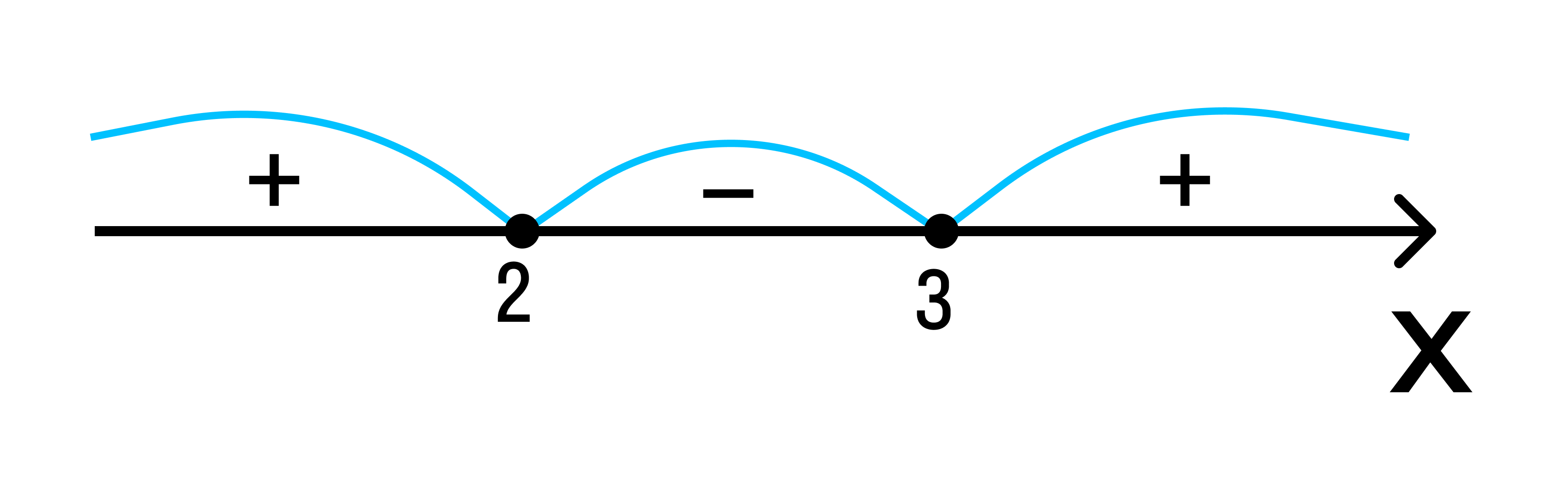
Отобразим эти данные на чертеже:
2 3 — на этом интервале ситуация не изменяется. Значит нужно взять любое значение из этого интервала и подставить его в произведение. Например: х = 25.
- (25 — 3) (25 — 2) = 22*23 = 506 > 0
Вывод: при х > 3 верно неравенство (х — 3) * (х — 2) > 0. Внесем эти данные в чертеж.
Исходное неравенство: (х — 3) * (х — 2) ≥ 0.
Если (х — 3) * (х — 2) > 0:
Если (х — 3) (х — 2) = 0 — при х1 = 3, х2 = 2.
Удовлетворяющие неравенству точки закрасим, а не удовлетворяющие — оставим пустыми.
Ответ: х ≤ 0, х ≥ 3.
Пример 2. Применить метод интервалов для решения неравенства х2+4х+3
Видео:Как решать неравенства? Часть 1| МатематикаСкачать

Алгебра. Урок 8. Неравенства, системы неравенств.
Смотрите бесплатные видео-уроки по теме “Неравенства” на канале Ёжику Понятно.
Видео-уроки на канале Ёжику Понятно. Подпишись!
Содержание страницы:
- Неравенства
- Линейные неравенства
Видео:ИРРАЦИОНАЛЬНЫЕ НЕРАВЕНСТВА неравенства с корнемСкачать

Неравенства
Что такое неравенство? Если взять любое уравнение и знак = поменять на любой из знаков неравенства:
≥ больше или равно,
≤ меньше или равно,
то получится неравенство.
Линейные неравенства
Линейные неравенства – это неравенства вида:
a x b a x ≤ b a x > b a x ≥ b
где a и b – любые числа, причем a ≠ 0, x – переменная.
Примеры линейных неравенств:
3 x 5 x − 2 ≥ 0 7 − 5 x 1 x ≤ 0
Решить линейное неравенство – получить выражение вида:
x c x ≤ c x > c x ≥ c
где c – некоторое число.
Последний шаг в решении неравенства – запись ответа. Давайте разбираться, как правильно записывать ответ.
- Если знак неравенства строгий > , , точка на оси будет выколотой (не закрашенной), а скобка, обнимающая точку – круглой .
Смысл выколотой точки в том, что сама точка в ответ не входит.
- Если знак неравенства нестрогий ≥ , ≤ , точка на оси будет жирной (закрашенной), а скобка, обнимающая точку – квадратной .
Смысл жирной точки в том, что сама точка входит в ответ.
- Скобка, которая обнимает знак бесконечности всегда круглая – не можем мы объять необъятное, как бы нам этого ни хотелось.
Таблица числовых промежутков
| Неравенство | Графическое решение | Форма записи ответа |
|---|---|---|
| x c | x ∈ ( − ∞ ; c ) | |
| x ≤ c | x ∈ ( − ∞ ; c ] | |
| x > c | x ∈ ( c ; + ∞ ) | |
| x ≥ c | Алгоритм решения линейного неравенства
a x b a x ≤ b a x > b a x ≥ b
Примеры решения линейных неравенств: №1. Решить неравенство 3 ( 2 − x ) > 18. Решение: Раскрываем скобки, переносим иксы влево, числа вправо, приводим подобные слагаемые. − 3 x > 18 − 6 − 3 x > 12 | ÷ ( − 3 ) Делим обе части неравенства на ( -3 ) – коэффициент, который стоит перед x . Так как − 3 0 , знак неравенства поменяется на противоположный . x 12 − 3 ⇒ x − 4 Остается записать ответ (см. таблицу числовых промежутков). Ответ: x ∈ ( − ∞ ; − 4 ) №2. Решить неравество 6 x + 4 ≥ 3 ( x + 1 ) − 14. Решение: Раскрываем скобки, переносим иксы влево, числа вправо, приводим подобные слагаемые. 6 x + 4 ≥ 3 x + 3 − 14 6 x − 3 x ≥ 3 − 14 − 4 3 x ≥ − 15 | ÷ 3 Делим обе части неравенства на ( 3 ) – коэффициент, который стоит перед x . Так как 3 > 0, знак неравенства после деления меняться не будет. x ≥ − 15 3 ⇒ x ≥ − 5 Остается записать ответ (см. таблицу числовых промежутков). Особые случаи (в 14 задании ОГЭ 2019 они не встречались, но знать их полезно). №1. Решить неравенство 6 x − 1 ≤ 2 ( 3 x − 0,5 ). Решение: Раскрываем скобки, переносим иксы влево, числа вправо, приводим подобные слагаемые. 6 x − 6 x ≤ − 1 + 1 Получили верное неравенство, которое не зависит от переменной x . Возникает вопрос, какие значения может принимать переменная x , чтобы неравенство выполнялось? Любые! Какое бы значение мы ни взяли, оно все равно сократится и результат неравенства будет верным. Рассмотрим три варианта записи ответа. Ответ:
№2. Решить неравенство x + 3 ( 2 − 3 x ) > − 4 ( 2 x − 12 ). Решение: Раскрываем скобки, переносим иксы влево, числа вправо, приводим подобные слагаемые. x + 6 − 9 x > − 8 x + 48 − 8 x + 8 x > 48 − 6 Получили неверное равенство, которое не зависит от переменной x . Какие бы значения мы ни подставляли в исходное неравенство, результат окажется одним и тем же – неверное неравенство. Ни при каких значениях x исходное неравенство не станет верным. Данное неравенство не имеет решений. Запишем ответ. Квадратные неравенства Квадратные неравенства – это неравенства вида: a x 2 + b x + c > 0 a x 2 + b x + c ≥ 0 a x 2 + b x + c 0 a x 2 + b x + c ≤ 0 где a, b, c — некоторые числа, причем a ≠ 0, x — переменная. Существует универсальный метод решения неравенств степени выше первой (квадратных, кубических, биквадратных и т.д.) – метод интервалов. Если его один раз как следует осмыслить, то проблем с решением любых неравенств не возникнет. Для того, чтобы применять метод интервалов для решения квадратных неравенств, надо уметь хорошо решать квадратные уравнения (см. урок 4). Алгоритм решения квадратного неравенства методом интервалов
Если знак неравенства строгий > , , точки будут выколотые. Если знак неравенства нестрогий ≥ , ≤ , точки будут жирные (заштрихованный).
Если получилось положительное число, знак на интервале плюс. На остальных интервалах знаки будут чередоваться. Точки выколотые, если знак неравенства строгий. Точки жирные, если знак неравенства нестрогий. Если получилось отрицательное число, знак на интервале минус. На остальных интервалах знаки будут чередоваться. Точки выколотые, если знак неравенства строгий. Точки жирные, если знак неравенства нестрогий.
Если знак неравенства > или ≥ в ответ выбираем интервалы со знаком +. Если знак неравенства или ≤ в ответ выбираем интервалы со знаком -. Примеры решения квадратных неравенств: №1. Решить неравенство x 2 ≥ x + 12. Решение: Приводим неравенство к виду a x 2 + b x + c ≥ 0, а затем решаем уравнение a x 2 + b x + c = 0. a = 1, b = − 1, c = − 12 D = b 2 − 4 a c = ( − 1 ) 2 − 4 ⋅ 1 ⋅ ( − 12 ) = 1 + 48 = 49 D > 0 ⇒ будет два различных действительных корня x 1,2 = − b ± D 2 a = − ( − 1 ) ± 49 2 ⋅ 1 = 1 ± 7 2 = [ 1 + 7 2 = 8 2 = 4 1 − 7 2 = − 6 2 = − 3 Наносим точки на ось x . Так как знак неравенства нестрогий, точки будут жирными. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 6 . Подставляем эту точку в исходное выражение: x 2 − x − 1 = 6 2 − 6 − 1 = 29 > 0 Это значит, что знак на интервале, в котором лежит точка 6 будет +. Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный. В ответ пойдут два интервала. В математике для объединения нескольких интервалов используется знак объединения: ∪ . Точки -3 и 4 будут в квадратных скобках, так как они жирные. Ответ: x ∈ ( − ∞ ; − 3 ] ∪ [ 4 ; + ∞ ) №2. Решить неравенство − 3 x − 2 ≥ x 2 . Решение: Приводим неравенство к виду a x 2 + b x + c ≥ 0, а затем решаем уравнение a x 2 + b x + c = 0. a = − 1, b = − 3, c = − 2 D = b 2 − 4 a c = ( − 3 ) 2 − 4 ⋅ ( − 1 ) ⋅ ( − 2 ) = 9 − 8 = 1 D > 0 ⇒ будет два различных действительных корня x 1,2 = − b ± D 2 a = − ( − 3 ) ± 1 2 ⋅ ( − 1 ) = 3 ± 1 − 2 = [ 3 + 1 − 2 = 4 − 2 = − 2 3 − 1 − 2 = 2 − 2 = − 1 x 1 = − 2, x 2 = − 1 Наносим точки на ось x . Так как знак неравенства нестрогий, точки будут жирными. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 0 . Подставляем эту точку в исходное выражение: − x 2 − 3 x − 2 = − ( 0 ) 2 − 3 ⋅ 0 − 2 = − 2 0 Это значит, что знак на интервале, в котором лежит точка 0 будет − . Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный. Поскольку знак неравенства ≥ , выбираем в ответ интервал со знаком +. Точки -2 и -1 будут в квадратных скобках, так как они жирные. Ответ: x ∈ [ − 2 ; − 1 ] №3. Решить неравенство 4 x 2 + 3 x . Решение: Приводим неравенство к виду a x 2 + b x + c ≥ 0, а затем решаем уравнение a x 2 + b x + c = 0. a = − 1, b = − 3, c = 4 D = b 2 − 4 a c = ( − 3 ) 2 − 4 ⋅ ( − 1 ) ⋅ 4 = 9 + 16 = 25 D > 0 ⇒ будет два различных действительных корня x 1,2 = − b ± D 2 a = − ( − 3 ) ± 25 2 ⋅ ( − 1 ) = 3 ± 5 − 2 = [ 3 + 5 − 2 = 8 − 2 = − 4 3 − 5 − 2 = − 2 − 2 = 1 Наносим точки на ось x . Так как знак неравенства строгий, точки будут выколотыми. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 2 . Подставляем эту точку в исходное выражение: − x 2 − 3 x + 4 = − ( 2 ) 2 − 3 ⋅ 2 + 4 = − 6 0 Это значит, что знак на интервале, в котором лежит точка 2 , будет -. Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный. Поскольку знак неравенства , выбираем в ответ интервалы со знаком − . Точки -4 и 1 будут в круглых скобках, так как они выколотые. Ответ: x ∈ ( − ∞ ; − 4 ) ∪ ( 1 ; + ∞ ) №4. Решить неравенство x 2 − 5 x 6. Решение: Приводим неравенство к виду a x 2 + b x + c ≥ 0, а затем решаем уравнение a x 2 + b x + c = 0. a = 1, b = − 5, c = − 6 D = b 2 − 4 a c = ( − 5 ) 2 − 4 ⋅ 1 ⋅ ( − 6 ) = 25 + 25 = 49 D > 0 ⇒ будет два различных действительных корня x 1,2 = − b ± D 2 a = − ( − 5 ) ± 49 2 ⋅ 1 = 5 ± 7 2 = [ 5 + 7 2 = 12 2 = 6 5 − 7 2 = − 2 2 = − 1 Наносим точки на ось x . Так как знак неравенства строгий, точки будут выколотыми. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 10. Подставляем эту точку в исходное выражение: x 2 − 5 x − 6 = 10 2 − 5 ⋅ 10 − 6 = 100 − 50 − 6 = 44 > 0 Это значит, что знак на интервале, в котором лежит точка 10 будет +. Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный. Поскольку знак неравенства , выбираем в ответ интервал со знаком -. Точки -1 и 6 будут в круглых скобках, так как они выколотые Ответ: x ∈ ( − 1 ; 6 ) №5. Решить неравенство x 2 4. Решение: Переносим 4 в левую часть, раскладываем выражение на множители по ФСУ и находим корни уравнения. ( x − 2 ) ( x + 2 ) = 0 ⇔ [ x − 2 = 0 x + 2 = 0 [ x = 2 x = − 2 Наносим точки на ось x . Так как знак неравенства строгий, точки будут выколотыми. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 3 . Подставляем эту точку в исходное выражение: x 2 − 4 = 3 2 − 4 = 9 − 4 = 5 > 0 Это значит, что знак на интервале, в котором лежит точка 3 будет +. Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный. Поскольку знак неравенства , выбираем в ответ интервал со знаком − . Точки -2 и 2 будут в круглых скобках, так как они выколотые. Ответ: x ∈ ( − 2 ; 2 ) №6. Решить неравенство x 2 + x ≥ 0. Решение: Выносим общий множитель за скобку, находим корни уравнения x 2 + x = 0. x ( x + 1 ) = 0 ⇔ [ x = 0 x + 1 = 0 [ x = 0 x = − 1 Наносим точки на ось x . Так как знак неравенства нестрогий, точки будут жирными. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 1 . Подставляем эту точку в исходное выражение: x 2 + x = 1 2 + 1 = 2 > 0 Это значит, что знак на интервале, в котором лежит точка 1 будет +. Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный. Поскольку знак неравенства ≥ , выбираем в ответ интервалы со знаком +. В ответ пойдут два интервала. Точки -1 и 0 будут в квадратных скобках, так как они жирные. Ответ: x ∈ ( − ∞ ; − 1 ] ∪ [ 0 ; + ∞ ) Вот мы и познакомились с методом интервалов. Он нам еще пригодится при решении дробно рациональных неравенств, речь о которых пойдёт ниже. Дробно рациональные неравенства Дробно рациональное неравенство – это неравенство, в котором есть дробь, в знаменателе которой стоит переменная, т.е. неравенство одного из следующих видов: f ( x ) g ( x ) 0 f ( x ) g ( x ) ≤ 0 f ( x ) g ( x ) > 0 f ( x ) g ( x ) ≥ 0 Дробно рациональное неравенство не обязательно сразу выглядит так. Иногда, для приведения его к такому виду, приходится потрудиться (перенести слагаемые в левую часть, привести к общему знаменателю). Примеры дробно рациональных неравенств: x − 1 x + 3 0 3 ( x + 8 ) ≤ 5 x 2 − 1 x > 0 x + 20 x ≥ x + 3 Как же решать эти дробно рациональные неравенства? Да всё при помощи того же всемогущего метода интервалов. Алгоритм решения дробно рациональных неравенств:
f ( x ) g ( x ) 0 f ( x ) g ( x ) ≤ 0 f ( x ) g ( x ) > 0 f ( x ) g ( x ) ≥ 0
В этом пункте алгоритма мы будем делать всё то, что нам запрещали делать все 9 лет обучения в школе – приравнивать знаменатель дроби к нулю. Чтобы как-то оправдать свои буйные действия, полученные точки при нанесении на ось x будем всегда рисовать выколотыми, вне зависимости от того, какой знак неравенства.
Вне зависимости от знака неравенства Если знак неравенства строгий , Если знак неравенства нестрогий ,
Примеры решения дробно рациональных неравенств: №1. Решить неравенство x − 1 x + 3 > 0. Решение: Будем решать данное неравенство в соответствии с алгоритмом.
x = 1 — это ноль числителя . Поскольку знак неравенства строгий, ноль числителя при нанесени на ось x будет выколотым. Запомним это.
x = − 3 — это ноль знаменателя . При нанесении на ось x точка будет всегда выколотой (вне зависимости от знака неравенства) .
При нанесении нулей числителя обращаем внимание на знак неравенства. В данном случае знак неравенства строгий, значит нули числителя будут выколотыми. Ну а нули знаменателя выколоты всегда.
Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 2 . Подставляем эту точку в исходное выражение f ( x ) g ( x ) : x − 1 x + 3 = 2 − 1 2 + 3 = 1 5 > 0, Это значит, что знак на интервале, в котором лежит точка 2 будет +. Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.
Поскольку знак неравенства > , выбираем в ответ интервалы со знаком +. В ответ пойдут два интервала. Точки -3 и 1 будут в круглых скобках, так как обе они выколотые. Ответ: x ∈ ( − ∞ ; − 3 ) ∪ ( 1 ; + ∞ ) №2. Решить неравенство 3 ( x + 8 ) ≤ 5. Решение: Будем решать данное неравенство в соответствии с алгоритмом.
3 ( x + 8 ) − 5 x + 8 ≤ 0 3 x + 8 − 5 ( x + 8 ) x + 8 ≤ 0 3 − 5 ( x + 8 ) x + 8 ≤ 0 3 − 5 x − 40 x + 8 ≤ 0 − 5 x − 37 x + 8 ≤ 0
x = − 37 5 = − 37 5 = − 7,4 x = − 7,4 — ноль числителя . Поскольку знак неравенства нестрогий, при нанесении этой точки на ось x точка будет жирной.
x = − 8 — это ноль знаменателя . При нанесении на ось x , точка будет всегда выколотой (вне зависимости от знака неравенства).
При нанесении нулей числителя обращаем внимание на знак неравенства. В данному случае знак неравенства нестрогий, значит нули числителя будут жирными. Ну а нули знаменателя выколоты всегда.
Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 0 . Подставляем эту точку в исходное выражение f ( x ) g ( x ) : − 5 x − 37 x + 8 = − 5 ⋅ 0 − 37 0 + 8 = − 37 8 0 Это значит, что знак на интервале, в котором лежит точка 0 будет -. Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.
Поскольку знак неравенства ≤ , выбираем в ответ интервалы со знаком -. В ответ пойдут два интервала. Точка -8 будет в круглой скобке, так как она выколотая, точка -7,4 будет в квадратных скобках, так как она жирная. Ответ: x ∈ ( − ∞ ; − 8 ) ∪ [ − 7,4 ; + ∞ ) №3. Решить неравенство x 2 − 1 x > 0. Решение: Будем решать данное неравенство в соответствии с алгоритмом.
( x − 1 ) ( x + 1 ) = 0 ⇒ [ x − 1 = 0 x + 1 = 0 [ x = 1 x = − 1 x 1 = 1, x 2 = − 1 — нули числителя . Поскольку знак неравенства строгий, при нанесении этих точек на ось x точки будут выколотыми.
x = 0 — это ноль знаменателя . При нанесении на ось x , точка будет всегда выколотой (вне зависимости от знака неравенства).
При нанесении нулей числителя обращаем внимание на знак неравенства. В данному случае знак неравенства строгий, значит нули числителя будут выколотыми. Ну а нули знаменателя и так выколоты всегда.
Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 2 . Подставляем эту точку в исходное выражение f ( x ) g ( x ) : x 2 − 1 x = 2 2 − 1 2 = 4 − 1 2 = 3 2 > 0, Это значит, что знак на интервале, в котором лежит точка 2, будет +. Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.
Поскольку знак неравенства > , выбираем в ответ интервалы со знаком +. В ответ пойдут два интервала. Все точки будут в круглых скобках, так как они выколотые. Ответ: x ∈ ( − 1 ; 0 ) ∪ ( 1 ; + ∞ ) Системы неравенств Системой неравенств называют два неравенства с одной неизвестной, которые объединены в общую систему фигурной скобкой. Пример системы неравенств: Алгоритм решения системы неравенств
Примеры решений систем неравенств: №1. Решить систему неравенств < 2 x − 3 ≤ 5 7 − 3 x ≤ 1 Решение: Будем решать данную систему неравенств в соответствии с алгоритмом.
2 x ≤ 8 | ÷ 2 , поскольку 2 > 0, знак неравенства после деления сохраняется. Точка 4 на графике жирная, так как знак неравенства нестрогий.
− 3 x ≤ − 6 | ÷ ( − 3 ), поскольку − 3 0, знак неравенства после деления меняется на противоположный. Графическая интерпретация решения: Точка 2 на графике жирная, так как знак неравенства нестрогий.
Пересечение решений наблюдается на отрезке от 2 до 4 . Точки 2 и 4 в ответе буду в квадратных скобках, так как обе они жирные. №2. Решить систему неравенств < 2 x − 1 ≤ 5 1 − 3 x − 2 Решение: Будем решать данную систему неравенств в соответствии с алгоритмом.
2 x ≤ 6 | ÷ 2 , поскольку 2 > 0, знак неравенства после деления сохраняется. Точка 3 на графике жирная, так как знак неравенства нестрогий.
3 x − 3 | ÷ 3 , поскольку 3 > 0, знак неравенства после деления сохраняется. Графическая интерпретация решения: Точка -1 на графике выколотая, так как знак неравенства строгий.
Пересечение решений наблюдается на самом левом участке. Точка -1 будет в ответе в круглых скобках, так как она выколотая. Ответ: x ∈ ( − ∞ ; − 1 ) №3. Решить систему неравенств 5 − x Решение: Будем решать данную систему неравенств в соответствии с алгоритмом.
Графическая интерпретация решения:
2 x > 12 | ÷ 2 , поскольку 2 > 0, знак неравенства после деления сохраняется. Графическая интерпретация решения:
Пересечений решений не наблюдается. Значит у данной системы неравенств нет решений. №4. Решить систему неравенств 0 2 x + 3 ≤ x 2 Решение: Будем решать данную систему неравенств в соответствии с алгоритмом.
Графическая интерпретация решения первого неравенства:
Решаем методом интервалов. a = − 1, b = 2, c = 3 D = b 2 − 4 a c = 2 2 − 4 ⋅ ( − 1 ) ⋅ 3 = 4 + 12 = 16 D > 0 — два различных действительных корня. x 1,2 = − b ± D 2 a = − 2 ± 16 2 ⋅ ( − 1 ) = − 2 ± 4 − 2 = [ − 2 − 4 − 2 = − 6 − 2 = 3 − 2 + 4 − 2 = 2 − 2 = − 1 Наносим точки на ось x и расставляем знаки на интервалах. Поскольку знак неравенства нестрогий, обе точки будут заштрихованными. Графическая интерпретация решения второго неравенства:
Пересечение решений наблюдается в двух интервалах. Для того, чтобы в ответе объединить два интервала, используется знак объединения ∪ . Точка -4 будет в круглой скобке, так как она выколотая, а точки -1 и 3 в квадратных, так как они жирные. Видео:Как решать уравнение с корнями Иррациональное уравнение Как решать уравнение с корнем х под корнемСкачать  Решение неравенств: основные ошибки и полезные лайфхакиВы умеете решать неравенства? Уверены? Вспомним для начала, что вообще можно делать с неравенствами и чего с ними делать нельзя. При решении неравенств мы можем: 1. Умножать обе части неравенства на число или выражение, не равное нулю. При умножении обеих частей неравенства на отрицательное число знак неравенства меняется на противоположный. 2. Можем возводить обе части неравенства в квадрат при условии, что они неотрицательны 3. Имея дело с показательным или логарифмическим неравенством, мы можем «отбрасывать» основания или логарифмы. Если основание степени или логарифма больше единицы – знак неравенства будет тот же. Если основание степени или логарифма положительно и меньше единицы – знак неравенства меняется на противоположный. Конечно, мы не просто «отбрасываем» основания степеней или логарифмы. Мы пользуемся свойствами монотонности соответствующих функций. Если основание степени больше единицы, показательная функция монотонно возрастает. Если основание положительно и меньше единицы – показательная функция монотонно убывает. Аналогично ведет себя и логарифмическая функция. 4. При решении показательных или логарифмических неравенств применяется метод рационализации (замены множителя). 5. Общее правило. Если неравенство можно хоть как-то упростить – это необходимо сделать! Иначе его решение может занять восемь страниц и два часа времени. Чего нельзя делать при решении неравенств? Вот 7 ловушек, в которые часто попадают абитуриенты. 1. Нельзя умножать (или делить) неравенство на выражение, знака которого мы не знаем. Например, в неравенстве > нельзя поделить левую и правую часть на . Правильный способ: перенести всё в левую часть неравенства, разложить на множители и решить неравенство методом интервалов. Получаем, что . «Сократив» на , который может быть отрицательным, мы не получили бы правильного ответа. 2. Извлекать из неравенства корень тоже нельзя. Такого действия просто нет. Как, например, решить неравенство Перенесем все в левую часть неравенства, чтобы в правой остался ноль. Разложим левую часть на множители. Решим неравенство, пользуясь свойствами квадратичной функции , и запишем ответ: . Запомним: ответы типа « > » абсурдны. Как решать неравенство > 0? Это типичная «ловушка для абитуриентов». Так и хочется сказать, что > 0 (то есть извлечь корень из неравенства). Но этого делать нельзя. Выражение положительно при всех , кроме нуля. Правильное решение неравенства: . 4. Возводить обе части неравенства в квадрат можно только если они неотрицательны. 5. Помним о том, в каких случаях знак показательного или логарифмического неравенства меняется, а в каких – остается тем же. «Отбрасывая» логарифмы, делаем это грамотно. 6. Если в неравенстве есть дроби, корни четной степени или логарифмы – там обязательно будет область допустимых значений. 7. Сложная тем для старшеклассников – задачи с модулем. Проверьте, умеете ли вы их решать. При решении неравенств большое значение имеет правильное оформление. Рекомендуется оформлять решение как цепочку равносильных переходов: от исходного неравенства к равносильному ему неравенству или системе. Обратите внимание на приемы, позволяющие решать неравенства легко, быстро и без лишних вычислений. А теперь – полезный лайфхак для решения дробно-рациональных неравенств. Что будет, если действовать «по шаблону» — то есть собрать всё в левой части неравенства и привести к одному знаменателю? — Будет много вычислений и выражение четвертой степени. Может быть, сделаем проще? Представим дробь в виде суммы дробей и . Продолжаем упрощать левую часть: Теперь можно и привести дроби к одному знаменателю. Все, больше ничего не пишем. Решаем неравенство методом интервалов. 🔥 ВидеоКак решать уравнения с модулем или Математический торт с кремом (часть 1) | МатематикаСкачать  Иррациональное неравенство #8Скачать  Квадратные неравенства: что делать, если нет корнейСкачать  Как понять неравенства? Квадратные неравенства. Линейные и сложные неравенства | TutorOnlineСкачать  СУПЕР ЛАЙФХАК — Как решать Иррациональные УравненияСкачать  Подготовка к ОГЭ . Рациональные неравенства | Математика | TutorOnlineСкачать  Решение биквадратных уравнений. 8 класс.Скачать  Решение неравенства методом интерваловСкачать  ЛИНЕЙНЫЕ УРАВНЕНИЯ - Как решать линейные уравнения // Подготовка к ЕГЭ по МатематикеСкачать  5 способов решения квадратного уравнения ➜ Как решать квадратные уравнения?Скачать  Что такое параметр? Уравнения и неравенства с параметром. 7-11 класс. Вебинар | МатематикаСкачать  СЛОЖИТЕ ДВА КОРНЯСкачать  Как решать неравенства? Математика 10 класс | TutorOnlineСкачать  |