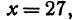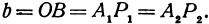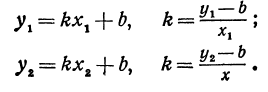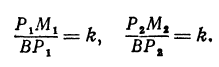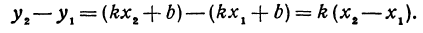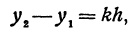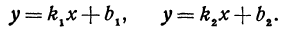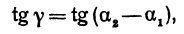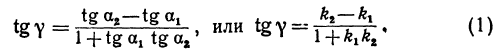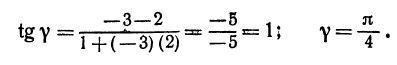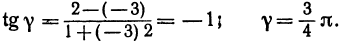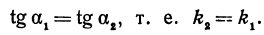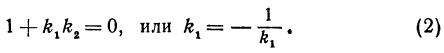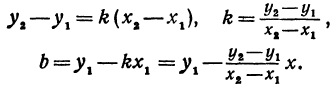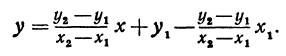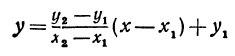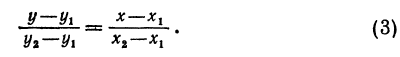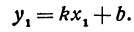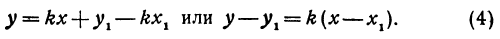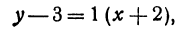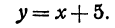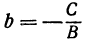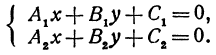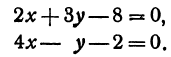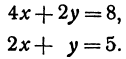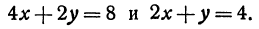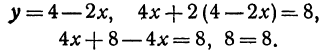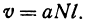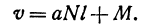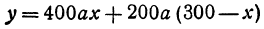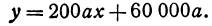Данная статья продолжает тему уравнения прямой на плоскости: рассмотрим такой вид уравнения, как общее уравнение прямой. Зададим теорему и приведем ее доказательство; разберемся, что такое неполное общее уравнение прямой и как осуществлять переходы от общего уравнения к другим типам уравнений прямой. Всю теорию закрепим иллюстрациями и решением практических задач.
- Общее уравнение прямой: основные сведения
- Неполное уравнение общей прямой
- Общее уравнение прямой, проходящей через заданную точку плоскости
- Переход от общего уравнения прямой к прочим видам уравнений прямой и обратно
- Составление общего уравнения прямой
- Глава 1. Уравнение прямой (стр. 1 )
- Глава 1. Уравнение прямой
- 1. 1. Формы записи уравнения прямой
- 1. 2. Положение точек относительно прямой
- 1.3. Взаимное расположение двух отрезков
- 1.4. Точка пересечения отрезков
- 2.1 Расстояния между точками. Расстояние от точки до прямой
- 2.2. Расстояние между точкой и отрезком
- § 3. Многоугольники
- 3.1. Виды многоугольников
- 3.2. Выпуклость многоугольников
- Линейная функция — определение и вычисление с примерами решения
- Основное свойство линейной функции
- Задачи на прямую
- Общее уравнение прямой. Неявная линейная функция
- Система двух уравнений первой степени
- Примеры применения линейной функции
- Практика. Решение задач. Часть 1. Уравнения прямой
- 🌟 Видео
Видео:Уравнение прямой в пространстве через 2 точки. 11 класс.Скачать

Общее уравнение прямой: основные сведения
Пусть на плоскости задана прямоугольная система координат O x y .
Любое уравнение первой степени, имеющее вид A x + B y + C = 0 , где А , В , С – некоторые действительные числа ( А и В не равны одновременно нулю) определяет прямую линию в прямоугольной системе координат на плоскости. В свою очередь, любая прямая в прямоугольной системе координат на плоскости определяется уравнением, имеющим вид A x + B y + C = 0 при некотором наборе значений А , В , С .
указанная теорема состоит из двух пунктов, докажем каждый из них.
- Докажем, что уравнение A x + B y + C = 0 определяет на плоскости прямую.
Пусть существует некоторая точка М 0 ( x 0 , y 0 ) , координаты которой отвечают уравнению A x + B y + C = 0 . Таким образом: A x 0 + B y 0 + C = 0 . Вычтем из левой и правой частей уравнений A x + B y + C = 0 левую и правую части уравнения A x 0 + B y 0 + C = 0 , получим новое уравнение, имеющее вид A ( x — x 0 ) + B ( y — y 0 ) = 0 . Оно эквивалентно A x + B y + C = 0 .
Полученное уравнение A ( x — x 0 ) + B ( y — y 0 ) = 0 является необходимым и достаточным условием перпендикулярности векторов n → = ( A , B ) и M 0 M → = ( x — x 0 , y — y 0 ) . Таким образом, множество точек M ( x , y ) задает в прямоугольной системе координат прямую линию, перпендикулярную направлению вектора n → = ( A , B ) . Можем предположить, что это не так, но тогда бы векторы n → = ( A , B ) и M 0 M → = ( x — x 0 , y — y 0 ) не являлись бы перпендикулярными, и равенство A ( x — x 0 ) + B ( y — y 0 ) = 0 не было бы верным.
Следовательно, уравнение A ( x — x 0 ) + B ( y — y 0 ) = 0 определяет некоторую прямую в прямоугольной системе координат на плоскости, а значит и эквивалентное ему уравнение A x + B y + C = 0 определяет ту же прямую. Так мы доказали первую часть теоремы.
- Приведем доказательство, что любую прямую в прямоугольной системе координат на плоскости можно задать уравнением первой степени A x + B y + C = 0 .
Зададим в прямоугольной системе координат на плоскости прямую a ; точку M 0 ( x 0 , y 0 ) , через которую проходит эта прямая, а также нормальный вектор этой прямой n → = ( A , B ) .
Пусть также существует некоторая точка M ( x , y ) – плавающая точка прямой. В таком случае, векторы n → = ( A , B ) и M 0 M → = ( x — x 0 , y — y 0 ) являются перпендикулярными друг другу, и их скалярное произведение есть нуль:
n → , M 0 M → = A ( x — x 0 ) + B ( y — y 0 ) = 0
Перепишем уравнение A x + B y — A x 0 — B y 0 = 0 , определим C : C = — A x 0 — B y 0 и в конечном результате получим уравнение A x + B y + C = 0 .
Так, мы доказали и вторую часть теоремы, и доказали всю теорему в целом.
Уравнение, имеющее вид A x + B y + C = 0 – это общее уравнение прямой на плоскости в прямоугольной системе координат O x y .
Опираясь на доказанную теорему, мы можем сделать вывод, что заданные на плоскости в фиксированной прямоугольной системе координат прямая линия и ее общее уравнение неразрывно связаны. Иначе говоря, исходной прямой соответствует ее общее уравнение; общему уравнению прямой соответствует заданная прямая.
Из доказательства теоремы также следует, что коэффициенты А и В при переменных x и y являются координатами нормального вектора прямой, которая задана общим уравнением прямой A x + B y + C = 0 .
Рассмотрим конкретный пример общего уравнения прямой.
Пусть задано уравнение 2 x + 3 y — 2 = 0 , которому соответствует прямая линия в заданной прямоугольной системе координат. Нормальный вектор этой прямой – это вектор n → = ( 2 , 3 ) . Изобразим заданную прямую линию на чертеже.
Также можно утверждать и следующее: прямая, которую мы видим на чертеже, определяется общим уравнением 2 x + 3 y — 2 = 0 , поскольку координаты всех точек заданной прямой отвечают этому уравнению.
Мы можем получить уравнение λ · A x + λ · B y + λ · C = 0 , умножив обе части общего уравнения прямой на число λ , не равное нулю. Полученное уравнение является эквивалентом исходного общего уравнения, следовательно, будет описывать ту же прямую на плоскости.
Видео:9 класс, 7 урок, Уравнение прямойСкачать

Неполное уравнение общей прямой
Полное общее уравнение прямой – такое общее уравнение прямой A x + B y + C = 0 , в котором числа А , В , С отличны от нуля. В ином случае уравнение является неполным.
Разберем все вариации неполного общего уравнения прямой.
- Когда А = 0 , В ≠ 0 , С ≠ 0 , общее уравнение принимает вид B y + C = 0 . Такое неполное общее уравнение задает в прямоугольной системе координат O x y прямую, которая параллельна оси O x , поскольку при любом действительном значении x переменная y примет значение — C B . Иначе говоря, общее уравнение прямой A x + B y + C = 0 , когда А = 0 , В ≠ 0 , задает геометрическое место точек ( x , y ) , координаты которых равны одному и тому же числу — C B .
- Если А = 0 , В ≠ 0 , С = 0 , общее уравнение принимает вид y = 0 . Такое неполное уравнение определяет ось абсцисс O x .
- Когда А ≠ 0 , В = 0 , С ≠ 0 , получаем неполное общее уравнение A x + С = 0 , задающее прямую, параллельную оси ординат.
- Пусть А ≠ 0 , В = 0 , С = 0 , тогда неполное общее уравнение примет вид x = 0 , и это есть уравнение координатной прямой O y .
- Наконец, при А ≠ 0 , В ≠ 0 , С = 0 , неполное общее уравнение принимает вид A x + B y = 0 . И это уравнение описывает прямую, которая проходит через начало координат. В самом деле, пара чисел ( 0 , 0 ) отвечает равенству A x + B y = 0 , поскольку А · 0 + В · 0 = 0 .
Графически проиллюстрируем все вышеуказанные виды неполного общего уравнения прямой.
Известно, что заданная прямая параллельна оси ординат и проходит через точку 2 7 , — 11 . Необходимо записать общее уравнение заданной прямой.
Решение
Прямая, параллельная оси ординат, задается уравнением вида A x + C = 0 , в котором А ≠ 0 . Также условием заданы координаты точки, через которую проходит прямая, и координаты этой точки отвечают условиям неполного общего уравнения A x + C = 0 , т.е. верно равенство:
Из него возможно определить C , если придать A какое-то ненулевое значение, к примеру, A = 7 . В таком случае получим: 7 · 2 7 + C = 0 ⇔ C = — 2 . Нам известны оба коэффициента A и C , подставим их в уравнение A x + C = 0 и получим требуемое уравнение прямой: 7 x — 2 = 0
Ответ: 7 x — 2 = 0
На чертеже изображена прямая, необходимо записать ее уравнение.
Решение
Приведенный чертеж позволяет нам легко взять исходные данные для решения задачи. Мы видим на чертеже, что заданная прямая параллельна оси O x и проходит через точку ( 0 , 3 ) .
Прямую, которая параллельна очи абсцисс, определяет неполное общее уравнение B y + С = 0 . Найдем значения B и C . Координаты точки ( 0 , 3 ) , поскольку через нее проходит заданная прямая, будут удовлетворять уравнению прямой B y + С = 0 , тогда справедливым является равенство: В · 3 + С = 0 . Зададим для В какое-то значение, отличное от нуля. Допустим, В = 1 , в таком случае из равенства В · 3 + С = 0 можем найти С : С = — 3 . Используем известные значения В и С , получаем требуемое уравнение прямой: y — 3 = 0 .
Ответ: y — 3 = 0 .
Видео:Как составить уравнение прямой, проходящей через две точки на плоскости | МатематикаСкачать

Общее уравнение прямой, проходящей через заданную точку плоскости
Пусть заданная прямая проходит через точку М 0 ( x 0 , y 0 ) , тогда ее координаты отвечают общему уравнению прямой, т.е. верно равенство: A x 0 + B y 0 + C = 0 . Отнимем левую и правую части этого уравнения от левой и правой части общего полного уравнения прямой. Получим: A ( x — x 0 ) + B ( y — y 0 ) + C = 0 , это уравнение эквивалентно исходному общему, проходит через точку М 0 ( x 0 , y 0 ) и имеет нормальный вектор n → = ( A , B ) .
Результат, который мы получили, дает возможность записывать общее уравнение прямой при известных координатах нормального вектора прямой и координатах некой точки этой прямой.
Даны точка М 0 ( — 3 , 4 ) , через которую проходит прямая, и нормальный вектор этой прямой n → = ( 1 , — 2 ) . Необходимо записать уравнение заданной прямой.
Решение
Исходные условия позволяют нам получить необходимые данные для составления уравнения: А = 1 , В = — 2 , x 0 = — 3 , y 0 = 4 . Тогда:
A ( x — x 0 ) + B ( y — y 0 ) = 0 ⇔ 1 · ( x — ( — 3 ) ) — 2 · y ( y — 4 ) = 0 ⇔ ⇔ x — 2 y + 22 = 0
Задачу можно было решить иначе. Общее уравнение прямой имеет вид A x + B y + C = 0 . Заданный нормальный вектор позволяет получить значения коэффициентов A и B , тогда:
A x + B y + C = 0 ⇔ 1 · x — 2 · y + C = 0 ⇔ x — 2 · y + C = 0
Теперь найдем значение С, используя заданную условием задачи точку М 0 ( — 3 , 4 ) , через которую проходит прямая. Координаты этой точки отвечают уравнению x — 2 · y + C = 0 , т.е. — 3 — 2 · 4 + С = 0 . Отсюда С = 11 . Требуемое уравнение прямой принимает вид: x — 2 · y + 11 = 0 .
Ответ: x — 2 · y + 11 = 0 .
Задана прямая 2 3 x — y — 1 2 = 0 и точка М 0 , лежащая на этой прямой. Известна лишь абсцисса этой точки, и она равна — 3 . Необходимо определить ординату заданной точки.
Решение
Зададим обозначение координат точки М 0 как x 0 и y 0 . В исходных данных указано, что x 0 = — 3 . Поскольку точка принадлежит заданной прямой, значит ее координаты отвечают общему уравнению этой прямой. Тогда верным будет равенство:
2 3 x 0 — y 0 — 1 2 = 0
Определяем y 0 : 2 3 · ( — 3 ) — y 0 — 1 2 = 0 ⇔ — 5 2 — y 0 = 0 ⇔ y 0 = — 5 2
Ответ: — 5 2
Видео:Видеоурок "Общие уравнения прямой"Скачать

Переход от общего уравнения прямой к прочим видам уравнений прямой и обратно
Как мы знаем, существует несколько видов уравнения одной и той же прямой на плоскости. Выбор вида уравнения зависит от условий задачи; возможно выбирать тот, который более удобен для ее решения. Здесь очень пригодится навык преобразования уравнения одного вида в уравнение другого вида.
Для начала рассмотрим переход от общего уравнения вида A x + B y + C = 0 к каноническому уравнению x — x 1 a x = y — y 1 a y .
Если А ≠ 0 , тогда переносим слагаемое B y в правую часть общего уравнения. В левой части выносим A за скобки. В итоге получаем: A x + C A = — B y .
Это равенство возможно записать как пропорцию: x + C A — B = y A .
В случае, если В ≠ 0 , оставляем в левой части общегь уравнения только слагаемое A x , прочие переносим в правую часть, получаем: A x = — B y — C . Выносим – В за скобки, тогда: A x = — B y + C B .
Перепишем равенство в виде пропорции: x — B = y + C B A .
Конечно, заучивать полученные формулы нет необходимости. Достаточно знать алгоритм действий при переходе от общего уравнения к каноническому.
Задано общее уравнение прямой 3 y — 4 = 0 . Необходимо преобразовать его в каноническое уравнение.
Решение
Запишем исходное уравнение как 3 y — 4 = 0 . Далее действуем по алгоритму: в левой части остаётся слагаемое 0 x ; а в правой части выносим — 3 за скобки; получаем: 0 x = — 3 y — 4 3 .
Запишем полученное равенство как пропорцию: x — 3 = y — 4 3 0 . Так, мы получили уравнение канонического вида.
Ответ: x — 3 = y — 4 3 0 .
Чтобы преобразовать общее уравнение прямой в параметрические, сначала осуществляют переход к каноническому виду, а затем переход от канонического уравнения прямой к параметрическим уравнениям.
Прямая задана уравнением 2 x — 5 y — 1 = 0 . Запишите параметрические уравнения этой прямой.
Решение
Осуществим переход от общего уравнения к каноническому:
2 x — 5 y — 1 = 0 ⇔ 2 x = 5 y + 1 ⇔ 2 x = 5 y + 1 5 ⇔ x 5 = y + 1 5 2
Теперь примем обе части полученного канонического уравнения равными λ , тогда:
x 5 = λ y + 1 5 2 = λ ⇔ x = 5 · λ y = — 1 5 + 2 · λ , λ ∈ R
Ответ: x = 5 · λ y = — 1 5 + 2 · λ , λ ∈ R
Общее уравнение можно преобразовать в уравнение прямой с угловым коэффициентом y = k · x + b , но только тогда, когда В ≠ 0 . Для перехода в левой части оставляем слагаемое B y , остальные переносятся в правую. Получим: B y = — A x — C . Разделим обе части полученного равенство на B , отличное от нуля: y = — A B x — C B .
Задано общее уравнение прямой: 2 x + 7 y = 0 . Необходимо преобразовать то уравнение в уравнение с угловым коэффициентом.
Решение
Произведем нужные действия по алгоритму:
2 x + 7 y = 0 ⇔ 7 y — 2 x ⇔ y = — 2 7 x
Ответ: y = — 2 7 x .
Из общего уравнения прямой достаточно просто получить уравнение в отрезках вида x a + y b = 1 . Чтобы осуществить такой переход, перенесем число C в правую часть равенства, разделим обе части полученного равенства на – С и, наконец, перенесем в знаменатели коэффициенты при переменных x и y :
A x + B y + C = 0 ⇔ A x + B y = — C ⇔ ⇔ A — C x + B — C y = 1 ⇔ x — C A + y — C B = 1
Необходимо преобразовать общее уравнение прямой x — 7 y + 1 2 = 0 в уравнение прямой в отрезках.
Решение
Перенесем 1 2 в правую часть: x — 7 y + 1 2 = 0 ⇔ x — 7 y = — 1 2 .
Разделим на -1/2 обе части равенства: x — 7 y = — 1 2 ⇔ 1 — 1 2 x — 7 — 1 2 y = 1 .
Преобразуем далее в необходимый вид: 1 — 1 2 x — 7 — 1 2 y = 1 ⇔ x — 1 2 + y 1 14 = 1 .
Ответ: x — 1 2 + y 1 14 = 1 .
В общем, несложно производится и обратный переход: от прочих видов уравнения к общему.
Уравнение прямой в отрезках и уравнение с угловым коэффициентом легко преобразовать в общее, просто собрав все слагаемые в левой части равенства:
x a + y b ⇔ 1 a x + 1 b y — 1 = 0 ⇔ A x + B y + C = 0 y = k x + b ⇔ y — k x — b = 0 ⇔ A x + B y + C = 0
Каноническое уравнение преобразуется к общему по следующей схеме:
x — x 1 a x = y — y 1 a y ⇔ a y · ( x — x 1 ) = a x ( y — y 1 ) ⇔ ⇔ a y x — a x y — a y x 1 + a x y 1 = 0 ⇔ A x + B y + C = 0
Для перехода от параметрических сначала осуществляется переход к каноническому, а затем – к общему:
x = x 1 + a x · λ y = y 1 + a y · λ ⇔ x — x 1 a x = y — y 1 a y ⇔ A x + B y + C = 0
Заданы параметрические уравнения прямой x = — 1 + 2 · λ y = 4 . Необходимо записать общее уравнение этой прямой.
Решение
Осуществим переход от параметрических уравнений к каноническому:
x = — 1 + 2 · λ y = 4 ⇔ x = — 1 + 2 · λ y = 4 + 0 · λ ⇔ λ = x + 1 2 λ = y — 4 0 ⇔ x + 1 2 = y — 4 0
Перейдем от канонического к общему:
x + 1 2 = y — 4 0 ⇔ 0 · ( x + 1 ) = 2 ( y — 4 ) ⇔ y — 4 = 0
Ответ: y — 4 = 0
Задано уравнение прямой в отрезках x 3 + y 1 2 = 1 . Необходимо осуществить переход к общему виду уравнения.
Решение:
Просто перепишем уравнение в необходимом виде:
x 3 + y 1 2 = 1 ⇔ 1 3 x + 2 y — 1 = 0
Ответ: 1 3 x + 2 y — 1 = 0 .
Видео:Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

Составление общего уравнения прямой
Выше мы говорили о том, что общее уравнение возможно записать при известных координатах нормального вектора и координатах точки, через которую проходит прямая. Такая прямая определяется уравнением A ( x — x 0 ) + B ( y — y 0 ) = 0 . Там же мы разобрали соответствующий пример.
Сейчас рассмотрим более сложные примеры, в которых для начала необходимо определить координаты нормального вектора.
Задана прямая, параллельная прямой 2 x — 3 y + 3 3 = 0 . Также известна точка M 0 ( 4 , 1 ) , через которую проходит заданная прямая. Необходимо записать уравнение заданной прямой.
Решение
Исходные условия говорят нам о том, что прямые параллельны, тогда, как нормальный вектор прямой, уравнение которой требуется записать, возьмем направляющий вектор прямой n → = ( 2 , — 3 ) : 2 x — 3 y + 3 3 = 0 . Теперь нам известны все необходимые данные, чтобы составить общее уравнение прямой:
A ( x — x 0 ) + B ( y — y 0 ) = 0 ⇔ 2 ( x — 4 ) — 3 ( y — 1 ) = 0 ⇔ 2 x — 3 y — 5 = 0
Ответ: 2 x — 3 y — 5 = 0 .
Заданная прямая проходит через начало координат перпендикулярно прямой x — 2 3 = y + 4 5 . Необходимо составить общее уравнение заданной прямой.
Решение
Нормальный вектором заданной прямой будет направляющий вектор прямой x — 2 3 = y + 4 5 .
Тогда n → = ( 3 , 5 ) . Прямая проходит через начало координат, т.е. через точку О ( 0 , 0 ) . Составим общее уравнение заданной прямой:
A ( x — x 0 ) + B ( y — y 0 ) = 0 ⇔ 3 ( x — 0 ) + 5 ( y — 0 ) = 0 ⇔ 3 x + 5 y = 0
Видео:Уравнение прямой.Скачать

Глава 1. Уравнение прямой (стр. 1 )
 | Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 |
Видео:Геометрия 9 класс (Урок№9 - Уравнение линии на плоскости. Уравнение окружности. Уравнение прямой.)Скачать

Глава 1. Уравнение прямой
Геометрия развивается по многим направлениям. Возникновение компьютеров привело к появлению такой области математики как вычислительная геометрия. При создании современных приложений часто требуется разработка эффективных алгоритмов для определения взаиморасположения различных объектов на плоскости, вычисления расстояний между ними, вычисления площадей фигур и др.
В данной главе излагается материал, частично известный вам из курса математики. Мы рассмотрим методы решения геометрических задач, которые эффективно реализуются с помощью компьютера, что позволит вам по другому взглянуть на вопросы, изучаемые в рамках школьного курса геометрии. Для этого придется воспользоваться аналитическим представлением геометрических объектов.
1. 1. Формы записи уравнения прямой
В задачах часто приходится задавать на плоскости различные геометрические объекты. Простейшими геометрическими фигурами на плоскости являются точка и прямая. Точка задается указанием своих координат, например A(15; –5), B(x1; y1). Прямую можно задавать с помощью уравнения прямой. Существуют различные формы записи уравнения прямой. Выбор какой-то конкретной зависит от исходных данных, задающих прямую на плоскости. (Могут быть заданы координаты двух точек, через которые проводится прямая, или коэффициенты при неизвестных в линейном уравнении).
В декартовых координатах каждая прямая определяется уравнением первой степени. Уравнение вида
называется общим уравнением прямой.
Если в общем уравнении прямой коэффициент при y не равен нулю, то уравнение можно разрешить относительно y:
Обозначая k = 

получаем уравнение вида y = kx + b. Если же B = 0, то уравнение имеет вид
Уравнение y = kx + b называется уравнением прямой с угловым коэффициентом; k – угловой коэффициент, b – величина отрезка, который отсекает прямая на оси Oy, считая от начала координат (рис. 1).
Уравнение y – y0 = k(x–x0) – это уравнение прямой с угловым коэффициентом k, которая проходит через точку с координатами (x0; y0).
Рассмотрим две точки с координатами (x1; y1) и (x2; y2), лежащие на прямой y = kx + b. Их координаты удовлетворяют уравнению прямой:
Вычитая из второго равенства первое, имеем y2 – y1 = k(x2 – x1), или
k =
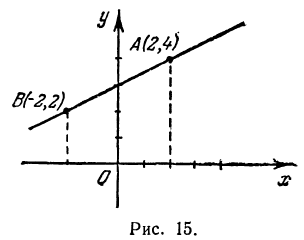
Пусть точка с координатами (x; y) – произвольная точка на прямой, проходящей через точки с координатами (x1; y1) и (x2; y2) ( рис. 2 ). Тогда, с учетом того факта, что она имеет тот же коэффициент наклона, получаем
k =




является уравнением прямой, которая проходит через точки с координатами (x1; y1) и (x2; y2). Недостатком этой формулы является ее неопределенность при x1 = x2 и (или) y1 = y2. Поэтому ее лучше использовать в виде
Алгоритм для определения значений коэффициентов A, B, C общего уравнения прямой, проходящей через точки (x1; y1) и (x2; y2), будет следующим [1] :
C:= – x1*(y2 – y1)+y1*(x2 – x1)
Рассмотрим пример: x1 = 0, y1 = 0, x2 = 1, y2 = 2. Уравнение прямой, проходящей через точки (x1; y1) и (x2; y2) будет следующим:
C = –x1 * (y2 – y1) + y1 * (x2 – x1) = 0 * 2 + 0 * 1 = 0. ЌСледовательно, уравнение прямой будет иметь вид 2х – у = 0.
1. 2. Положение точек относительно прямой
Множество точек прямой, проходящей через две точки с координатами (x1; y1) и (x2; y2), удовлетворяет уравнению
Это значит, что если имеется точка с координатами (x0; y0) и (x0 – x1) * (y2 – y1) – (y0 – y1) * (x2 – x1) = 0, то эта точка лежит на прямой. B дальнейшем, вместо выражения (x – x1) * (y2 – y1) – (y – y1) * (x2 – x1) мы иногда будем использовать для краткости обозначение Ax + By + C или f(x1, y1, x2, y2, x, y).
Прямая Ax + By + C = 0, проходящая через две заданные точки с координатами (x1; y1) и (x2; y2), разбивает плоскость на две полуплоскости. Рассмотрим возможные значения выражения Ax + By + C.
1) Ax + By + C = 0 – определяет геометрическое место точек, лежащих на прямой.
Запишем алгоритм для определения, лежит ли точка с координатами (x3; y3) на прямой, проходящей через точки (x1; y1) и (x2; y2). Переменная P – переменная логического типа, которая имеет значение «истина», если точка лежит на прямой и «ложь» в противном случае.
если (x3 – x1)*(y2 – y1) – (y3 – y1)*(x2 – x1)=0
2) Ax + By + C > 0 – определяет геометрическое место точек, лежащих по одну сторону от прямой.
3) Ax + By + C рис. 3 точки (x3; y3) и (x4; y4) лежат по одну сторону от прямой, точки (x3; y3) и (x5; y5) по разные стороны от прямой, а точка (x6; y6) лежит на прямой.
Рассмотрим пример: x1 = 1, y1 = 2, x2 = 5, y2 = 6. Уравнение прямой, проходящей через точки (x1; y1) и (x2; y2), будет следующим:
Следовательно, уравнение прямой будет иметь вид 4х – 4у + 4 = 0 или x – y + 1 = 0. Подставим координаты точек (3; 4), (1; 1), (2; 0), (0; 2) в уравнение прямой. Получим:
1 * 3 – 1 * 4 + 1 = 0, 1 * 2 – 1 * 0 + 1 > 0,
1 * 1 – 1 * 1 + 1 > 0, 1 * 0 – 1 * 2 + 1 L:=»по одну»
Z1:=(x3 – x1)*(y2 – y1) – (y3 – y1)*(x2 – x1)
Z2:=(x4 – x1)*(y2 – y1) – (y4 – y1)*(x2 – x1)
½ то L:=»по разные» (1. 3)
1.3. Взаимное расположение двух отрезков
Пусть нам необходимо определить взаимное расположение двух отрезков. Отрезки на плоскости заданы координатами своих концевых точек. Предположим, что концевые точки одного из отрезков имеют координаты (x1; y1) и (x2; y2), а концевые точки другого – (x3; y3) и (x4; y4). Пусть общее уравнение первой прямой, проходящей через точки (x1;y1) и (x2;y2), имеет вид A1x + B1y + C1 = 0, а второй прямой, проходящей через точки (x3;y3) и (x4;y4), A2x + B2y + C2 = 0.
Определим расположение точек (x3; y3) и (x4; y4) относительно первой прямой. Если они расположены по одну сторону от прямой, то отрезки не могут пересекаться. Аналогично можно определить положение точек (x1; y1) и (x2; y2) относительно другой прямой.
Таким образом, если значения пары выражений Z1 = A1x3 + B1y3 + C1 и Z2 = A1x4 + B1y4 + C1 имеют разные знаки или Z1*Z2 = 0, а также пары Z3 = A2x1 + B2y1 + C2 и Z4 = A2x2 + B2y2 + C2 имеют разные знаки или Z3*Z4 = 0, то отрезки пересекаются. Если же значения пар выражений Z1 и Z2, или Z3 и Z4, имеют одинаковые знаки, то отрезки не пересекаются.
Различные случаи расположения отрезков показаны на рис. 4 .
На этом рисунке отрезки с концами в точках (x1; y1), (x2; y2) и (x4; y4), (x5; y5) пересекаются, отрезки с концами в точках (x1; y1), (x2; y2) и (x3; y3), (x4; y4) не пересекаются, а отрезки с концами в точках (x3; y3), (x4; y4) и (x4; y4) и (x5; y5) имеют общую вершину, что можно считать частным случаем пересечения.
Алгоритм для определения, пересекаются ли два отрезка с концами в точках (x1; y1), (x2; y2) и (x3; y3), (x4; y4) будет следующим:
Z1:=(x3 – x1)*(y2 – y1) – (y3 – y1)*(x2 – x1)
Z2:=(x4 – x1)*(y2 – y1) – (y4 – y1)*(x2 – x1)
Z3:=(x1 – x3)*(y4 – y3) – (y1 – y3)*(x4 – x3)
Z4:=(x2 – x3)*(y4 – y3) – (y2 – y3)*(x4 – x3)
Приведенный фрагмент алгоритма не учитывает крайней ситуации, когда два отрезка лежат на одной прямой. В этом случае (x3 – x1) * (y2 – y1) – (y3 – y1) * (x2 – x1) = 0 и (x4 – x1) * (y2 – y1) – (y4 – y1) * (x2 – x1) = 0.
На рис. 5 отрезки, лежащие на одной прямой не пересекаются, а на рис. 6 – отрезки пересекаются.
Для того, чтобы определить взаимное расположение таких отрезков, поступим следующим образом. Обозначим
Здесь k1 является левой, а k2 – правой точкой проекции первого отрезка (отрезка, заданного координатами (x1; y1), (x2; y2)) на ось Ox. Аналогично k3 является левой, а k4 – правой точкой проекции второго отрезка (отрезка, заданного координатами (x3; y3), (x4; y4)) на ось Ox. Аналогично ищем преокции на ось OY.
Отрезки, лежащие на одной прямой будут пересекаться тогда, когда их проекции на каждую ось пересекаются. (Следует заметить, что если проекции двух произвольных отрезков пересекаются, то это не значит, что и сами отрезки пересекаются, что видно на рис. 7 ).
Для определения взаимного расположения проекций на ось OX воспользуемся следующим фактом (см. рис. 5 и рис. 6 ): координата левой точки пересечения проекций Lx равна max(k1; k3), т. е. максимальной из координат левых точек проекций. Рассуждая аналогично для правых точек проекций, получим, что координата правой точки Rx пересечения равна min(k2; k4). Для того, чтобы отрезки пересекались, необходимо, чтобы левая координата пересечения проекций была не больше правой координаты пересечения отрезков (такой случай имеет место на рис. 5 , когда Lx = х3, а Rx = х2). Поэтому условием пересечения проекций является выполнение неравенства Lx £ Rx. Аналогично можно вычислить величины Lу и Rу, беря соответствующие проекции на ось Оу.
Следует отметить, что длина пересечения проекций в этом случае равна величине Lx– Rx (если Lx– Rx = 0, то проекции имеют только общую точку).
1.4. Точка пересечения отрезков
Для определения места пересечения отрезков (если известно, что они пересекаются), достаточно определить точку пересечения прямых, на которых эти отрезки лежат.
Пусть A1x + B1y + C1 = 0 является уравнением прямой, проходящей через концевые точки первого отрезка, а A2x + B2y + C2 = 0 является уравнением прямой, проходящей через концевые точки второго отрезка.
Тогда для определения точки пересечения отрезков достаточно решить систему уравнений
Домножив первое уравнение на A2, а второе уравнение на A1, получим
Вычитая из первого уравнения второе, можно найти значение y:
y =
Аналогично можно вычислить значение x:
x =
Это справедливо в случае, если выражение A2 * B1 – A1 * B2 ¹ 0. Но мы уже знаем, что отрезки пересекаются и не лежат на одной прямой. А это невозможно, если A2 * B1 – A1 * B2 = 0.
2.1 Расстояния между точками. Расстояние от точки до прямой
Расстояние между точками M1(x1; y1) и M2(x2; y2) на плоскости ( рис. 8 ) определяется по формуле
D = 
Расстояние от точки до прямой на плоскости определяется как длина отрезка перпендикуляра, опущенного из точки на прямую. Уравнение вида

где T = 
Запишем алгоритм для определения расстояния от точки (x3; y3) до прямой, проходящей через точки (x1; y1) и (x2; y2).
C:= – x1*(y2 – y1)+y1*(x2 – x1) (1. 5)
Рассмотрим пример: x1 = 0, y1 = 0, x2 = 3, y2 = 4 x3 = –1, y3 = 7. Уравнение прямой, проходящей через точки (x1; y1) и (x2; y2), будет следующим:
Т = 


D = 

2.2. Расстояние между точкой и отрезком
Для определения расстояния между точкой и отрезком необходимо выяснить, пересекает ли перпендикуляр, опущенный из данной точки на прямую, проходящую через концы отрезка, сам отрезок. Если перпендикуляр пересекает отрезок, то расстояние между точкой и отрезком равно расстоянию между точкой и прямой, проходящей через отрезок. (Эту задачу вы уже умеете решать.)
Если перпендикуляр не пересекает отрезок, то расстояние между точкой и отрезком равно минимальному из расстояний между точкой и одним из концов отрезка.
Для определения взаимного расположения отрезка и перпендикуляра поступим следующим образом.
Рассмотрим треугольник, образованный тремя точками, две из которых (x1; y1) и (x2; y2) являются концами данного отрезка, а третья – данная точка с координатами (x3; y3) (см. рис. 10 , б, в). Конечно, может оказаться, что все точки лежат на одной прямой и такого треугольника не существует. В этом случае, однако, мы будем полагать, что треугольник существует, правда он вырожденный (особый). В вырожденном треугольнике длины сторон могут быть равными 0 (см. рис. 10 , а).
Более того, мы будем полагать, что данный отрезок является основанием рассматриваемого треугольника (см. рис. 10 , б, в).
При таких предположениях для решения исходной задачи нам достаточно определить, является ли один из углов при основании тупым или нет. Действительно, если один из углов при основании является тупым, то перпендикуляр, опущенный из вершины, соответствующей исходной точке, не попадает на основание (отрезок). Иначе перпендикуляр, опущенный из вершины, соответствующей исходной точке, попадает на основание (отрезок).
Для решения последней задачи воспользуемся следующим свойством. Пусть a, b, c – длины сторон треугольника, причем с – длина основания. Тогда треугольник является тупоугольным при основании, если
Поэтому, вычислив значения квадратов длин сторон, нетрудно определить, пересекает ли перпендикуляр, опущенный из точки (x3; y3) на прямую, отрезок с концами в точках (x1; y1) и (x2; y2). И если не пересекает, то расстояние от точки до отрезка равно минимуму из величин a, b. Если же пересекает, то необходимо воспользоваться свойством нормального уравнения прямой .
§ 3. Многоугольники
3.1. Виды многоугольников
Ломаной называется фигура, которая состоит из точек A1, A2, . An и соединяющих их отрезков A1A2, A2A3, . An – 1An ( рис. 11 , а). Точки называются вершинами ломаной, а отрезки – звеньями. Наиболее распространенным способом задания ломаной является использование таблицы, элементы которой соответствуют координатам вершин ломаной в порядке ее обхода из одного конца в другой. Длиной ломаной называется сумма длин ее звеньев.
Многоугольником называется замкнутая ломаная линия без самопересечений (рис. 11, б).
Плоским многоугольником называется конечная часть плоскости, ограниченная многоугольником (рис. 11, в).
Обход плоского многоугольника называется положительным, если при обходе область расположена по левую руку, и отрицательным, если область остается по правую руку.
Расстояние между фигурами на плоскости определяется как длина минимального отрезка, один конец которого принадлежит одной фигуре, а второй конец – другой фигуре.
3.2. Выпуклость многоугольников
Многоугольник является выпуклым, если для каждой прямой, проходящей через любую его сторону, все остальные вершины лежат в одной полуплоскости относительно прямой. Проверим для каждой прямой, проходящей через вершины (x1; y1) и (x2; y2), (x2; y2) и (x3; y3), . (xn – 1; yn – 1) и (xn; yn), (xn; yn) и (x1; y1) взаимное расположение вершин многоугольника. Если они каждый раз расположены в одной полуплоскости относительно проведенной прямой, то многоугольник выпуклый. Если же найдется прямая, проходящая через одну из сторон, и пара вершин многоугольника, лежащих по разные стороны относительно проведенной прямой, то многоугольник не является выпуклым. Случаи выпуклого и невыпуклого многоугольников изображены на рис. 12.
Можно заметить, что для каждой прямой, проходящей через вершины (x1; y1) и (x2; y2), (x2; y2) и (x3; y3), . (xn – 1; yn – 1) и (xn; yn), (xn; yn) и (x1; y1) достаточно ограничится определением взаимного расположения вершин многоугольника (xn; yn) и (x3; y3), (x1; y1) и (x4; y4), . (xn – 2; yn – 2) и (x1; y1), (xn – 1; yn – 1) и (x2; y2), соответственно. Если они каждый раз расположены в одной полуплоскости относительно проведенной прямой, то многоугольник выпуклый. Если же найдется прямая и пара вершин многоугольника, лежащих по разные стороны относительно проведенной прямой, то многоугольник не является выпуклым. Поэтому для определения, является ли многоугольник выпуклым, достаточно воспользоваться алгоритмом
нц для i от 1 до n
½ j:= mod( i, n +1 ) : номер вершины после вершины i
½ k:= mod (j, n +1) : номер вершины после вершины j
½½ то m:=n : номер вершины перед вершиной i
Видео:Уравнение прямой, проходящей через точку параллельно OX, OY или через начало координат. Урок 5. 8 клСкачать

Линейная функция — определение и вычисление с примерами решения
Содержание:
Рассмотрим уравнение с двумя неизвестными
где 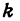
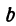
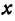
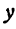
удовлетворяют следующие пары:
Для того чтобы найти пару чисел, удовлетворяющих уравнению 

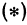

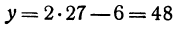
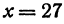
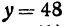
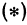


Так как в данном уравнении 

Для 


Функцию 
Пример:
Вычислить значения линейной функции, определяемой уравнением 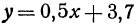
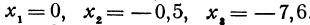
Решение:
Если 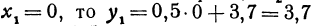
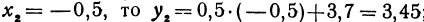
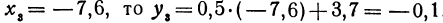
Покажем, что если принять пару чисел 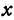
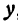
В самом деле, рассмотрим точку 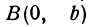
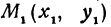
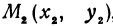
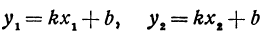
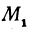
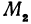
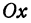
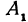
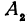
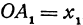

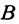
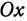
Предположим, что точки 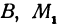
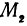
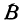
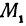
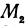
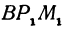
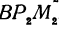
Но так как 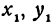
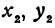
Выражения 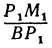
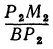
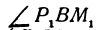
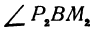
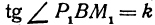
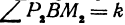

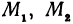
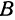
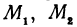
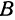
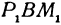
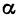
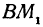
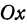
Так как 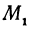
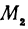
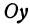
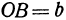
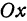
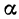
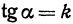
Число 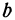
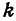
Предыдущие рассуждения позволяют сделать вывод: линейная функция 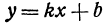
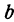
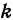
Например, линейная функция 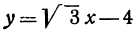
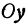
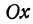
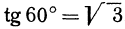
Если имеем определенную прямую, отсекающую на оси 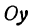
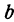
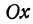
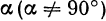
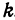
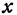
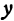
Очевидно, имеет место и такое предложение: Всякой прямой, отсекающей на оси 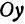
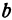
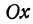
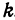
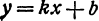
Координаты любой, точки, лежащей на указанной прямой, удовлетворяют уравнению (1), поэтому уравнение 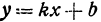
Таким образом, всякая линейная функция является уравнением некоторой прямой.
Отметим частные случаи.
1. Пусть 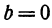
Прямая, определяемая этим уравнением, проходит через начало координат. Здесь 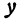
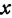
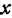
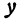
2. Пусть 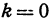
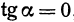
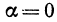
Этому уравнению соответствует прямая, параллельная оси 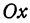
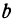
На основании всего сказанного в этом параграфе легко решаются следующие задачи.
Пример:
Даны точки 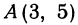
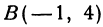
Решение:
Если точка лежит на прямой, то ее координаты должны удовлетворять уравнению прямой. Поэтому для решения задачи подставим координаты точки 
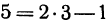
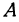
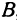
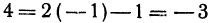
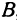
Пример:
Построить прямую, уравнение которой
Решение:
Чтобы построить прямую, надо знать, например, две ее точки. Поэтому дадим 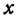
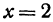
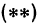
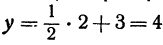
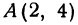
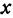
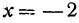
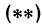
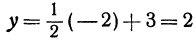
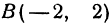
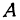
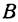
Видео:§51 Уравнение прямой в пространстве, проходящей через две точкиСкачать

Основное свойство линейной функции
Рассмотрим линейную функцию 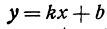
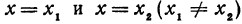
Здесь первое и второе значения 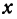
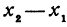

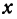
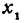
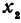
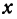
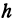
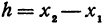
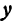
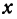
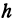
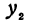
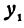
т. е. приращение линейной функции пропорционально приращению независимого переменного.
Это и есть основное свойство линейной функции.
Заметим, что 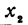
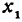
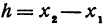
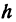
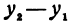
Пример:
Найдем приращение функции 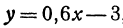
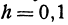
Решение:
По основному свойству 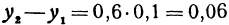
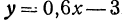
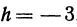
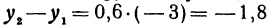
Пример:
Найдем приращение функции 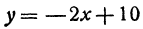
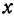

Задачи на прямую
Пример:
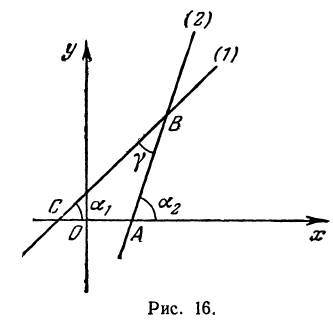
Найти угол 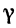
Решение:
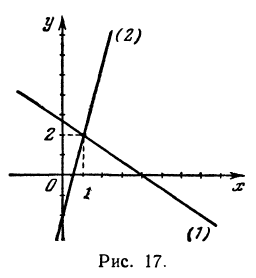
При пересечении прямых образуются четыре попарно равных угла. Найдя один из них, легко найти и другие. На рис. 16 прямые обозначены соответственно (1) и (2).
Угол 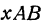
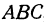
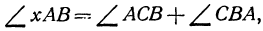
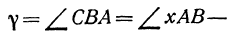
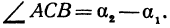
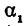
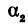
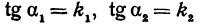
Пример:
Найти угол между прямыми, заданными уравнениями 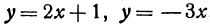
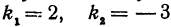
Решение:
Применяя формулу (1), получим:
Если же будем считать, что 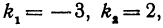
Получены два ответа: сначала найден острый угол между заданными прямыми, а затем — тупой.
Если заданы две параллельные прямые, то углы 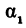
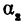
Таким образом, мы приходим к выводу: если прямые параллельны, то их угловые коэффициенты равны.
Если прямые перпендикулярны, то угол между ними равен 90°, т. е. 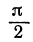
Это и есть условие перпендикулярности двух прямых. Это условие удобно запомнить в следующей формулировке: если две прямые перпендикулярны, то их угловые коэффициенты обратны по величине и противоположны по знаку.
Пример:
Найдем угол между прямыми, заданными уравнениями 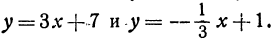
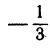
Решение:
Следовательно, рассматриваемые прямые перпендикулярны.
Пример:
Даны две точки: 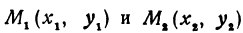
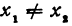
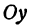
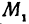
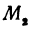
Решение:
Искомая прямая не параллельна оси 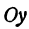
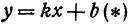
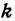
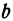
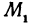
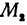
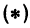
В уравнениях 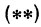
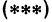
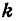
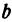
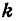
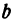
Решая систему, находим:
Подставляя найденные выражения в уравнение 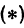
Это и есть уравнение прямой, проходящей через две точки, не расположенные на прямой, параллельной оси 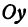
Пример:
Написать уравнение прямой, проходящей через данную точку 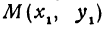
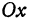
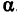
Решение:
Прежде всего найдем угловой коэффициент искомой прямой: он равен тангенсу угла 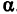
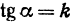
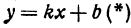
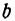
Так как прямая должна проходить через точку 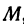
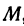
Находим отсюда неизвестное 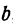
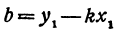
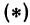
Это и есть уравнение прямой, проходящей через точку 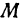
Если в уравнении (4) менять направление, не меняя точку 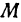
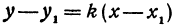
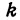
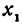
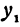
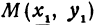
Пример:
Напишем уравнение прямой, проходящей через точку 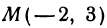
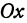
Решение:
Так как 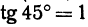
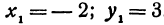
Общее уравнение прямой. Неявная линейная функция
Рассмотрим уравнение первой степени с двумя неизвестными
Решим его относительно 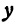
т. е. мы получили линейную функцию, где 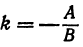
Уравнения (1) и (2) равносильны, поэтому пара чисел 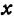
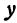
Координаты любой точки, лежащей на этой прямой, удовлетворяют уравнению (1), поэтому будем называть его также уравнением прямой. Рассмотрим особо случай, когда 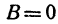
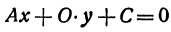
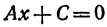
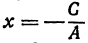
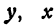
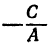
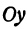
Из уравнения (1) (если 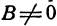
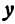
Система двух уравнений первой степени
Напомним, что две прямые, расположенные на плоскости, могут или пересекаться, или быть параллельными (т. е. не пересекаться), или сливаться (в этом случае можно сказать, что они пересекаются в каждой своей точке). Рассмотрим систему двух уравнений
Каждое из этих уравнений является уравнением прямой. Решить систему — это значит найти значения 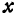
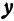
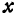
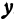
Пример:
Найдем точку пересечения двух прямых:
Решение:
Решая эту систему, получим: 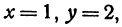
Пример:
Найдем точку пересечения двух прямых:
Решение:
Решая эту систему, получим: 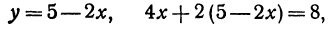
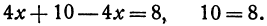
Пример:
Найдем точку пересечения данных прямых
Решение:
Решая эту систему, получим:
Полученное равенство всегда справедливо, т. е. справедливо при любом значении 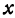
Заметим, что два уравнения, рассматриваемые в этом примере, являются равносильными, поэтому они и представляют одну и ту же прямую.
Примеры применения линейной функции
Линейная функция встречается в формулировках многих физических законов и технических задач. Приведем примеры.
Пример:
Если точка движется равномерно по прямой, то ее расстояние от выбранной точки (от начала координат) выражается при помощи уравнения 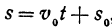
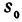
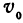
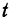
Пример:
Закон Ома записывается в виде 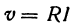
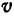
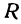
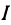
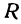
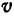
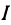
Пример:
Если стоимость провоза единицы товара по железной дороге равна 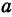
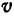
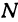
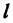
Если же стоимость товара на месте равна 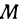
Здесь 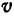
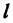
Линейная функция встречается в различных областях, но, где бы она ни встречалась, ее всегда можно рассматривать как уравнение прямой. Этим обстоятельством часто пользуются при решении задач.
Пример:
Два города А и В, расстояние между которыми равно 300 км, находятся на одной железнодорожной магистрали. На этой же магистрали между городами А к В надо выбрать пункт С, в котором предполагается устроить склад нефти для снабжения указанных городов. Надо выбрать пункт С так, чтобы общая стоимость перевозок нефти для снабжения города А и города В была наименьшей. Известно, что город А потребляет 400 т нефти, а город В —200 т. Перевозка одной тонны нефти на один километр обходится в 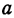
Решение:
Обозначим расстояние от А до предполагаемого пункта С через 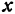
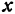
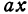
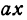
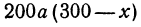
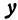
Это линейная функция. Если примем 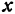
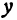
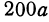
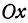
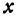
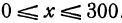
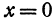
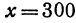
Так как пункт С надо выбрать так, чтобы стоимость была наименьшей, то его следует расположить в городе А; если же этого сделать нельзя по каким-либо соображениям, то, чем ближе расположить его к А, тем выгодней.
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Квадратичная функция
- Тригонометрические функции
- Производные тригонометрических функции
- Производная сложной функции
- Функции нескольких переменных
- Комплексные числ
- Координаты на прямой
- Координаты на плоскости
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Telegram и логотип telegram являются товарными знаками корпорации Telegram FZ-LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Видео:Составить уравнение прямой, проходящей через две данные точки. Метод координат. Геометрия 9 классСкачать

Практика. Решение задач. Часть 1. Уравнения прямой
Этот видеоурок доступен по абонементу
У вас уже есть абонемент? Войти
Мы изучили новые инструменты – координаты и действия с векторами в координатах, операцию скалярного умножения векторов. Этот урок мы посвятим решению задач и потренируемся применять эти новые инструменты на практике.
🌟 Видео
11. Прямая в пространстве и ее уравненияСкачать

УРАВНЕНИЕ ПРЯМОЙСкачать
Как составить уравнение прямой, проходящей через две точки. Урок 3. Геометрия 8 класс.Скачать

Уравнение прямойСкачать

§11 Уравнение прямой, проходящей через две точки на плоскостиСкачать

Аналитическая геометрия, 6 урок, Уравнение прямойСкачать

Уравнение прямой. Видеоурок 6. Геометрия 9 классСкачать

КООРДИНАТНАЯ ПРЯМАЯСкачать

Видеоурок "Уравнение прямой с угловым коэффициентом"Скачать