Если ранг совместной системы линейных уравнений с 5 переменными равен 3 то число базисных

Что означает фраза «ранг матрицы равен $r$»? Она означает, что есть хотя бы один минор $r$-го порядка, который не равен нулю. Напомню, что такой минор называется базисным. Базисных миноров может быть несколько. При этом все миноры, порядок которых выше $r$, равны нулю или не существуют.

Выбрать $r$ базисных переменных в общем случае можно различными способами. В примерах я покажу наиболее часто используемый способ выбора.

Во всех изложенных ниже примерах матрицу системы будем обозначать буквой $A$, а расширенную матрицу системы – буквой $widetilde$.

Решить СЛАУ $ left < begin& 3x_1-6x_2+9x_3+13x_4=9\ & -x_1+2x_2+x_3+x_4=-11;\ & x_1-2x_2+2x_3+3x_4=5. end right.$. Если система является неопределённой, указать базисное решение.

Итак, мы имеем СЛАУ, у которой 3 уравнения и 4 переменных: $x_1$, $x_2$, $x_3$, $x_4$. Так как количество переменных больше количества уравнений, то такая система не может иметь единственное решение (чуть позже мы строго докажем это предложение на основе теоремы Кронекера-Капелли). Найдём решения СЛАУ, используя метод Гаусса:

$$ left( begin 3 & -6 & 9 & 13 & 9 \ -1 & 2 & 1 & 1 & -11 \ 1 & -2 & 2 & 3 & 5 end right) rightarrow left|begin & text\ & text\ & text endright| rightarrow \ rightarrowleft( begin 1 & -2 & 2 & 3 & 5\ -1 & 2 & 1 & 1 & -11 \ 3 & -6 & 9 & 13 & 9 end right) begin phantom \ II+I\ III-3cdot Iend rightarrow left( begin 1 & -2 & 2 & 3 & 5\ 0 & 0 & 3 & 4 & -6 \ 0 & 0 & 3 & 4 & -6 endright) begin phantom \ phantom\ III-IIend rightarrow \ rightarrowleft( begin 1 & -2 & 2 & 3 & 5\ 0 & 0 & 3 & 4 & -6 \ 0 & 0 & 0 & 0 & 0 endright) $$

Мы завершили прямой ход метода Гаусса, приведя расширенную матрицу системы к ступенчатому виду. Слева от черты расположены элементы преобразованной матрицы системы, которую мы также привели к ступенчатому виду. Напомню, что если некая матрица приведена к ступенчатому виду, то её ранг равен количеству ненулевых строк.

И матрица системы, и расширенная матрица системы после эквивалентных преобразований приведены к ступенчатому виду; они содержат по две ненулевых строки. Вывод: $rang A=rangwidetilde = 2$.

Итак, заданная СЛАУ содержит 4 переменных (обозначим их количество как $n$, т.е. $n=4$). Кроме того, ранги матрицы системы и расширенной матрицы системы равны между собой и равны числу $r=2$. Так как $r < n$, то согласно следствию из теоремы Кронекера-Капелли СЛАУ является неопределённой (имеет бесконечное количество решений).

Найдём эти решения. Для начала выберем базисные переменные. Их количество должно равняться $r$, т.е. в нашем случае имеем две базисные переменные. Какие именно переменные (ведь у нас их 4 штуки) принять в качестве базисных? Обычно в качестве базисных переменных берут те переменные, которые расположены на первых местах в ненулевых строках преобразованной матрицы системы, т.е. на «ступеньках». Что это за «ступеньки» показано на рисунке:

На «ступеньках» стоят числа из столбцов №1 и №3. Первый столбец соответствует переменной $x_1$, а третий столбец соответствует переменной $x_3$. Именно переменные $x_1$ и $x_3$ примем в качестве базисных.

В принципе, если вас интересует именно методика решения таких систем, то можно пропускать нижеследующее примечание и читать далее. Если вы хотите выяснить, почему можно в качестве базисных взять именно эти переменные, и нельзя ли выбрать иные – прошу раскрыть примечание.

Почему можно принять переменные $x_1$ и $x_3$ в качестве базисных? Для ответа на этот вопрос давайте вспомним, что ранг матрицы системы равен числу $r=2$. Это говорит о том, что все миноры данной матрицы, порядок которых выше 2, либо равны нулю, либо не существуют. Ненулевые миноры есть только среди миноров второго порядка. Выберем какой-либо ненулевой минор второго порядка. Мы можем выбирать его как в исходной матрице системы $A$, т.е. в матрице $left( begin 3 & -6 & 9 & 13 \ -1 & 2 & 1 & 1 \ 1 & -2 & 2 & 3 end right)$, так и в преобразованной матрице системы, т.е. в $left( begin 1 & -2 & 2 & 3 \ 0 & 0 & 3 & 4 \ 0 & 0 & 0 & 0 endright)$. Так как в преобразованной матрице системы побольше нулей, то будем работать именно с нею.

Итак, давайте выберем минор второго порядка, элементы которого находятся на пересечении строк №1 и №2, и столбцов №1 и №2:

$$ M_^=left| begin 1 & -2 \ 0 & 0 endright|=1cdot 0-(-2)cdot 0=0. $$

Вывод: выбранный нами минор второго порядка не является базисным, ибо он равен нулю. Так как элементы этого минора взяты из столбца №1 (он соответствует переменной $x_1$) и столбца №2 (он соответствует переменной $x_2$), то пара переменных $x_1$ и $x_2$ не могут быть базисными переменными.

Осуществим вторую попытку, взяв минор второго порядка, элементы которого лежат на пересечении строк №1, №2 и столбцов №3 и №4:

$$ M_^=left| begin 2 & 3\ 3 & 4 endright|=2cdot 4-3cdot 3=-1. $$

Вывод: выбранный нами минор второго порядка является базисным, ибо он не равен нулю. Так как элементы этого минора взяты из столбца №3 (он соответствует переменной $x_3$) и столбца №4 (он соответствует переменной $x_4$), то пару переменных $x_3$ и $x_4$ можно принять в качестве базисных.

Сделаем и третью попытку, найдя значение минора, элементы которого расположены на пересечении строк №1, №2 и столбцов №1 и №3:

Вывод: выбранный нами минор второго порядка является базисным, ибо он не равен нулю. Так как элементы этого минора взяты из столбца №1 (он соответствует переменной $x_1$) и столбца №3 (он соответствует переменной $x_3$), то пару переменных $x_1$ и $x_3$ можно принять в качестве базисных.

Как видите, выбор базисных переменных не является однозначным. На самом деле количество вариантов выбора не превышает количество размещений из $n$ элементов по $r$, т.е. не больше чем $C_^$.

В рассматриваемом примере в качестве баисных были приняты переменные $x_1$ и $x_3$ – сугубо из соображений удобства дальнейшего решения. В чём это удобство состоит, будет видно чуток позже.

Базисные переменные выбраны: это $x_1$ и $x_3$. Остальные $n-r=2$ переменных (т.е. $x_2$ и $x_4$) являются свободными. Нам нужно выразить базисные переменные через свободные.

Я предпочитаю работать с системой в матричной форме записи. Для начала очистим полученную матрицу $left( begin 1 & -2 & 2 & 3 & 5\ 0 & 0 & 3 & 4 & -6 \ 0 & 0 & 0 & 0 & 0 endright)$ от нулевой строки:

$$ left( begin 1 & -2 & 2 & 3 & 5\ 0 & 0 & 3 & 4 & -6 endright) $$

Свободным переменным, т.е. $x_2$ и $x_4$, соответствуют столбцы №2 и №4. Перенесём эти столбцы за черту. Знак всех элементов переносимых столбцов изменится на противоположный:

Почему меняются знаки? Что вообще значит это перенесение столбцов? показатьскрыть

Давайте обратимся к расширенной матрице системы, которая после преобразований имеет вид $left( begin 1 & -2 & 2 & 3 & 5\ 0 & 0 & 3 & 4 & -6 endright)$. Перейдём от матрицы к уравнениям. Первая строка соответствует уравнению $x_1-2x_2+2x_3+3x_4=5$, а вторая строка соответствует уравнению $3x_3+4x_4=-6$. Теперь перенесём свободные переменные $x_2$ и $x_4$ в правые части уравнений. Естественно, что когда мы переносим выражение $4x_4$ в правую часть уравнения, то знак его изменится на противоположный, и в правой части появится $-4x_4$.

Если опять записать полученную систему в виде матрицы, то мы и получим матрицу с перенесёнными за черту столбцами.

А теперь продолжим решение обычным методом Гаусса. Наша цель: сделать матрицу до черты единичной. Для начала разделим вторую строку на 3, а потом продолжим преобразования обратного хода метода Гаусса:

$$ left( begin 1 & 2 & 5 & 2 & -3\ 0 & 3 & -6 & 0 & -4 endright) begin phantom \ II:3 end rightarrow left( begin 1 & 2 & 5 & 2 & -3\ 0 & 1 & -2 & 0 & -4/3 endright) begin I-2cdot II \ phantom end rightarrow \ rightarrow left(begin 1 & 0 & 9 & 2 & -1/3\ 0 & 1 & -2 & 0 & -4/3 endright). $$

Матрица до черты стала единичной, метод Гаусса завершён. Общее решение найдено, осталось лишь записать его. Если вспомнить, что четвёртый столбец соответствует переменной $x_2$, а пятый столбец – переменной $x_4$, то получим:

Нами получено общее решение заданной СЛАУ. Чтобы найти базисное решение, нужно все свободные переменные приравнять к нулю. Т.е. полагая $x_2=0$ и $x_4=0$, будем иметь:

Решение $x_1=9$, $x_2=0$, $x_3=-2$, $x_4=0$ и является базисным решением данной СЛАУ. В принципе, задавая свободным переменным иные значения, можно получить иные частные решения данной системы. Таких частных решений бесконечное количество. Например, принимая $x_2=-4$ и $x_4=1$, получим такое частное решение: $left <begin& x_1=frac;\ & x_2=-4;\ & x_3=-frac;\ & x_4=1. endright.$. Базисное решение, которые мы нашли ранее – лишь одно из бесконечного множества частных решений заданной СЛАУ.

Если есть желание, то полученное решение можно проверить. Например, подставляя $x_1=9+2x_2-fracx_4$ и $x_3=-2-fracx_4$ в левую часть первого уравнения, получим:

$$ 3x_1-6x_2+9x_3+13x_4=3cdot left(9+2x_2-fracx_4right)-6x_2+9cdot left(-2-fracx_4right)+13x_4=9. $$

Проверка первого уравнения увенчалась успехом; точно так же можно проверить второе и третье уравнения.

Если система является неопределённой, указать базисное решение.

Похожий пример уже был решен в теме «метод Крамера» (пример №4). Переменные $x_4$ и $x_5$ были перенесены в правые части, а дальше применялись стандартные операции метода Крамера. Однако такой метод решения не гарантирует достижения результата. Например, мы переносим некие переменные в правую часть, а оставшийся определитель оказывается равным нулю, – что тогда? Решать перебором? 🙂 Поэтому гораздо удобнее применять преобразования метода Гаусса, как и в предыдущем примере.

$$ left( begin 1 & -2 & 4 & 0 & 2 & 0\ 4 & -11 & 21 & -2 & 3 & -1\ -3 & 5 & -13 & -4 & 1 & -2 end right) begin phantom \ II-4cdot I\ III+3cdot Iend rightarrow left( begin 1 & -2 & 4 & 0 & 2 & 0\ 0 & -3 & 5 & -2 & -5 & -1\ 0 & -1 & -1 & -4 & 7 & -2 end right) rightarrow \ rightarrow left|begin & text\ & text\ & text endright|rightarrow left( begin 1 & -2 & 4 & 0 & 2 & 0\ 0 & -1 & -1 & -4 & 7 & -2\ 0 & -3 & 5 & -2 & -5 & -1 end right) begin phantom \ phantom\ III-3cdot Iend rightarrow \ rightarrow left( begin 1 & -2 & 4 & 0 & 2 & 0\ 0 & -1 & -1 & -4 & 7 & -2\ 0 & 0 & 8 & 10 & -26 & 5 end right). $$

Матрица системы и расширенная матрица системы приведены к трапециевидной форме. Ранги этих матриц равны между собой и равны числу 3, т.е. $rang A=rangwidetilde = 3$. Так как ранги равны между собой и меньше, чем количество переменных, то согласно следствию из теоремы Кронекера-Капелли данная система имеет бесконечное количество решений.

Количество неизвестных $n=5$, ранги обеих матриц $r=3$, поэтому нужно выбрать три базисных переменных и $n-r=2$ свободных переменных. Применяя тот же метод «ступенек», что и в предыдущем примере, выберем в качестве базисных переменных $x_1$, $x_2$, $x_3$, а в качестве свободных переменных – $x_4$ и $x_5$.

Столбцы №4 и №5, которые соответствуют свободным переменным, перенесём за черту. После этого разделим третью строку на 8 и продолжим решение методом Гаусса:

$$ left( begin 1 & -2 & 4 & 0 & 0 & -2\ 0 & -1 & -1 & -2 & 4 & -7\ 0 & 0 & 8 & 5 & -10 & 26 end right) begin phantom \ phantom\ III:8end rightarrow left( begin 1 & -2 & 4 & 0 & 0 & -2\ 0 & -1 & -1 & -2 & 4 & -7\ 0 & 0 & 1 & 5/8 & -5/4 & 13/4 end right) begin I-4cdot III \ II+III\ phantomend rightarrow \ left( begin 1 & -2 & 0 & -5/2 & 5 & -15\ 0 & -1 & 0 & -11/8 & 11/4 & -15/4\ 0 & 0 & 1 & 5/8 & -5/4 & 13/4 end right) begin phantom \ IIcdot (-1)\ phantomend rightarrow left( begin 1 & -2 & 0 & -5/2 & 5 & -15\ 0 & 1 & 0 & 11/8 & -11/4 & 15/4\ 0 & 0 & 1 & 5/8 & -5/4 & 13/4 end right) begin I+2cdot II \ phantom\ phantomend rightarrow\ rightarrowleft( begin 1 & 0 & 0 & 1/4 & -1/2 & -15/2\ 0 & 1 & 0 & 11/8 & -11/4 & 15/4\ 0 & 0 & 1 & 5/8 & -5/4 & 13/4 end right) $$

Продолжение этой темы рассмотрим во второй части, где разберём ещё два примера с нахождением общего решения.

Видео:Система линейных уравнений. Общее решение. Метод ГауссаСкачать

Критерий совместности систем линейных уравнений

Тема 2. Системы линейных уравнений

Критерий совместности систем линейных уравнений

Система m линейных уравнений c n неизвестными имеет вид:

(2.1)

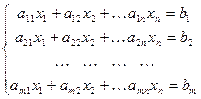
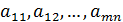
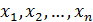
Здесь – коэффициенты системы, – свободные члены, а — неизвестные вещественные числа. Используя понятие произведения матриц, можно переписать систему (2.1) в матричном виде:

где A = (а_ij) — матрица, состоящая из коэффициентов при неизвестных системы (2.1), которая называется матрицей системы, X = (x₁, x₂. x_n) T ,
B = (b₁, b₂. b_m) T — векторы-столбцы, составленные соответственно из неизвестных x_j и из свободных членов b_i.

Система называется однородной, если все ее свободные члены равны нулю: b_i=0 для всех i.

Если хотя бы один из свободных членов отличен от нуля, система называется неоднородной.

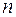
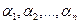
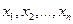
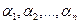
Совокупность чисел называется решениемсистемы (2.1), если после замены неизвестных числами соответственно каждое из уравнений системы превращается в верное равенство

Система (2.1) называется совместной, или разрешимой, если она имеет по крайней мере одно решение. Система называется несовместной, или неразрешимой, если она не имеет решений.

= ,

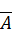
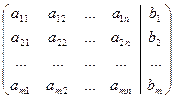
образованная путем приписывания справа к матрице 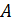столбца свободных членов, называется расширенной матрицей системы.

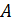
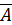
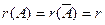
Теорема Кронекера- Капелли. Система линейных уравнений (2.1) совместна тогда и только тогда, когда ранги матриц и совпадают, т.е.
.

Для множества решений системы (2.1) имеются три возможности:

1) Если 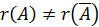, решений нет. В этом случае система несовместна.

2) Если 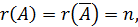cистема имеет единственное решение. В этом случае система называется определенной.

3) Если 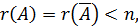cистема имеет бесчисленное множество решений. В этом случае система называется неопределенной.

Рассмотрим более подробно случай неопределенной системы. Предположим, что базисный минор матрицы находится в левом верхнем углу расширенной матрицы (всегда можно перенумеровать неизвестные и поменять местами строки, чтобы это было верно). Если ранг расширенной матрицы системы равен r, то первые r ее строк являются базисными. По теореме о базисном миноре каждая из строк расширенной матрицы, начиная с (r+1)-ой строки, является линейной комбинацией первых r строк этой матрицы. Это означает, что каждое из уравнений системы (2.1), начиная с (r+1)-го уравнения, является линейной комбинацией первых r уравнений этой системы. 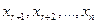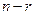Придавая неизвестным совершенно произвольные значения, достаточно найти r неизвестных из первых r уравнений системы. Таким образом, в случае неопределенной системы переменных, которые называются базисными переменными, выражаются через ( ) переменных, которые называются свободными переменными.

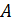
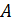
Универсальным методом решения систем линейных уравнений является метод Гаусса, или метод исключения неизвестных. В частном случае, когда матрица системы квадратная и ее определитель отличен от нуля det( ) , можно использовать для нахождения решения либо метод Крамера, либо матричный метод.

Пример 2.1. Исследовать систему уравнений на совместность:

Решение.Выписываем расширенную матрицу системы:

= .

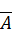
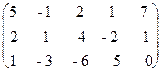
Вычислим ранг основной матрицы системы. Очевидно, что, например, минор второго порядка в левом верхнем углу 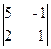= 7 ¹ 0; содержащие его миноры третьего порядка равны нулю:

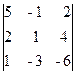
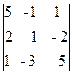
M¢₃ = = 0, M²₃ = = 0.

Следовательно, ранг основной матрицы системы равен 2, т.е. r(A)=2. Для вычисления ранга расширенной матрицы `A рассмотрим окаймляющий минор

= = -35 ¹ 0,

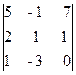
значит, ранг расширенной матрицы r( 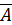) = 3. Поскольку r(A) ¹ r( ), то система несовместна.

Дата добавления: 2015-09-29 ; просмотров: 3105 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Видео:Математика без Ху!ни. Метод Гаусса. Совместность системы. Ранг матрицы.Скачать

Решение задач по математике онлайн

//mailru,yandex,google,vkontakte,odnoklassniki,instagram,wargaming,facebook,twitter,liveid,steam,soundcloud,lastfm, // echo( ‘

Видео:Исследование систем линейных уравнений на совместностьСкачать

Калькулятор онлайн.
Решение систем линейных алгебраических уравнений (СЛАУ)
Метод Гаусса, матричный метод, метод Крамера, исследование на совместность (теорема Кронекера-Капелли), определение количества решений, нахождение нормальной фундаментальной системы решений.

С помощью данной математической программы вы можете решить и исследовать систему линейных алгебраических уравнений (СЛАУ).

Программа не только даёт ответ задачи, но и приводит подробное решение с пояснениями шагов решения.

Данная программа может быть полезна учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.

Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.

Ввод дробного числа в виде десятичной дроби.
При вводе десятичной дроби, целую часть от дробной части можно отделять точкой или запятой :
Ввод: -2.34
Результат: ( -234 )

Ввод: -1,15
Результат: ( -115 )

Ввод дробного числа в виде обыкновенной дроби.
В качестве числителя, знаменателя и целой части дроби может выступать только целое число.
Знаменатель не может быть отрицательным.

При вводе числовой дроби числитель отделяется от знаменателя знаком деления: /
Ввод: -2/3
Результат: $$ -frac $$

Целая часть отделяется от дроби знаком амперсанд: &
Ввод: 5&8/3
Результат: $$ 5frac $$
Помните, что на ноль делить нельзя!

RND CFracNum Fill RND int Fill Start MathJax
Сюда ввести строку с GET параметрами :

Видео:Базисные решения систем линейных уравнений (01)Скачать

Немного теории.

Видео:Решение системы уравнений методом Гаусса. Бесконечное множество решенийСкачать

Системы линейных алгебраических уравнений

Основные определения

Система (m) линейных алгебраических уравнений с (n) неизвестными (сокращенно СЛАУ) представляет собой систему вида
( left< begin a_x_1 + a_x_2 + cdots + a_x_n = b_1 \ a_x_1 + a_x_2 + cdots + a_x_n = b_2 \ cdots \ a_x_1 + a_x_2 + cdots + a_x_n = b_m end right. tag )

Уравнения системы называют алгебраическими потому, что левая часть каждого из них есть многочлен от (n) переменных ( x_1 , ldots x_n ), а линейными потому, что эти многочлены имеют первую степень.

Числа (a_ in mathbb ) называют коэффициентами СЛАУ. Их нумеруют двумя индексами: номером уравнения (i) и номером неизвестного (j). Действительные числа ( b_1 , ldots b_m ) называют свободными членами уравнений.

СЛАУ называют однородной, если ( b_1 = b_2 = ldots = b_m = 0 ). Иначе её называют неоднородной.

Решением СЛАУ, да и вообще всякой системы уравнений, называют такой набор значений неизвестных ( x_1^circ, ldots , x_n^circ ), при подстановке которых каждое уравнение системы превращается в тождество. Любое конкретное решение СЛАУ также называют её частным решением.

Решить СЛАУ — значит решить две задачи:
— выяснить, имеет ли СЛАУ решения;
— найти все решения, если они существуют.

СЛАУ называют совместной, если она имеет какие-либо решения. В противном случае её называют несовместной. Однородная СЛАУ всегда совместна, поскольку нулевой набор значений её неизвестных всегда является решением.

Если СЛАУ (1) имеет решение, и притом единственное, то её называют определенной, а если решение неединственное — то неопределенной. При (m=n), т.е. когда количество уравнений совпадает с количеством неизвестных, СЛАУ называют квадратной.

Формы записи СЛАУ

Кроме координатной формы (1) записи СЛАУ часто используют и другие её представления.

Рассматривая коэффициенты (a_) СЛАУ при одном неизвестном (x_j) как элементы столбца, а (x_j) как коэффициент, на который умножается столбец, из (1) получаем новую форму записи СЛАУ:
( begin a_ \ a_ \ vdots \ a_ end x_1 + begin a_ \ a_ \ vdots \ a_ end x_2 + ldots + begin a_ \ a_ \ vdots \ a_ end x_n = begin b_1 \ b_2 \ vdots \ b_m end )
или, обозначая столбцы соответственно ( a_1 , ldots , a_n , b ),
( x_1 a_1 + x_2 a_2 + ldots + x_n a_n = b tag )

Таким образом, решение СЛАУ (1) можно трактовать как представление столбца (b) в виде линейной комбинации столбцов ( a_1, ldots, a_n ). Соотношение (2) называют векторной записью СЛАУ.

Поскольку (A ;,; X) и (B) являются матрицами, то запись СЛАУ (1) в виде (AX=B) называют матричной. Если (B=0), то СЛАУ является однородной и в матричной записи имеет вид (AX=0).

Приведенные рассуждения показывают, что задачи :
а) решения СЛАУ (1)
б) представления столбца в виде линейной комбинации данных столбцов
в) решения матричных уравнений вида (AX=B)
являются просто различной формой записи одной и той же задачи.

Критерий совместности СЛАУ

«Триединство» форм записи СЛАУ позволяет легко получить критерий совместности СЛАУ. Напомним, что содержательный смысл это понятие имеет для неоднородных СЛАУ (однородные СЛАУ всегда совместны).

Матрицу
( A = begin a_ & a_ & cdots & a_ \ a_ & a_ & cdots & a_ \ vdots & vdots & ddots & vdots \ a_ & a_ & cdots & a_ end )
называют матрицей (коэффициентов) СЛАУ (1), а матрицу
( (A|B) = left( begin a_ & a_ & cdots & a_ & b_1 \ a_ & a_ & cdots & a_ & b_2 \ vdots & vdots & ddots & vdots & vdots \ a_ & a_ & cdots & a_ & b_m end right) )
расширенной матрицей СЛАУ (1). Расширенная матрица полностью характеризует СЛАУ. Это означает, что по этой матрице однозначно (если сохранить обозначения для неизвестных) восстанавливается сама СЛАУ.

Теорема Кронекера-Капелли. Для совместности СЛАУ (AX=B) необходимо и достаточно, чтобы ранг её матрицы (A) был равен рангу её расширенной матрицы ( (A|B) ).

Формулы Крамера

Теорема. СЛАУ с квадратной невырожденной матрицей имеет решение, и притом единственное, которое определяется по формулам Крамера :
$$ x_i = frac ;,quad i=overline tag $$
где (Delta_i) — определитель матрицы, получающейся из матрицы (A) заменой (i)-го столбца на столбец свободных членов.

Следствие. Однородная СЛАУ с квадратной невырожденной матрицей имеет единственное решение — нулевое.

Если матрица СЛАУ не является квадратной невырожденной, то формулы Крамера не работают и приходится использовать другие методы нахождения решений.

Однородные системы

Теорема. Если столбцы ( X^, X^, ldots , X^ ) — решения однородной СЛАУ (AX=0), то любая их линейная комбинация также является решением этой системы.

Следствие. Если однородная СЛАУ имеет ненулевое решение, то она имеет бесконечно много решений.

Естественно попытаться найти такие решения ( X^, ldots , X^ ) системы (AX=0), чтобы любое другое решение этой системы представлялось в виде их линейной комбинации и притом единственным образом. Оказывается, что это всегда возможно и приводит к следующему определению.

Определение. Любой набор из (k=n-r) линейно независимых столбцов, являющихся решениями однородной СЛАУ (AX=0), где (n) — количество неизвестных в системе, а (r) — ранг её матрицы (A), называют фундаментальной системой решений этой однородной СЛАУ.

При исследовании и решении однородных систем линейных алгебраических уравнений будем использовать следующую терминологию. Если в матрице (A) однородной СЛАУ (AX=0) фиксировать базисный минор, то ему соответствуют базисные столбцы и, следовательно, набор неизвестных, отвечающих этим столбцам. Указанные неизвестные называют базисными, или зависимыми, а остальные неизвестные — свободными, или независимыми.

Теорема. Пусть дана однородная СЛАУ (AX=0) с (n) неизвестными и ( textA = r ). Тогда существует набор из (k=n-r) решений ( X^, ldots , X^ ) этой СЛАУ, образующих фундаментальную систему решений.

Если в фундаментальной системе решений все значения независимых неизвестных равны нулю, кроме одного, которое равно единице, то такую систему решений называют фундаментальной нормальной системой решений.

Следствие. С помощью нормальной фундаментальной системы решений однородной СЛАУ множество всех решений можно описать формулой :
$$ X = c_1X^ + ldots + c_kX^ $$
где постоянные ( c_i ;, quad i=overline ), принимают произвольные значения.

Следствие. Для существования ненулевого решения у однородной квадратной СЛАУ необходимо и достаточно, чтобы её матрица была вырождена.

Неоднородные системы

Рассмотрим произвольную СЛАУ (AX=B). Заменив столбец (B) свободных членов нулевым, получим однородную СЛАУ (AX=0), соответствующую неоднородной СЛАУ (AX=B). Справедливо следующее утверждение о структуре произвольного решения неоднородной СЛАУ.

Теорема. Пусть столбец (X^circ) — некоторое решение СЛАУ (AX=B). Произвольный столбец (X) является решением этой СЛАУ тогда и только тогда, когда он имеет представление (X = X^circ + Y ), где (Y) — решение соответствующей однородной СЛАУ (AY=0).

Следствие. Пусть (X’) и (X») — решения неоднородной системы (AX=B). Тогда их разность ( Y = X’ — X» ) является решением соответствующей однородной системы (AY=0).

Эта теорема сводит проблему решения СЛАУ к случаю однородной системы: чтобы описать все решения неоднородной СЛАУ, достаточно энать одно её решение (частное решение) и все решения соответствующей однородной СЛАУ.

Чтобы решить неоднородную систему, надо, во-первых, убедиться, что она совместна (например, по теореме Кронекера-Капелли), а во-вторых, найти частное решение (X^circ) этой системы, чтобы свести её к однородной системе.

Теорема о структуре общего решения СЛАУ. Пусть (X^circ) — частное решение СЛАУ (AX=B) и известна фундаментальная система решений ( X^, ldots , X^ ) соответствующей однородной системы (AX=0). Тогда любое решение СЛАУ (AX=B) можно представить в виде $$ X = X^circ + c_1 X^ + c_2 X^ + ldots + c_k X^ $$
где ( c_i in mathbb ;, quad i=overline ).
Эту формулу называют общим решением СЛАУ.

Видео:Решение системы уравнений методом ГауссаСкачать

Тест по дисциплине «Линейная алгебра» для ДПО ОСЭК

Вопрос 1

Линейную систему, у которой среди свободных членов имеются отличные от нуля, называют:

Вопрос 2

Вопрос 3

Вопрос 4

Вопрос 5

Выберите правильную формулировку теоремы Кронекера-Капелли:

Вопрос 6

Если ранг основной системы матрицы совместной системы равен числу неизвестных, то

Вопрос 7

Вопрос 8

Вопрос 9

Вопрос 10

Вопрос 11

Вопрос 12

Линейную систему, у которой все свободные члены равны нулю, называют:

Вопрос 13

Вопрос 14

Вопрос 15

Вопрос 18

Вопрос 19

Вопрос 20

Вопрос 21

Вопрос 22

Вопрос 23

Вопрос 24

Вопрос 25

Если любое решение одной системы является также решением другой системы и обратно, то такие две системы называют:

Вопрос 26

Если система имеет единственное решение, то ее называют:

Вопрос 27

Если система имеет хотя бы одно решение, то ее называют:

Вопрос 28

Если система не имеет ни одного решения, то ее называют:

Вопрос 29

Прибавление к одному уравнению системы другого уравнения, умноженного на любое число, называют:

Вопрос 30

Какое из ниже перечисленных преобразований не является элементарным?

Оставить комментарий

Inna Petrova 18 минут назад

Нужно пройти преддипломную практику у нескольких предметов написать введение и отчет по практике так де сдать 4 экзамена после практики

Иван, помощь с обучением 25 минут назад

Inna Petrova, здравствуйте! Мы можем Вам помочь. Прошу Вас прислать всю необходимую информацию на почту и написать что необходимо выполнить. Я посмотрю описание к заданиям и напишу Вам стоимость и срок выполнения. Информацию нужно прислать на почту info@the-distance.ru

Коля 2 часа назад

Здравствуйте, сколько будет стоить данная работа и как заказать?

Иван, помощь с обучением 2 часа назад

Николай, здравствуйте! Мы можем Вам помочь. Прошу Вас прислать всю необходимую информацию на почту и написать что необходимо выполнить. Я посмотрю описание к заданиям и напишу Вам стоимость и срок выполнения. Информацию нужно прислать на почту info@the-distance.ru

Инкогнито 5 часов назад

Сделать презентацию и защитную речь к дипломной работе по теме: Источники права социального обеспечения. Сам диплом готов, пришлю его Вам по запросу!

Иван, помощь с обучением 6 часов назад

Здравствуйте! Мы можем Вам помочь. Прошу Вас прислать всю необходимую информацию на почту и написать что необходимо выполнить. Я посмотрю описание к заданиям и напишу Вам стоимость и срок выполнения. Информацию нужно прислать на почту info@the-distance.ru

Василий 12 часов назад

Здравствуйте. ищу экзаменационные билеты с ответами для прохождения вступительного теста по теме Общая социальная психология на магистратуру в Московский институт психоанализа.

Иван, помощь с обучением 12 часов назад

Василий, здравствуйте! Мы можем Вам помочь. Прошу Вас прислать всю необходимую информацию на почту и написать что необходимо выполнить. Я посмотрю описание к заданиям и напишу Вам стоимость и срок выполнения. Информацию нужно прислать на почту info@the-distance.ru

Анна Михайловна 1 день назад

Нужно закрыть предмет «Микроэкономика» за сколько времени и за какую цену сделаете?

Иван, помощь с обучением 1 день назад

Анна Михайловна, здравствуйте! Мы можем Вам помочь. Прошу Вас прислать всю необходимую информацию на почту и написать что необходимо выполнить. Я посмотрю описание к заданиям и напишу Вам стоимость и срок выполнения. Информацию нужно прислать на почту info@the-distance.ru

Сергей 1 день назад

Здравствуйте. Нужен отчёт о прохождении практики, специальность Государственное и муниципальное управление. Планирую пройти практику в школе там, где работаю.

Иван, помощь с обучением 1 день назад

Сергей, здравствуйте! Мы можем Вам помочь. Прошу Вас прислать всю необходимую информацию на почту и написать что необходимо выполнить. Я посмотрю описание к заданиям и напишу Вам стоимость и срок выполнения. Информацию нужно прислать на почту info@the-distance.ru

Инна 1 день назад

Добрый день! Учусь на 2 курсе по специальности земельно-имущественные отношения. Нужен отчет по учебной практике. Подскажите, пожалуйста, стоимость и сроки выполнения?

Иван, помощь с обучением 1 день назад

Инна, здравствуйте! Мы можем Вам помочь. Прошу Вас прислать всю необходимую информацию на почту и написать что необходимо выполнить. Я посмотрю описание к заданиям и напишу Вам стоимость и срок выполнения. Информацию нужно прислать на почту info@the-distance.ru

Студент 2 дня назад

Здравствуйте, у меня сегодня начинается сессия, нужно будет ответить на вопросы по русскому и математике за определенное время онлайн. Сможете помочь? И сколько это будет стоить? Колледж КЭСИ, первый курс.

Иван, помощь с обучением 2 дня назад

Здравствуйте! Мы можем Вам помочь. Прошу Вас прислать всю необходимую информацию на почту и написать что необходимо выполнить. Я посмотрю описание к заданиям и напишу Вам стоимость и срок выполнения. Информацию нужно прислать на почту info@the-distance.ru

Ольга 2 дня назад

Требуется сделать практические задания по математике 40.02.01 Право и организация социального обеспечения семестр 2

Иван, помощь с обучением 2 дня назад

Ольга, здравствуйте! Мы можем Вам помочь. Прошу Вас прислать всю необходимую информацию на почту и написать что необходимо выполнить. Я посмотрю описание к заданиям и напишу Вам стоимость и срок выполнения. Информацию нужно прислать на почту info@the-distance.ru

Вика 3 дня назад

сдача сессии по следующим предметам: Этика деловых отношений — Калашников В.Г. Управление соц. развитием организации- Пересада А. В. Документационное обеспечение управления — Рафикова В.М. Управление производительностью труда- Фаизова Э. Ф. Кадровый аудит- Рафикова В. М. Персональный брендинг — Фаизова Э. Ф. Эргономика труда- Калашников В. Г.

Иван, помощь с обучением 3 дня назад

Вика, здравствуйте! Мы можем Вам помочь. Прошу Вас прислать всю необходимую информацию на почту и написать что необходимо выполнить. Я посмотрю описание к заданиям и напишу Вам стоимость и срок выполнения. Информацию нужно прислать на почту info@the-distance.ru

Игорь Валерьевич 3 дня назад

здравствуйте. помогите пройти итоговый тест по теме Обновление содержания образования: изменения организации и осуществления образовательной деятельности в соответствии с ФГОС НОО

Иван, помощь с обучением 3 дня назад

Игорь Валерьевич, здравствуйте! Мы можем Вам помочь. Прошу Вас прислать всю необходимую информацию на почту и написать что необходимо выполнить. Я посмотрю описание к заданиям и напишу Вам стоимость и срок выполнения. Информацию нужно прислать на почту info@the-distance.ru

Вадим 4 дня назад

Пройти 7 тестов в личном кабинете. Сооружения и эксплуатация газонефтипровод и хранилищ

Иван, помощь с обучением 4 дня назад

Вадим, здравствуйте! Мы можем Вам помочь. Прошу Вас прислать всю необходимую информацию на почту и написать что необходимо выполнить. Я посмотрю описание к заданиям и напишу Вам стоимость и срок выполнения. Информацию нужно прислать на почту info@the-distance.ru

Кирилл 4 дня назад

Здравствуйте! Нашел у вас на сайте задачу, какая мне необходима, можно узнать стоимость?

Иван, помощь с обучением 4 дня назад

Кирилл, здравствуйте! Мы можем Вам помочь. Прошу Вас прислать всю необходимую информацию на почту и написать что необходимо выполнить. Я посмотрю описание к заданиям и напишу Вам стоимость и срок выполнения. Информацию нужно прислать на почту info@the-distance.ru

Oleg 4 дня назад

Требуется пройти задания первый семестр Специальность: 10.02.01 Организация и технология защиты информации. Химия сдана, история тоже. Сколько это будет стоить в комплексе и попредметно и сколько на это понадобится времени?

Иван, помощь с обучением 4 дня назад

Oleg, здравствуйте! Мы можем Вам помочь. Прошу Вас прислать всю необходимую информацию на почту и написать что необходимо выполнить. Я посмотрю описание к заданиям и напишу Вам стоимость и срок выполнения. Информацию нужно прислать на почту info@the-distance.ru

Валерия 5 дней назад

ЗДРАВСТВУЙТЕ. СКАЖИТЕ МОЖЕТЕ ЛИ ВЫ ПОМОЧЬ С ВЫПОЛНЕНИЕМ практики и ВКР по банку ВТБ. ответьте пожалуйста если можно побыстрее , а то просто уже вся на нервяке из-за этой учебы. и сколько это будет стоить?

Иван, помощь с обучением 5 дней назад

Валерия, здравствуйте! Мы можем Вам помочь. Прошу Вас прислать всю необходимую информацию на почту и написать что необходимо выполнить. Я посмотрю описание к заданиям и напишу Вам стоимость и срок выполнения. Информацию нужно прислать на почту info@the-distance.ru

Инкогнито 5 дней назад

Здравствуйте. Нужны ответы на вопросы для экзамена. Направление — Пожарная безопасность.

Иван, помощь с обучением 5 дней назад

Здравствуйте! Мы можем Вам помочь. Прошу Вас прислать всю необходимую информацию на почту и написать что необходимо выполнить. Я посмотрю описание к заданиям и напишу Вам стоимость и срок выполнения. Информацию нужно прислать на почту info@the-distance.ru

Иван неделю назад

Защита дипломной дистанционно, «Синергия», Направленность (профиль) Информационные системы и технологии, Бакалавр, тема: «Автоматизация приема и анализа заявок технической поддержки

Иван, помощь с обучением неделю назад

Иван, здравствуйте! Мы можем Вам помочь. Прошу Вас прислать всю необходимую информацию на почту и написать что необходимо выполнить. Я посмотрю описание к заданиям и напишу Вам стоимость и срок выполнения. Информацию нужно прислать на почту info@the-distance.ru

Дарья неделю назад

Необходимо написать дипломную работу на тему: «Разработка проекта внедрения CRM-системы. + презентацию (слайды) для предзащиты ВКР. Презентация должна быть в формате PDF или формате файлов PowerPoint! Институт ТГУ Росдистант. Предыдущий исполнитель написал ВКР, но работа не прошла по антиплагиату. Предыдущий исполнитель пропал и не отвечает. Есть его работа, которую нужно исправить, либо переписать с нуля.

📺 Видео

Общее, частное, базисное решение системы линейных уравнений Метод ГауссаСкачать

Лекция 13. Исследование систем линейных уравнений. Теорема Кронекера — Капелли.Скачать

15. Однородная система линейных уравнений / фундаментальная система решенийСкачать

Метод Крамера за 3 минуты. Решение системы линейных уравнений - bezbotvyСкачать

Базисные решения систем линейных уравнений (03)Скачать

Математика без Ху!ни. Метод Гаусса.Скачать

12. Метод Гаусса решения систем линейных уравнений. Часть 1.Скачать

14. Метод Гаусса решения систем линейных уравнений ( бесконечное множество решений ). Часть 3Скачать

Неоднородная система линейных уравненийСкачать

13 Исследование систем линейных уравненийСкачать

Решение системы линейных уравнений методом ГауссаСкачать

Линейная алгебра, 6 урок, Ранг матрицыСкачать

Лекция 12. Системы линейных уравненийСкачать

Математика Без Ху!ни. Система линейных уравнений. Метод Крамера.Скачать