Одно из направлений функционально-графического метода решения уравнений связано с использованием возрастания и убывания функций, отвечающих частям уравнения. В этой статье мы подробно разберем соответствующий метод решения уравнений. Сначала скажем, для решения каких уравнений он предназначен, в чем он состоит, на чем базируется, и приведем его обоснование. Далее запишем алгоритм метода и дадим рекомендации к проведению его шагов. Наконец, рассмотрим решения характерных примеров.
- Какие уравнения решаются через возрастание/убывание?
- В чем состоит метод и на чем он базируется
- Обоснование метода
- Алгоритмы метода
- Рекомендации к определению корня
- Рекомендации к обоснованию возрастания/убывания функций
- Решение примеров
- Решение уравнений с помощью монотонности функций
- 2 комментария
- Применение монотонности функций для решения уравнений, неравенств и их систем
- Теорема о корне при решении уравнений. Урок алгебры. 9-й класс
- 🎥 Видео
Видео:Свойства функции. Промежутки возрастания и убывания функции. 10 класс.Скачать

Какие уравнения решаются через возрастание/убывание?
Для начала следует разобраться, какие уравнения могут быть решены посредством использования возрастания/убывания функций, отвечающих частям уравнения.
Во-первых, это уравнения f(x)=C , где f(x) – некоторое выражение с переменной x , а C – некоторое число, причем эти уравнения должны удовлетворять следующим критериям:
- Не видно альтернативных более простых методов решения уравнения.
- ОДЗ для уравнения есть некоторый числовой промежуток (позже в этом пункте мы скажем и про уравнения, ОДЗ для которых есть не отдельный числовой промежуток, а объединение нескольких промежутков).
- Есть возможность определить корень уравнения каким-либо способом, часто путем подбора.
- Есть возможность доказать возрастание или убывание функции f .
В качестве примера приведем уравнение 



Во-вторых, через возрастание/убывание решаются уравнения f(x)=g(x) , где f(x) и g(x) – это некоторые выражения с переменной x , удовлетворяющие следующим критериям:
- Не видно других более простых методов решения.
- ОДЗ для уравнения есть отдельный числовой промежуток (про уравнения, ОДЗ для которых есть объединение нескольких числовых промежутков, скажем чуть позже).
- Есть возможность определить корень уравнения.
- Есть возможность доказать возрастание одной из функций f или g и убывание другой.
Поясним на примере. Для этого подойдет уравнение 



Теперь про уравнения f(x)=C и f(x)=g(x) , ОДЗ для которых есть объединение нескольких числовых промежутков. Если они на отдельно взятом промежутке области допустимых значений удовлетворяют записанным выше критериям, то на этом промежутке можно получить их решение посредством использования возрастания/убывания. Если это сделать на каждом промежутке области допустимых значений, то будет получено решение уравнения в целом.
И вновь обратимся к конкретному примеру. Рассмотрим уравнение 
То есть, решение уравнений f(x)=C и f(x)=g(x) , ОДЗ для которых есть объединение нескольких числовых промежутков, сводится к решению этих уравнений на отдельно взятых промежутках. По этой причине метод решения можно постигать на уравнениях f(x)=C и f(x)=g(x) , ОДЗ для которых представляет отдельный числовой промежуток.
Видео:Как доказать, что функция убывает или возрастаетСкачать

В чем состоит метод и на чем он базируется
Метод состоит в нахождении корней решаемого уравнения любым доступным способом, часто подбором, и использовании возрастания/убывания для доказательства того, что других корней нет.
В основе метода лежат два следующих утверждения:
Если функция y=f(x) определена и возрастает или убывает на некотором промежутке X , и уравнение f(x)=C , где C – некоторое число, имеет корень на X , то этот корень единственный на X .
Если функции y=f(x) и y=g(x) определены на некотором промежутке X , причем одна из них убывает на этом промежутке, а другая – возрастает, и если уравнение f(x)=g(x) имеет на X корень, то этот корень единственный на X .
Видео:7 класс. Алгебра. Линейная функция. Возрастающая и убывающая. Коэффициент k.Скачать

Обоснование метода
Начнем с доказательства первого утверждения.
Пусть функция y=f(x) определена и возрастает или убывает на промежутке X , и пусть x0 – корень уравнения f(x)=C , где C – некоторое число, причем x0∈X . Докажем, что x0 – единственный корень уравнения f(x)=C на промежутке X .
Предположим, что уравнение имеет еще один корень на X , отличный от x0 , обозначим его x1 . Так как x0 и x1 — корни уравнения f(x)=C , то числовые равенства f(x0)=C и f(x1)=C – верные. Осуществив почленное вычитание этих числовых равенств, получим верное числовое равенство f(x0)−f(x1)=0 (см. свойства числовых равенств), откуда f(x0)=f(x1) . Но последнее равенство невозможно, так как функция f возрастающая или убывающая на X . Так методом от противного доказано, что x0 – единственный корень.
Теперь докажем второе утверждение.
Пусть функции y=f(x) и y=g(x) определены на промежутке X , одна из них возрастает, пусть это будет функция f , а другая функция g – убывает, и пусть уравнение f(x)=g(x) имеет на X корень x0 . Докажем, что x0 – единственный корень указанного уравнения на X . (Можно считать, что f – убывающая функция, а g – возрастающая, доказательство при этом аналогично).
Предположим, что уравнение f(x)=g(x) имеет еще один корень на X , отличный от x0 , обозначим его x1 . Так как корни x0 и x1 – корни уравнения f(x)=g(x) , то f(x0)=g(x0) и f(x1)=g(x1) — верные числовые равенства. Так как корни x0 и x1 различные, то либо x0 , либо x0>x1 . Разберем эти случаи по очереди.
Пусть x0 . При этом, так как функция f — возрастающая, то f(x0) , откуда f(x1)>f(x0) , а так как функция g – убывающая, то g(x0)>g(x1) . Из неравенства f(x1)>f(x0) и равенства f(x0)=g(x0) следует, что f(x1)>g(x0) , а из этого неравенства и неравенства g(x0)>g(x1) в силу свойства транзитивности (см. свойства числовых неравенств) следует, что f(x1)>g(x1) . Полученное неравенство означает, что x1 не является корнем уравнения f(x)=g(x) , что противоречит нашему предположению.
Пусть x0>x1 . При этом, так как функция f — возрастающая, то f(x0)>f(x1 ), откуда f(x1) , а так как функция g – убывающая, то g(x0) . Из неравенства f(x1) и равенства f(x0)=g(x0) следует, что f(x1) , а из этого неравенства и неравенства g(x0) в силу свойства транзитивности следует, что f(x1) . Полученное неравенство означает, что x1 не является корнем уравнения f(x)=g(x) , опять получили противоречие нашему предположению.
Так методом от противного доказано второе утверждение из предыдущего пункта.
Видео:Решение тригонометрических уравнений. Подготовка к ЕГЭ | Математика TutorOnlineСкачать

Алгоритмы метода
Сначала запишем алгоритмы решения уравнений f(x)=C и f(x)=g(x) , ОДЗ для которых есть числовой промежуток. После этого запишем алгоритм для случаев, когда ОДЗ представляет собой объединение нескольких числовых промежутков. Разъяснения к проведению шагов будут даны в следующих пунктах этой статьи.
Алгоритм решения уравнения f(x)=C , для которого ОДЗ есть числовой промежуток, посредством использования возрастания/убывания:
- Находим ОДЗ, убеждаемся, что она представляет собой некоторый числовой промежуток.
- Определяем корень уравнения любым доступным способом.
- Доказываем возрастание или убывание функции f . Это позволит утверждать, что найденный на предыдущем шаге корень является единственным корнем решаемого уравнения.
Алгоритм решения уравнения f(x)=g(x) , для которого ОДЗ есть числовой промежуток, через использование возрастания/убывания:
- Определяем ОДЗ, убеждаемся, что она представляет собой некоторый числовой промежуток.
- Определяем корень уравнения любым доступным способом.
- Доказываем возрастание одной из функций, отвечающих частям решаемого уравнения, и убывание другой. После этого можно делать вывод, что найденный на предыдущем шаге корень является единственным.
Для решения уравнений f(x)=C и f(x)=g(x) , ОДЗ для которых есть объединение нескольких числовых промежутков, посредством использования возрастания/убывания, надо проделать шаги, аналогичные шагам записанных алгоритмов, но на каждом отдельно взятом промежутке, составляющем ОДЗ, после чего взять объединение всех найденных корней.
То есть, для решения уравнения f(x)=C через возрастание/убывание, надо
- Определить ОДЗ.
- На каждом промежутке, составляющем ОДЗ, определить корень любым доступным способом.
- На каждом промежутке доказать убывание или возрастание функции f .
- Взять объединение корней, найденных на втором шаге. Это и есть искомое решение.
А для решения уравнения f(x)=g(x) через возрастание/убывание, надо
- Определить ОДЗ.
- На каждом промежутке, составляющем ОДЗ, определить корень любым доступным способом.
- На каждом промежутке доказать убывание одной из функций f или g , и возрастание другой функции.
- Взять объединение корней, найденных на втором шаге. Это и есть искомое решение.
Видео:Я теряю корни ★ 99 ошиблись ★ Решите уравнение ★ x^x=(1/2)^(1/2)Скачать

Рекомендации к определению корня
Корень характерных уравнений, которые решаются посредством использования возрастания/убывания, либо очевиден, либо довольно легко находится подбором. Дадим рекомендации, которые обычно позволяют справиться с подбором корня.
Первая рекомендация касается случаев, когда ОДЗ для уравнения представляет собой числовой отрезок, числовой полуинтервал или числовой интервал, содержащий некоторое небольшое количество целых чисел. В этих случаях корнем уравнения часто бывает одно из целых чисел области допустимых значений или одна из границ ОДЗ. Приведем пример.
В качестве примера возьмем уравнение 
Переходим ко второй рекомендации по подбору корня. Корнем уравнения часто служит число, при котором находятся точные значения составляющих это уравнение выражений (корней, степеней, логарифмов, тригонометрических функций и т.д.). Примеры возьмем из первого пункта текущей статьи.
Взглянем на первое уравнение 


Теперь взглянем на второе уравнение 


Еще мы приводили в пример уравнение 
Две приведенные рекомендации позволяют подобрать корень уравнения в подавляющем большинстве случаев, когда этого вообще возможно сделать без обладания сверхспособностями.
Видео:Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Рекомендации к обоснованию возрастания/убывания функций
Одним из путей доказательства возрастания или убывания функции является обращение к производной (см. нахождение промежутков возрастания/убывания функции). Например, через производную можно доказать, что на ОДЗ для уравнения 
Однако иногда можно обойтись без обращения к производной. Разберемся когда.
В первую очередь, не обязательно обращаться к производной для доказательства возрастания/убывания, когда мы имеем дело с хорошо изученными функциями, в частности, основными элементарными. Например, нам совсем не обязательно доказывать возрастание функции y=x 7 на промежутке (−7, 1) через производную, мы и так прекрасно знаем, что эта степенная функция возрастает на всей области определения, значит, она возрастает и на указанном промежутке.
Также для обоснования возрастания/убывания удобно привлекать свойства возрастающих и убывающих функций. Перечислим основные свойства, имеющие непосредственное отношение к нашей теме:
- Если функция y=f(x) возрастает (убывает) на некотором числовом промежутке X , то функция y=f(x)+C , где C – некоторое число, тоже возрастает (убывает) на X . Приведем пример использования записанного свойства. Допустим, нас интересует, как ведет себя функция y=arccosx−4 на интервале (−0,5, 0,1) . Мы знаем, что функция y=arccosx убывает на всей области своего определения [−1, 1] , значит, она убывает и на интервале (−0,5, 0,1) . Тогда, оперевшись на записанное свойство, мы можем утверждать, что функция y=arccosx−4 тоже убывает на (−0,5, 0,1) .
- Если функция y=f(x) возрастает на числовом промежутке X , то функция y=k·f(x) при k>0 возрастает на X , а при k убывает на X . Если функция y=f(x) убывает на числовом промежутке X , то функция y=k·f(x) при k>0 убывает на X , а при k возрастает на X . Приведем пример. Допустим, столкнувшись с задачей решить некоторое уравнение, мы пришли к выводу, что оно может быть решено посредством использования возрастания/убывания. Нашли ОДЗ для этого уравнения, ею оказался промежуток [0, +∞) . Подобрали корень – число 9 . Доказали, что функция, отвечающая левой части уравнения возрастает на множестве [0, +∞) . И осталось доказать, что функция
, отвечающая правой части уравнения, убывает на [0, +∞) . Как это сделать с использованием записанного свойства? Очень просто. Мы знаем, что функция
— возрастает на [0, +∞) . Значит, в силу записанного свойства, функция
убывает на [0, +∞) .
- Следствие. Если функция y=f(x) возрастает (убывает) на X , то функция y=−f(x) убывает (возрастает) на X . Например, степенная функция
убывает на промежутке (0, +∞) , значит, функция
возрастает на этом промежутке (0, +∞) .
- Следствие. Если функция y=f(x) возрастает (убывает) на X , то функция y=−f(x) убывает (возрастает) на X . Например, степенная функция
- Если функции y=f1(x) и y=f2(x) возрастающие (убывающие) на промежутке X , то функция y=f1(x)+f2(x) – возрастающая (убывающая) на X . Это свойство естественным образом распространяется на три и большее количество функций. Для удобства запоминания условно можно считать, что сумма возрастающих функций есть возрастающая функция, а сумма убывающих – убывающая функция. Например, функция y=x+x 3 +x 7 – возрастающая на множестве R , так как каждая из функций y=x , y=x 3 , y=x 7 возрастает на R . Другой пример:
— убывающая на промежутке (0, +∞) как сумма убывающей показательной функции
и убывающей логарифмической функции
.
- Следующее свойство относится к сложным функциям. Приведем его условную формулировку, так как она хорошо запоминается из-за схожести с правилами умножения чисел с разными знаками. Возрастающая от возрастающей и убывающая от убывающей есть функция возрастающая, а возрастающая от убывающей и убывающая от возрастающей есть функция убывающая. Здесь придется привести несколько примеров. Для начала рассмотрим функцию
и определим ее поведение на промежутке [3, 9] . Мы имеем дело со сложной функцией. Внутренняя функция – это логарифмическая функция
, внешняя функция – это степенная функция
. Так как основание логарифмической функции меньше единицы, то она убывает на всей своей области определения. Так как показатель степенной функции равен −1/2 , то функция убывает на своей области определения. Тогда функция
возрастает на своей области определения как убывающая от убывающей. В частности, она возрастает на интересующем нас промежутке [3, 9] . Другой пример. Как ведет себя функция
? Убывает как возрастающая от возрастающей от убывающей.
- Следствие. Если функция y=f(x) возрастает (убывает) на некотором числовом промежутке X и не обращается на нем в нуль, то функция y=1/f(x) убывает (возрастает) на X . Например, функция y=1/arcctgx – возрастает на всей области определения, так как функция y=arcctgx на своей области определения убывает и не обращается в нуль.
Умелое использование перечисленных свойств в соответствующих случаях дает возможность чуть ли не с одного взгляда на функцию определять ее возрастание или убывание.
Наконец, иногда для обоснования возрастания или убывания функции удобно использовать не производную, а определение возрастающей и убывающей функции в купе со свойствами верных числовых неравенств. Для примера обоснуем, что функция 












Видео:№17: монотонность в одном из сложнейших заданий ЕГЭ по математике 2022Скачать

Решение примеров
На страницах школьных учебников алгебры, начиная с 9 класса, встречается немало уравнений, решенных посредством обращения к возрастанию/убыванию соответствующих функций. В 9 классе изучаются степенные функции с натуральным показателем, после чего, естественно, показывается применение степенных функций и их свойств к решению уравнений. В этом свете в учебнике Мордковича представлено решение уравнения x 5 =3−2·x сначала графическим методом, затем – методом, предполагающим использование возрастания/убывания, причем сначала приведено утверждение, на котором базируется метод, с доказательством [1, с.120-121]. С решением этого уравнения все просто: легко подбирается корень x=1 , очевидно возрастание степенной функции y=x 5 и убывание линейной функции y=3−2·x , откуда следует, что найденный корень является единственным.
В учебнике для 10 классов в рамках разговора про обратные тригонометрические функции приводится решение уравнения 

В 11 классе в арсенал учащихся добавляются степенные функции с дробным показателем и иррациональным показателем, показательные и логарифмические функции. Естественно, там же встречаются соответствующие уравнения, решение которых завязано на использовании свойств этих функций, например, 

Давайте покажем полное решение одного из уравнений, которые мы приводили в пример в первом пункте этой статьи.
Решите уравнение
Видео:Промежутки возрастания и убыванияСкачать

Решение уравнений с помощью монотонности функций
Решение уравнений с помощью монотонности функций позволяет быстро и просто найти корень уравнения (либо доказать, что уравнение корней не имеет).
Использование возрастания и убывания функций при решении уравнений опирается на следующие теоремы.
1) Если на некотором промежутке функция f(x) возрастает (или убывает), то уравнение f(x)=a на этом промежутке имеет единственный корень либо не имеет корней (a — постоянная величина (число)).
2) Если на некотором промежутке функция f(x) возрастает, а функция g(x) убывает (либо наоборот), то уравнение f(x)=g(x) на этом промежутке имеет единственный корень либо не имеет корней.
Доказав, что уравнение имеет на промежутке не более чем один корень, можно попытаться определить его подбором.
Если функция имеет несколько промежутков возрастания и убывания, каждый из них следует рассмотреть отдельно.
Сумма возрастающих функций — возрастающая функция. Сумма убывающих функций — убывающая функция.
Прибавление или вычитание постоянной величины не влияет на монотонность функции. Если к возрастающей функции прибавить (или вычесть) постоянную величину, получим возрастающую функцию. Если к убывающей функции прибавить (или вычесть) постоянную величину, получим убывающую функцию.
Таким образом, использование монотонности функций при решении уравнений схематически можно изобразить так:
то уравнение имеет единственный корень или не имеет корней.
Разумеется, количество слагаемых может быть больше двух.
Некоторые функции, возрастающие на всей области определения либо на каждом из промежутков, из объединения которых состоит область определения (k>0, b≥0, n — целое):
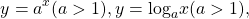
Некоторые функции, убывающие на всей области определения либо на каждом из промежутков, из объединения которых состоит область определения:
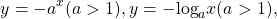
Примеры решения уравнений с помощью использования монотонности функций.
Перепишем уравнение в виде
является возрастающей (как сумма возрастающих функций). Следовательно, уравнение имеет не более одного корня. Подбором находим, что x=1.
На промежутке (-∞;0) функция
— убывает, следовательно, уравнение имеет не более одного корня. Подбором находим x= -1.
Аналогично, на промежутке (0:∞)
— убывает, следовательно, уравнение имеет не более одного корня. Подбором находим x=1.
В алгебре решение уравнений с применением возрастания и убывания функций чаше всего используется при решении иррациональных, логарифмических, показательных уравнений. Полезно взять на вооружение этот удобный и быстрый способ.
2 комментария
Добрый день. Вот это схематическое изображение монотонности очень интересно, но там не все понятно. Что вы подразумеваете под знаками равно и минус? И вот это: сумма убывающих_возрастающая? Буду благодарна комментариям
Елена, «=» — знак равенства между левой и правой частями уравнения.
Сумма убывающих функций — убывающая функция. Соответственно, одна часть уравнения — убывающая функция, а другая — возрастающая, то применима вторая теорема.
Аналогично, сумма возрастающих функций есть возрастающая функция. Если с одной стороны — возрастающая функция, с другой — убывающая, можем применить первую теорему.
Если к монотонно возрастающей функции прибавить число (или вычесть), то это никак не повлияет на её монотонность (это наглядно можно продемонстрировать графически: график функции y=f(x)±b получен из графика y=f(x) параллельным переносом на b единиц вверх или вниз вдоль оси Oy). Поэтому, если в одной части уравнения — монотонно возрастающая функция ± число, а в другой — монотонно убывающая функция, можем применить теорему два. И т.д.
Видео:Параметр. Серия 5. Что такое монотонная функция и как с ее помощью решать задачиСкачать

Применение монотонности функций для решения уравнений, неравенств и их систем
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Рабочие листы и материалы для учителей и воспитателей
Более 2 500 дидактических материалов для школьного и домашнего обучения
Столичный центр образовательных технологий г. Москва
Получите квалификацию учитель математики за 2 месяца
от 3 170 руб. 1900 руб.
Количество часов 300 ч. / 600 ч.
Успеть записаться со скидкой
Форма обучения дистанционная
311 лекций для учителей,
воспитателей и психологов
Получите свидетельство
о просмотре прямо сейчас!
Применение монотонности функций для решения уравнений, неравенств и их систем
Решение целого ряда нестандартных задач во многих случаях основано на некоторых свойствах функций. К таким свойствам относятся монотонность, периодичность, четность, нечетность, непрерывность и другие свойства.
Я остановлюсь на применении монотонности функции для решения уравнений, неравенств и их систем. Этому методу я уделяю достаточно большое внимание на уроках в 9-11 классах математической направленности, при подготовке к экзаменам и в индивидуальной работе с учениками при подготовке к олимпиадам. Отмечу, что непосредственно монотонности функций в программе 9 — 11 классов посвящено мало уроков, поэтому для закрепления и расширения теоретических знаний, а также для формирования практических навыков применения свойств монотонных функций при решении задач я использую любую возможность: при изучении рациональных, иррациональных, показательных, логарифмических и других уравнений, неравенств и их систем (в том числе и с параметрами).
В решении задач с использованием монотонности функции можно выделить два ключевых момента: во-первых, доказать, что некоторая функция (или функции) монотонна, и, во-вторых, применить соответствующую теорему о монотонной функции для решения данной задачи.
Для доказательства монотонности функции в старших классах часто используется производная (достаточный признак возрастания или убывания функции). Однако во многих случаях доказать монотонность можно с помощью элементарных методов. Перечислим некоторые утверждения о монотонности:
1) Если функция f возрастает на множестве Х, то для любого числа с функция f + с тоже возрастает на Х.
2) Если функция f возрастает на множестве Х и c > 0, то функция 
3) Если функция f возрастает и сохраняет знак на множестве Х, то функция 
4) Если функции f и g возрастают на множестве Х, то их сумма f + g тоже возрастает на Х.
5) Если функции f и g возрастают и неотрицательны на множестве Х, то их произведение 
6) Если функция f возрастает и неотрицательна на множестве Х и п – натуральное число, то функция 
7) Если функции f и g возрастающие (убывающие), то функция 

Следует обратить особое внимание на утверждения 3, 5 и 6, которые содержат дополнительные условия: функция неотрицательна или функция не меняет знак на множестве Х, так как при не выполнении этих условий указанные утверждения становятся, вообще говоря, неверными.
Утверждения, аналогичные утверждениям 1 — 6, можно сформулировать и для убывающих функций, а также можно получить ряд других утверждений.
Полезно также отметить, что если четная функция на множестве Х 
Рассмотрим несколько теорем о применении монотонности к решению уравнений.
Если на некотором промежутке функция 

Если на некотором промежутке одна из функций 


Пусть функция f ( x ) монотонна. Тогда для любых 



Пусть 


Следствие из теоремы 4:
Для любой возрастающей функции f ( x ) и любого натурального п уравнения
и 
Рассмотрим примеры решения некоторых задач разного уровня сложности.
1. Решить уравнение:
Подбором находим корень уравнения: х = 1. Докажем, что других корней нет. Так как функции 



2. Решить уравнение:
Легко видеть, что 1 – корень данного уравнения. Разделим обе части уравнения на 

3. Решить уравнение:
Так как функция 



4. Решить уравнение 
ОДЗ: 











5. Решить систему уравнений:
Рассмотрим первое уравнение системы. Пусть х + у = t , тогда получаем уравнение 








6. Решить неравенство 
Область определения данного неравенства задается условием 





Теперь решим уравнение 













Ответ : 
7. Решить уравнение:
Выполним равносильные преобразования данного уравнения:


Это уравнение имеет вид 










8. Решить уравнение:
Так как 



Это уравнение имеет вид 










Докажем монотонность функции 









Таким образом, функция 

9. При каких значениях параметра а уравнение


ОДЗ: 
Выполним равносильные преобразования заданного уравнения:


















Видео:Линейное уравнение с двумя переменными. 7 класс.Скачать

Теорема о корне при решении уравнений. Урок алгебры. 9-й класс
Разделы: Математика
Класс: 9
Цели урока:
- Использование особенностей монотонности функций для активизации творческого мышления учащихся.
- Формирование у школьников навыков применения теоремы о корне для решения уравнений.
- Умение обобщать, конкретизировать и анализировать изучаемый материал.
- Обучение учащихся нестандартным способам решения задач.
- Развитие логики и навыков самостоятельной работы.
- Воспитание ответственного отношения к учебному труду.
Тип урока: урок изучения нового материала.
Оборудование: учебник “Алгебра 9” (автор: Мордкович А. Г.), задачник “Алгебра 9” (авторы: Мордкович А. Г., Тульчинская Е.Е. и др.), книга для преподавателей “Алгебра 9” (авторы: Афанасьева Т.Л., Тапилина Л.А.), карточки с памяткой для самостоятельной работы по данной теме, компьютер, мультимедийный проектор, экран.
Предложенный урок расширяет программу по теме “Функции”. Учащиеся уже знакомы с основными свойствами функций, владеют навыками грамотного чтения графиков и умеют применять алгоритм исследования функций. На уроке основной упор делается на использование свойств монотонности функций для решения уравнений. Рассматривается теорема о корне. В ходе урока каждый учащийся должен достигнуть определенного уровня понимания материала, поэтому этап усвоения знаний разработан дифференцированно.
Ожидаемый результат по окончании изучения материала:
1-й уровень: каждый ученик должен знать геометрическую модель теоремы о корне и уметь установить связь монотонности функций, входящих в уравнение, с количеством корней соответствующего уравнения.
2-й уровень: каждый ученик должен знать алгоритм решения уравнений с использованием теоремы о корне и уметь применять ее для решения нестандартных задач.
На уроке рассматриваются различные виды уравнений, решаемых с помощью теоремы о корне. В дальнейшем учащимся предлагается использовать предложенный алгоритм в домашней контрольной работе (§16, задачник “Алгебра 9” авторы: Мордкович А. Г., Тульчинская Е.Е. и др.). Для организации проверочной работы используются задания из практикума (составитель автор).
Ход урока
I этап. Организационный момент (1 мин.).
II этап. Актуализация опорных знаний и умений (7 мин.).
Учитель: Необходимо повторить пройденное для того, чтобы успешно перейти к усвоению нового материала. На протяжении изучения темы “Функции” вы постепенно учились читать графики функций, используя алгоритм для их исследования. Остановимся на особенностях возрастающей и убывающей функций. Подборка материала подготовлена учащимися.
Выступление учащихся сопровождается показом презентации.
III этап. Объяснение нового материала (10 мин).
Учитель: Сегодня изучение нового материала мы начнем с доказательства теоремы о корне.
Теорема о корне.
Пусть функция y=f(x) возрастает (или убывает) на множестве 
Доказательство:
Рассмотрим возрастающую функцию f(x) (в случае убывающей функции рассуждения аналогичны). По условию на множестве X существует такое число b, что f(b)=a. Покажем, что b — единственный корень уравнения f(x)=a.
Допустим, что на множестве X есть еще число 
Геометрическая модель теоремы о корне может быть представлена как на экране, так и на плакате.
Учитель: Давайте вместе рассмотрим следующие примеры:
Сколько корней имеет уравнение?

— x 5 = 
Учащиеся отмечают, что на своих областях определения функция 
Учитель: Откроем учебник на 98 стр. и обратим внимание на то, что при решении уравнения x 5 =3-2x (пример 1, рис. 79) геометрическая модель наглядно иллюстрирует следствие, которое следует из теоремы о корне:
Следствие.
“Если функция y=f(x) возрастает, а функция y=g(x) убывает и если уравнение f(x)=g(x) имеет корень, то только один”.
По учебнику разбирается пример 1.
Опираясь на это утверждение, можем изящно решить уравнение
x 5 = 3 — 2x без чертежа, следуя следующему алгоритму:
- заметим, что при x=1 выполняется равенство 1 5 =3-2·1,
значит, x=1 – корень уравнения (этот корень мы угадали); - функция у = 3 — 2x убывает, а функция у = x 5 возрастает,
значит, корень у заданного уравнения только один и
этим корнем является значение x=1.
Учитель: Определим сколько решений имеет уравнение x 5 = — 3x +5 с комментированием на месте.
Решение:
- рассмотрим функции у = x 5 и у = — 3x + 5; заметим, что область определения этих функций одинакова: D(у)=(-
; +
);
- на D(у) функция у = — 3x + 5 убывает, а функция у = x 5 возрастает. Значит, по следствию из теоремы о корне, у заданного уравнения только один корень, т.е. уравнение, имеет одно решение.
Учитель: Цель нашего урока состоит в том, чтобы научиться решать задачи, используя теорему о корне (следствие).
На экране высвечивается обобщенный алгоритм решения уравнения f(x)=g(x) с использованием следствия из теоремы о корне:
- Определить при каких значениях x уравнение превращается в верное числовое равенство, (т.е. угадать корень уравнения – x=b).
- Ввести две функции y=f(x) и y=g(x).
- Исследовать y=f(x) и y=g(x) на монотонность. Если y=f(x)возрастает (убывает), а y=g(x) убывает (возрастает), то уравнение f(x)=g(x) имеет единственный корень – x=b (ссылка на следствие).
IV этап. Усвоение новых знаний (23 мин.)
Учитель: Карточки и памятка для самостоятельной работы лежат у вас на столах. Приступим к выполнению заданий.
Так как нетрадиционные методы решения задач вызывают трудность у большинства учащихся, то следующее уравнение предлагается решить вместе. Для оформления решения учащийся по желанию выходит к доске (дается уравнение 2 уровня).
Решить уравнение: 
Решение: в начале запишем уравнение (3) в виде

затем воспользуемся теоремой о корне.
- при x=5 уравнение превращается в верное числовое равенство:
; 5=5 (т.е. угадали корень уравнения – x=5).
- заметим, что в левой части уравнения функция
возрастает на D(у)=[3; +
); значит, у заданного уравнения корень только один и этим корнем является значение x=5.
После того как данное задание выполнено, класс приступает к решению уравнений в зависимости от восприятия материала:
1) те, кто попытается справиться самостоятельно с не очень сложными уравнениями;
2) те, у кого решение уравнений не вызывает затруднений.
В соответствии с этим учащиеся получают дифференцированные задания.
1 уровень.
1. 
2. 
3. 
4. 
5. 
6. 
2 уровень.
1. 
2. 
3. 
4. 
5. 
6. 
7. 
Необходимо проверить правильность выполнения заданий, поэтому от каждой группы выступает ученик, демонстрируя решение одного из уравнений на доске.
V этап. Итог урока (2 мин.).
Подводя итог урока, учитель и ученики выясняют трудности при решении уравнений и обсуждают, на что они должны обратить внимание при выполнении домашнего задания.
VI этап. Домашнее задание (1мин.).
Учитель: задание на дом следующее: доделать задания на карточках; если на уроке выполнено все, то воспользоваться дополнительной карточкой из материалов для самостоятельной работы; домашняя контрольная работа (§16, задачника “Алгебра 9”).
Заключительное слово учителя (1мин). Любовь к предмету не возникает просто так. Двигаясь постепенно от простого к сложному, анализируя и обобщая учебный материал, интересуясь “изящными” способами решения, можно понять красоту алгебры. Сегодня знание теории и практические навыки, что равнозначно, показали многие из вас. Особую благодарность заслуживают ребята, создавшие прекрасную презентацию. Постижение мира бесконечно: дерзайте, творите, ошибайтесь, ищите ответы на вопросы, только не “проспите” лучшие годы. “Жажда к жизни” – залог успеха.
Материалы к уроку для самостоятельной работы учащихся
1. Памятка по решению уравнений.
Теорема о корне.
Пусть функция y=f(x) возрастает (или убывает) на множестве 
Следствие.
“Если функция y=f(x) возрастает, а функция y=g(x) убывает и если уравнение f(x)=g(x) имеет корень, то только один”.
Алгоритм решения уравнения f(x)=a с использованием теоремы о корне:
- определить при каких значениях x уравнение превращается в верное числовое равенство, (т.е. угадать корень уравнения – x=b);
- исследовать функцию y=f(x), стоящую в левой части уравнения, на монотонность. Если y=f(x) возрастает (убывает), то уравнение f(x)=a имеет единственный корень – x=b (ссылка на теорему).
Алгоритм решения уравнения f(x)=g(x) с использованием следствия из теоремы о корне:
Рекомендации:
Сначала, если это необходимо, уравнение привести к такому виду, чтобы было удобно исследовать на монотонность функции, стоящие в левой и правой частях уравнения, а затем следовать согласно следующему алгоритму:
- определить при каких значениях x уравнение превращается в верное числовое равенство, (т.е. угадать корень уравнения – x=b);
- ввести две функции y=f(x) и y=g(x);
- исследовать y=f(x) и y=g(x) на монотонность. Если y=f(x) возрастает (убывает), а y=g(x) убывает (возрастает), то уравнение f(x)=g(x) имеет единственный корень – x=b (ссылка на следствие).
2. Практические задания.
Рекомендации: рассмотрим готовое решение уравнения (возможен такой вариант оформления).
Решить уравнение: 
Решение:
Функция f(x) = 

На основании теоремы о корне уравнение имеет не более одного корня.
Т.к. f (1) = 4, то x = 1 – корень уравнения.
Дополнительная карточка (подбор заданий [1]).






Литература.
- Ткачук В.В. Математика абитуриенту. – М.: МЦНМО, 2005.
🎥 Видео
✓ Параметры с нуля и до ЕГЭ | Задание 17. Профильный уровень | #ТрушинLive #041 | Борис ТрушинСкачать

Параметры, Легко Решаемые Графически | ЕГЭ 2024 по математикеСкачать

Уравнение с двойным модулем | Параметр 3 | mathus.ru |Скачать

Как решать уравнения с модулем или Математический торт с кремом (часть 1) | МатематикаСкачать

Решение простых уравнений. Что значит решить уравнение? Как проверить решение уравнения?Скачать

Задание 18 ЕГЭ по математике #14Скачать

Урок 7 ЛИНЕЙНОЕ УРАВНЕНИЕ С ОДНОЙ ПЕРЕМЕННОЙСкачать

Все уравнения с параметром на РешуЕГЭ. Тотальный разбор 17 номера ЕГЭ по математикеСкачать

Параметры 11 - монотонность - часть 2 практикаСкачать

Одно уравнение и два метода решения #shortsСкачать

 , отвечающая правой части уравнения, убывает на [0, +∞) . Как это сделать с использованием записанного свойства? Очень просто. Мы знаем, что функция
, отвечающая правой части уравнения, убывает на [0, +∞) . Как это сделать с использованием записанного свойства? Очень просто. Мы знаем, что функция  убывает на промежутке (0, +∞) , значит, функция
убывает на промежутке (0, +∞) , значит, функция  возрастает на этом промежутке (0, +∞) .
возрастает на этом промежутке (0, +∞) . — убывающая на промежутке (0, +∞) как сумма убывающей показательной функции
— убывающая на промежутке (0, +∞) как сумма убывающей показательной функции  и убывающей логарифмической функции
и убывающей логарифмической функции  .
. и определим ее поведение на промежутке [3, 9] . Мы имеем дело со сложной функцией. Внутренняя функция – это логарифмическая функция
и определим ее поведение на промежутке [3, 9] . Мы имеем дело со сложной функцией. Внутренняя функция – это логарифмическая функция  , внешняя функция – это степенная функция
, внешняя функция – это степенная функция  . Так как основание логарифмической функции меньше единицы, то она убывает на всей своей области определения. Так как показатель степенной функции равен −1/2 , то функция убывает на своей области определения. Тогда функция
. Так как основание логарифмической функции меньше единицы, то она убывает на всей своей области определения. Так как показатель степенной функции равен −1/2 , то функция убывает на своей области определения. Тогда функция  ? Убывает как возрастающая от возрастающей от убывающей.
? Убывает как возрастающая от возрастающей от убывающей.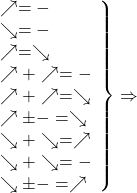
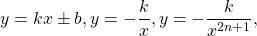
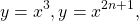
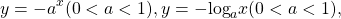
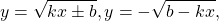
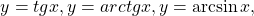
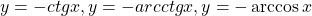
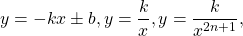
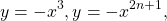
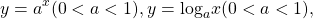
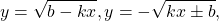
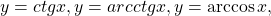
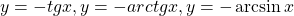
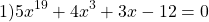
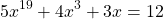
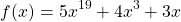
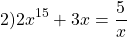
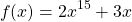








 ; +
; + ; 5=5 (т.е. угадали корень уравнения – x=5).
; 5=5 (т.е. угадали корень уравнения – x=5). возрастает на D(у)=[3; +
возрастает на D(у)=[3; +