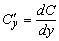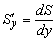Применение понятия производной
Пусть функция 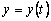
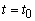
За период времени от t 0 до 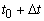

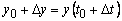
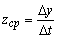
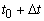
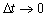

Следовательно , производительность труда есть скорость изменения количества произведенной продукции за единицу времени. Заметим, что вторая производная от количества произведенной продукции по времени является ускорением для данной функции, или скоростью для производительности труда за единицу времени.
Пример 1 . Объем продукции, произведенной бригадой рабочих за восьмичасовую смену, описывается уравнением 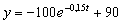
Решение . Производительность труда
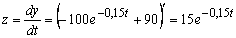
скорость ее изменения
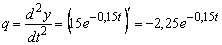
В начале рабочего дня (при t 0 =0) производительность труда бригады 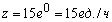
скорость ее изменения 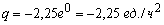
В конце рабочего дня (при 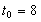
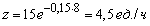
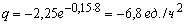
Пример 2 . Объем продукции, произведенной бригадой рабочих, может быть описан уравнением
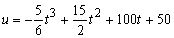
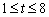
t — рабочее время в часах. Вычислить производительность труда, скорость и темп ее изменения через час после начала работы и за час до ее окончания.
Решение . Производительность труда
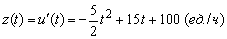
скорость изменения производительности
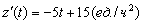
темп изменения производительности
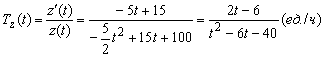
В момент времени 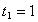
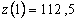
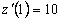
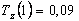
В момент времени 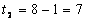
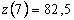
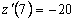
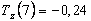
Итак, к концу работы производительность труда существенно снижается; при этом изменение знака 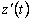
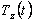
Издержки производства и прибыль
Издержки производства C однородной продукции есть функция количества выпускаемой продукции Q , т.е. 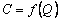
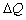
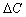
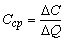
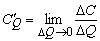
выражает предельные издержки производства и характеризует приближенно дополнительные затраты на производство единицы дополнительной продукции.
Предельные издержки зависят от количества выпускаемой продукции и определяются переменными производственными затратами на сырье, топливо и т.п.
Аналогично находятся предельная выручка (доход)
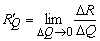
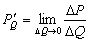
Кроме издержек производства товара, существуют издержки его хранения.
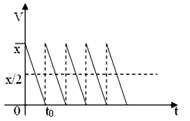
Пусть товар завозится на склад партиями по х штук в одной партии, а расходуется с постоянной скоростью. Тогда наполняемость склада зависит от времени t и задается функцией, график которой представлен на рис. 1.
На графике V — количество товара на складе, x /2 — средняя наполняемость склада, t 0 — время использования партии товара.
Издержки производства товара и издержки его хранения представляют собой совокупные издержки.
Заметим, что в экономической литературе предельные величины называют также маржинальными.
При их записи к обычному обозначению величин добавляется буква М; при записи средних величин добавляется буква А (от англ. Average — средняя). Например, MR — предельный доход, AR — средний доход.
Пример 3. Издержки производства С, зависящие от объема продукции Q , выражаются уравнением 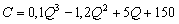
Решение. Предельные издержки определяются выражением 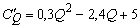
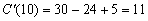
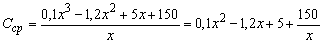
откуда 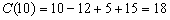
Сравнение значений средних и предельных издержек производства при выпуске 10 ед. продукции означает, что увеличение объема на 1 ед. продукции обойдется фирме приближенно в 11 ден. ед. при средних затратах на производство 1 ед. продукции 18 ден. ед.
Потребление и сбережение
Доход y , остающийся у населения после уплаты налогов, состоит из двух слагаемых: 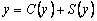
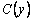
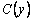
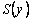
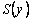
Если национальный доход Y получает приращение 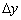
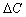
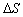
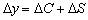
Разделив последнее равенство на ∆ y ≠ 0 , перейдем к пределу при 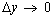
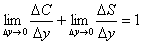
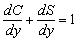
называется предельной склонностью к потреблению, производная
— предельная склонность к сбережению.
Заметим, что полученные предельные величины позволяют определить изменения потребления и сбережения при увеличении (уменьшении) национального дохода.
Пример 4. Зависимость потребления от национального дохода задается выражением 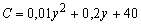
Решение . Предельная склонность к потреблению
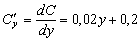
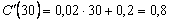
Предельную склонность к сбережению найдем, пользуясь равенством
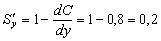
При данном уровне национального дохода население больше склонно проедать его. Если национальный доход увеличить на 1 ед. от уровня 30, то потребление вырастет на 0,8 и только 0,2 пойдут на инвестиции.
Производственная функция является экономико-математическим уравнением, связывающим переменные величины затрат (ресурсов) с величинами продукции (выпуска). Пусть количество продукции Q зависит только от приложенного труда L (численности персонала). Производственная функция примет вид 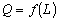
Для оценки эффективности производства используется средняя производительность труда PL , которая определяется отношением 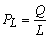
Руководителей больше интересуют изменения объема продукции Q при увеличении (уменьшении) численности персонала. Понятие предельной производительности труда как производной от продукции Q по величине приложенного труда L позволяет получить ответ, т.е. 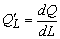
Предельная производительность приближенно равна изменению объема выпускаемой продукции при изменении численности персонала на единицу.
Пример 5. Производственная функция задана в виде
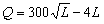
Решение . Предельная производительность труда
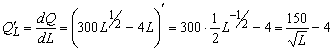
Подставим в полученную формулу значения L : 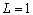
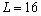
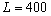
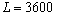
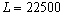
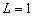
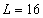
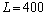
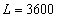
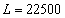
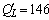
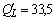
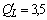
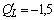
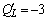
Из полученных результатов видно, что предельная производительность труда уменьшается с ростом численности персонала. Значит, при дальнейшем увеличении персонала производство продукции будет падать, так как исполнители одного и того же дела начинают мешать друг другу.
Видео:Кадры и производительность труда!Скачать

Деловая игра Занятие по теме: «Приложение производной в экономике»
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Рабочие листы и материалы для учителей и воспитателей
Более 2 500 дидактических материалов для школьного и домашнего обучения
«Приложение производной в экономике»
Показать применение исследования функции к решению прикладных задач и в ходе ее решения обобщить и систематизировать алгоритм исследования функций и построения графиков.
В процессе подготовки и выполнения заданий продолжать формировать чувство ответственности за результаты своей работы, самокритичности в оценке результатов решения задач наряду с чувством уверенности в правильности выполнения работы.
Основные знания и умения
Знать правила исследования функций и построения графиков. Уметь исследовать функции на возрастание и убывание, экстремум, наибольшее и наименьшее значение на отрезке, строить графики.
Раздаточный материал: карточки задания для групповой работы. Вычислительные средства: микрокалькуляторы.
Урок применения знаний и умений
Форма урока: дидактическая игра
Тема игры: исследование производительности труда
Последовательность хода занятия
1. Сообщить цели и задачи урока.
2. Выдать группам индивидуальное задание, на решение которого отводится 15 минут.
3. Группы готовят ответ-защиту своих решений, а в это время руководители групп составляют общий отчет.
4. Обсуждение решений и общего отчета.
5. Подведение итогов и выставление оценок.
1. Сообщение цели и задачи урока
Мы изучили тему «Производная», познакомились со способами исследования функции, рассмотрели физический, геометрический и экономический смысл производной. Цель сегодняшнего урока заключается в том, чтобы от производственной ситуации перейти к математической модели. Необходимо проанализировать, логически осмыслить, обобщить поставленную задачу и подготовить творческий отчет.
В процессе подготовки и выполнения заданий необходимо проявить чувство ответственности за результаты своей работы, самокритичность в оценке результатов решения задач наряду с чувством уверенности в правильности выполнения работы.
2. Сообщение условия игры
Вы являетесь сотрудниками НИИ. Институт получил заказ от одного из заводов города исследовать изменение производительности труда одной, отдельно взятой бригады в течение рабочего дня. Выполнить заказ поручили вашему отделу. Каждая группа отдела решает свою задачу. Итогом работы группы является отчет и его защита. Руководители групп вместе с начальником отдела готовят отчет — проект заказа для института.
По итогам конкурса на должность начальника отдела и руководителей групп назначены___________________________________________________________
Каждая группа получает индивидуальное задание и приступает к его выполнению. Руководители групп могут обращаться за помощью к начальнику отдела. На выполнение задания дается 15 минут. По истечении времени руководители групп и начальник отдела приступают к оформлению отчета.
В это время группы готовят защиту своих решений.
Через 10 минут мы приступаем к обсуждению результатов работы. При оценивании будут учитываться:
1) Время решения задачи.
2) Качество решения задачи.
3) Четкость и ясность защиты.
4) Сознательный и творческий подход к выводу.
5) Самостоятельность в работе.
Объем продукции u ( t ), произведенный бригадой рабочих, может быть описан уравнением u (t) = — 5/6 t 3 + 15/2 t 2 + 100 t + 50 (ед.), 1 ≤ t ≤ 8, где t — рабочее время в часах.
1) Найти производительность труда, исследовать ее и построить график изменения производительности труда. Сделать вывод.
2) Найти скорость изменения производительности труда. Исследовать ее и построить график. Вычислить скорость изменения производительности труда через час после начала работы и за час до ее окончания. Сделать вывод.
3) Найти темп изменения производительности труда. Вычислить темп изменения производительности труда через час после начала работы и за час до ее окончания. Сделать вывод.
4) Найти наибольший и наименьший объем выпущенной продукции. Вычислить производительность труда через час после начала работы и за час до ее окончания. Сделать вывод.
5) Вычислить наибольшее и наименьшее значения производительности труда и время, в которое она бывает. Сделать вывод.
Когда целесообразнее всего сделать перерыв? Ответ обосновать.
На решение задачи каждой группой, дается 15 минут. Через 15 минут, или раньше, руководители групп предоставляют решения начальнику отдела и совместно подводят итог работы, делая общий вывод.
3. Подготовка защиты решений и составление общего отчета
Группы готовят защиту решений, руководители групп составляют общий отчет.
4. Обсуждение решений и общего отчета
Каждой группе дается 5 минут для выступления и 10 минут выделяется для обсуждения общего отчета.
5. Подведение итогов и выставление оценок
Подсчитать общее количество баллов по каждой группе. Сообщить результат и дать время для того, чтобы учащиеся обсудили и самостоятельно выставили оценки каждому участнику игры.
По каждому критерию максимальная оценка 5 баллов, максимальная оценка группе – 20 баллов, максимальная оценка руководителям групп – 20 баллов.
При выставлении оценок учесть, что:
1) заказчик выставляет оценку начальнику отдела, главному консультанту и назначает общий балл руководителям групп;
2) руководителям групп выставляют оценку начальник отдела и главный консультант, причем пятерку могут получить только те начальники отделов, чьи группы набрали не менее 20 баллов, а сумма оценок руководителей групп не должна превышать общего балла, который назначил руководителям групп заказчик.
3) остальные сотрудники отдела получают оценку, исходя из общего количества баллов группы, так чтобы оценка каждого не превосходила оценки руководителя.
4) заказчик имеет право проверить объективность любой выставленной оценки.
ТАБЛИЦА ПОДВЕДЕНИЯ ИТОГОВ ПО ГРУППАМ
Видео:Производная: секретные методы решения. Готовимся к ЕГЭ | Математика TutorOnlineСкачать

Практикум по решению математических задач с экономическим содержанием по разделу «Дифференциальное исчисление»
ПРАКТИКУМ ПО РЕШЕНИЮ МАТЕМАТИЧЕСКИХ ЗАДАЧ
С ЭКОНОМИЧЕСКИМ СОДЕРЖАНИЕМ
по разделу «Дифференциальное исчисление»
Материалы для практикума
ТЕМА 1.Использование понятия производной для решения задач по экономической теории.
Пусть µ= µ(t)-обьем продукции, произведенной за время t, тогда относительное приращение

Производная µ


Задача. Зависимость объема произведенной рабочим продукции от времени t задается формулой µ(t)= 10- 

Найти производительность труда рабочего через 2 часа и через 10 часов после начала работы.
Решение. Из экономического смысла производной производительность равна
µ



µ



Задача 1. Объем продукции u (усл. ед.) цеха в течение рабочего дня представляет функцию u = — t? — 5t?+ 75t+ 425, где t — время (ч). Найти производительность труда через 2 часа после начала работы.
Задача 2. Зависимость объема между произведенной рабочим продукции от времени t задается формулой µ(t)= 15- 

Найти производительность труда рабочего через 3 часа и через 10 часов после начала работы.
Задача 3. Объем продукции u, произведенной бригадой рабочих может быть описан уравнением u = -5t?+45t?+600t+300 (ед.), 1
Задача 4.Вычислить производительность труда во время каждого часа работы, при условии, что объем продукции ув течение рабочего дня представлен функцией у = -2t3 +10t2 +50t – 16,
Задача 5. Вычислить производительность труда во время первых 4 часов работы, если объем продукции у в течение рабочего дня представлен функцией
у = — t3 +10t2 +40t – 16, t– время, ч.
Задача 6-14. Вычислить производительность труда во время первых t часов работы, если объем продукции у в течение рабочего дня представлен функцией.
у = -2t2 +10t+50, 1 ? t ? 5, t– время, ч.
у = -3t3 +20t2 +100t – 6, 1 ? t ? 3, t– время, ч.
💥 Видео
Предельная производительность труда. Закон убывающей Предельной производительности трудаСкачать

Продуктивность. Увеличение производительности труда.Скачать

АЛГЕБРА С НУЛЯ — Что такое Производная?Скачать

Производительность труда. Трудозатраты. ТрудоемкостьСкачать

Как работать с формулами работы, производительности труда и времени. Как решать задачи. Часть 22.Скачать

Производительность труда. Понятие и методы расчетаСкачать

Математика. Производительность труда. Задача про количество ям.Скачать

Лекция Экономика предприятия - Персонал предприятия, производительность трудаСкачать

Решение задач в Microsoft Excel. Определение оптимального объёма производстваСкачать

Повышение производительности труда на примере кондитерского производстваСкачать

Принципы повышения производительности труда на производственном предприятии для начинающихСкачать

О производительности трудаСкачать

Факторы повышения производительности трудаСкачать

6.2.2. Средняя и предельная производительность трудаСкачать

Статистика использования рабочего времени и производительности трудаСкачать

Производительность труда | Показатель развития экономикиСкачать

Технология производства – метод повышения производительности труда и инструмент управления компаниейСкачать

Статистика использования рабочего времени и производительности трудаСкачать