Если обе части уравнения умножить или разделить на одно и то же положительное число

Два уравнения называют равносильными, если они имеют одно и тоже множество корней.

Свойства уравнений

• Если к обеим частям данного уравнения прибавить (или из обеих частей вычесть) одно и то же число, то получим уравнение, равносильное данному.
• Если какое-либо слагаемое перенести из одной части уравнения в другую, изменив при этом его знак на противоположный, то получим уравнение, равносильное данному.
• Если обе части уравнения умножить (разделить) на одно и то же отличное от нуля число, то получим уравнение, равносильное данному

Линейное уравнение

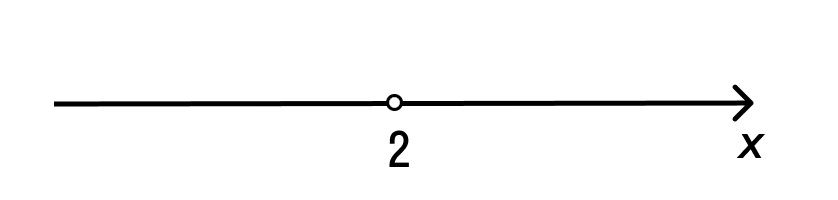
Уравнение вида , где — переменная, и некоторые числа, называют линейным уравнением с одной переменной.

Значения и
Корни уравнения		-любое число	корней нет

Одночлены и многочлены

Одночлены

• Выражения, являющиеся произведениями чисел, переменных и их степеней, называют одночленами.
• Одночлен, содержащий только один отличный от нуля числовой множитель, стоящий на первом месте, а все остальные множители которого — степени с разными основаниями, называют одночленом стандартного вида. К одночленам стандартного вида также относят числа, отличные от нуля, переменные и их степени.
• Числовой множитель одночлена, записанного в стандартном виде, называют коэффициентом одночлена.
• Одночлены, имеющие одинаковые буквенные части, называют подобными. Степенью одночлена называют сумму показателей степеней всех переменных, входящих в него. Степень одночлена, являющегося числом, отличным от нуля, считают равной нулю.
• Нуль-одночлен степени не имеет.

Многочлены

• Выражение, являющееся суммой нескольких одночленов, называют многочленом.
• Одночлены, из которых состоит многочлен, называют членами многочлена.
• Одночлен является частным случаем многочлена. Считают, что такой многочлен состоит из одного члена.

Умножение одночлена на многочлен

Чтобы умножить одночлен на многочлен, надо умножить этот одночлен на каждый член многочлена и полученные произведения сложить.

Умножение многочлена на многочлен

Чтобы умножить многочлен на многочлен, можно каждый член одного многочлена умножить на каждый член другого и полученные произведения сложить.

Формулы сокращенного умножения

Разность квадратов двух выражений

Разность квадратов двух выражений равна произведению разности этих выражений и их суммы:

Произведение разности и суммы двух выражений

Произведение разности двух выражений и их суммы равно разности квадратов этих выражений:

Квадрат суммы и квадрат разности двух выражений

Квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение первого и второго выражений, плюс квадрат второго выражения:

Квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение первого и второго выражений пл юс квадрат второго выражении:

Преобразование многочлена в квадрат суммы или разности двух выражений

позволяют «свернуть» трёхчлен в квадрат двучлена.

Трёхчлен, который можно представить в виде квадрата двучлена, н а зывают полным квадратом.

Сумма и разность кубов двух выражений

Многочлен называют неполным квадратом разности.

Сумма кубов двух выражений равна произведению суммы этих выр а жений и неполного квадрата их разности:

Многочлен называют неполным квадратом суммы.

Разность кубов двух выражений равна произведению разности этих выражений и неполного квадрата их суммы:

Степень. Свойства степени с целым показателем

Свойства степени с целым показателем

Для любого и любых целых выполняются равенства:

Для любых , и любого целого выполняются равенства:

Функция. Область определения и область значений функции

Функция

Правило, с помощью которого по каждому значению независимой переменной можно найти единственное значение зависимой переменной, называют функцией, а соответствующую зависимость одной п e ременной от другой — функциональной.
Обычно независимую переменную обозначают , зависимую обозначают , функцию(правило) — .
Независимую переменную называют аргументом функции. Значение зависимой переменной называют значением функции.
Тогда функциональную зависимость обозначают .
Значения, которые принимает аргумент, образуют область определения функции. Все значения, которые принимает зависимая переменная, образуют область значений функции.

Способы задания функции

Описательный, табличный, с помощью формулы, графический.

График функции

Графиком функции называют геометрическую фигуру, состоящую из всех тех и только тех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты — соответствующим значениям функции.

Линейная функция, её график и свойства

• Функцию, которую можно задать формулой вида , где и — некоторые числа, — независимая переменная, называют линейной.
• Графиком линейной функции является прямая.
• Линейную функцию, заданную формулой , где , называют прямой пропорциональностью.

Системы линейных уравнений с двумя переменными

Уравнение с двумя переменными

Пару значений переменных, обращающую уравнение с двумя переменными в верное равенство, называют решением уравнения с двумя переменными.

Решить уравнение с двумя переменными — значит найти все его решения или показать, что оно не имеет решений.

Графиком уравнения с двумя переменными называют геометрическую фигуру, состоящую из всех тех и только тех точек координатной плоскости, координаты которых (пары чисел) являются решениями данного уравнения.

Если некоторая фигура является графиком уравнения, то выполняются два условия:

• все решения уравнения являются координатами точек, принадлежащих графику;
• координаты любой точки, принадлежащей графику, — это пара чисел, являющаяся решением данного уравнения.

Графический метод решения системы двух линейных уравнений с двумя переменными

Графический метод решения системы уравнений заключается в следующем:

• построить в одной координатной плоскости графики уравнений, входящих в систему;
• найти координаты всех точек пересечения построенных графиков;
• полученные пары чисел и будут искомыми решениями.

Если графиками уравнений, входящих в систему линейных уравнении, являются прямые, то количество решений этой системы зависит от взаимного расположения двух прямых на плоскости:

• если прямые пересекаются, то система имеет единственное решение.
• если прямые совпадают, то система имеет бесконечно много решении.
• если прямые параллельны, то система решений не имеет.

Решение системы двух линейных уравнений с двумя переменными методом подстановки

Чтобы решить систему линейных уравнений методом подстановки, следует:

• выразить из любого уравнения системы одну переменную через другую;
• подставить в уравнение системы вместо этой переменной выражение, полученное на первом шаге;
• решить уравнение с одной переменной, полученное на втором шаге;
• подставить найденное значение переменной в выражение, полученное на первом шаге;
• вычислить значение второй переменной;
• записать ответ.

Решение систем линейных уравнений методом сложения

Чтобы решить систему линейных уравнений методом сложения, следует:

• подобрать такие множители для уравнений, чтобы после преобразований коэффициенты при одной из переменной стали противоположными числами
• сложить почленно левые и правые части уравнений, полученных на первом шаге
• решить уравнение с одной переменной, полученной на втором шаге
• подставить найденное на третьем шаге значение переменной в любое из уравнений исходной системы;
• вычислить значение второй переменной;
• записать ответ.

Видео:Свойства уравнений. Умножение и деление обеих частей уравнения на одно и то же число. Алгебра 7 кл.Скачать

Числовые неравенства и их свойства

теория по математике 📈 неравенства

Числовое неравенство – это неравенство, в котором по обе стороны от знака неравенства содержатся числа или числовые выражения. Результат сравнения записывают с помощью знаков =, .

Например, 24=24; 46>13, 67 –65.

В зависимости от конкретных чисел используется способ сравнения, но существует способ, который охватывает все числа, он основывается на следующем определении.

Способ сравнения чисел

Число а больше числа b, если разность (а – b) является положительным числом; число а меньше числа b, если разность (а – b) является отрицательным числом; число а равно числу b, если разность (а – b ) является равным нулю числом.

Пример №1.

1. 123>118, так как 123–118=5, a 5>0;
2. –15>–65, так как –15–(–65)= –15+65=50, a 50>0
3. 118 Основные свойства числового неравенства
   1. Если обе части верного неравенства умножить или разделить на одно и то же положительное число, то получится верное неравенство.
   2. Если обе части верного неравенства умножить или разделить на одно и то же отрицательное числои изменить знак неравенства на противоположный, то получится верное неравенство.
   3. Если a и b положительные числа, причем a Пример №2.
      1. Дано неравенство 45>21. Если обе части умножим на одно и то же положительное число, например, 10, то получится верное неравенство 450>210.
      2. Дано неравенство 95>35. Обе части разделим на одно и то же отрицательное число (–5), при этом знак неравенства изменим на противоположный: 95:(–5) Алла Василевская | Просмотров: 3.7k | Оценить:

      Видео:Теория. Умножение и деление обеих частей уравнения (5-8 класс)Скачать

      

      Решение линейных неравенств

      

      О чем эта статья:

      Видео:Решение уравнений, 6 классСкачать

      

      Основные понятия

      Алгебра не всем дается легко с первого раза. Чтобы не запутаться во всех темах и правилах, важно изучать темы последовательно и по чуть-чуть. Сегодня узнаем, как решать линейные неравенства.

      Неравенство — это алгебраическое выражение, в котором используются знаки ≠, , ≤, ≥.

      Линейные неравенства — это неравенства вида:

      где a и b — любые числа, a ≠ 0, x — неизвестная переменная. Как решаются неравенства рассмотрим далее в статье.

      Решение — значение переменной, при котором неравенство становится верным.

      Решить неравенство значит найти все значения переменной, при которой неравенство верное.

      Видео:ЛИНЕЙНЫЕ УРАВНЕНИЯ - Как решать линейные уравнения // Подготовка к ЕГЭ по МатематикеСкачать

      

      Типы неравенств

      1. Строгие — используют только больше (>) или меньше ( b — это значит, что a больше, чем b.
      2. a > b и b > и

      Видео:КАК РЕШАТЬ УРАВНЕНИЯ С ОДНОЙ ПЕРЕМЕННОЙ? · Алгебра Математика 7 классСкачать

      

      Линейные неравенства: свойства и правила

      Вспомним свойства числовых неравенств:

      1. Если а > b , то b а.
      2. Если а > b и b > c, то а > c. И также если а b, то а + c > b+ c (и а – c > b – c).

      Если же а b и c > d, то а + c > b + d.

   Если а 8 почленно вычесть 3 > 2, получим верный ответ 9 > 6. Если из 12 > 8 почленно вычесть 7 > 2, то полученное будет неверным.

   Если а d, то а – c b, m — положительное число, то mа > mb и
   

Обе части можно умножить или разделить на одно положительное число (знак при этом остаётся тем же).

Если же а > b, n — отрицательное число, то nа

Обе части можно умножить или разделить на одно отрицательное число, при этом знак неравенства поменять на противоположный.

1. Если а > b и c > d, где а, b, c, d > 0, то аc > bd.

Если а 0, то аc b, где а, b > 0, то а2 > b2, и если а b, где а, b > 0, то
b» height=»45″ src=»https://lh5.googleusercontent.com/MuRDPQeqxIZvVG_mHVaktFp6nlIEEbz8zdRs1ZW8CZbZacJrS4aKzrDyhKxXpJvc35TSAgiRpqr-63sGzL9_sPU80vFhR0ZDAmSmRFZtwEldDkWRttfSGuaJJIb7xWxZDugU3xTt»>

Решением неравенства с одной переменной называется значение переменной, которое трансформирует его в верное числовое неравенство.

Чтобы упростить процесс нахождения корней неравенства, нужно провести равносильные преобразования — то заменить данное неравенство более простым. При этом все решения должны быть сохранены без возникновения посторонних корней.

Свойства выше помогут нам использовать следующие правила.

Видео:Решение простых уравнений. Что значит решить уравнение? Как проверить решение уравнения?Скачать

Правила линейных неравенств

1. Любой член можно перенести из одной части в другую с противоположным знаком. Знак неравенства при этом не меняется.

• 2x − 3 > 6 ⇒ 2x > 6 + 3 ⇒ 2x > 9.

1. Обе части можно умножить или разделить на одно положительное число. Знак неравенства при этом не меняется.

• Умножим обе части на пять 2x > 9 ⇒ 10x > 45.

1. Обе части можно умножить или разделить на одно отрицательное число. Знак неравенства при этом меняется на противоположный.

• Разделим обе части на минус два 2x > 9 ⇒ 2x : (–2) > 9 : (–2) ⇒ x
  

  Видео:Решение уравнений в несколько действий. Как объяснить ребенку решение уравнений?Скачать

  

  Решение линейных неравенств

  Линейные неравенства с одной переменной x выглядят так:

  где a и b — действительные числа. А на месте x может быть обычное число.

  Видео:Как решают уравнения в России и СШАСкачать

  

  Равносильные преобразования

  Для решения ax + b , ≥) нужно применить равносильные преобразования неравенства. Рассмотрим два случая: когда коэффициент равен и не равен нулю.

  Алгоритм решения ax + b , ≥) является верным, когда исходное имеет решение при любом значении. Неверно тогда, когда исходное не имеет решений.

  Рассмотрим пример: 0 * x + 5 > 0.

  Как решаем:

  • Данное неравенство 0 * x + 5 > 0 может принимать любое значение x.
  • Получается верное числовое неравенство 5 > 0. Значит его решением может быть любое число.

  Видео:Решение уравнений ( подобные слагаемые ) . 6 класс .Скачать

  

  Метод интервалов

  Метод интервалов можно применять для линейных неравенств, когда значение коэффициента x не равно нулю.

  Метод интервалов заключается в следующем:

  • вводим функцию y = ax + b;
  • ищем нули для разбиения области определения на промежутки;
  • отмечаем полученные корни на координатной прямой;
  • определяем знаки и отмечаем их на интервалах.

  Алгоритм решения ax + b , ≥) при a ≠ 0 с использованием метода интервалов:

  • найдем нули функции y = ax + b для решения уравнения ax + b = 0.

  Если a ≠ 0, тогда решением будет единственный корень — х₀;

  • начертим координатную прямую с изображением точки с координатой х₀, при строгом неравенстве точку рисуем выколотой, при нестрогом — закрашенной;
  • определим знаки функции y = ax + b на промежутках.

  Для этого найдем значения функции в точках на промежутке;

  если решение неравенства со знаками > или ≥ — добавляем штриховку над положительным промежутком на координатной прямой, если 0.

  Как решаем:

  В соответствии с алгоритмом, сначала найдем корень уравнения − 6x + 12 = 0,

  Изобразим координатную прямую с отмеченной выколотой точкой, так как неравенство является строгим.

  

  Определим знаки на промежутках.

  Чтобы определить на промежутке (−∞, 2), необходимо вычислить функцию y = −6x + 12 при х = 1. Получается, что −6 * 1 + 12 = 6, 6 > 0. Знак на промежутке является положительным.

  Определяем знак на промежутке (2, + ∞) , тогда подставляем значение х = 3. Получится, что −6 * 3 + 12 = − 6, − 6

  Видео:16. Решение уравненийСкачать

  

  Графический способ

  Смысл графического решения неравенств заключается в том, чтобы найти промежутки, которые необходимо изобразить на графике.

  Алгоритм решения y = ax + b графическим способом

  • во время решения ax + b 0 определить промежуток, где график изображается выше Ох;
  • во время решения ax + b ≥ 0 определить промежуток, где график находится выше оси Ох или совпадает.

  Рассмотрим пример: −5 * x − √3 > 0.

  Как решаем

  • Так как коэффициент при x отрицательный, данная прямая является убывающей.
  • Координаты точки пересечения с Ох равны (−√3 : 5; 0).
  • Неравенство имеет знак >, значит нужно обратить внимание на промежуток выше оси Ох.
  • Поэтому открытый числовой луч (−∞, −√3 : 5) будет решением.

  Ответ: (−∞, −√3 : 5) или x

  💡 Видео

  Линейное уравнение с одним неизвестным.Скачать

  

  Система иррациональных уравнений #3Скачать

  

  Тема:Уравнение и его корни.стр.25. Алгебра 7. Макарычев. Под ред. Теляковского.Скачать

  

  Решение уравнений. Как переносить слагаемые из одной части уравнения в другую. Математика 6 классСкачать

  

  Равносильные уравнения. Рациональные уравнения - 8 класс алгебраСкачать

  

  Алгебра 10 класс (Урок№19 - Равносильные уравнения и неравенства.)Скачать

  

  Система иррациональных уравнений #4Скачать

  

  Как решать неравенства? Часть 1| МатематикаСкачать

  

  ЕГЭ. Промежуточный срез № 5 «Повторение и обобщение» по пройденным темамСкачать

  

  КАК РЕШАТЬ ЛИНЕЙНЫЕ УРАВНЕНИЯ С ОДНОЙ ПЕРЕМЕННОЙ? · Алгебра Математика 7 классСкачать