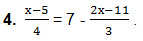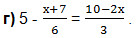Если обе части уравнения умножить или разделить на одно и то же отличное от нуля

Видео:Решение уравнений, 6 классСкачать

Если обе части уравнения умножить или разделить на одно и то же отличное от нуля

Два уравнения называют равносильными, если они имеют одно и тоже множество корней.

Свойства уравнений

• Если к обеим частям данного уравнения прибавить (или из обеих частей вычесть) одно и то же число, то получим уравнение, равносильное данному.
• Если какое-либо слагаемое перенести из одной части уравнения в другую, изменив при этом его знак на противоположный, то получим уравнение, равносильное данному.
• Если обе части уравнения умножить (разделить) на одно и то же отличное от нуля число, то получим уравнение, равносильное данному

Линейное уравнение

Уравнение вида , где — переменная, и некоторые числа, называют линейным уравнением с одной переменной.

Значения и
Корни уравнения		-любое число	корней нет

Одночлены и многочлены

Одночлены

• Выражения, являющиеся произведениями чисел, переменных и их степеней, называют одночленами.
• Одночлен, содержащий только один отличный от нуля числовой множитель, стоящий на первом месте, а все остальные множители которого — степени с разными основаниями, называют одночленом стандартного вида. К одночленам стандартного вида также относят числа, отличные от нуля, переменные и их степени.
• Числовой множитель одночлена, записанного в стандартном виде, называют коэффициентом одночлена.
• Одночлены, имеющие одинаковые буквенные части, называют подобными. Степенью одночлена называют сумму показателей степеней всех переменных, входящих в него. Степень одночлена, являющегося числом, отличным от нуля, считают равной нулю.
• Нуль-одночлен степени не имеет.

Многочлены

• Выражение, являющееся суммой нескольких одночленов, называют многочленом.
• Одночлены, из которых состоит многочлен, называют членами многочлена.
• Одночлен является частным случаем многочлена. Считают, что такой многочлен состоит из одного члена.

Умножение одночлена на многочлен

Чтобы умножить одночлен на многочлен, надо умножить этот одночлен на каждый член многочлена и полученные произведения сложить.

Умножение многочлена на многочлен

Чтобы умножить многочлен на многочлен, можно каждый член одного многочлена умножить на каждый член другого и полученные произведения сложить.

Формулы сокращенного умножения

Разность квадратов двух выражений

Разность квадратов двух выражений равна произведению разности этих выражений и их суммы:

Произведение разности и суммы двух выражений

Произведение разности двух выражений и их суммы равно разности квадратов этих выражений:

Квадрат суммы и квадрат разности двух выражений

Квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение первого и второго выражений, плюс квадрат второго выражения:

Квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение первого и второго выражений пл юс квадрат второго выражении:

Преобразование многочлена в квадрат суммы или разности двух выражений

позволяют «свернуть» трёхчлен в квадрат двучлена.

Трёхчлен, который можно представить в виде квадрата двучлена, н а зывают полным квадратом.

Сумма и разность кубов двух выражений

Многочлен называют неполным квадратом разности.

Сумма кубов двух выражений равна произведению суммы этих выр а жений и неполного квадрата их разности:

Многочлен называют неполным квадратом суммы.

Разность кубов двух выражений равна произведению разности этих выражений и неполного квадрата их суммы:

Степень. Свойства степени с целым показателем

Свойства степени с целым показателем

Для любого и любых целых выполняются равенства:

Для любых , и любого целого выполняются равенства:

Функция. Область определения и область значений функции

Функция

Правило, с помощью которого по каждому значению независимой переменной можно найти единственное значение зависимой переменной, называют функцией, а соответствующую зависимость одной п e ременной от другой — функциональной.
Обычно независимую переменную обозначают , зависимую обозначают , функцию(правило) — .
Независимую переменную называют аргументом функции. Значение зависимой переменной называют значением функции.
Тогда функциональную зависимость обозначают .
Значения, которые принимает аргумент, образуют область определения функции. Все значения, которые принимает зависимая переменная, образуют область значений функции.

Способы задания функции

Описательный, табличный, с помощью формулы, графический.

График функции

Графиком функции называют геометрическую фигуру, состоящую из всех тех и только тех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты — соответствующим значениям функции.

Линейная функция, её график и свойства

• Функцию, которую можно задать формулой вида , где и — некоторые числа, — независимая переменная, называют линейной.
• Графиком линейной функции является прямая.
• Линейную функцию, заданную формулой , где , называют прямой пропорциональностью.

Системы линейных уравнений с двумя переменными

Уравнение с двумя переменными

Пару значений переменных, обращающую уравнение с двумя переменными в верное равенство, называют решением уравнения с двумя переменными.

Решить уравнение с двумя переменными — значит найти все его решения или показать, что оно не имеет решений.

Графиком уравнения с двумя переменными называют геометрическую фигуру, состоящую из всех тех и только тех точек координатной плоскости, координаты которых (пары чисел) являются решениями данного уравнения.

Если некоторая фигура является графиком уравнения, то выполняются два условия:

• все решения уравнения являются координатами точек, принадлежащих графику;
• координаты любой точки, принадлежащей графику, — это пара чисел, являющаяся решением данного уравнения.

Графический метод решения системы двух линейных уравнений с двумя переменными

Графический метод решения системы уравнений заключается в следующем:

• построить в одной координатной плоскости графики уравнений, входящих в систему;
• найти координаты всех точек пересечения построенных графиков;
• полученные пары чисел и будут искомыми решениями.

Если графиками уравнений, входящих в систему линейных уравнении, являются прямые, то количество решений этой системы зависит от взаимного расположения двух прямых на плоскости:

• если прямые пересекаются, то система имеет единственное решение.
• если прямые совпадают, то система имеет бесконечно много решении.
• если прямые параллельны, то система решений не имеет.

Решение системы двух линейных уравнений с двумя переменными методом подстановки

Чтобы решить систему линейных уравнений методом подстановки, следует:

• выразить из любого уравнения системы одну переменную через другую;
• подставить в уравнение системы вместо этой переменной выражение, полученное на первом шаге;
• решить уравнение с одной переменной, полученное на втором шаге;
• подставить найденное значение переменной в выражение, полученное на первом шаге;
• вычислить значение второй переменной;
• записать ответ.

Решение систем линейных уравнений методом сложения

Чтобы решить систему линейных уравнений методом сложения, следует:

• подобрать такие множители для уравнений, чтобы после преобразований коэффициенты при одной из переменной стали противоположными числами
• сложить почленно левые и правые части уравнений, полученных на первом шаге
• решить уравнение с одной переменной, полученной на втором шаге
• подставить найденное на третьем шаге значение переменной в любое из уравнений исходной системы;
• вычислить значение второй переменной;
• записать ответ.

Видео:Равносильные уравненияСкачать

Алгебра и начала математического анализа. 10 класс

Тезаурус

Уравнения, имеющие одно и то же множество корней, называются равносильными.

Если при переходе от одного уравнения к другому потери корней не происходит, то второе уравнение называют следствием первого уравнения. Иначе, если все корни первого уравнения являются корнями второго уравнения, то второе уравнение называется следствием первого уравнения.

Неравенства, имеющие одно и то же множество решений, называют равносильными. Неравенства, не имеющие решений, также являются равносильными.

Определение. Областью определения уравнения f(х) = g(х) или областью допустимых значений переменной (ОДЗ) называют множество тех значений переменной х, при которых одновременно имеют смысл выражения f(х) и g(х).

Теорема 1. Если какой-либо член уравнения перенести из одной части уравнения в другую с противоположным знаком, то получится уравнение, равносильное данному.

Теорема 2. Если обе части уравнения возвести в одну и ту же нечетную степень, то получится уравнение, равносильное данному.

Теорема 3. Показательное уравнение аf(x) = аg(x) (где а > 0, a ≠ 1)

равносильно уравнению f(x) = g(х).

Теорема 4. Если обе части уравнения f(x) = g(х) умножить на одно и то же выражение h(х), которое:

а) имеет смысл всюду в области определения (в области допустимых значений) уравнения f(x) = g(х)

б) нигде в этой области не обращается в 0, то получится уравнение f(x)h(x) = g(x)h(x), равносильное данному в его ОДЗ.

Следствие теоремы 4: если обе части уравнения умножить или разделить на одно и то же отличное от нуля число, то получится уравнение, равносильное данному.

Теорема 5. Если обе части уравнения f(x) = g(х) неотрицательны в ОДЗ уравнения, то после возведения обеих его частей в одну и ту же четную степень n получится уравнение (f(x))n = (g(x))n равносильное данному в его ОДЗ.

Список литературы

• Колягин Ю.М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 10 кл. – М.: Просвещение, 2014.

• Шабунин М.И., Ткачева М.В., Федорова Н.Е. Дидактические материалы Алгебра и начала математического анализа (базовый и профильный уровни) 10 кл. – М.: Просвещение, 2017.

Видео:Линейное уравнение с одним неизвестным.Скачать

Рациональные уравнения с примерами решения

Содержание:

Видео:линейные уравненияСкачать

Рациональные уравнения. Равносильные уравнения

два уравнения называют равносильными, если они имеют одни и те же корни. Равносильными считают и те уравнения, которые корней не имеют.

Так, например, равносильными будут уравнения

Уравнения — не равносильны, так как корнем первого уравнения является число 10, а корнем второго — число 9.

Ранее, в 7 классе, вы знакомились со свойствами, которые преобразуют уравнения в равносильные им уравнения.

1) Если в любой части уравнения раскрыть скобки или привести подобные слагаемые, то получим уравнение, равносильное данному;

2) если в уравнении перенести слагаемое из одной части в другую, изменив его знак на противоположный, то получим уравнение, равносильное данному;

3) если обе части уравнения умножить или разделить на одно и то же отличное от нуля число, то получим уравнение, равносильное данному.

Левая и правая части каждого из них являются рациональными выражениями.

Уравнении, левая и правая части которых являются рациональными выражениями, называют рациональными уравнениями.

В первых двух из записанных выше уравнений левая и правая части являются целыми выражениями. Такие уравнения называют целыми рациональными уравнениями. Если хотя бы одна часть уравнения — дробное выражение, то его называют дробным рациональным уравнением. Третье из записанных выше уравнений является дробным рациональным.

Как решать целые рациональные уравнения, мы рассмотрели при изучении математики в предыдущих классах. Рассмотрим теперь, как решать дробные рациональные уравнения, то есть уравнения с переменной в знаменателе.

Применение условия равенства дроби нулю

Напомним, что когда

Пример №202

Решите уравнение

Решение:

С помощью тождественных преобразований и свойств уравнений приведем уравнение к виду где и — целые рациональные выражения. Имеем:

Окончательно получим уравнение:

Чтобы дробь равнялась нулю, нужно, чтобы числитель равнялся нулю, а знаменатель не равнялся нулю.

Тогда откуда При знаменатель Следовательно, — единственный корень уравнения.

Решение последнего, равносильного данному, уравнения, учитывая условие равенства дроби нулю, удобно записывать так:

Значит, решая дробное рациональное уравнение, можно:

1) с помощью тождественных преобразований привести уравнение к виду

2) приравнять числитель к нулю и решить полученное целое уравнение;

3) исключить из его корней те, при которых знаменатель равен нулю, и записать ответ.

Использование основного свойства пропорции

Если то где

Пример №203

Решите уравнение

Решение:

Найдем область допустимых значений (ОДЗ) переменной в уравнении. Так как знаменатели дробей не могут равняться нулю, то Имеем: то есть ОДЗ переменной содержит все числа, кроме 1 и 2.

Сложив выражения в правой части уравнения, приведем его к виду: получив пропорцию:

По основному свойству пропорции имеем:

Решим это уравнение:

откуда

Так как число 4 принадлежит ОДЗ переменной исходного уравнения, то 4 является его корнем.

Запись решения, чтобы не забыть учесть ОДЗ, удобно закончить так:

Таким образом, для решения дробного рационального уравнения можно:

1) найти область допустимых значений (ОДЗ) переменной в уравнении;

2) привести уравнение к виду

3) записать целое уравнение и решить его;

4) исключить из полученных корней те, которые не принадлежат ОДЗ, и записать ответ.

Метод умножения обеих частей уравнения на общий знаменатель дробей

Пример №204

Решите уравнение

Решение:

Найдем ОДЗ переменной и простейший общий знаменатель всех дробей уравнения, разложив знаменатели на множители:

Областью допустимых значений переменной будут те значения при которых то есть все значения кроме чисел А простейшим общим знаменателем будет выражение

Умножим обе части уравнения на это выражение:

Получим: а после упрощения: то есть откуда или

Число 0 не принадлежит ОДЗ переменной исходного уравнения, поэтому не является его корнем.

Следовательно, число 12 — единственный корень уравнения. Ответ. 12.

Решая дробное рациональное уравнение, можно:

3) умножить обе части уравнения на этот общий знаменатель;

4) решить полученное целое уравнение;

5) исключить из его корней те, которые не принадлежат ОДЗ переменной уравнения, и записать ответ.

Пример №205

Являются ли равносильными уравнения

Решение:

Поскольку уравнения являются равносильными в случае, когда они имеют одни и те же, или не имеют корней, найдем корни данных уравнений.

Первое уравнение имеет единственный корень а второе — два корня (решите уравнения самостоятельно). Следовательно, уравнения не являются равносильными.

Степень с целым показателем

Напомним, что в 7 классе мы изучали степень с натуральным показателем. По определению:

где — натуральное число,

В математике, а также при решении задач практического содержания, например в физике или химии, встречаются степени, показатель которых равен нулю или является целым отрицательным числом. Степень с отрицательным показателем можно встретить и в научной или справочной литературе. Например, массу атома гелия записывают так: кг. Как понимать смысл записи

Рассмотрим степени числа 3 с показателями — это соответственно

В этой строке каждое следующее число втрое больше предыдущего. Продолжим строку в противоположном направлении, уменьшая каждый раз показатель степени на 1. Получим:

Число должно быть втрое меньше числа равного числу 3. Но втрое меньшим числа 3 является число 1, следовательно, Равенство справедливо для любого основания при условии, что

Нулевая степень отличного от нуля числа а равна единице, то есть при

Вернемся к строке со степенями числа 3, где слева от числа записано число Это число втрое меньше, чем 1, то есть равно Следовательно, Рассуждая аналогично получаем: и т. д.

Приходим к следующему определению степени с целым отрицательным показателем:

если натуральное число, то

Видео:Решение простых уравнений. Что значит решить уравнение? Как проверить решение уравнения?Скачать

6.5.1. Линейное уравнение с одной переменной

У очень многих школьников возникает вопрос — как решить уравнение с x. Что значит решить уравнение и как найти корень уравнения. Давайте рассмотрим основную схему решения обычного уравнения, называемого линейным, с одной переменной.

Видео:Равносильность уравнений. Уравнение – следствие | Алгебра 11 класс #24 | ИнфоурокСкачать

Правила и определения

Основные правила и определения для линейного уравнения с одной переменной.

• Равенство с переменной называют уравнением.
• Решить уравнение – значит найти множество его корней. Уравнение может иметь один, два, несколько, множество корней или не иметь их вовсе.
• Каждое значение переменной, при котором данное уравнение превращается в верное равенство, называется корнем уравнения.
• Уравнения, имеющие одни и те же корни, называются равносильными уравнениями.
• Любое слагаемое уравнения можно перенести из одной части равенства в другую, изменив при этом знак слагаемого на противоположный.
• Если обе части уравнения умножить или разделить на одно и то же отличное от нуля число, то получится уравнение, равносильное данному уравнению.

Видео:Равносильные уравнения. Рациональные уравнения - 8 класс алгебраСкачать

Примеры. Решить уравнение.

Уравнение 1

1. 1,5х-0,3х = -2-4. Собрали слагаемые, содержащие переменную, в левой части равенства, а свободные члены – в правой части равенства. При этом применяли свойство: любое слагаемое уравнения можно перенести из одной части равенства в другую, изменив при этом знак слагаемого на противоположный.
2. 1,2х = -6. Привели подобные слагаемые по правилу: чтобы привести подобные слагаемые, надо сложить их коэффициенты и полученный результат умножить на их общую буквенную часть (т.е. к полученному результату приписать их общую буквенную часть).
3. х = -6 : 1,2. Обе части равенства разделили на коэффициент при переменной, так как если обе части уравнения умножить или разделить на одно и то же отличное от нуля число, то получится уравнение, равносильное данному уравнению.
4. х = -5. Делили по правилу деления десятичной дроби на десятичную дробь:
5. чтобы разделить число на десятичную дробь, нужно перенести запятые в делимом и делителе на столько цифр вправо, сколько их стоит после запятой в делителе, а затем выполнить деление на натуральное число: 6 : 1,2 = 60 : 12 = 5.

Ответ: 5.

Уравнение 2

3∙(2х-9) = 4∙(х-4).

1. 6х-27 = 4х-16. Раскрыли скобки, используя распределительный закон умножения относительно вычитания: чтобы разность двух чисел умножить на третье число, можно отдельно уменьшаемое и отдельно вычитаемое умножить на третье число, а затем из первого результата вычесть второй результат, т.е. (a-b) ∙ c = a ∙ c-b ∙ c.
2. 6х-4х = -16+27. Собрали слагаемые, содержащие переменную, в левой части равенства, а свободные члены – в правой части равенства. При этом применяли свойство: любое слагаемое уравнения можно перенести из одной части равенства в другую, изменив при этом знак слагаемого на противоположный.
3. 2х = 11. Привели подобные слагаемые по правилу: чтобы привести подобные слагаемые, надо сложить их коэффициенты и полученный результат умножить на их общую буквенную часть (т.е. к полученному результату приписать их общую буквенную часть).
4. х = 11 : 2. Обе части равенства разделили на коэффициент при переменной, так как если обе части уравнения умножить или разделить на одно и то же отличное от нуля число, то получится уравнение, равносильное данному уравнению.

Ответ: 5,5.

Уравнение 3

1. 7х-3-2х = х-9. Раскрыли скобки по правилу раскрытия скобок, перед которыми стоит знак «-»: если перед скобками стоит знак «-», то убираем скобки, знак «-» и записываем слагаемые, стоявшие в скобках, с противоположными знаками.
2. 7х-2х-х = -9+3. Собрали слагаемые, содержащие переменную, в левой части равенства, а свободные члены – в правой части равенства. При этом применяли свойство: любое слагаемое уравнения можно перенести из одной части равенства в другую, изменив при этом знак слагаемого на противоположный.
3. 4х = -6. Привели подобные слагаемые по правилу: чтобы привести подобные слагаемые, надо сложить их коэффициенты и полученный результат умножить на их общую буквенную часть (т.е. к полученному результату приписать их общую буквенную часть).
4. х = -6 : 4. Обе части равенства разделили на коэффициент при переменной, так как если обе части уравнения умножить или разделить на одно и то же отличное от нуля число, то получится уравнение, равносильное данному уравнению.

Ответ: -1,5.

Уравнение 4

1. 3 ∙ (х-5) = 7 ∙ 12 — 4 ∙ (2х-11). Умножили обе части равенства на 12 – наименьший общий знаменатель для знаменателей данных дробей.
2. 3х-15 = 84-8х+44. Раскрыли скобки, используя распределительный закон умножения относительно вычитания: чтобы разность двух чисел умножить на третье число, можно отдельно уменьшаемое и отдельно вычитаемое умножить на третье число, а затем из первого результата вычесть второй результат, т.е. (a-b) ∙ c = a ∙ c-b ∙ c.
3. 3х+8х = 84+44+15. Собрали слагаемые, содержащие переменную, в левой части равенства, а свободные члены – в правой части равенства. При этом применяли свойство: любое слагаемое уравнения можно перенести из одной части равенства в другую, изменив при этом знак слагаемого на противоположный.
4. 11х = 143. Привели подобные слагаемые по правилу: чтобы привести подобные слагаемые, надо сложить их коэффициенты и полученный результат умножить на их общую буквенную часть (т.е. к полученному результату приписать их общую буквенную часть).
5. х = 143 : 11. Обе части равенства разделили на коэффициент при переменной, так как если обе части уравнения умножить или разделить на одно и то же отличное от нуля число, то получится уравнение, равносильное данному уравнению.

Ответ: 13.

Видео:Алгебра 10 класс (Урок№19 - Равносильные уравнения и неравенства.)Скачать

Уравнения для самостоятельного решения

Решить самостоятельно уравнения:

а) 3-2,6х = 5х+1,48;

б) 1,6 · (х+5) = 4 · (4,5-0,6х);

в) 9х- (6х+2,5) = — (х-5,5);

5а) 0,2; 5б) 2,5; 5в) 2; 5г) -1.

Видео:Тема:Уравнение и его корни.стр.25. Алгебра 7. Макарычев. Под ред. Теляковского.Скачать

Важные выводы

Итак, для того, чтобы решить уравнение — надо определить его переменную, перенести неизвестную переменную в левую часть уравнения, а известные — в праву. При необходимости упростить левую и правую части и затем найти корень уравнения.

📽️ Видео

Как решать линейные уравнения.Скачать

Решение уравнений 2Скачать

Как решать неравенства? Часть 1| МатематикаСкачать

КАК РЕШИТЬ УРАВНЕНИЕ С ДРОБЯМИ, СВОДЯЩЕЕСЯ К ЛИНЕЙНОМУ? Примеры | АЛГЕБРА 7 классСкачать

Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Уравнение вида ах = с 6 класс Часть 2 Теперь учимся высвобождать переменную от множителя.Скачать

Урок 6 УРАВНЕНИЕ И ЕГО КОРНИ 7 КЛАСССкачать

Равносильные уравнения. Совокупность уравнений. Подготовка к ГВЭ11 + ЕГЭ 2021 по математике #41Скачать

Решение уравнений в несколько действий. Как объяснить ребенку решение уравнений?Скачать

РАВНОСИЛЬНЫЕ УРАВНЕНИЯ И ИХ СВОЙСТВА. Видеоурок | АЛГЕБРА 7 классСкачать

Математика 6 класс (Урок№50 - Уравнения. Часть 2.)Скачать