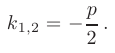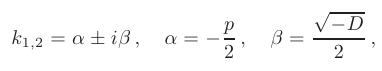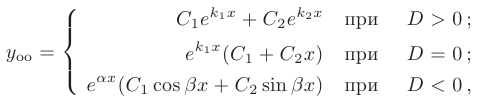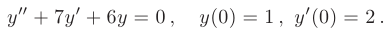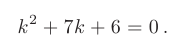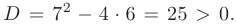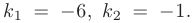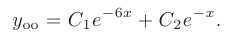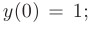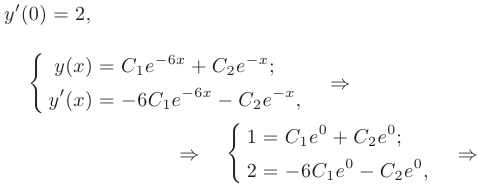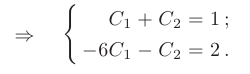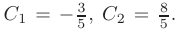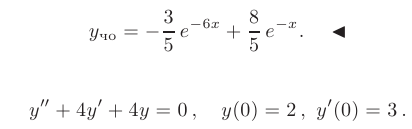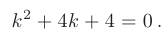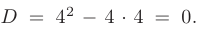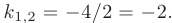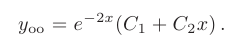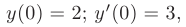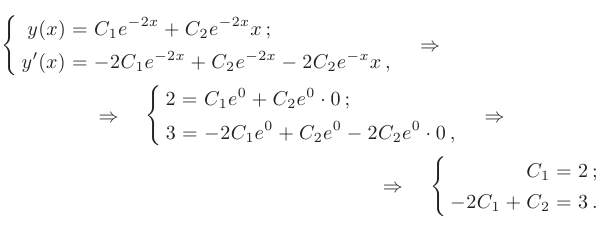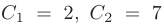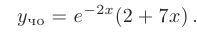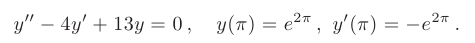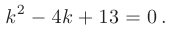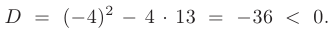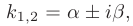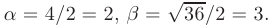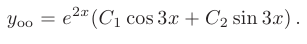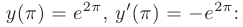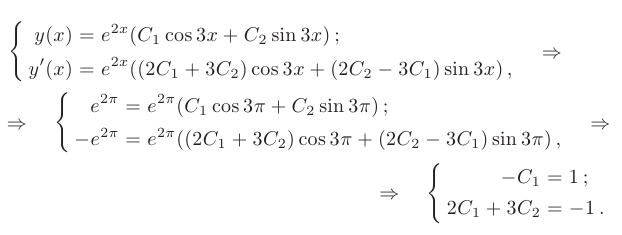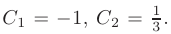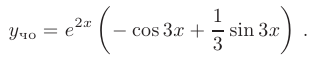Однородные линейные дифференциальные уравнения второго порядка с постоянными коэффициентами имеют вид
где p и q — действительные числа. Рассмотрим на примерах, как решаются однородные дифференциальные уравнения второго порядка с постоянными коэффициентами.
Решение линейного однородного однородного дифференциального уравнения второго порядка зависит от корней характеристического уравнения. Характеристическое уравнение — это уравнение k²+pk+q=0.
1) Если корни характеристического уравнения — различные действительные числа:
то общее решение линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами имеет вид
2) Если корни характеристического уравнения — равные действительные числа
(например, при дискриминанте, равном нулю), то общее решение однородного дифференциального уравнения второго порядка есть
3) Если корни характеристического уравнения — комплексные числа
(например, при дискриминанте, равном отрицательному числу), то общее решение однородного дифференциального уравнения второго порядка записывается в виде
Примеры решения линейных однородных дифференциальных уравнений второго порядка с постоянными коэффициентами
Найти общие решения однородных дифференциальных уравнений второго порядка:
Составляем характеристическое уравнение: k²-7k+12=0. Его дискриминант D=b²-4ac=1>0, поэтому корни — различные действительные числа.
Отсюда, общее решение этого однородного ДУ 2-го порядка есть
Составим и решим характеристическое уравнение:
Корни действительные и различные. Отсюда имеем общее решение данного однородного дифференциального уравнения:
В этом случае характеристическое уравнение
Корни различны и действительны. Поэтому общее решение однородного дифференциального уравнения 2-го порядка здесь
Поскольку корни действительны и равны, для этого дифференциального уравнения общее решение записываем как
Характеристическое уравнение здесь
Так как дискриминант — отрицательное число, корни характеристического уравнения — комплексные числа.
Общее решение этого однородного дифференциального уравнения второго порядка имеет вид
Отсюда находим общее решение данного диф. уравнения:
Примеры для самопроверки.
Найти общее решение однородных дифференциальных уравнений второго порядка с постоянными коэффициентами:
- Линейное однородное дифференциальное уравнение второго порядка с постоянными коэффициентами в математике
- Линейное однородное дифференциальное уравнение второго порядка с постоянными коэффициентами
- Пример:
- Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами
- Основные понятия о линейных дифференциальных уравнениях второго порядка и их решениях
- Линейное однородное дифференциальное уравнение второго порядка и его решение
- Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами: теория и практика
- Решить линейное однородное дифференциальное уравнение с постоянными коэффициентами самостоятельно, а затем посмотреть решение
- 🔥 Видео
Видео:2194. ЛОДУ. Корни характеристического уравнения комплексные и действительные.Скачать

Линейное однородное дифференциальное уравнение второго порядка с постоянными коэффициентами в математике
Линейное однородное дифференциальное уравнение второго порядка с постоянными коэффициентами
Рассмотрим метод решения линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами:
Линейной комбинацией функций 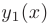
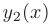
где 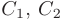
Функции 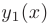
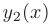
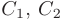
Теорема 7.2. Если 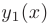
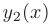
Следовательно, чтобы найти общее решение линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами, надо знать два его частных линейно независимых решения: 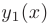
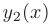
Будем искать частное решение дифференциального уравнения в виде 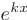
Очевидно, функция 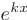
которое называется характеристическиль уравнением исходного дифференциального уравнения.
Как известно, для корней данного квадратного трехчлена возможны три случая.
- Если дискриминант больше нуля
, то корни характеристического уравнения действительные, простые:
- Если дискриминант равен нулю (
= 0), то корни характеристического уравнения действительные, кратные:
- Если дискриминант меньше нуля (
где 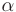
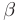
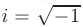
Теорема 7.3. Общее решение 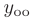
где 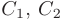
Пример:
Найти частные решения заданных линейных однородных дифференциальных уравнений второго порядка с постоянными коэффициентами, удовлетворяющие начальным условиям:
► Составим характеристическое уравнение, заменяя в дифференциальном уравнении производные неизвестной функции у соответствующими степенями неизвестного 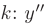
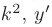
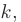
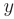
Дискриминант уравнения больше нуля:
В таком случае, корни характеристического уравнения действительные, простые:
Следовательно, общее решение дифференциального уравнения имеет вид
Частное решение получим из общего, используя для определения произвольных постоянных заданные начальные условия:
Решая полученную систему, находим значения произвольных постоянных:
После подстановки найденных значений в общее решение, искомое частное решение принимает вид
► Составим характеристическое уравнение:
Дискриминант уравнения равен нулю:
В таком случае, корни характеристического уравнения действительные, кратные:
Следовательно, общее решение дифференциального уравнения имеет вид
Найдем производную общего решения и определим произвольные постоянные из начальных условий:
Находим значения произвольных постоянных:
и подставим их в общее решение. Искомое частное решение принимает вид
Составим характеристическое уравнение:
Дискриминант меньше нуля:
В таком случае, корни характеристического уравнения комплексно-сопряженные:
Следовательно, общее решение дифференциального уравнения имеет вид
Используем для определения произвольных постоянных заданные начальные условия:
После подстановки найденных значений в общее решение, получим:
Этот материал взят со страницы заказа помощи по математике, там можно заказать помощь и ознакомиться с краткой теорией по предмету математика:
Возможно эти страницы вам будут полезны:




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Видео:Разностные уравнения | Решение задачСкачать

Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами
Видео:ЛОДУ 2 порядка c постоянными коэффициентамиСкачать

Основные понятия о линейных дифференциальных уравнениях второго порядка и их решениях
Линейным дифференциальным уравнением второго порядка называется уравнение вида
где y — функция, которую требуется найти, а p(x) , q(x) и f(x) — непрерывные функции на некотором интервале (a, b) .
Если правая часть уравнения равна нулю ( f(x) = 0 ), то уравнение называется линейным однородным уравнением. Таким уравнениям и будет в основном посвящена практическая часть этого урока. Если же правая часть уравнения не равна нулю ( f(x) ≠ 0 ), то уравнение называется линейным неоднородным уравнением (смотрите отдельный урок).
В задачах от нас требуется разрешить уравнение относительно y» :
Линейные дифференциальные уравнения второго порядка имеют единственное решение задачи Коши.
Видео:Уравнение в котором произведение множителей равно нулю. Алгебра 7 класс.Скачать

Линейное однородное дифференциальное уравнение второго порядка и его решение
Рассмотрим линейное однородное дифференциальное уравнение второго порядка:
Если y 1 (x) и y 2 (x) — частные решения этого уравнения, то верны следующие высказывания:
1) y 1 (x) + y 2 (x) — также является решением этого уравнения;
2) Cy 1 (x) , где C — произвольная постоянная (константа), также является решением этого уравнения.
Из этих двух высказываний следует, что функция
также является решением этого уравнения.
Возникает справедливый вопрос: не является ли это решение общим решением линейного однородного дифференциального уравнения второго порядка, то есть таким решением, в котором при различных значениях C 1 и C 2 можно получить все возможные решения уравнения?
Ответ на этот вопрос следуюший: может, но при некотором условии. Это условие о том, какими свойствами должны обладать частные решения y 1 (x) и y 2 (x) .
И это условие называется условием линейной независимости частных решений.
Теорема. Функция C 1 y 1 (x) + C 2 y 2 (x) является общим решением линейного однородного дифференциального уравнения второго порядка, если функции y 1 (x) и y 2 (x) линейно независимы.
Определение. Функции y 1 (x) и y 2 (x) называются линейно независимыми, если их отношение является константой, отличной от нуля:
Однако установить по определению, являются ли эти функции линейно независимыми, часто очень трудоёмко. Существует способ установления линейной независимости с помощью определителя Вронского W(x) :

Если определитель Вронского не равен нулю, то решения — линейно независимые. Если определитель Вронского равен нулю, то решения — линейно зависимымые.
Пример 1. Найти общее решение линейного однородного дифференциального уравнения 
Решение. Интегрируем дважды и, как легко заметить, чтобы разность второй производной функции и самой функции была равна нулю, решения должны быть связаны с экспонентой, производная которой равна ей самой. То есть частными решениями являются 

Так как определитель Вронского
не равен нулю, то эти решения линейно независимы. Следовательно, общее решение данного уравнения можно записать в виде

Видео:ЛОДУ с постоянными коэффициентами, корни характеристического уравнения | Лекция 37 | МатанализСкачать

Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами: теория и практика
Линейным однородным дифференциальным уравнением второго порядка с постоянными коэффициентами называется уравнение вида
где p и q — постоянные величины.
На то, что это уравнение второго порядка, указывает наличие второй производной от искомой функции, а на его однородность — нуль в правой части. Постоянными коэффициентами называются уже упомянутые выше величины.
Чтобы решить линейное однородное дифференциальное уравнение второго порядка с постоянными коэффициентами, нужно сначала решить так называемое характеристическое уравнение вида
которое, как видно, является обычным квадратным уравнением.
В зависимости от решения характеристического уравнения возможны три различных варианта решения линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами, которые сейчас разберём. Для полной определённости будем считать, что все частные решения прошли проверку определителем Вронского и он во всех случаях не равен нулю. Сомневающиеся, впрочем, могут проверить это самостоятельно.
Корни характеристического уравнения — действительные и различные
Иными словами, 

Пример 2. Решить линейное однородное дифференциальное уравнение

Решение. Характеристическое уравнение имеет вид 





Пример 3. Решить линейное однородное дифференциальное уравнение

Решение. Характеристическое уравнение имеет вид 





Корни характеристического уравения — вещественные и равные
То есть, 

Пример 4. Решить линейное однородное дифференциальное уравнение

Решение. Характеристическое уравнение 



Пример 5. Решить линейное однородное дифференциальное уравнение

Решение. Характеристическое уравнение 




Корни характеристического уравнения — комплексные
То есть, 



Пример 6. Решить линейное однородное дифференциальное уравнение

Решение. Характеристическое уравнение 





Пример 7. Решить линейное однородное дифференциальное уравнение

Решение. Характеристическое уравнение 





Решить линейное однородное дифференциальное уравнение с постоянными коэффициентами самостоятельно, а затем посмотреть решение
Пример 8. Решить линейное однородное дифференциальное уравнение

Пример 9. Решить линейное однородное дифференциальное уравнение

🔥 Видео
Как решать дробно-рациональные уравнения? | МатематикаСкачать

Задача Коши ➜ Частное решение линейного однородного дифференциального уравненияСкачать

Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентамиСкачать

Характеристическое уравнение в ДУСкачать

Решение однородного дифференциального уравнения. Практическая часть. 11 класс.Скачать

18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать

Решение линейного однородного дифференциального уравнения. Практическая часть. 11 класс.Скачать

Линейное однородное дифференциальное уравнение 2-го порядка с постоянными коэффициентами.Скачать

15. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентамиСкачать

Линейные однородные дифференциальные уравнения n-го порядка с постоянными коэффициентамСкачать

Видеоурок "Нахождение частных решений по виду правой части"Скачать

Решение тригонометрических уравнений. Подготовка к ЕГЭ | Математика TutorOnlineСкачать

ДОЭФ 2015. Лекция 0 (Дифференциальные уравнения)Скачать

2214 ЛНДУ. Правая часть - многочлен, среди корней характеристического уравнения нет нулей.Скачать

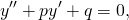
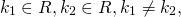
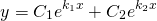
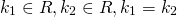
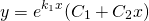
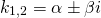
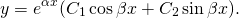
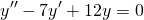
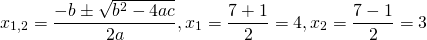
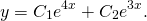
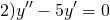
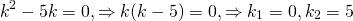
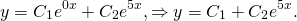
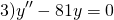
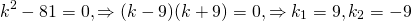
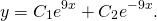
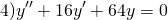
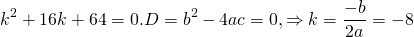
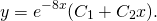
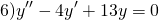
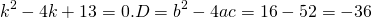
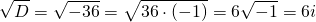
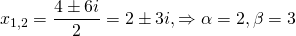
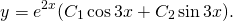
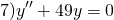
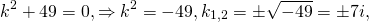
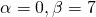
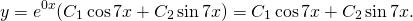

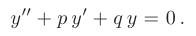
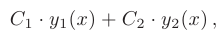
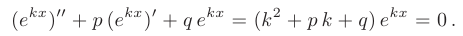
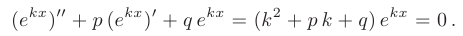
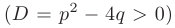 , то корни характеристического уравнения действительные, простые:
, то корни характеристического уравнения действительные, простые: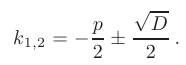
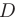 = 0), то корни характеристического уравнения действительные, кратные:
= 0), то корни характеристического уравнения действительные, кратные: