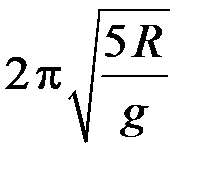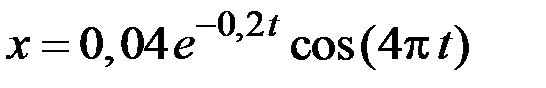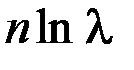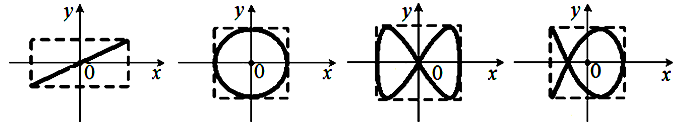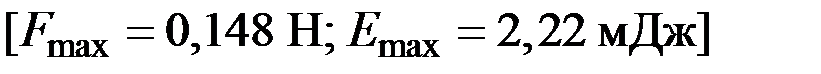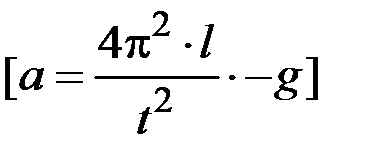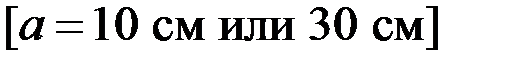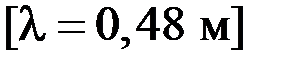Подготовка к ЕГЭ. Механические колебания.
Колебания – это движения или процессы, которые точно или приблизительно повторяются через определенные промежутки времени. Механические колебания — колебания механических величин.
( смещения, скорости, ускорения, энергии и т. д.)

Виды колебаний
 |
Автоколебания — колебания, возникающие под действием внутренних периодических сил ( при периодическом поступлении энергии от собственного источника внутри колебательной системы)
Условия возникновения свободных колебаний:
· Колебательная система должна иметь положение устойчивого равновесия.
· при выведении системы из положения равновесия должна возникать равнодействующая сила, возвращающая систему в исходное положение.
· Силы трения очень малы
Математический маятник – материальная точка, подвешенная на невесомой нерастяжимой нити.
Т = 2
Т = 2
Пружинный маятник – материальная точка, закрепленная на упругой пружине.
Гармонические колебания – колебания, при которых колеблющая величина изменяется со временем по закону синуса или косинуса.

Т хм – амплитуда – максимальное отклонение от
Т – период – время одного полного колебания
t, c ν – частота – число полных колебании за
1 2 единицу времени.
N – число колебании



ω – циклическая частота – число полных колебании за 2 π секунд.
φ = (ωt+φ0) – фаза – угловая физическая величина, показывающая положение и направление движения колебательной системы в данный момент времени.
φ0 – начальная фаза.
Уравнение гармонических колебании смещения колеблющей точки: Х = Хм S in (ωt+φ0);
Уравнение гармонических колебании скорости колеблющейся точки:
V = ХI = Хм ω Cos (ωt+φ0); где Vm = XM ω – амплитуда колебании скорости.
Ускорение колеблющейся точки:

Сила, действующая на колеблющееся тело равна F = m X ω2;
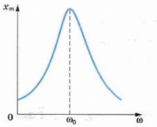
Резонанс – это явление, при котором резко возрастает
амплитуда вынужденных колебаний при совпадении собственной
частоты с частотой внешних периодических сил.
При колебательном движении тела происходит превращение кинетической энергии в потенциальную и обратно. При этом полная механическая энергия колеблющегося тела остается постоянной.

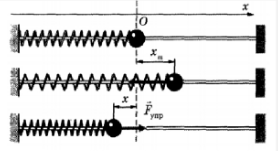
Точка О – положение равновесия. На рис. 1 тело находится в крайнем верхнем положении.

На рис.2 тело проходит положение равновесия. В точке О – скорость тела максимальна, а смещение равна 0. Полная механическая энергия равна.
: W =
На рис.3 (точка В) скорость тела равна 0, а смещение максимально. Поэтому полная механическая энергия равна: W =
На рис.4.(точка С) тело находится в промежуточном положении. В этой точке смещение равно Х и скорость тела равна V. Полная механическая энергия тела равна:
W =
И так за одно полное колебание тела превращение энергии из одного вида в другое происходит дважды.
Подготовка к ЕГЭ. Механические волны.
Волна – распространение колебаний от точки к точки( от частицы к частице) в пространстве( в упругой среде) с течением времени.
λ- длина волны- это кратчайшее расстояние между двумя ближайшими точками, колеблющимися в одинаково фазе. Это расстояние, на которое распространяется волна за один период.
Волновая поверхность – это геометрическое место точек среды, колеблющихся в одинаковых фазах.
Звук – продольная механическая волна, частота которых находится в пределах от 17Гц до 20кГц. Звук – акустические волны.
Если частота колебании меньше 17 Гц то колебания называются инфразвуком.
Колебания, частота колебании которых больше 20 кГц, называются инфразвуком.
Скорость звука в воздухе при 00С равна 331 м/с. Скорость звука зависит от среды и внешних условии. При увеличении температуры скорость звука увеличивается. Скорость звука в воде равна 1450м/с, в стали ≈ 5000 м/с.
Звук характеризуется высотой и громкостью. Высота звука определяется частотой: чем больше частота, тем выше звук. Громкость определяется амплитудой: чем больше амплитуда, тем громче звук.
Эхо – отраженная от препятствии звуковая волна. (от крутого берега, от опушки леса т. д.).
Звуковые волны могут вызвать вынужденные колебания в системах. При νзв = ν0 возникает резонанс.
Звук, соответствующий строго определенной частоте колебаний, называют музыкальным тоном. Наиболее чистый звук, соответствующий определенному тону, создают камертоны.
Шум – это звуковые волны всевозможных частот.

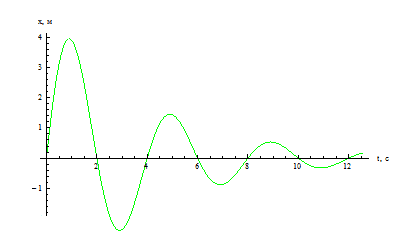
1.(1-07.Тр) На рисунке изображена зависимость 10
амплитуды установившихся колебаний маятника 8
от частоты вынуждающей силы (резонансная кривая). 6
Резонансная частота колебаний этого маятника равна 4
1) 0,5 Гц; 2) 1 Гц; 3) 1,5 Гц;Гц;

координаты тела от времени. Частота 3
равна 1) 0,12 Гц 2) 0,25 Гц 3) 0,5 Гц 1

Графики зависимости координаты
для двух тел. Отношение амплитуд
колебаний 
1) 

зависимости координаты от времени
для двух тел. Отношение периодов 2
колебаний 
1) 1; 2) 2; 3) 

5 Колебательное движение тела задано уравнением: х = a cos (bt + 
6 .Колебательное движение тела задано уравнением: х = a cos (bt + 


7 .Колебательное движение тела задано уравнением: х = a cos (bt + 

- Гармонические колебания
- теория по физике 🧲 колебания и волны
- Уравнение движения гармонических колебаний
- Период и частота гармонических колебаний
- Зависимость частоты и периода свободных колебаний от свойств системы
- Фаза колебаний
- Превращение энергии при гармонических колебаниях
- Резонанс
- Если колебание точки задано уравнением то период колебаний равен с
- Механические колебания и волны
- 🌟 Видео
Видео:Уравнения и графики механических гармонических колебаний. 11 класс.Скачать

Гармонические колебания
теория по физике 🧲 колебания и волны
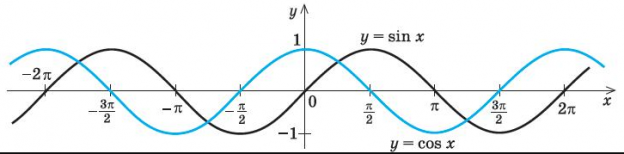
Гармоническими законами называют законы синуса и косинуса. Следовательно, гармоническими колебаниями называют те колебания, при которых координата тела изменяется синусоидально или косинусоидально.
Гармонические колебания — колебания, при которых координата тела изменяется с течением времени по гармоническому закону.
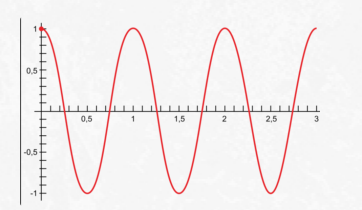
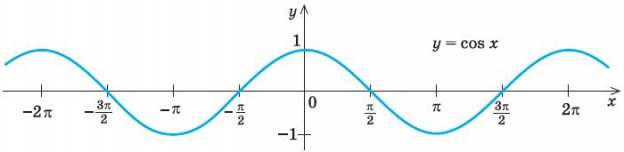
Ниже представлен график косинусоидальной функции. Обратите внимание, что косинус при возрастании аргумента от нуля сначала меняется медленно, а потом он все быстрее и быстрее приближается к нулю. Пройдя через него, его модуль снова быстро возрастает. Но по мере приближения к максимальному значению он снова замедляется. Точно так же меняются координаты свободно колеблющегося тела.
Важно! Гармоническими можно считать только те колебания, что совершаются грузом, закрепленном на пружине, или математическим маятником, отклоняемым на малый угол, при котором ускорение тела пропорционально его смещению.
Видео:МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ период колебаний частота колебанийСкачать

Уравнение движения гармонических колебаний
Известно, что ускорение колеблющегося на пружине груза пропорционально его смещению от положения равновесия:
Также известно, что ускорение есть вторая производная координаты. Следовательно, при свободных колебаниях координата изменяется со временем так, что вторая производная координаты по времени прямо пропорциональна самой координате и противоположна ей по знаку.
Вид — группа особей, сходных по морфолого-анатомическим, физиолого-экологическим, биохимическим и генетическим признакам, занимающих естественный ареал, способных свободно скрещиваться между собой и давать плодовитое потомство.
x″ = − x m a x cos . t = − x
Видно, что в этом случае теряется величина k m . . , служащая постоянной для каждой колебательной системы. Чтобы получить ее во второй производной, нужно усложнить функцию до следующего вида:
x = x m a x cos . √ k m . . t
Тогда первая производная примет
Вид — группа особей, сходных по морфолого-анатомическим, физиолого-экологическим, биохимическим и генетическим признакам, занимающих естественный ареал, способных свободно скрещиваться между собой и давать плодовитое потомство.
x′ = − √ k m . . x m a x sin . √ k m . . t
Вторая производная примет вид:
x″ = − k m . . x m a x cos . √ k m . . t = − k m . . x
Так как мы получили ровно такое же выражение, то описать свободные колебания можно уравнениями следующего вида:
x = x m a x sin . √ k m . . t
x = x m a x cos . √ k m . . t
Обозначим постоянную величину √ k m . . , зависящую от свойств системы, за ω0:
x = x m a x sin . ω 0 t
x = x m a x cos . ω 0 t
Само уравнение движения, описывающего свободные колебания, примет вид:
Видео:Выполнялка 53.Гармонические колебания.Скачать

Период и частота гармонических колебаний
Минимальный промежуток времени T, через который движение тела полностью повторяется, называют периодом колебания. Зная его, можно вычислить частоту колебаний, равную числу колебаний в единицу времени. Эти величины связаны между собой выражением:
Через промежуток времени, равный периоду T и соответствующий изменению аргумента косинуса на ω 0 T , движение тела повторяется, и косинус принимает прежнее значение. Но из математики известно, что наименьший период косинуса равен 2π. Следовательно:
ω 0 = 2 π T . . = 2 π ν
Таким образом, величина ω 0 представляет собой число колебаний тела, но не за 1 секунду, а за 2 π секунд. Эта величина называется циклической (круговой) частотой. А частоту свободных колебаний называют собственной частотой колебательной системы.
Видео:Уравнения и графики механических гармонических колебаний. Практ. часть - решение задачи. 11 класс.Скачать

Зависимость частоты и периода свободных колебаний от свойств системы
Изначально за величину ω 0 мы принимали постоянную, характеризующую свойства системы:
Теперь мы выяснили, что циклическая частота связана с периодом и частотой колебаний. Следовательно, период и частота колебаний также зависят от свойств системы:
ω 0 = √ k m . . = 2 π T . . = 2 π ν
Отсюда период и частота колебаний соответственно равны:
T = 2 π ω 0 . . = 2 π √ m k . .
ν = 1 2 π . . √ k m . .
Вспомним, что свойства колебательной системы математического маятника определяются постоянной величиной g l . . . Следовательно, циклическая частота для него равна:
Отсюда период и частота колебаний математического маятника соответственно равны:
T = 2 π ω 0 . . = 2 π √ l g . .
ν = 1 2 π . . √ g l . .
Эта формула была впервые получена и проверена на опыте голландским ученым Г. Гюйгенсом, современником И. Ньютона.
Период колебания возрастает с увеличением длины маятника. От массы маятника он не зависит. Это легко проверить на опыте с различными маятниками. Зависимость периода от ускорения свободного падения также легко прослеживается. Чем меньше величина g, тем больше период колебания маятника, и, следовательно, тем медленнее идут часы с маятником. Так, часы с маятником в виде груза на стержне отстанут в сутки почти на 3 с, если их поднять из подвала на верхний этаж Московского университета, который находится на высоте 200 м. И это только за счет уменьшения ускорения свободного падения с высотой.
Зависимость периода колебаний маятника от значения g используется на практике. Измеряя период колебания, можно легко измерить g. Ускорение свободного падения меняется с географической широтой. Но и на данной широте оно неодинаково, так как плотность земной коры неоднородна. В районах, где залегают более плотные породы, ускорение свободного падения принимает большие значения.
Пример №1. Сколько колебаний совершает математический маятник длиной 4,9 м за время 5 минут?
Искомое число колебаний равно отношению времени к периоду колебаний:
Период колебаний для математического маятника определяется формулой:
N = t 2 π . . √ g l . . = 300 2 · 3 , 14 . . √ 9 , 8 4 , 9 . . ≈ 68
Видео:Механические колебания. Как найти период колебаний? | ЕГЭ 2023 по физикеСкачать

Фаза колебаний
При заданной амплитуде гармонических колебаний координата колеблющегося тела в любой момент времени однозначно определяется аргументом косинуса или синуса, который равен ω 0 t . Обозначим его за ϕ и получим:
Величину ϕ, стоящую под знаком косинуса или синуса, называют фазой колебаний, описываемой этой функцией. Выражается фаза в угловых единицах — радианах (рад).
Фаза определяет значение не только координаты, но и других физических величин (к примеру, скорости и ускорения, которые также изменяются по гармоническому закону). Отсюда можно сделать вывод, что фаза определяет при заданной амплитуде состояния колебательной системы в любой момент времени.
Колебания с одинаковыми частотами и амплитудами могут отличаться друг от друга фазами. Так как ω 0 = 2 π T . . , фаза определяется формулой:
ϕ = ω 0 t = 2 π t T . .
t T . . — отношение, которое указывает, какая часть периода прошла от момента начала колебаний. Любому моменту времени, выраженному в долях периода, соответствует значение фазы, выраженное в радианах. К примеру:
| Время, t (с) | 0 | ||||||||||||||||||||||||||||||||||||||||||||
| Фаза, ϕ (рад) | 0 |
| –15 |
 |
 |
 |
| υ, см/с |
 , с , с |
5.13.На рисунке представлен график зависимости скорости колеблющейся материальной точки от времени. Уравнение колебаний имеет вид … ( 
1) 

4) 
5.14. Из графика колебаний материальной точки следует, что модуль скорости в момент времени t = 0,5 с равен … см/c.
1) 
5.15. Уравнение гармонических колебаний материальной точки 
1) 6,0 2) 4,0 3) 2,0 4) 1,0 5) 8,0
5.16. Материальная точка совершает механические колебания по закону 
1) 

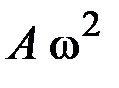

5.17.Середина струны колеблется с частотой 200 Гц и амплитудой 3 мм. Наибольшее ее ускорение равно … км/с 2 .
1) 0,12 2) 5,3 3) 4,7 4) 12 5) 6
5.18.Материальная точка совершает гармонические колебания. Если максимальное смещение и максимальная скорость точки составляют соответственно 10 см и 20 см/с, то ее максимальное ускорение равно … м/с 2 .
1) 4 2) 0,1 3) 0,2 4) 0,4 5) 2
5.19. На рисунках изображены зависимости от времени координаты и скорости материальной точки, колеблющейся по гармоническому закону. Циклическая частота колебаний равна … рад/с.
| t, с |
| 0,2 |
| 0,4 |
| 0,6 |
| 0,8 |
| 1,0 |
| 0,4 0,8 1,2 1,6 |
| х, м |
 ,м/с ,м/с |
| 1,0 |
| –2,0 |
| –1,0 |
| –1,5 |
| –0,5 |
| 0,2 0,6 1,0 1,4 1,8 |
| 0,5 |
| t, с |
| 1,5 |
| 2,0 |
1) 0,4 2) 0,8 3) 1 4) 1,5 5) 2
5.20. На рисунках изображены зависимости от времени координаты и ускорения материальной точки, колеблющейся по гармоническому закону. Циклическая частота колебаний равна … рад/с.
| t, с |
| –4 |
| –3 |
| –3,5 |
| –2,5 |
| –2 |
| 0,4 0,8 1,2 1,6 |
| а, м/с 2 |
| –1,5 |
| –1 |
| –0,5 |
| t, с |
| 0,2 |
| 0,4 |
| 0,6 |
| 0,8 |
| 1,0 |
| 0,4 0,8 1,2 1,6 |
| х, м |
1) 0,8 с -1 2) 1 с –1 3) 2 с –1 4) 3 с –1 5) 4 с –1
5.21.Уравнение движения материальной точки массой m = 10 г дано в виде 
1) 49 2) 0,12 3) 0,31 4) 0,49 5) 20
5.22.Материальная точка совершает гармонические колебания согласно уравнению 
1) 12 2) 15 3) 30 4) 40 5) 60
5.23. Материальная точка массой 

1) 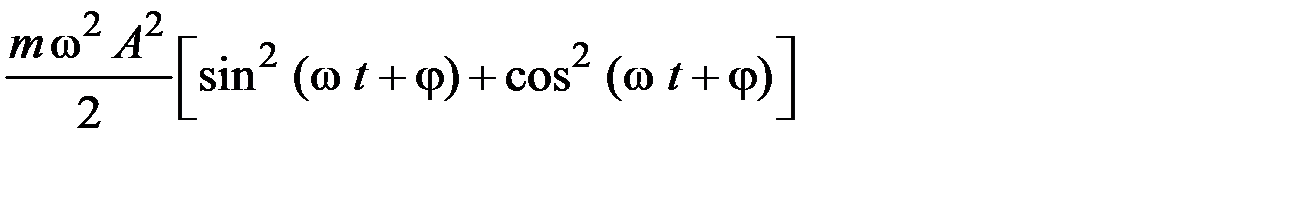
3) 

5.24.Материальная точка массой 

1) 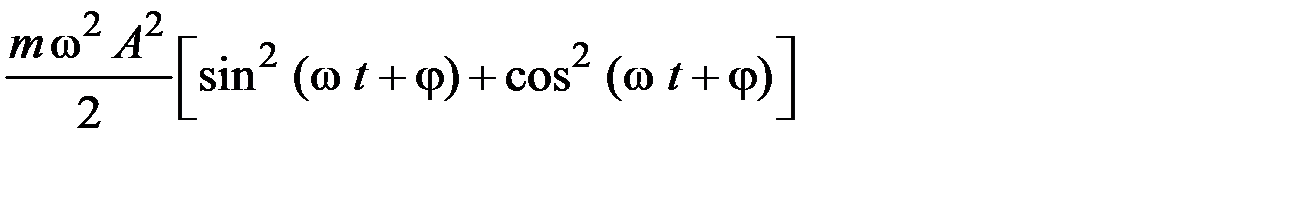
3) 

5.25.Математический маятник длиной 1 м установлен в лифте, опускающемся вниз с ускорением 2,5 м/с 2 . Период колебаний маятника равен … с.
1) 3,2 2) 1,6 3) 1,8 4) 2,0 5) 2,3
5.26. К пружине подвешен груз массой 10 кг. Если под влиянием силы 9,8 Н пружина растягивается на 1,5 см, то период вертикальных колебаний груза равен … с.
1) 2,58 2) 0,78 3) 0,96 4) 1,2 5) 1,8
5.27. Спиральная пружина обладает жесткостью k = 25 Н/м. Чтобы за время t = 1 мин совершалось 25 колебаний, к пружине надо подвесить груз массой … кг.
1) 0,001 2) 0,11 3) 1,66 4) 3,65 5) 9,55
5.28. Период колебаний физического маятника равен 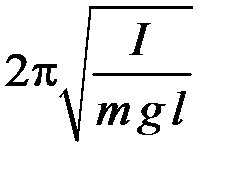
1) нет верного ответа
2) длина маятника
3) ширина маятника
4) длина оси маятника
5) расстояние от точки подвеса до центра масс
5.29. Математический маятник длиной l1 = 40 см и физический маятник в виде тонкого прямого стержня длиной l2 = 80 см и массой 0,5 кг синхронно колеблются около одной и той же горизонтальной оси. Приведенная длина физического маятника равна … см.
1) 2,72 2) 5,44 3) 80 4) 40 5) 32
5.30. Обруч диаметром D = 1 м, подвешенный на гвоздь, вбитый в стену, совершает малые колебания в плоскости, параллельной стене. Приведенная длина обруча равна … м.
1) 0,10 2) 2,0 3) 1,5 4) 1,0 5) 0,5
5.31.Тонкий обруч, подвешенный на гвоздь, вбитый горизонтально в стену, колеблется в плоскости, параллельной стене. Радиус обруча равен 30 см. Период колебаний равен … с.
1) 1 2) 1,1 3) 1,55 4) 1,8 5) 0,3
5.32.Диск радиусом R колеблется около горизонтальной оси, проходящей через одну из образующих цилиндрической поверхности диска. Период его колебаний равен …
1) 



5.33.Два диска с одинаковыми радиусами и с массами соответственно 2 и 8 кг совершают колебания относительно оси, касательной к их поверхности. Периоды колебаний дисков относятся как …
1) 4:1 2) 1:2 3) 1:1 4) 2:1 5) 1:4
5.34.Коэффициент затухания – это физическая величина, …
1) обратная времени, по истечении которого амплитуда колебаний уменьшается до нуля
2) показывающая, во сколько раз уменьшается амплитуда колебаний за период
3) обратная времени, по истечении которого амплитуда колебаний уменьшается в «е» раз
4) обратная числу колебаний, по завершению которых амплитуда колебаний уменьшается в «е» раз
5) обратная числу колебаний, по завершению которых амплитуда колебаний уменьшается до нуля
5.35.Коэффициент затухания колебаний маятника можно увеличить …
1) уменьшив начальную амплитуду колебаний и вязкость среды
2) уменьшив массу колеблющегося тела
3) уменьшив начальную амплитуду колебаний
4) увеличив массу колеблющегося тела
5) увеличив начальную амплитуду колебания
5.36. Шарик радиусом 10 см и массой 0,5 кг, подвешенный к нити длиной 20 см, совершает затухающие колебания в среде с коэффициентом затухания 2 кг·с –1 . Коэффициент сопротивления среды равен … с –1 .
1) 0,14 2) 1 3) 2 4) 4 5) 8
5.37. За 10 с амплитуда пружинного маятника массой m = 0,1 кг уменьшилась в е раз. Коэффициент затухания 

1) 
2) 
3) 
4) 
5) 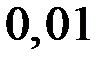
5.38. Период Т затухающих колебаний груза массой m на пружине жесткостью k можно рассчитать по формуле … ( 

1) 



5.39. За время релаксации амплитуда затухающих колебаний …
1) увеличивается в 2 раза
2) уменьшается в 2 раза
3) увеличивается в e раз
4) уменьшается в e раз
5) не изменяется
5.40.В момент времени t = 0 амплитуда затухающих колебаний маятника равна 4 см, период колебаний – 0,5 с, время релаксации – 5 с. Уравнение колебаний маятника имеет вид … м.
1)
2)
3)
4)
5.41. Логарифмический декремент затухания – это физическая величина, …
1) обратная промежутку времени, за которое амплитуда колебаний уменьшается до нуля
2) показывающая во сколько раз уменьшается амплитуда колебаний за период
3) обратная числу колебаний, по прошествии которых амплитуда колебаний уменьшается до нуля
4) обратная числу колебаний, по прошествии которых амплитуда колебаний уменьшается в «е» раз
5) обратная промежутку времени, за которое амплитуда колебаний уменьшается в «е» раз
5.42. Если период колебаний материальной точки – 2,5 с, коэффициент затухания – 2 с –1 , то логарифмический декремент затухания равен …
1) 0,8 2) 1,25 3) 5 4) 
5.43.За один период амплитуда колебаний математического маятника с логарифмическим декрементом затухания 
1) 0,3 2) 0,37 3) 1,35 4) 2,73 5) 3,33
5.44. Логарифмический декремент затухания колебаний маятника λ. Если амплитуда колебаний уменьшилась в n раз, то маятник совершил количество колебаний, равное …
1) 



5.45. Период затухающих колебаний системы Т = 4 с, логарифмический декремент затухания λ = 1,6. Добротность системы Q равна …
1) 6,4 2) 0,4 3) 0,79 4) 1,96 5) 2,5
5.46. Системе с наибольшей добротностью 
4) добротность во всех трех случаях одна и та же
5) ответ неоднозначен, так как результат зависит от амплитуды вынуждающей силы
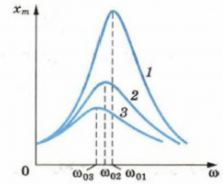
5.47. Пружинный маятник, частота собственных незатухающих колебаний которого ω0, совершает вынужденные колебания в вязкой среде под действием вынуждающей силы, изменяющейся по гармоническому закону с частотой ω. В процессе изменения этой частоты наблюдаются максимумы амплитуд смещения груза из положения равновесия при ω = ωх, скорости груза при ω = ωυ и его ускорения при ω = ωа. Полностью правильной последовательностью значений этих частот является…
1)
2)
3)
4)
5.48.При сложении двух одинаково направленных колебаний, описываемых уравнениями 

1) 

4) 
5.49. При сложении двух происходящих в одном направлении колебаний, описываемых соответственно уравнениями 

1) 0,34 2) 0,44 3) 0,58 4) 0,70 5) 0,80
5.50.Складываются два гармонических колебания одного направления с одинаковыми периодами и равными амплитудами 

1) 



5.51. Складываются два гармонических колебания одного направления с одинаковыми периодами. Результирующее колебание имеет максимальную амплитуду при разности фаз, равной …
1) 0 2) 


5.52.При сложении одинаково направленных гармонических колебаний одной частоты с амплитудами 10 см и 6 см возникло колебание с амплитудой 14 см. Разность фаз складываемых колебаний равна … градусов.
1) 120 2) 30 3) 45 4) 60 5) 90
5.53.Колебания с частотой 40 Гц распространяются в воздухе со скоростью 400 м/с. Соседние точки пространства, колебания в которых происходят в противофазе, находятся на расстоянии … м.
1) 400 2) 40 3) 20 4) 10 5) 5
5.54.В результате сложения двух гармонических колебаний одинакового направления получаются колебания с периодически изменяющейся амплитудой (биения). Период биений равен 0,25 с. Разность частот Δν складываемых колебаний равна … Гц.
1) 1 2) 2 3) 2,5 4) 4 5) 8π
5.55.В результате сложения двух гармонических колебаний одинакового направления с частотами 

1) 1 с 2) 1 мс 3) 10 мс 4) 50 мс 5) 0,5 с
5.56.При сложении двух гармонических колебаний одинакового направления с частотами 


1) 998 2) 1005 3) 1020 4) 1050 5) 1200
5.57. Материальная точка участвует в двух взаимно перпендикулярных колебаниях: 

1) прямая 2) эллипс 3) окружность 4) парабола
5.58. Материальная точка участвует в двух взаимно перпендикулярных колебаниях 

1) 

4) 
5.59. Материальная точка одновременно колеблется по гармоническому закону вдоль осей координат OX и OY с различными амплитудами, но одинаковыми частотами. При разности фаз, равной 
1) а 2) б 3) в 4) г
5.60. Материальная точка одновременно колеблется по гармоническому закону вдоль осей координат 0X и 0Y с одинаковыми амплитудами, с разностью фаз, равной 
1) а 2) б 3) в 4) г
5.61. Для продольной волны справедливо утверждение …
1) частицы среды колеблются в направлениях, перпендикулярных направлению распространения волны
2) возникновение волны связано с деформацией сдвига
3) частицы среды колеблются в направлении распространения волны
5.62.Уравнение бегущей вдоль оси х плоской гармонической волны имеет вид …
1) 

4) 
5.63.Уравнение плоской синусоидальной волны, распространяющейся вдоль оси ОХ, имеет вид 
1) 4 2) 6,28 3) 1 4) 1000 5) 0,01
5.64. Уравнение плоской синусоидальной волны, распространяющейся вдоль оси ОХ, имеет вид 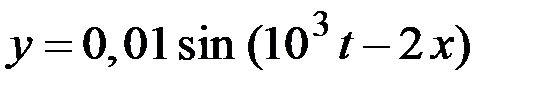
1) 2 2) 10 3) 100 4) 500 5) 1000
5.65. Период колебаний Т = 0,12 с. Колебания распространяются со скоростью υ = 300 м/с. Волновое число равно … м –1 .
1) 4·10 – 4 2) 0,17 3) 5,73 4) 36 5) 52
5.66.Уравнение плоской бегущей волны имеет вид у = 2 sin (4 t–3 x) м. Длина волны равна … см.
1) 209 2) 3 3) 75 4) 133 5) 157
5.67.Уравнение плоской синусоидальной волны, распространяющейся вдоль оси ОХ, имеет вид 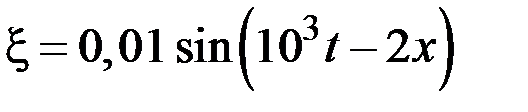
1) 2 2) 3,14 3) 500 4) 1000 5) 2000
5.68. Длина волны, распространяющейся в воздухе, равна 1 м. Разность фаз 
1) 0 2) 


5.69. Если расстояние между точками бегущей волны, распространяющейся в стали, равно 2,5 м, а колебания в них отличаются по фазе на 
1) 200 2) 500 3) 1000 4) 2500 5) 5000
5.70.Уравнение стоячей волны имеет вид …
1) 

4) 
5.71. Расстояние между соседними узлами стоячей волны, равно 10 см. Длина волны равна … м.
1) 0,05 2) 0,1 3) 0,15 4) 0,2 5) 0,4
5.72.Расстояние между пучностью и ближайшим к ней узлом стоячей волны равно 20 см. Длина волны равна … м.
1) 0,1 2) 0,2 3) 0,3 4) 0,4 5) 0,8
Задачи
5.73.Материальная точка массой 1 г совершает гармонические колебания. Амплитуда колебаний равна 5 см, циклическая частота 2 с –1 , начальная фаза равна 0. Определите силу, действующую на точку в тот момент, когда ее скорость равна 6 см/с.
5.74.Материальная точка массой m = 5 г совершает гармоническое колебание с частотой ν= 5 Гц. Амплитуда колебаний А = 3 см. Определите максимальную силу F, действующую на точку, и полную энергию Е колеблющейся точки.
5.75.Полная энергия тела, совершающего гармоническое колебательное движение, равна 30 мкДж, максимальная сила, действующая на тело – 1,5 мН. Чему равно смещение тела от положения равновесия через 1,25 периода колебаний, если в начальный момент оно составляло 2 см.
5.76.Для определения ускорения а, с которым поднимается вертикально вверх ракета, в нее был помещен математический маятник длиной l, который при взлете совершил N полных колебаний за время t. Найдите ускорение ракеты.
5.77.Математический маятник длиной 40 см и тонкий однородный стержень длиной 60 см совершают синхронные малые колебания вокруг горизонтальной оси. Найдите расстояние от центра стержня до этой оси.
5.78. Диск радиусом R = 24 см колеблется относительно оси, проходящей через середину одного из радиусов перпендикулярно плоскости диска. Определите период колебаний диска.
5.79.Уравнение колебаний физического маятника массой 0,2 кг и моментом инерции 0,4 кг·м 2 имеет вид 
5.80. На гвозде, вбитом в стену, в положении устойчивого равновесия висит квадратная рамка со стороной 20 см, сделанная из однородной тонкой проволоки. С каким периодом будут происходить её колебания после небольшого толчка?
5.81.Цилиндрический поплавок плавает в воде, погрузившись в нее на 4 см. Слегка надавив на поплавок, можно заставить его совершать колебания. С каким периодом они будут происходить? Сопротивлением воды пренебречь, ее плотность равна 1000 кг/м 3 .
5.82. Чему равен период колебаний деревянного кубика, плавающего в воде, если в равновесии он погружен в воду на 3/4. Плотность воды 10 3 кг/м 3 , длина ребра кубика – 10 см.
5.83.Начальная амплитуда затухающих колебаний маятника А0 = 3 см. Через t1 = 10 с амплитуда стала равной А1 = 1 см. Через какое время амплитуда станет равной А2 = 0,3 см.
5.84. Чему равен логарифмический декремент затухания математического маятника длиной 1 м, если за 1 минуту амплитуда колебаний уменьшилась в 2 раза?
5.85.Амплитуда затухающих колебаний маятника за время совершения 231 колебания уменьшилась вчетверо. Определите логарифмический декремент затухания.
5.86. Математический маятник совершает затухающие колебания. Логарифмический декремент затухания λ = 0,01. За время t = 100 с амплитуда колебаний уменьшилась в 10 раз. Найдите период затухающих колебаний.
5.87. К пружине подвесили груз, в результате чего она удлинилась на х = 9 см. Каков будет период колебаний Т груза, если его немного оттянуть вниз и затем отпустить? Логарифмический декремент затухания λ = 0,3.
5.88. Гиря массой 500 г подвешена к спиральной пружине жесткостью 20 Н/м и совершает затухающие колебания с логарифмическим декрементом 0,004. Сколько колебаний должна совершить гиря, чтобы амплитуда колебаний уменьшилась в два раза?
5.89.Сколько полных колебаний совершит гармонический осциллятор за время, в течение которого его энергияпосле начала колебаний уменьшится в 10 раз, если логарифмический декремент затухания λ = 0,03.
5.90. Тело массой m = 5 г совершает затухающие колебания. В течение времени t = 50 с тело потеряло 60% своей энергии. Определите коэффициент сопротивления r.
5.91.Найдите добротность математического маятника с длиной нити равной 20 см, у которого за 7 минут полная механическая энергия уменьшилась в 128 раз.
5.92.Складываются два гармонических колебания одного направления, описываемые уравнениями 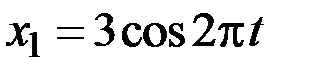

5.93.Поперечная волна распространяется вдоль упругого шнура со скоростью υ = 10 м/с. Амплитуда колебаний точек шнура А = 5 см, а период колебаний Т = 1 с. Запишите уравнение волны и определите:
1) длину волны; 2) фазу колебаний, смещение, скорость и ускорение точки, расположенной на расстоянии х1 = 9 м от источника колебаний в момент времени t = 2,5 с.
5.94. Уравнение незатухающих колебаний имеет вид 
5.95. Смещение от положения равновесия точки, находящейся от источника колебаний на расстоянии l = 4 см, в момент времени 
🌟 Видео
Урок 335. Анализ графика гармонических колебанийСкачать

Колебательное движение. Практическая часть - решение задачи. 9 класс.Скачать

Урок 329. Задачи на гармонические колебания - 1Скачать

Задание 23 из ОГЭ Построение графиков функций с модулем | МатематикаСкачать

Колебания математического и пружинного маятников. Практическая часть - решение задачи. 9 класс.Скачать

математический маятник ЕГЭ ФИЗИКА колебания частота периодСкачать

Урок 327. Гармонические колебанияСкачать

Задача на колебание грузика, прикрепленного к треугольнику. ВЫВОД ФОРМУЛЫ периода колебанийСкачать

Урок 92 (осн). Колебательное движение. МаятникиСкачать

Урок 353. Колебательный контурСкачать

Колебательное движение. Свободные колебания | Физика 9 класс #23 | ИнфоурокСкачать

















 Х хм – амплитуда колебаний точек
Х хм – амплитуда колебаний точек







 2)
2)  3)
3) 
 5)
5) 
 2)
2) 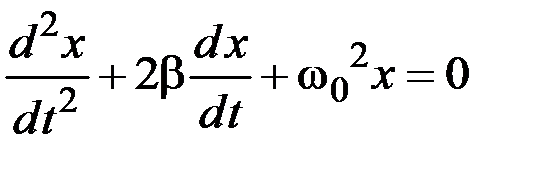
 4)
4) 

 2)
2) 
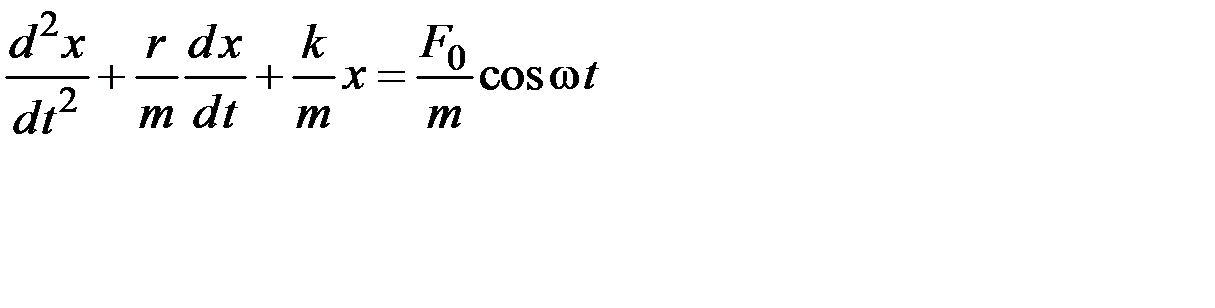
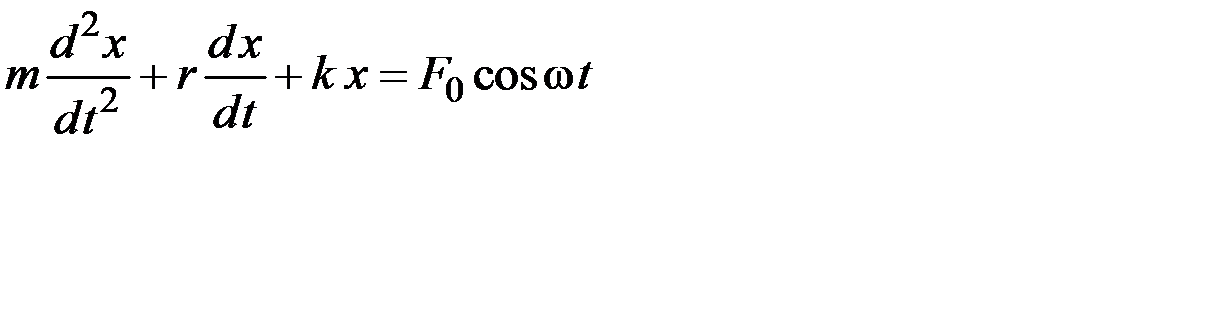
 2)
2)  3)
3) 
 5)
5) 
 . Начальная фаза колебаний равна … рад.
. Начальная фаза колебаний равна … рад. м. Период колебаний равен … с.
м. Период колебаний равен … с. . Период колебаний равен …, смещение по фазе колебаний координаты и ускорения равно …
. Период колебаний равен …, смещение по фазе колебаний координаты и ускорения равно … 2)
2)  3)
3) 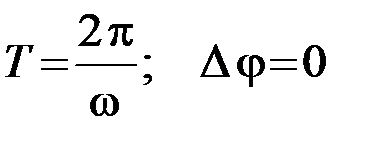
 5)
5) 
 м. Тело оказывается в точке с координатой
м. Тело оказывается в точке с координатой  через время … с.
через время … с. м. Длина маятника равна … м.
м. Длина маятника равна … м. м. Минимальный промежуток времени, через который после начала движения достигается максимальная скорость, равен … с.
м. Минимальный промежуток времени, через который после начала движения достигается максимальная скорость, равен … с. . Скорость точки будет равна половине ее максимальной скорости через долю периода Т, равную …
. Скорость точки будет равна половине ее максимальной скорости через долю периода Т, равную … 2)
2)  3)
3)  4)
4)  5)
5)