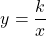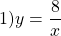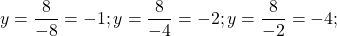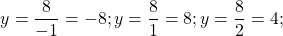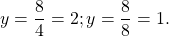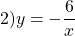Если k 0 в уравнении то ветви гиперболы расположены в (7 видео)

График обратной пропорциональности

График обратной пропорциональности — функции

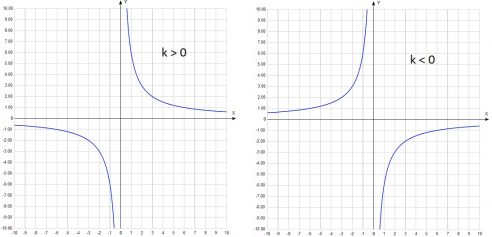
— гипербола. При k>0 ветви гиперболы расположены в I и III координатных четвертях, при k

Рассмотрим построение графика обратной пропорциональности на конкретных примерах.

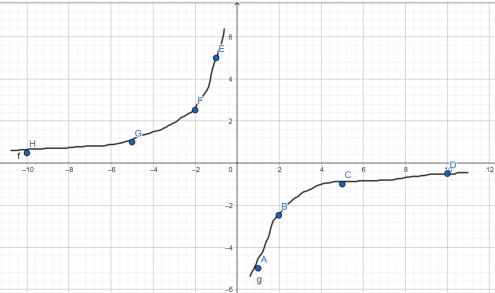
Эта функция — обратная пропорциональность. Её график — гипербола, ветви которой расположены в I и III координатных четвертях. Для построения гиперболы выберем значения x, на которые удобно делить 8: -8; -4; -2; -1; 1; 2; 4; 8. Подставляя их в формулу вместо x, находим соответствующие значения y:

Таким образом, нашли 8 точек с координатами

(-8;-1), (-4; -2), (-2; -4), (-1; -8), (1; 8), (2; 4), (4; 2) и (8; 1).

На практике эти вычисления оформляют в виде таблицы — в верхнюю строчку записывают выбранные значения x, в нижнюю — y, полученные при подстановке соответствующего значения x в формулу функции. Для функции y=8/x таблица выглядит так:

Полученные точки отмечаем на координатной плоскости:

Затем через эти точки проводим две ветви гиперболы:

Важно!

Оси Ox и Oy для гиперболы являются асимптотами. Это означает, что ветви гиперболы на бесконечности приближаются к осям, но никогда их не пересекут.

Для построения гиперболы можно брать только положительные значения x. Вторая ветвь гиперболы симметрична первой относительно точки O.

Эта функция — обратная пропорциональность. Её график — гипербола, ветви которой расположены во II и IV-й координатных четвертях. Для построения гиперболы составим таблицу:

Полученные точки отмечаем на координатной плоскости:

Содержание

Гипербола. График функции и свойства.
теория по математике 📈 функции
Свойства гиперболы (у= k x . )
Построение графика функции
Простейшие преобразования графиков функций.(10 класс)
Описание презентации по отдельным слайдам:
Краткое описание документа:
🎬 Видео

Видео:Видеоурок "Гипербола"Скачать

Гипербола. График функции и свойства.

теория по математике 📈 функции

Графиком функции у= k x . . , где k ≠ 0 число, а х – переменная, является кривая, которую называют гиперболой.

Гипербола имеет две ветви и может располагаться в 1 и 3 координатных четвертях, либо во 2 и 4. Это зависит от знака числа k. Рассмотрим данную кривую на рисунке, где показано ее расположение в зависимости от знака k.

Видео:Алгебра 8 класс (Урок№14 - Функция y = k/x и её график.)Скачать

Свойства гиперболы (у= k x . )

График функции симметричен относительно начала координат (0;0). Поэтому функцию еще называют – обратная пропорциональность.

Область определения – любое число, кроме нуля.
Область значения – любое число, кроме нуля.
Функция не имеет наибольших или наименьших значений.

Построение графика функции

Для построения графика функции необходимо подбирать несколько положительных и несколько отрицательных значений переменной х, затем подставлять их в заданную функцию для вычисления значений у. После этого по найденным координатам построить точки и соединить их плавной линией. Рассмотрим построение графиков на примерах.

Построить график функции у= 10 x . . .

Для этого построим две таблицы для положительных и отрицательных значений х. Подбирать желательно такие значения х, чтобы число 10 на них делилось

х	1	2	4	5	10
у

х	–1	–2	–4	–5	–10
у

Теперь делим на эти числа 10, получим значения у:

х	1	2	4	5	10
у	10	5	2,5	2	1

х	–1	–2	–4	–5	–10
у	–10	–5	–2,5	–2	–1

Выполняем построение точек, они будут располагаться в первой и третьей координатных четвертях, так как число k положительное.

Теперь для построения гиперболы соединим точки плавной линией. 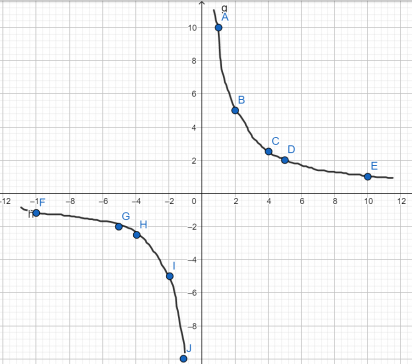Построить график функции у= − 5 x . . .

Для этого построим также две таблицы для положительных и отрицательных значений х. Подбирать желательно такие значения х, чтобы число минус 5 на них делилось. Выполняем деление и получаем значения у. При делении обращаем внимание на знаки, чтобы не допускать ошибок.

х	1	2	5	10
у	–5	–2,5	–1	–0,5

х	–1	–2	–5	–10
у	5	2,5	1	0,5

Теперь отмечаем точки во 2 и 4 координатных четвертях (число k отрицательное) и соединяем их для получения ветвей гиперболы.

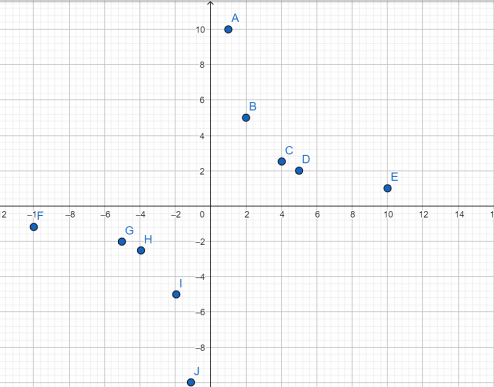
Установите соответствие между графиками функций и формулами, которые их задают.

1) y = x²

Для решения данной задачи необходимо знать

Вид — группа особей, сходных по морфолого-анатомическим, физиолого-экологическим, биохимическим и генетическим признакам, занимающих естественный ареал, способных свободно скрещиваться между собой и давать плодовитое потомство.

y = x² – парабола, в общем виде это y = ax²+bx+c, но в нашем случае b = c = 0, а а = 1

x/2 – прямая, в общем виде график прямой имеет вид y = ax + b, в нашем случае b = 0, а = 1/2

y = 2/x – гипербола, в общем виде график функции y = a/x + b, в данном примере b = 0, a = 2

Парабола изображена на рисунке А, гипербола на рисунке Б, а прямая – В.

pазбирался: Даниил Романович | обсудить разбор | оценить

Установите соответствие между функциями и их графиками.

В данной ситуации можно воспользоваться двумя подходами — можно руководствоваться общими соображениями, а можно просто решить задачу подстановкой. Я рекомендую решать задачу общими соображениями, а проверять подстановкой.

если уравнение гиперболы положительное (то есть не стоит знак -, как во втором и третьем случае), то график функции лежит в первой и третьей координатной четверти
если перед уравнением гиперболы стоит знак — (как в первом случае), то график лежит во второй и четвертой четвертях

Таким образом можно сразу определить, что первое уравнение соответствует графику под номером 2.

Второе правило, которым я пользуюсь, звучит так:

чем больше число в знаменателе гиперболы (рядом с x), тем сильнее гипербола жмется к осям координатной плоскости

чем больше число в числителе уравнения гиперболы, тем слабее и медленнее график функции прижимается к осям

Следовательно, функция Б слабее прижимается к осям и ей соответствует график 3, а функции В соответствует график 1, так как она сильнее прижимается к осям.

pазбирался: Даниил Романович | обсудить разбор | оценить

Видео:Гипербола. Функция k/x и её графикСкачать

Простейшие преобразования графиков функций.(10 класс)

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Рабочие листы и материалы для учителей и воспитателей

Более 300 дидактических материалов для школьного и домашнего обучения

Описание презентации по отдельным слайдам:

Простейшие преобразования графиков функций. класс: 10 Б Учитель математики: Розметова Б.Е Тема урока:

Цели урока: Научить учащихся преобразованию графика функции с использованием параллельного переноса, растяжения, сжатия вдоль оси координат, а также применению всех перечисленных видов для одной функции. Способствовать развитию наблюдательности, умения анализировать, преобразовывать графики данных функций, побуждать учеников к самоконтролю своей учебной деятельности, научить сравнивать, делать выводы, находить аналогию. Воспитать умение строить, преобразовывать графики линейной функции, квадратичной функции и обратной пропорциональности. Воспитать такие качества личности, как познавательная активность, самостоятельность.

Вопросы на повторение: Графиком линейной функции является _______________ . Графиком квадратичной функции является _______________ . Если в квадратичной функции , коэффициент а >0, то ветви параболы направлены _______________ . Если в квадратичной функции , коэффициент а 0, то парабола пересекает ось Ох в _______ точках. Если при решении D=0, то точка пересечения параболы и оси Ох является _____________ параболы. Если при решении квадратного уравнения D 0, либо в ______________ полуплоскости, если а 0 в уравнении , то ветви гиперболы расположены в _____ четверти и в _____ четверти. Если k 0 и в отрицательном направлении при d 1 растяжением в |k| раз вдоль оси Оу, а при 0 0.

IV. Растяжение и сжатие вдоль оси Ох. График функции y=f(аx) получаем из графика функции y=f(x) сжатием в |a| раз вдоль оси Ох при |a| > 1 и растяжением в раз вдоль оси Ох при |a|

Краткое описание документа:

Научить учащихся преобразованию графика функции с использованием параллельного переноса, растяжения, сжатия вдоль оси координат, а также применению всех перечисленных видов для одной функции. Способствовать развитию наблюдательности, умения анализировать, преобразовывать графики данных функций, побуждать учеников к самоконтролю своей учебной деятельности, научить сравнивать, делать выводы, находить аналогию. Воспитать умение строить, преобразовывать графики линейной функции, квадратичной функции и обратной пропорциональности. Воспитать такие качества личности, как познавательная активность, самостоятельность.