Если графики линейных уравнений пересекаются

Разделы: Математика

Цели урока:

1. Повторить знания школьников о линейной функции и ее графиках.
2. Рассмотреть взаимное расположение графиков линейных функций.
3. Продолжить развитие интереса к предмету.
4. Развивать умение анализировать и делать выводы.

Структура урока:

1. Организационный момент.
2. Актуализация опорных знаний.
3. Сообщение темы урока, цели урока.
4. Инструктирование и планирование работы.
5. Выполнение работы.
6. Подведение итогов.
7. Первичное закрепление, работа с учебником.
8. Постановка домашнего задания.

Подведение итогов урока.

Ход урока

1. Организационный момент.

Да, путь познания не гладок,
Но знаем мы со школьных лет,
Загадок больше,чем отгадок
И поискам предела нет.

2. Актуализация опорных знаний.

Подведение итога.

Сообщение темы урока, цели.

Инструктирование и планирование работы.

1. Каждому ученику выдаются планы исследовательской работы. (Приложение1)
2. Вы должны ответить на вопрос стоящий в начале.
3. Что для этого нужно сделать указано под цифрами 1 и 2.
4. На третий вопрос вам нужно ответить и сделать вывод, запись продолжить одним словом.
5. Вывод все записывают в тетрадь.
6. Три человека выполняют задание на больших листах и затем объясняют у доски это всему классу.
7. Все три вывода должны быть записаны всеми в тетради.

Выполнение работы.

Подведение итогов.

Первичное закрепление.

На доске ряд линейных функций. Не выполняя построения графиков, назовите пары функций, графики которых параллельны, пересекаются, перпендикулярны.

У=2х – 4, у=-4х + 2, у= 2х +3, у=2х, у= 7х – 8, у=5х +2.

Работа с учебником.

Прочитать вывод в учебнике с. 65, рассмотреть рисунки 31, 32.

Работа с учебником самостоятельно №335.

Постановка домашнего задания.

Домашнее задание дифференцированное.

• Оценка “3” — №337;
• оценка “4” ;
• “5” — №340.

Подведение итогов урока.

Видео:Решение системы линейных уравнений графическим методом. 7 класс.Скачать

Приложение 1

Как расположены графики двух линейных функций, если их угловые коэффициенты равны?

1. Составьте уравнение двух линейных функций так, чтобы их угловые коэффициенты были равны. Запишите полученные уравнения.
2. Постройте графики этих функций в одной системе координат (не забудьте подписать их).
3. Как располагаются относительно друга эти графики? Запишите вывод: если угловые коэффициенты двух линейных функций равны, то прямые, являющиеся их графиками. . .

Как расположены графики двух линейных функций, если их угловые коэффициенты не равны?

1. Составьте уравнение двух линейных функций так, чтобы их угловые коэффициенты были не равны. Запишите полученные уравнения.
2. Постройте графики этих функций в одной системе координат (не забудьте подписать их).
3. Как располагаются относительно друга эти графики? Запишите вывод: если угловые коэффициенты двух линейных функций не равны, то прямые, являющиеся их графиками. . .

Как расположены графики двух линейных функций, если произведение угловых коэффициентов равно (-1)?

1. Составьте уравнение двух линейных функций так, чтобы произведение их угловых коэффициентов было равно (-1). Запишите полученные уравнения.
2. Постройте графики этих функций в одной системе координат (не забудьте подписать их).
3. Как располагаются относительно друга эти графики? Запишите вывод: если угловые коэффициенты двух линейных функций в произведении дают (-1), то прямые, являющиеся их графиками. . .

На изучение темы “Линейная функция” отводится 9 часов. Данный урок является 6 в теме.

Видео:Линейная функция: краткие ответы на важные вопросы | Математика | TutorOnlineСкачать

График линейной функции, его свойства и формулы

О чем эта статья:

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Видео:Точки пересечения графика линейной функции с координатными осями. 7 класс.Скачать

Понятие функции

Функция — это зависимость «y» от «x», где «x» является переменной или аргументом функции, а «y» — зависимой переменной или значением функции.

Задать функцию значит определить правило, в соответствии с которым по значениям независимой переменной можно найти соответствующие ее значения. Вот, какими способами ее можно задать:

• Табличный способ — помогает быстро определить конкретные значения без дополнительных измерений или вычислений.
• Графический способ — наглядно.
• Аналитический способ — через формулы. Компактно, и можно посчитать функцию при произвольном значении аргумента из области определения.
• Словесный способ.

График функции — это объединение всех точек, когда вместо «x» можно подставить произвольные значения и найти координаты этих точек.

Видео:7 класс, 10 урок, Взаимное расположение графиков линейных функцийСкачать

Понятие линейной функции

Линейная функция — это функция вида y = kx + b, где х — независимая переменная, k, b — некоторые числа. При этом k — угловой коэффициент, b — свободный коэффициент.

Геометрический смысл коэффициента b — длина отрезка, который отсекает прямая по оси OY, считая от начала координат.

Геометрический смысл коэффициента k — угол наклона прямой к положительному направлению оси OX, считается против часовой стрелки.

Если известно конкретное значение х, можно вычислить соответствующее значение у.

Нам дана функция: у = 0,5х — 2. Значит:

• если х = 0, то у = -2;
• если х = 2, то у = -1;
• если х = 4, то у = 0;
• и т. д.

Для удобства результаты можно оформлять в виде таблицы:

Графиком линейной функции является прямая линия. Для его построения достаточно двух точек, координаты которых удовлетворяют уравнению функции.

Угловой коэффициент отвечает за угол наклона прямой, свободный коэффициент — за точку пересечения графика с осью ординат.

Буквенные множители «k» и «b» — это числовые коэффициенты функции. На их месте могут стоять любые числа: положительные, отрицательные или дроби.

Давайте потренируемся и определим для каждой функций, чему равны числовые коэффициенты «k» и «b».

Может показаться, что в функции «y = 0,2x» нет числового коэффициента «b», но это не так. В данном случае он равен нулю. Чтобы не поддаваться сомнениям, нужно запомнить: в каждой функции типа «y = kx + b» есть коэффициенты «k» и «b».

Еще не устали? Изучать математику веселее с опытным преподавателем на курсах по математике в Skysmart!

Видео:Точки пересечения графиков линейных функций. 7 класс.ОбразовательныйСкачать

Свойства линейной функции

1. Область определения функции — множество всех действительных чисел.
2. Множеством значений функции является множество всех действительных чисел.
3. График линейной функции — прямая. Для построения прямой достаточно знать две точки. Положение прямой на координатной плоскости зависит от значений коэффициентов k и b.
   
4. Функция не имеет ни наибольшего, ни наименьшего значений.
5. Четность и нечетность линейной функции зависят от значений коэффициентов k и b:
   b ≠ 0, k = 0, значит y = b — четная;
   b = 0, k ≠ 0, значит y = kx — нечетная;
   b ≠ 0, k ≠ 0, значит y = kx + b — функция общего вида;
   b = 0, k = 0, значит y = 0 — как четная, так и нечетная функция.
6. Свойством периодичности линейная функция не обладает, потому что ее спектр непрерывен.
7. График функции пересекает оси координат:
   ось абсцисс ОХ — в точке (-b/k, 0);
   ось ординат OY — в точке (0; b).
8. x=-b/k — является нулем функции.
9. Если b = 0 и k = 0, то функция y = 0 обращается в ноль при любом значении переменной х.
   Если b ≠ 0 и k = 0, то функция y = b не обращается в нуль ни при каких значениях переменной х.
10. Функция монотонно возрастает на области определения при k > 0 и монотонно убывает при k 0: функция принимает отрицательные значения на промежутке (-∞, — b /_k) и положительные значения на промежутке (- b /_k, +∞)
    При k b /_k, +∞) и положительные значения на промежутке (-∞, — b /_k).
11. Коэффициент k характеризует угол, который образует прямая с положительным направлением Ох. Поэтому k называют угловым коэффициентом.
    Если k > 0, то этот угол острый, если k

Видео:Линейная функция и её график. Алгебра, 7 классСкачать

Построение линейной функции

В геометрии есть аксиома: через любые две точки можно провести прямую и притом только одну. Исходя из этой аксиомы следует: чтобы построить график функции вида «у = kx + b», достаточно найти всего две точки. А для этого нужно определить два значения х, подставить их в уравнение функции и вычислить соответствующие значения y.

Например, чтобы построить график функции y = 1 /₃x + 2, можно взять х = 0 и х = 3, тогда ординаты этих точек будут равны у = 2 и у = 3. Получим точки А (0; 2) и В (3; 3). Соединим их и получим такой график:

В уравнении функции y = kx + b коэффициент k отвечает за наклон графика функции:

• если k > 0, то график наклонен вправо;
• если k 0, то график функции y = kx + b получается из y = kx со сдвигом на b единиц вверх вдоль оси OY;
• если b 1 /₂x + 3, y = x + 3.

Проанализируем рисунок. Все графики наклонены вправо, потому что во всех функциях коэффициент k больше нуля. Причем, чем больше значение k, тем круче идет прямая.

В каждой функции b = 3, поэтому все графики пересекают ось OY в точке (0; 3).

Теперь рассмотрим графики функций y = -2x + 3, y = — 1 /₂x + 3, y = -x + 3.

В этот раз во всех функциях коэффициент k меньше нуля, и графики функций наклонены влево. Чем больше k, тем круче идет прямая.

Коэффициент b равен трем, и графики также пересекают ось OY в точке (0; 3).

Рассмотрим графики функций y = 2x + 3, y = 2x, y = 2x — 2.

Теперь во всех уравнениях функций коэффициенты k равны. Получили три параллельные прямые.

При этом коэффициенты b различны, и эти графики пересекают ось OY в различных точках:

• график функции y = 2x + 3 (b = 3) пересекает ось OY в точке (0; 3);
• график функции y = 2x (b = 0) пересекает ось OY в точке начала координат (0; 0);
• график функции y = 2x — 2 (b = -2) пересекает ось OY в точке (0; -2).

Прямые будут параллельными тогда, когда у них совпадают угловые коэффициенты.

Подытожим. Если мы знаем знаки коэффициентов k и b, то можем представить, как выглядит график функции y = kx + b.

Если k 0, то график функции y = kx + b выглядит так:

0″ src=»https://user84060.clients-cdnnow.ru/uploads/5fc1049363f94987951092.png» style=»height: 600px;»>

Если k > 0 и b > 0, то график функции y = kx + b выглядит так:

0 и b > 0″ src=»https://user84060.clients-cdnnow.ru/uploads/5fc104b2640e6151326286.png» style=»height: 600px;»>

Точки пересечения графика функции y = kx + b с осями координат:

• С осью ОY. Абсцисса любой точки, которая принадлежит оси ОY равна нулю. Поэтому, чтобы найти точку пересечения с осью ОY, нужно в уравнение функции вместо х подставить ноль. Тогда получим y = b.
  Координаты точки пересечения с осью OY: (0; b).
• С осью ОХ. Ордината любой точки, которая принадлежит оси ОХ равна нулю. Поэтому, чтобы найти точку пересечения с осью ОХ, нужно в уравнение функции вместо y подставить ноль. И получим 0 = kx + b. Значит x = — b /_k.
  Координаты точки пересечения с осью OX: (- b /_k; 0)

Видео:ГРАФИК ЛИНЕЙНОГО УРАВНЕНИЯ С ДВУМЯ ПЕРЕМЕННЫМИ 7 КЛАСС видеоурокСкачать

Решение задач на линейную функцию

Чтобы решать задачи и строить графики линейных функций, нужно рассуждать и использовать свойства и правила выше. Давайте потренируемся!

Пример 1. Построить график функции y = kx + b, если известно, что он проходит через точку А (-3; 2) и параллелен прямой y = -4x.

• В уравнении функции y = kx + b два неизвестных параметра: k и b. Поэтому в тексте задачи нужно найти два условия, которые характеризуют график функции.
  Из того, что график функции y = kx + b параллелен прямой y = -4x, следует, что k = -4. То есть уравнение функции имеет вид y = -4x + b.
  Осталось найти b. Известно, что график функции y = -4x + b проходит через точку А (-3; 2). Подставим координаты точки в уравнение функции и мы получим верное равенство:
  2 = -4(-3) + b
  b = -10
• Таким образом, нам надо построить график функции y = -4x — 10
  Мы уже знаем точку А (-3; 2), возьмем точку B (0; -10).
  Поставим эти точки в координатной плоскости и соединим прямой:

Пример 2. Написать уравнение прямой, которая проходит через точки A (1; 1); B (2; 4).

1. Если прямая проходит через точки с заданными координатами, значит координаты точек удовлетворяют уравнению прямой y = kx + b.
   Следовательно, если координаты точек подставить в уравнение прямой, то получим верное равенство.
2. Подставим координаты каждой точки в уравнение y = kx + b и получим систему линейных уравнений.
3. Вычтем из второго уравнения системы первое, и получим k = 3.
   Подставим значение k в первое уравнение системы, и получим b = -2.

Видео:Построить график ЛИНЕЙНОЙ функции и найти:Скачать

Прямые на координатной плоскости

Линейная функция

График линейной функции

Прямые, параллельные оси ординат

Уравнения вида px + qy = r . Параллельные прямые. Перпендикулярные прямые

Видео:Линейная функция и ее график. 7 класс.Скачать

Линейная функция

Линейной функцией называют функцию, заданную формулой

где k и b – произвольные (вещественные) числа.

При любых значениях k и b графиком линейной функции является прямая линия .

Число k называют угловым коэффициентом прямой линии (1), а число b – свободным членом .

Видео:Точки пересечения графика линейной функции с координатными осями. Практическая часть. 7 класс.Скачать

График линейной функции

При k > 0 линейная функция (1) возрастает на всей числовой прямой, а её график ( прямая линия ) имеет вид, изображенный на рис. 1, 2 и 3.

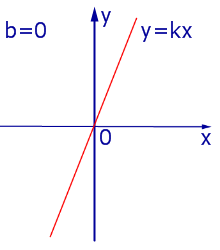Рис.1

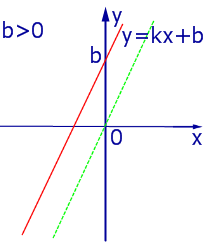Рис.2

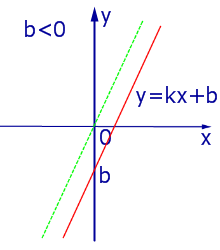Рис.3

При k = 0 линейная функция (1) принимает одно и тоже значение y = b при всех значениях x , а её график представляет собой прямую линию, параллельную оси абсцисс, и изображен на рис. 4, 5 и 6.

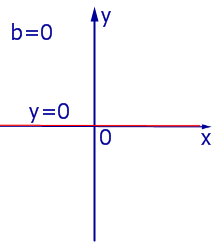Рис.4

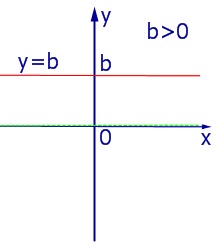Рис.5

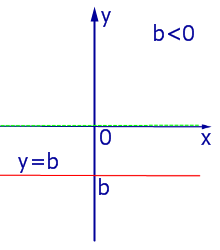Рис.6

При k линейная функция (1) убывает на всей числовой прямой, а её график ( прямая линия ) имеет вид, изображенный на рис. 7, 8 и 9.

k y = kx + b1 и y = kx + b2 , имеющие одинаковые угловые коэффициенты и разные свободные члены , параллельны . имеющие разные угловые коэффициенты , пересекаются при любых значениях свободных членов. y = kx + b1 и перпендикулярны при любых значениях свободных членов. Угловой коэффициент прямой линии y = kx (2) равен тангенсу угла φ , образованному (рис. 10) при повороте положительной полуоси абсцисс против часовой стрелки вокруг начала координат до прямой (2). Рис.10 Рис.11 Рис.12 Прямая (1) пересекает ось Oy в точке, ордината которой (рис. 11) равна b . При прямая (1) пересекает ось Ox в точке, абсцисса которой (рис. 12) вычисляется по формуле Видео:Занятие 1. График линейной функции y=kx+bСкачать Прямые, параллельные оси ординат Прямые, параллельные оси Oy , задаются формулой x = c , (3) где c – произвольное число, и изображены на рис. 13, 14, 15. Рис.13 Рис.14 Рис.15 Замечание 1 . Из рис. 13, 14, 15 вытекает, что зависимость, заданная формулой (3), функцией не является, поскольку значению аргумента x = c соответствует бесконечное множество значений y .; Видео:Как построить график линейной функции.Скачать Уравнение вида px + qy = r . Параллельные прямые. Перпендикулярные прямые px + qy = r , (4) где p, q, r – произвольные числа. В случае, когда уравнение (4) можно переписать в виде (1), откуда вытекает, что оно задаёт прямую линию . что и требовалось. В случае, когда получаем: откуда вытекает, что уравнение (4) задает прямую линию вида (3). В случае, когда q = 0, p = 0, уравнение (4) имеет вид 0 = r , (5) и при r = 0 его решением являются точки всей плоскости: В случае, когда уравнение (5) решений вообще не имеет. Замечание 2 . При любом значении r1 , не совпадающем с r прямая линия, заданная уравнением px + qy = r1 , (6) параллельна прямой, заданной уравнением (4) . Замечание 3 . При любом значении r2 прямая линия, заданная уравнением – qx + py = r2 , (7) перпендикулярна прямой, заданной уравнением (4) . Пример . Составить уравнение прямой, проходящей через точку с координатами (2; – 3) и параллельной к прямой 4x + 5y = 7 ; (8) перпендикулярной к прямой (8). В соответствии с формулой (6), будем искать уравнение прямой, параллельной прямой (8), в виде 4x + 5y = r1 , (9) где r1 – некоторое число. Поскольку прямая (9) проходит через точку с координатами (2; – 3), то справедливо равенство Итак, уравнение прямой, параллельной к прямой В соответствии с формулой (7), будем искать уравнение прямой, перпендикулярной прямой (8), в виде – 5x + 4y = r2 , (10) где r2 – некоторое число. Поскольку прямая (10) проходит через точку с координатами (2; – 3), то справедливо равенство 🎥 Видео Не выполняя построения графиков, найдите координаты точки пересечения прямых. Алгебра 7 класс.Скачать График линейного уравнения с двумя переменными. 6 класс.Скачать Как найти абсциссу точки пересечения двух прямых?Скачать Взаимное расположение прямых на плоскости. 7 класс.Скачать Урок ГРАФИК ЛИНЕЙНОЙ ФУНКЦИИ 7 КЛАСССкачать В какой четверти пересекаются графики. #ShortsСкачать Формула линейной функции по ее графикуСкачать Графики функций. Задание №11 | Математика ОГЭ 2023 | УмскулСкачать Поделиться или сохранить к себе: Смотрите также Сера — химические свойства, получение, соединения. Нитрат кальция: способы получения и химические свойства Кальций: способы получения и химические свойства Гидроксид натрия: способы получения и химические свойства Гидроксид кальция: способы получения и химические свойства Получение бензола Разница между глюкозой и сахарозой Гидроксид калия: способы получения и химические свойства