Если дано только 4 уравнения с 5 неизвестными (7 видео)

Математика

68. Уравнения с четырьмя и более неизвестными . Теперь ясны следующие соображения: одно уравнение с четырьмя неизвестными имеет бесконечно много решений, причем можно давать произвольные значения трем неизвестным, два уравнения с 4 неизвестными имеют бесконечно много решений, причем произвольные значения можно давать двум неизвестным, три уравнения с 4 неизвестными имеют бесконечно много решений, причем произвольные значения можно давать одному неизвестному, четыре уравнения с 4 неизвестными имеют лишь одно решение (конечно, если ни одно из этих уравнений не есть следствие остальных и не противоречит остальным).

Такие соображения можно продолжить и дальше. Например, 5 уравнений с 8-ю неизвестными имеют бесконечно много решений, причем произвольные значения можно давать трем неизвестным и т. п.

Решать системы уравнений с большим числом неизвестных приходится редко. Следует при этом решении пользоваться по возможности всеми особенностями уравнений, чтобы упростить решение.

Рассмотрим 2 примера. Пример 1:

x + y + 2z – t = 9
x + y – 2z + t = 7
x – y + z + 2t = –9
x – y – z – 2t = 5

Сложив 1-е и 2-е уравнения по частям, мы получим очень простое уравнение только с двумя неизвестными, а именно

2x + 2y = 16 или x + y = 8.

Сложив по частям 3-е и 4-е уравнения, получим:

2x – 2y = –4 или x – y = –2.

Теперь легко решить 2 полученных уравнения (x + y = 8 и x – y = –2), и тогда найдем x = 3 и y = 5.

Подставляя эти значения в 1-е и в 3-е уравнения, получим:

3 + 5 + 2z – t = 9 или 2z – t = 1
3 – 5 + z + 2t = –9 или z + 2t = –7

Подстановка этих значений во 2-е и 4-е уравнения приведет к таким же точно уравнениям.

Теперь остается решить 2 уравнения с 2 неизвестными:

Содержание

Метод Гаусса онлайн
Предупреждение
Метод Гаусса
Примеры решения системы линейных уравнений методом Гаусса
Если дано только 4 уравнения с 5 неизвестными
Контакты
💡 Видео

Видео:Система с тремя переменнымиСкачать

Метод Гаусса онлайн

Данный онлайн калькулятор находит решение системы линейных уравнений (СЛУ) методом Гаусса. Дается подробное решение. Для вычисления выбирайте количество переменных и количество уравнений. Затем введите данные в ячейки и нажимайте на кнопку «Вычислить.»

Предупреждение

Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.

Видео:Решение простых уравнений. Что значит решить уравнение? Как проверить решение уравнения?Скачать

Метод Гаусса

Метод Гаусса − это метод перехода от исходной системы линейных уравнений (при помощи эквивалентных преобразований) к системе, которая решается проще, чем исходная система.

Эквивалентными преобразованиями системы линейных уравнений являются:

перемена местами двух уравнений в системе,
умножение какого-либо уравнения в системе на ненулевое действительное число,
прибавление к одному уравнению другого уравнения, умноженного на произвольное число.

Рассмотрим систему линейных уравнений:

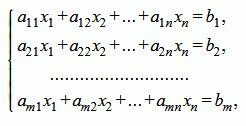Если дано только 4 уравнения с 5 неизвестными

(1)

Запишем систему (1) в матричном виде:

Ax=b

(2)

(3)

A-называется матрица коэффициентов системы, b − правая часть ограничений, x− вектор переменных, которую нужно найти. Пусть rang(A)=p.

Эквивалентные преобразования не меняют ранг матрицы коэффициентов и ранг расширеннной матрицы системы. Не меняется также множество решений системы при эквивалентных преобразованиях. Суть метода Гаусса заключается в приведении матрцы коэффициентов A к диагональному или ступенчатому.

Построим расшренную матрицу системы:

(4)

Предположим a₁₁≠0. Если это не так, то можно поменять местами эту строку со строкой с ненулевым элементом в столбце 1 (если нет таких строк, то переходим к следующему столбцу). Обнуляем все элементы столбца 1 ниже ведущего элемента a₁₁. Для этого сложим строки 2,3, . m со строкой 1, умноженной на −a₂₁/a₁₁, −a₃₁/a₁₁, . −a_m1/a₁₁, соответственно. Тогда (4) примет следующий вид:

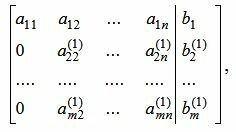(5)

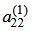
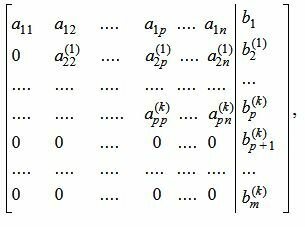На следующем этапе обнуляем все элементы столбца 2, ниже элемента . Если данный элемент нулевой, то эту строку меняем местами со строкой, лежащий ниже данной строки и имеющий ненулевой элемент во втором столбце. Далее обнуляем все элементы столбца 2 ниже ведущего элемента a₂₂. Для этого сложим строки 3, . m со строкой 2, умноженной на −a₃₂/a₂₂, . −a_m2/a₂₂, соответственно. Продолжая процедуру, получим матрицу диагонального или ступенчатого вида. Пусть полученная расширенная матрица имеет вид:

(6)

Обратим внимание на последние строки. Если 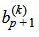. равны нулю, то система линейных уравнений имеет решение, если же хотя бы один из этих чисел отлично от нуля, то система несовместна. Иными словами, система (2) совместна тогда и только тогда, когда ранг матрицы A навен рангу расширенной матрицы (A|b).

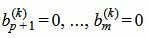
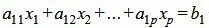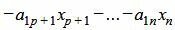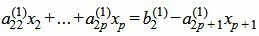Пусть . Тогда

(7)

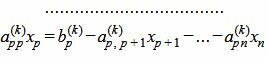Так как rangA=rang(A|b), то множество решений (7) есть (n−p)− многообразие. Следовательно n−p неизвестных можно выбрать произвольно. Остальные неизвестные из системы (7) вычисляются так. Из последнего уравнения выражаем x_p через остальные переменные и вставляем в предыдущие выражения. Далее из предпоследнего уравнения выражаем x_p−1 через остальные переменные и вставляем в предыдущие выражения и т.д. Рассмотрим метод Гаусса на конкретных примерах.

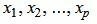
Видео:Математика без Ху!ни. Метод Гаусса. Совместность системы. Ранг матрицы.Скачать

Примеры решения системы линейных уравнений методом Гаусса

Пример 1. Найти общее решение системы линейных уравнений методом Гаусса:

Матричный вид записи: Ax=b, где

Для решения системы, запишем расширенную матрицу:

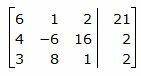Обозначим через a_ij элементы i-ой строки и j-ого столбца.

Исключим элементы 1-го столбца матрицы ниже элемента a_{1 1}. Для этого сложим строки 2,3 со строкой 1, умноженной на -2/3,-1/2 соответственно:

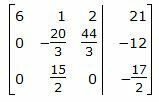Исключим элементы 2-го столбца матрицы ниже элемента a2 2. Для этого сложим строку 3 со строкой 2, умноженной на 9/8:

Делим каждую строку матрицы на соответствующий ведущий элемент (если ведущий элемент существует):

Из вышеизложенной таблицы можно записать:

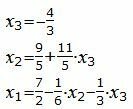Подставив верхние выражения в нижние, получим решение.

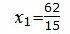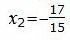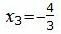Пример 2. Найти общее решение системы линейных уравнений методом Гаусса:

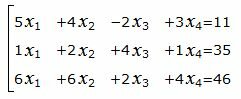Матричный вид записи: Ax=b, где

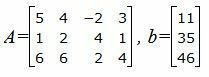Для решения системы, построим расширенную матрицу:

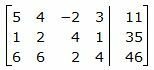Обозначим через a_ij элементы i-ой строки и j-ого столбца.

Исключим элементы 1-го столбца матрицы ниже элемента a₁₁. Для этого сложим строки 2,3 со строкой 1, умноженной на -1/5,-6/5 соответственно:

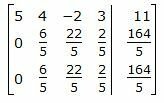Исключим элементы 2-го столбца матрицы ниже элемента a₂₂. Для этого сложим строку 3 со строкой 2, умноженной на -1:

Делим каждую строку матрицы на соответствующий ведущий элемент (если ведущий элемент существует):

Выразим переменные x₁, x₂ относительно остальных переменных.

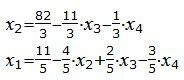где x₃, x₄− произвольные действительные числа.

Подставив верхние выражения в нижние, получим решение.

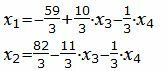где x₃, x₄− произвольные действительные числа.

Векторный вариант решения:

Запишем вышеизложенное решение, представив свободные переменные в виде тождеств:

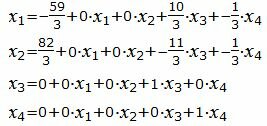Тогда векторное решение можно представить так:

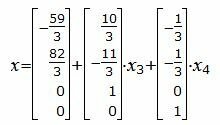где x₃, x₄− произвольные действительные числа.

Видео:Решение уравнений в несколько действий. Как объяснить ребенку решение уравнений?Скачать

Если дано только 4 уравнения с 5 неизвестными

Запрошуємо усіх хто любить цікаві задачі та головоломки відвідати групу! Зараз діє акція — підтримай студента! Знижки на роботи + безкоштовні консультації.