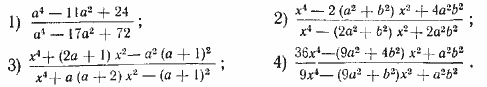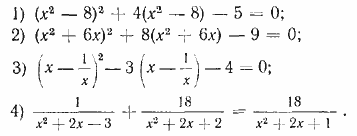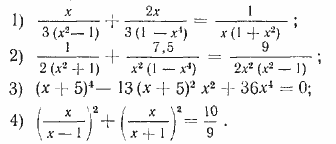3 ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА. КВАДРАТНЫЕ УРАВНЕНИЯ
§ 8. БИКВАДРАТНЫЕ УРАВНЕНИЯ
Решить биквадратные уравнения:
458. 1) х 4 + х 2 — 2 = 0;
2) х 4 — 3х 2 — 4 = 0;
3) 9х 4 + 8х 2 — 1 = 0;
4) 20х 4 — х 2 — 1 = 0.
459. 1) х 4 — 26х 2 + 25 = 0;
2) х 4 — 40х 2 + 144 = 0;
3) 4х 4 — 5х 2 + 1 = 0;
4) 4х 4 — 17х 2 + 4 = 0.
460. 1) х 4 — 18х 2 + 81=0;
2) 256х 4 — 32х 2 +1=0;
3) х 4 — 8х 2 + 20 = 0;
4) 5х 4 — 4х 2 + 1 = 0.
462. Убедиться, что уравнение х 4 + 10х 2 + 9 = 0 не имеет действительных корней. Почему этот вывод можно сделать, не решая уравнения?
463. Дано биквадратное уравнение ах 4 + bх 2 + с = 0, где а, b, с—данные действительные числа, причем а > 0. Введя вспомогательное неизвестное у = х 2 , исследовать корни данного уравнения и результаты исследования занести в таблицу 4.
464. Решить уравнения:
465. Почему биквадратное уравнение, имеющее корень, равный т, имеет также и второй корень, равный — т?
466. Один из корней биквадратного уравнения равен 2, а другой корень 2√ 2 . Составить уравнение.
* 467. Составить биквадратное уравнение, сумма квадратов корней которого равна 26, а произведение корней равно 36.
468. Разложить на множители:
469. Сократить дроби:
470. Решить уравнения посредством введения вспомогательного неизвестного:
471. Решить уравнения выделением из левой части полного квадрата:
1) х 4 — 20х 2 + 64 = 0;
2) х 4 — 13х 2 + 36 = 0;
3) х 4 — 4х 2 + 1 = 0;
4) х 4 — 2х 2 +1 = 0.
472*. Зная, что т и п— корни уравнения х 2 + рх + q = 0, найти биквадратное уравнение, имеющее корни —т, —п, т и п.
473. Решить уравнения:
474*. В какой системе счисления число 100 запишется в виде 10 201?
475. Сумма площадей двух квадратов равна 4,25 дм 2 . Найти коэффициенты подобия этих квадратов, если известно, что их стороны выражаются взаимно обратными числами.
476. Каким радиусом следует описать дугу с центром на окружности, радиус которой R, чтобы расстояние между точками пересечения этой дуги с данной окружностью было равно а, где а 3 ; R√ 2 и R.
Видео:Решение биквадратных уравнений. 8 класс.Скачать
Биквадратное уравнение
Уравнение которое выглядит как ax 4 +bx 2 +c=0, называют Биквадратным уравнением. В нем х — неизвестная переменная. a,b,c -имеют различное числовое значение, где, а не равно нулю. Так же при х — стоящем в четвертой степени, коэффициент а — называется старшим, и х — стоящем во -второй степени, коэффициент b — называется вторым, с — является свободным членом.
Корнем биквадратного уравнения является значение х если при его использовании уравнение ax 4 +bx 2 +c превращается в ноль.
Действие с помощью которого находятся все корни уравнения или выясняется что таковых у него нет, называется — решением биквадратного уравнения.
Для решения биквадратного уравнения существует ряд действий, которые следует придерживаться.
Во-первых: Путем подстановки, где у=х 2 , решаемое биквадратное уравнение переводим в квадратное ау 2 +bу+с=0.
Во-вторых: В полученном уравнении необходимо найти корни.
В-третьих: Произвести замену введенного нами значения х 2 , путем приравнивания получившихся корней квадратного уравнения.
В- четвертых: После решения полученного уравнения, находим корни в биквадратном уравнении.
Для того чтобы все легче усвоилось, рассмотрим все описанное на нескольких примерах.
1) Дано уравнение 2х 4 -19х 2 +9=0, оно биквадратное.
Производим замену х 2 =у, следовательно, х 4 =у 2 ,
записываем получившееся 2у 2 -19у+9=0,
Мы получили полное неприведенное уравнение с коэффициентами а=2, b=-19,с=9.
Дискриминант уравнения: D = b 2 — 4ac= (-19) 2 — 4 * 2 * 9 = 361 — 72 = 289
У квадратного уравнения 2 корня, потому как D=289, что больше ноля. Находим их.
у1 = (-b+ √D)/2a = (-(-19)+ √289)/(2*2) = (19+17)/4 = 36/4 = 9
y2 = (-b- √D)/2a =(-(-19)±√289)/(2*2) = (19-17)/4 = 2/4 = 1/2
Производим замену х1 =у1, и х2 =у2
Данное биквадратное уравнение имеет ответ: х1 = 3; х2 =-3; х3 = 1/√2; х4= — 1/√2 .
2) Рассмотрим уравнение х 4 +2х2-8=0
Производим замену х 2 =у, следовательно, х 4 =у 2 ,
записываем получившееся у 2 +2у-8=0,
Мы получили полное неприведенное уравнение с коэффициентами а=1, b=2,с=-8.
Дискриминант уравнения: D = b 2 — 4ac=22 — 4 * 1 *(-8) = 4 + 32 = 36
У квадратного уравнения 2 корня, потому как D=36, что больше ноля. Находим их.
у1 = (-b+ √D)/2a = (-2+ √36)/(2*1) = (-2+6)/2 = 4/2 = 2
y2 = (-b- √D)/2a =(-2 — √36)/(2*1) = (-2-6)/2 = (-8)/2 = -4
Производим замену х2 =у1, и х2 =у2
х1=2
х1,2= +√2
х3 = 4 (решения нет)
Данное биквадратное уравнение имеет ответ: х1 =√2; х2 = -√2
Из данного уравнения мы можем сделать вывод. Если при решении получается корень со знаком минус или у меньше ноля, больше его не рассматриваем. т.к. он не подходит нам по условию.
Для приведения многочлена к стандартному виду, во многих случаях используют формулы сокращенного умножения. Они решаются с помощью открытия скобок.
Видео:Как разобраться в корнях ? Квадратный корень 8 класс | Математика TutorOnlineСкачать
Биквадратные уравнения
теория по математике 📈 уравнения
Уравнение вида ax 4 +bx 2 +c=0, где а≠0 число, называется биквадратным уравнением (приставка «би» означает «двойной»). Для решения такого уравнения применяют метод введения новой переменной, чтобы получить квадратное уравнение, решение которого легко выполняется.
Рассмотрим на примерах решение таких уравнений.
Пример №1. Решить уравнение:
В данном уравнении заменим х 2 на переменную, например а (букву для замены можно брать любую): х 2 =а. Степень данного уравнения при этом понизится на 2, получаем квадратное уравнение:
Решаем данное уравнение, например, по теореме Виета. Тогда:
Методом подбора получаем корни квадратного уравнения 9 и 16. Проверяем, что действительно 9+16=25, 916=144. Теперь переходим к нахождению корней биквадратного уравнения, которое дано по условию. Мы заменяли х 2 на а, поэтому подставляем вместо а полученные значения – это 9 и 16:
Теперь находим корни каждого из этих неполных квадратных уравнений: х 2 =9, отсюда уравнение имеет два корня ±3; х 2 =16, отсюда имеет еще два корня ±4. Следовательно, данное биквадратное уравнение имеет четыре корня: 3, -3, 4, -4.
Пример №2. Решить уравнение:
Заменим на переменную у: х 2 =у. Получим уравнение:
Найдем его корни: у1=–1, у2=4. Подставим корни вместо у и получим уравнения: х 2 =–1; х 2 =4. Видим, что первое неполное квадратное уравнение не имеет корней, а корни второго уравнения – это ±2. Значит, данное биквадратное уравнение имеет корни ±2.
Пример №3. Решить уравнение:
Выполним замену переменной: х 2 =у. Решим уравнение:
Подбором корни найти невозможно, поэтому через дискриминант получаем, что корней нет, так как дискриминант будет отрицательный. Значит и данное биквадратное уравнение тоже не имеет корней.
Видео:Как решать любое квадратное уравнение Полное Неполное квадр ур x^2+2x-3=0 5x^2-2x=0 2x^2-2=0 3x^2=0Скачать
Биквадратные уравнения
Биквадратное уравнение — уравнение, которое можно привести к виду:
Для решения биквадратных уравнений x 2 заменяется на любую другую букву, например, на y, то есть:
Следовательно, относительно y, уравнение является квадратным и решается по формуле корней квадратного уравнения, а затем вычисляются корни биквадратного уравнения, если они есть.
Пример. Решить уравнение:
Решение: Заменяем x 2 на y, чтобы получить квадратное уравнение:
D = b 2 — 4ac = (-10) 2 — 4 · 1 · 9 = 100 — 36 = 64, D > 0.
📺 Видео
5 способов решения квадратного уравнения ➜ Как решать квадратные уравнения?Скачать
Решение квадратных уравнений. Дискриминант. 8 класс.Скачать
Быстрый способ решения квадратного уравненияСкачать
Как решить квадратное уравнение за 30 секунд#математика #алгебра #уравнение #дискриминант #репетиторСкачать
БИКВАДРАТНОЕ УРАВНЕНИЕ В ЕГЭ #shorts #математика #егэ2022 #огэ2021 #уравнениеСкачать
Неполные квадратные уравнения. Алгебра, 8 классСкачать
РАЗБИРАЕМ ДИСКРИМИНАНТ ЧАСТЬ I #shorts #математика #егэ #огэ #дискриминантСкачать
Формула корней квадратного уравнения. Алгебра, 8 классСкачать
Квадратные уравнения от «А» до «Я». Классификация, решение и теорема Виета | МатематикаСкачать
8 класс. Квадратное уравнение и его корни. Алгебра.Скачать
Квадратное уравнение. Как решить? | Математика ОГЭ 2023 | УмскулСкачать
5 Лайфхаков Которые Помогут Решить Биквадратное УравнениеСкачать
Биквадратное уравнениеСкачать
Ещё один способ решения квадратных уравненийСкачать
5. ПРИ КАКИХ ЗНАЧЕНИЯХ ПАРАМЕТРА УРАВНЕНИЕ ИМЕЕТ КОРЕНЬ, РАВНЫЙ ЧИСЛУ ... ?Скачать
САМЫЙ ПРОСТОЙ СПОСОБ ПОНЯТЬ ТЕОРЕМУ ВИЕТА #shorts #математика #егэ #огэ #теорема #теоремавиетаСкачать
Решаем квадратные уравнения в уме! 🤯Скачать
