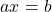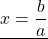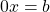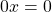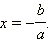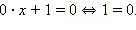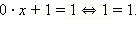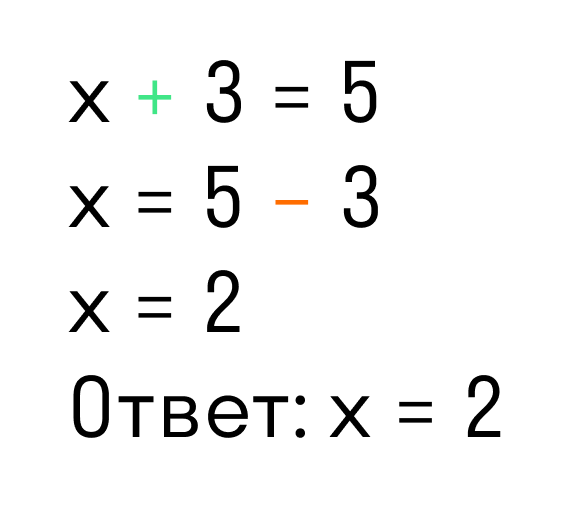Если a 0 и b 0 то линейное уравнение ax b

Если , то решением уравнения является любое число.

Если и , то уравнение корней не имеет.

Если , то уравнение называется линейным и имеет ровно одно решение

Корнем этого уравнения является число 1, поскольку при подстановке вместо этого числа получается верное числовое равенство.

Решите уравнение 0 ∙ + 1 = 0.

Имеем:

Это уравнение не имеет решений, поскольку ни при каких значениях переменной (которая, очевидно, явно не входит в уравнение) равенство не имеет место.

Ответ. Нет решений.

Решите уравнение 0 ∙ + 1 = 1.

Имеем

Решением этого уравнения является любое действительное число. В самом деле, при любом значении переменной равенство является верным.

Видео:Алгебра 7 Линейное уравнение с одной переменнойСкачать

Решение простых линейных уравнений

О чем эта статья:

Видео:Урок 7 ЛИНЕЙНОЕ УРАВНЕНИЕ С ОДНОЙ ПЕРЕМЕННОЙСкачать

Понятие уравнения

Уравнение — это математическое равенство, в котором неизвестна одна или несколько величин. Значение неизвестных нужно найти так, чтобы при их подстановке в пример получилось верное числовое равенство.

Например, возьмем выражение 2 + 4 = 6. При вычислении левой части получается верное числовое равенство, то есть 6 = 6.

Уравнением можно назвать выражение 2 + x = 6, с неизвестной переменной x, значение которой нужно найти. Результат должен быть таким, чтобы знак равенства был оправдан, и левая часть равнялась правой.

Корень уравнения — то самое число, которое при подстановке на место неизвестной уравнивает выражения справа и слева.

Решить уравнение значит найти все возможные корни или убедиться, что их нет.

Решить уравнение с двумя, тремя и более переменными — это два, три и более значения переменных, которые обращают данное выражение в верное числовое равенство.

Равносильные уравнения — это те, в которых совпадают множества решений. Другими словами, у них одни и те же корни.

Видео:Алгебра 7 класс. Линейное уравнение с одной переменной ax=b.Скачать

Какие бывают виды уравнений

Уравнения могут быть разными, самые часто встречающиеся — линейные и квадратные.

Особенность преобразований алгебраических уравнений в том, что в левой части должен остаться многочлен от неизвестных, а в правой — нуль.

Линейное уравнение выглядят так: ах + b = 0, где a и b — действительные числа. Вот, что поможет в решении:

если а ≠ 0 — уравнение имеет единственный корень: х = -b : а;

если а = 0 — уравнение корней не имеет;

если а и b равны нулю, то корнем уравнения является любое число.

Квадратное уравнение выглядит так: ax2 + bx + c = 0, где коэффициенты a, b и c — произвольные числа, a ≠ 0.

Числовой коэффициент — число, которое стоит при неизвестной переменной.

Кроме линейных и квадратных есть и другие виды уравнений, с которыми мы познакомимся в следующий раз:

Онлайн-курсы по математике за 7 класс помогут закрепить новые знания на практике с талантливым преподавателем.

Видео:Как решать уравнения? уравнение 7 класс. Линейное уравнениеСкачать

Как решать простые уравнения

Чтобы научиться решать простые линейные уравнения, нужно запомнить формулу и два основных правила.

1. Правило переноса. При переносе из одной части в другую, член уравнения меняет свой знак на противоположный.

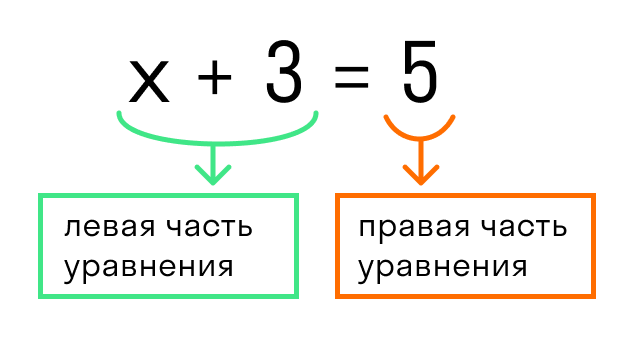
Для примера рассмотрим простейшее уравнение: x+3=5.

Начнем с того, что в каждом уравнении есть левая и правая часть.

Перенесем 3 из левой части в правую и меняем знак на противоположный.

Можно проверить: 2 + 3 = 5. Все верно. Корень равен 2.

Решим еще один пример: 6x = 5x + 10.

Перенесем 5x из правой части в левую. Знак меняем на противоположный, то есть на минус.

Приведем подобные и завершим решение.

2. Правило деления. В любом уравнении можно разделить левую и правую часть на одно и то же число. Это может ускорить процесс решения. Главное — быть внимательным, чтобы не допустить глупых ошибок.

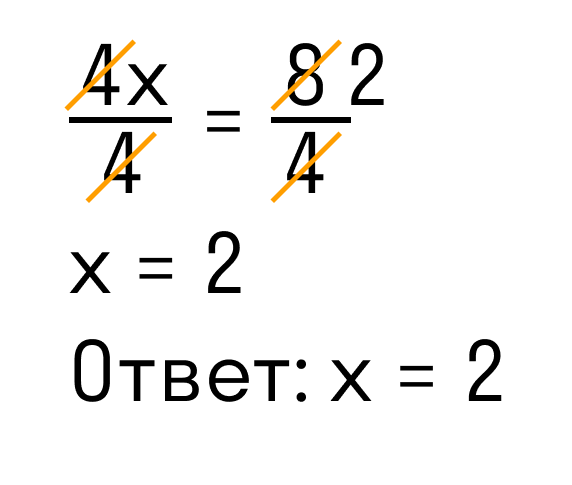
Применим правило при решении примера: 4x=8.

При неизвестной х стоит числовой коэффициент — 4. Их объединяет действие — умножение.

Чтобы решить уравнение, нужно сделать так, чтобы при неизвестной x стояла единица.

Разделим каждую часть на 4. Как это выглядит:

Теперь сократим дроби, которые у нас получились и завершим решение линейного уравнения:

Рассмотрим пример, когда неизвестная переменная стоит со знаком минус: -4x = 12

Разделим обе части на -4, чтобы коэффициент при неизвестной стал равен единице.

-4x = 12 | : (-4)
x = −3

Если знак минус стоит перед скобками, и по ходу вычислений его убрали — важно не забыть поменять знаки внутри скобок на противоположные. Этот простой факт позволит не допустить обидные ошибки, особенно в старших классах.

Напомним, что не у каждого линейного уравнения есть решение — иногда корней просто нет. Изредка среди корней может оказаться ноль — ничего страшного, это не значит, что ход решения оказался неправильным. Ноль — такое же число, как и остальные.

Способов решения линейных уравнений немного, нужно запомнить только один алгоритм, который будет эффективен для любой задачки.

Чтобы быстрее запомнить ход решения и формулу линейного уравнения, скачайте или распечатайте алгоритм — храните его в телефоне, учебнике или на рабочем столе.

Видео:Линейное уравнение с одной переменной. 6 класс.Скачать

Примеры линейных уравнений

Теперь мы знаем, как решать линейные уравнения. Осталось попрактиковаться на задачках, чтобы чувствовать себя увереннее на контрольных. Давайте решать вместе!

Пример 1. Как правильно решить уравнение: 6х + 1 = 19.

ЮПеренести 1 из левой части в правую со знаком минус.

Разделить обе части на множитель, стоящий перед переменной х, то есть на 6.

Пример 2. Как решить уравнение: 5(х − 3) + 2 = 3(х − 4) + 2х − 1.

5х − 15 + 2 = 3х − 12 + 2х − 1

Сгруппировать в левой части члены с неизвестными, а в правой — свободные члены. Не забываем при переносе из одной части уравнения в другую поменять знаки на противоположные у переносимых членов.

5х − 3х − 2х = −12 − 1 + 15 − 2

Приведем подобные члены.

Ответ: х — любое число.

Пример 3. Решить: 4х = 1/8.

Разделим обе части уравнения на множитель стоящий перед переменной х, то есть на 4.

Пример 4. Решить: 4(х + 2) = 6 − 7х.